随着经济社会的发展以及人们对身边美好水环境的向往,加之全国全面推行河长制,水环境治理受到人们越来越多的关注,投入力度也越来越大。但国内有关水环境综合整治效果评价的研究较少,类似研究多侧重于评价某一地区的河道或具体某条河流水体理化性质的改善。随着治理理论的逐步完善和治理实践的不断深入,评价方法从定性慢慢发展为定性定量相结合,单因素、单目标发展为多因素、多目标、多功能的综合评价[1]。建立一个能反映水环境综合治理效果的评价指标体系并给出合理可行的评价方法,将评价指标体系与评价方法有机地结合起来,才能系统全面地评价水环境综合治理效果,从而为巩固治水效果及今后的综合整治工作提供依据和指导[2]。
1 水环境综合治理效果评价指标体系 1.1 指标体系构建原则评价指标体系的构建主要遵循以下几个原则:①科学性原则。评价指标必须含义明确,具有一定的科学内涵,能够客观反映水环境综合治理效果评价指标体系内部结构关系;②可行性原则。水环境综合治理效果评价指标涉及面较广,应尽可能选择有代表性和可操作性的评价指标以便计算和分析;③层次性原则。评价指标应考虑到各个层次上的影响因素,能反映整个系统的主次关系;④全面性原则。指标体系应能相对全面和完整地反映水环境综合治理效果各个方面的影响;⑤动态性原则。水环境综合治理效果是变化的,指标体系需要全面反映时空维度的动态变化。
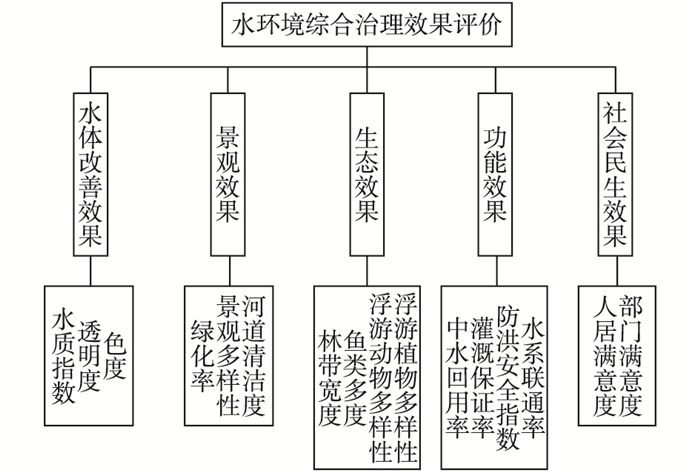
1.2 评价指标体系随着水环境治理实践的不断深入以及治理理论的完善,在水环境整治过程中不仅仅注重对河流本身的保护,在改善水质的基础上,同时注重河流功能性建设与生态修复,关注水环境生态系统自身健康及其可持续发展,实现多目标综合治理[3]。从水体改善效果、景观效果、生态效果、功能效果和社会民生效果5个方面选取了17项指标构建水环境治理效果评价指标体系,其指标体系如图 1。水环境综合治理的效果主要体现在水体改善,选取了水质指数、透明度和色度3个能直观反映水质变化的指标;水环境综合治理改变了自然景观和人文景观,选取绿化率、景观多样性和河道清洁度3个指标评价景观效果;选取了林带宽度、鱼类多度、浮游动物多样性和浮游植物多样性4个指标评价水环境综合治理对河岸带环境和生态环境的改善效果;水环境综合治理首先要确保河道的行洪安全,但单一的基本功能已经无法满足生活日益发展的需要,还需要增加其他功能以及可利用的方式保证水资源的充分利用,选择中水回用率、灌溉保证率、防洪安全指数和水系联通率4个指标评价功能效果;水环境综合治理应充分考虑对人类生活的影响,选取人居满意度和部门满意度2个指标评价对社会民生的效果。
|
图 1 水环境综合治理效果评价指标体系 Figure 1 Evaluation index system of comprehensive water environmental governance |
参照水质评价的相关国家标准及研究[4]、各指标的评价标准(河道生态健康评价指标研究[5])、综合国内研究成果[6-7]、咨询专家意见,对水环境综合治理效果进行评价等级划分,分为:优(0.7)、良(0.5)、中(0.3)、差(0.1)4个等级,具体见表 1。
| 表 1 水环境综合治理效果评价指标体系描述及分级 Table 1 Description and classification of evaluation index system of comprehensive water environmental governance |
AHP(层次分析法)是对存在相互联系和相互制约的多因素复杂事物进行分析的一种方法,通过层次的划分使之有序,并对每一层次因素的相对重要性进行对比,建立判断矩阵。通过计算判断矩阵的最大特征值以及对应的正交化特征向量,最终将系统确定为权值和措施优劣的排序[10-11]。AHP法权重确定的步骤如下:
(1) 评价指标两两比较构建判断矩阵,评价指标Ci和Cj两两比较得出相对重要数值aij,aji=1/aij,其具体数字及含义见表 2,通过比较得到判断矩阵A。
| $ \mathit{\boldsymbol{A}} = {({A_{ij}})_{n \times n}} $ |
| 表 2 指标相对重要度 Table 2 Relative importance of index |
(2) 计算特征向量,由式(1)进行归一化最终得到权重向量u1=(w1,w2,CR,wn)
| $ {w_i} = \frac{{{{(\prod\limits_{j = 1}^n {{a_{ij}}} )}^{1/n}}}}{{\sum\limits_{i = 1}^n {{{(\prod\limits_{j = 1}^n {{a_{ij}}} )}^{1/n}}} }}\left( {i, j = 1, 2, \ldots , n} \right) $ | (1) |
(3) 一致性检验,当ICR < 0.10时,则认为该判断矩阵的一致性是可以接受的,否则就需对判断矩阵的取值进行修正。
| $ {I_{{\rm{CI}}}} = \frac{{{\lambda _{{\rm{max}}}} - n}}{{n - 1}} $ | (2) |
| $ {I_{{\rm{CR}}}} = {I_{{\rm{CI}}}}/{I_{{\rm{RI}}}} $ | (3) |
式中:IRI为平均随机一致性指标,可通过查AHP法平均随机一致性指标取值表得到。
2.2 熵值法权重的确定熵值是对信息无序化的量度,熵值越大,则系统所蕴含的信息量就越小,系统某项属性的变异程度就越小;反之,系统的熵值越小,蕴含的信息量就越大,系统某项属性的变异程度就越大[12]。熵值法就是根据各项指标的观测值提供信息量的大小来确定指标的权重,某项属性的数据序列的变异程度越大,它相应的权重就越大。熵值法确定权重的步骤如下:
(1) 计算各个指标的熵值:
| $ {e_i} = \sum\limits_{j = 1}^m {{r_{ij}}{\rm{ln}}{r_{ij}}/{\rm{ln}}m} $ | (4) |
式中:
(2) 计算各指标的熵权wi,最后得到权重向量u2=(w1, w2, …, wn)。
| $ {w_j} = (1 - {e_j})/\sum\limits_{j = 1}^n {(1 - {e_j})} $ | (5) |
博弈论是分析决策主体行为相互影响时的理性行为及其决策均衡的问题,是研究具有竞争性事物的理论和方法[13-15]。博弈论组合赋权的基本思想是在不同权重之间寻找妥协或一致,最小化各个权重与最优权重之间的偏差,从而得到一个相对均衡和协调的组合权重向量[16]。
设有L种方法对指标赋权,则得到权重集uk=[uk1, uk2, …, ukn],其中:k=1, 2, …, L。记L个权重向量的任意组合为:
基于博弈论组合赋权的基本思想,优化的对策模型为:
| $ \left[ {\begin{array}{*{20}{c}} {{u_1} \cdot u_1^{\rm{T}}}&{{u_1} \cdot u_2^{\rm{T}}}& \cdots &{{u_1} \cdot u_L^{\rm{T}}}\\ {{u_2} \cdot u_1^{\rm{T}}}&{{u_2} \cdot u_2^{\rm{T}}}& \ldots &{{u_2} \cdot u_L^{\rm{T}}}\\ \cdots&\cdots&\cdots&\cdots \\ {{u_L} \cdot u_1^{\rm{T}}}&{{u_L} \cdot u_2^{\rm{T}}}& \cdots &{{u_L} \cdot u_L^{\rm{T}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{\alpha _1}}\\ {{\alpha _2}}\\ \cdots \\ {{\alpha _L}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{u_1} \cdot u_1^{\rm{T}}}\\ {{u_2} \cdot u_2^{\rm{T}}}\\ \cdots \\ {{u_L} \cdot u_L^{\rm{T}}} \end{array}} \right] $ | (6) |
计算得组合系数集{α1, α2, …, αL},对组合系数进行归一化处理:
为消除指标体系中各数据单位不同所造成的差异,需要对其归一化处理。为了便于归一化处理,将指标分为两类,一类是正向指标,即越大越优型;另一类是逆向指标,即越小越优型[17]。通过对数据的归一化处理,得到指标的归一化矩阵R=(rij)m×n。
| $ 正向指标:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {r_{ij}} = \frac{{{a_{ij}} - {\rm{mi}}{{\rm{n}}_j}({a_{ij}})}}{{{\rm{ma}}{{\rm{x}}_j}({a_{ij}}) - {\rm{mi}}{{\rm{n}}_j}({a_{ij}})}} $ | (7) |
| $ 逆向指标:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {r_{ij}} = \frac{{{\rm{ma}}{{\rm{x}}_j}({a_{ij}}) - {a_{ij}}}}{{{\rm{ma}}{{\rm{x}}_j}({a_{ij}}) - {\rm{mi}}{{\rm{n}}_j}({a_{ij}})}} $ | (8) |
式中:rij为归一化后的数据。
根据基于博弈论的组合权重法,计算得到综合权重u*=(w1,w2,w3,…,wn)T,建立线性加权水环境治理效果综合评价模型为:
| $ {P_i} = \sum\limits_{j = 1}^n {{r_{ij}}{w_j}} $ | (9) |
式中:i=1, 2, …, m。
4 实例研究宣城市为大力推进生态文明建设,围绕水安全、水生态、水管理、水环境、水文化等方面开展了水环境综合治理采取了控源截污、清淤疏浚、生态修复等一系列措施。指标数据来源于《宣城市统计年鉴》、《宣城市水资源公报》、水质监测报告和相关政府部门工作年报等,主观评价指标数据通过对宣城市水环境综合治理效果的1 000份问卷中得出,并广泛听取了专业人士的意见,具体数值见表 3。
| 表 3 宣城市水环境综合治理效果评价指标值 Table 3 Value of assessment index |
计算步骤:①计算指标的综合权重。根据上述AHP法的主观赋权,由专家对同一层次元素的相对重要性打分,筛选整合专家意见,运用Matlab编程,计算得到各指标的主观权重u1=(0.351 2,0.070 3,0.070 3,0.012 4,0.013 6,0.044 8,0.039 4,0.047 6,0.037 9,0.018 3,0.031 6,0.084 7,0.063 5,0.044 5,0.024 7,0.037 7,0.007 6);运用熵值法计算步骤得到客观权重u2=(0.099 5,0.074 1,0.076 6,0.060 4,0.062 8,0.060 9,0.049 8,0.049 3,0.049 3,0.049 3,0.037 7,0.037 2,0.036 9,0.037 7,0.037 1,0.100 4,0.081 1);可以看出两种方法得到的权重赋值有差异,基于得到的主观权重集和客观权重集{u1,u2},运用博弈论竞争与协调的关系式(6)计算组合系数,得到综合权重u=(0.364 1,0.070 1,0.069 9,0.009 9,0.011 1,0.044 0,0.038 8,0.047 5,0.037 3,0.016 7,0.031 3,0.087 1,0.064 9,0.044 9,0.024 0,0.034 5,0.003 8)。
② 指标归一化处理。依据式(7)、式(8)对数据进行归一化处理,具体结果见表 4。
| 表 4 归一化后的指标值 Table 4 Normalized assessment index |
③ 水环境综合治理效果评价。根据建立的水环境综合治理效果评价模型,将综合权重和归一化后的指标值代入式(9),得到宣城市2015—2017年水环境综合治理效果评价结果。
由评价结果可知,2015年宣城市水环境综合治理效果评价结果为0.529 2,等级为中;2016年评价结果为0.560 2,等级为良;2017年评价结果为0.620 8,等级为良,说明宣城市2015—2017年水环境综合治理取得了一定的效果。2016年和2017年评价等级都为良,但后者分值高于前者,说明在同一评价等级中,2017年的治理效果比2016年显著。从分值来看,2015—2017年综合评价得分呈逐渐增大的趋势,说明宣城市水环境综合治理效果在不断提高。
5 结语一直以来,我国缺少针对水环境综合治理效果的评价指标体系,结合科学性、可行性、层次性、全面性和动态性原则,构建了水环境综合治理效果评价指标体系,由AHP法确定主观权重,熵法确定客观权重,基于博弈论组合赋权建立了水环境综合治理效果评价模型,通过直观明确的得分值对水环境综合整治效果进行定量评价。通过结合实例研究,宣城市2015—2017年水环境治理效果等级为良或优,且治理效果逐年提高,证明了模型的可行性。水环境综合治理是一个长期的过程,该模型可在后续管理中为评价水环境综合治理效果以及科学制定水环境整治措施提供参考。
| [1] |
林积泉, 王伯铎, 马俊杰, 等. 小流域治理环境质量综合评价指标体系研究[J]. 水土保持研究, 2005, 12(1): 69-71. ( LIN Jiquan, WANG Boduo, MA Junjie, et al. Study on indicator system for environmental quality comprehensive assessment[J]. Research of Soil and Water Conservation, 2005, 12(1): 69-71. DOI:10.3969/j.issn.1005-3409.2005.01.020 (in Chinese)) |
| [2] |
程军蕊, 徐继荣, 郑琦宏, 等. 宁波市城区河道水环境综合整治效果评价方法及应用[J]. 长江流域资源与环境, 2015, 24(6): 1060-1066. ( CHENG Junrui, XU Jirong, ZHENG Qihong, et al. Evaluation method and application of comprehensive improvement of river water environment in Ningbo urban area[J]. Resources and Environment of the Yangtze River Basin, 2015, 24(6): 1060-1066. (in Chinese)) |
| [3] |
王俊敏. 水环境治理的国际比较及启示[J]. 世界经济与政治论坛, 2016(6): 161-170. ( WANG Junmin. International comparison and enlightenment of water environment governance[J]. World Economic and Political Forum, 2016(6): 161-170. DOI:10.3969/j.issn.1007-1369.2016.06.012 (in Chinese)) |
| [4] |
杨柳, 宋健飞, 宋波, 等. 主要污染物水质标识指数法在河流水质评价的应用[J]. 环境科学与技术, 2015, 38(11): 239-245. ( YANG Liu, SONG Jianfei, SONG Bo, et al. Application of main pollutant water quality identification index method in water quality evaluation[J]. Environmental Science and Technology, 2015, 38(11): 239-245. (in Chinese)) |
| [5] |
徐后涛.上海市中小河道生态健康评价体系构建及治理效果研究[D].上海: 上海海洋大学, 2016. (XU Houtao. Study on construction of ecosystem health evaluation system and governance effect of middle and small sized rivers in Shanghai[D]. Shanghai: Shanghai Ocean University, 2016. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10264-1016912177.htm
|
| [6] |
郑靓.兴城市头道沟小流域河道治理效果评价研究[D].长春: 东北师范大学, 2014. (ZHENG Liang. A study on evaluation of river regulation at Toudaogou in Xingcheng[D]. Changchun: Northeast Normal University, 2014. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10200-1014373575.htm
|
| [7] |
汪伦焰, 黄淑焕, 廉国伟, 等. 基于物元可拓模型对城市黑臭水体治理效果的评价[J]. 人民珠江, 2017, 38(10): 87-90. ( WANG Lunyan, HUANG Shuhuan, LIAN Guowei, et al. Effect evaluation of urban black-stink water treatment based on matter-element extension model[J]. Pearl River, 2017, 38(10): 87-90. DOI:10.3969/j.issn.1001-9235.2017.10.018 (in Chinese)) |
| [8] |
顾晓光, 白艳丽, 程锦. 塞氏盘法对水质透明度的测定[J]. 辽宁城乡环境科技, 2005(5): 21-22. ( GU Xiaoguang, BAI Yanli, CHENG Jin. Measurement of water transparency by means of secchi disc[J]. Liaoning Urban and Rural Environmental Science and Technology, 2005(5): 21-22. DOI:10.3969/j.issn.1674-1021.2005.05.009 (in Chinese)) |
| [9] |
顾春光. 重视林带的两个效益作用的发挥——谈林带宽度及其栽植密度[J]. 新疆林业, 1986(2): 17-20. ( GU Chunguang. Paying attention to the development of two benefits of forest belt—Talking about the width of forest belt and its planting density[J]. Forestry of Xinjiang, 1986(2): 17-20. (in Chinese)) |
| [10] |
李雪松, 孙博文. 基于层次分析的城市水环境治理综合效益评价——以武汉市为例[J]. 地域研究与开发, 2013, 32(4): 171-176. ( LI Xuesong, SUN Bowen. Evaluation of comprehensive benefits of urban water environment governance based on AHP—Taking Wuhan as an example[J]. Regional Research and Development, 2013, 32(4): 171-176. DOI:10.3969/j.issn.1003-2363.2013.04.033 (in Chinese)) |
| [11] |
李岱远, 高而坤, 吴永祥, 等. 基于网络层次分析法的节水型社会综合评价[J]. 水利水运工程学报, 2017(2): 29-37. ( LI Daiyuan, GAO Erkun, WU Yongxiang, et al. Comprehensive evaluation of water-saving society based on analytic network process[J]. Hydro-Science and Engineering, 2017(2): 29-37. (in Chinese)) |
| [12] |
高峰, 蔺欢欢, 邓红卫. 基于博弈论-模糊物元的地下水环境健康评价模型构建及应用[J]. 安全与环境学报, 2017, 17(4): 1543-1547. ( GAO Feng, LIN Huanhuan, DENG Hongwei. Construction and application of groundwater environmental health assessment model based on game theory and fuzzy matter element[J]. Journal of Safety and Environment, 2017, 17(4): 1543-1547. (in Chinese)) |
| [13] |
陈加良. 基于博弈论的组合赋权评价方法研究[J]. 福建电脑, 2003(9): 15-16. ( CHEN Jialiang. Based on game theory of combination weighting evaluation method[J]. Fujian Computer, 2003(9): 15-16. DOI:10.3969/j.issn.1673-2782.2003.09.009 (in Chinese)) |
| [14] |
任丽超, 栗振锋. 基于博弈论和模糊数学的桥梁风险评价模型[J]. 公路工程, 2017, 42(1): 163-169. ( REN Lichao, LI Zhenfeng. A new model based on the games theory and fuzzy mathematics in bridge engineering risk assessment[J]. Highway Engineering, 2017, 42(1): 163-169. DOI:10.3969/j.issn.1674-0610.2017.01.037 (in Chinese)) |
| [15] |
汪磊, 黄其松. 基于博弈论组合赋权的西部地区生态脆弱性评价[J]. 江苏农业科学, 2016, 44(3): 318-322. ( WANG Lei, HUANG Qisong. Assessment of ecological vulnerability in western region based on game theory combined weight method[J]. Jiangsu Agricultural Sciences, 2016, 44(3): 318-322. (in Chinese)) |
| [16] |
吴小萍, 储诚诚, 李月光, 等. 博弈论在高速公路施工期环境影响评价中的应用[J]. 郑州大学学报(工学版), 2012, 33(6): 36-40. ( WU Xiaoping, CHU Chengcheng, LI Yueguang, et al. Application of game theory in environmental impact assessment of expressway construction period[J]. Journal of Zhengzhou University(Engineering Edition), 2012, 33(6): 36-40. DOI:10.3969/j.issn.1671-6833.2012.06.009 (in Chinese)) |
| [17] |
孟颖, 唐德善, 石蓝星, 等. 基于改进指标体系的水资源调控方案评价模型[J]. 长江科学院院报, 2017, 34(5): 9-13. ( MENG Ying, TANG Deshan, SHI Lanxing, et al. Evaluation model of water resources regulation and control schemes based on improved index system[J]. Journal of Yangtze River Scientific Research Institute, 2017, 34(5): 9-13. (in Chinese)) |
 2018
2018 