2. 江苏省岩土工程技术工程研究中心,江苏 南京 210098;
3. 青岛市地铁一号线有限公司,山东 青岛 266000
土石坝具有抗震性能好、能够适应复杂地质条件、取材容易、经济效益好等优点,故而成为受青睐的坝型之一。目前,有多座300 m级土石坝在建或拟建,坝体变形的准确预测对合理设计大坝,保证其安全至关重要。土石坝的一个重要特征是蓄水后粗粒料会产生湿化变形,引起坝体应力应变状态变化。如果处理不当,会导致较为严重的后果,所以需要对粗粒料湿化变形进行深入研究。
目前,湿化变形计算方法和试验方法有“单线法”和“双线法”两种。Nobari等[1]提出用“双线法”进行湿化变形计算,分别对风干土和饱和土进行三轴试验,求出某一应力状态下这两种状态土的变形差,即为湿化变形量。魏松等[2]的研究表明单线法试验结果与实际更接近。因此,很多学者利用单线法研究土体湿化变形,得到了不少有价值的成果。沈珠江等[3-5]对比不同应力状态下的湿化变形试验后,认为应力水平较低时,湿化体积变形量可以近似为常数。李广信[6]提出了计算湿化变形的割线模型和塑性模型。李鹏等[7]的研究表明,湿化体积应变与应力水平呈反比例关系。魏松等[8-9]认为湿化体积应变随应力水平变化的关系主要受粗粒料干密度的影响。杜秦文等[10]认为密度和围压不仅影响湿化变形大小,还影响其发展规律。由于影响湿化变形的因素较多,已有成果不仅差别大,而且所建立的模型众多,所以目前尚无公认的合理可靠的规律及数学模型。因此,有必要对粗粒料湿化变形特性进行深入研究,以期建立与试验和实际情况相吻合的数学模型。
本文通过中三轴湿化试验对小浪底筑坝粗粒料进行研究,分析其湿化变形特性。基于三轴湿化变形试验结果,提出计算粗粒料湿化变形的数学模型,并给出模型参数的确定方法。
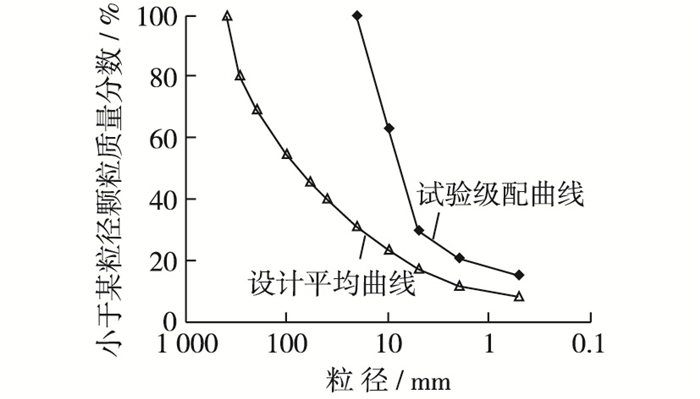
1 试验方案 1.1 试验材料试验用料为小浪底斜心墙堆石坝的筑坝粗粒料,母岩为褐色砂岩。由于三轴试样的直径仅101 mm,因此根据土工试验规程[11]采用混合法对粗粒料原始级配进行缩尺,缩尺后试验用料的最大粒径为20 mm,缩尺前后的级配曲线见图 1。试验制样干密度为1.98 g/cm3,相对密度为0.85。
|
图 1 试样级配曲线 Figure 1 Particle size distribution curves |
采用单线法进行试验,三轴湿化变形试验的试样直径为101 mm,高为200 mm。试样由风干土料制备,完成后将干样按应变控制剪切至一定应力状态,保持应力不变,待试样变形稳定,用1 m常水头从试样底部加水湿化使试样饱和。湿化完成后,继续剪切至峰值。
共进行了9组湿化变形试验,对应3个围压即300, 600和900 kPa,每个围压对应3个不同的应力水平0.25,0.50和0.75(以下称为湿化应力水平)。这里,湿化应力水平定义为试样处于饱和状态下,相同围压时,当前偏应力与破坏偏应力之比,即s=(σ1-σ3)/(σ1-σ3)f。
2 试验结果及分析给出围压σ3=600 kPa时,不同湿化应力水平下的湿化轴向应变与偏应力关系曲线和轴向应变与体积应变关系曲线,见图 2。本文只研究湿化变形,不研究湿化前后强度变化,故湿化完成后剪切至峰值的曲线不再给出。

|
图 2 湿化变形应力应变关系曲线 Figure 2 Relationship between stress and strain in wetting tests |
围压为300和900 kPa下的湿化应力应变曲线与此类似,不再给出。图 2(a)中每条曲线末端都有1段近似水平的直线,直线上箭头所标示的位置分别为湿化开始点和湿化结束点,中间直线段对应的就是湿化过程产生的轴向应变量,记为Δε1w。同样的,图 2(b)中,每条曲线左边箭头所示位置为湿化起点,右边箭头为湿化结束点,箭头之间的体积应变差即为湿化体积应变量,记为Δεvw。
依据试验结果整理出湿化轴向应变量和湿化体积应变量。图 3(a)给出试样在不同围压σ3下对应的湿化轴向应变Δε1w随湿化应力水平s的变化规律。图 3(a)表明,在相同围压下,湿化应力水平越高湿化轴向应变越大,可以近似认为呈双曲线关系。张少宏等[12]通过试验研究也得到过类似结论。该双曲线与Δε1w轴交点的物理意义是等压条件下的湿化轴向应变Δε1w, 0。为分析Δε1w随σ3的变化关系,点绘出了不同应力水平下Δε1w与σ3之间的关系,如图 3(b)所示。可以看出,在相同湿化应力水平下,σ3越高,Δε1w越大,近似呈线性增长。

|
图 3 湿化轴向应变变化规律 Figure 3 Variation of wetting axial strain |
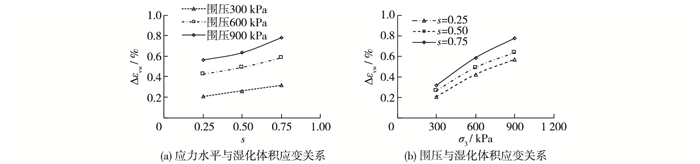
图 4(a)给出试样在不同围压σ3和不同湿化应力水平下对应的湿化体积应变Δεvw变化规律。可以看出,在相同围压下,湿化应力水平越高,湿化体积应变越大,它们之间近似呈线性关系。彭凯等[13]的试验研究也有类似发现。该直线与Δεvw轴交点的物理意义是等压条件下的湿化体积应变Δεvw, 0。从图 4(b)可以看出,在相同湿化应力水平下,围压越高,湿化体积应变越大,而且,也近似呈线性增长。
|
图 4 湿化变形应力应变体变关系曲线 Figure 4 Variation of wetting volumetric strain |
根据上述分析,假定图 3(a)的湿化变形轴向应变与湿化应力水平的关系曲线可以用双曲线拟合,即Δε1w-s关系可以用式(1)表示:
| $ \Delta {{\varepsilon }_{\text{1w}}}=\frac{as}{1-bs}+\Delta {{\varepsilon }_{\text{1w,0}}} $ | (1) |
式中:Δε1w, 0为各向等压条件下的湿化轴向应变;a,b为拟合参数。
式(1)可以写成另一种形式:
| $ s=\frac{1}{\frac{a}{\left( \Delta {{\varepsilon }_{\text{1w}}}-\Delta {{\varepsilon }_{\text{1w,0}}} \right)}+b} $ | (2) |
将式(2)中湿化轴向应变差取极限趋于无穷,则有:
| $ \mathop {\lim }\limits_{\left( {\Delta {\varepsilon _{{\rm{1w}}}} - \Delta {\varepsilon _{{\rm{1w,0}}}}} \right) \to \infty } {\mkern 1mu} s = \frac{1}{b} $ | (3) |
按照s的定义,其最大值为1。因此,式(3)中s的极限值应该等于1,故有b=1。这里也可以看出,如果应力水平趋于1,意味着湿化应变趋于无限,或者说,当应力水平较大时,式(1)计算得的湿化轴向应变会很大,这与目前的试验成果不一致。因此,式(1)不适用于很高应力水平下的湿化变形计算。这里,可初步认定该模型在湿化应力水平s≤0.75的情况下适用。
将式(1)中的湿化轴向应变差(Δε1w-Δε1w, 0)对s求导:
| $ \frac{\text{d}\left( \Delta {{\varepsilon }_{\text{1w}}}-\Delta {{\varepsilon }_{\text{1w,0}}} \right)}{\text{d}s}=\frac{a}{{{\left( 1-bs \right)}^{2}}} $ | (4) |
当湿化应力水平s趋于0时:
| $ \mathop {\lim }\limits_{s \to 0} {\mkern 1mu} \frac{{{\rm{d}}\left( {\Delta {\varepsilon _{{\rm{1w}}}} - \Delta {\varepsilon _{{\rm{1w,0}}}}} \right)}}{{{\rm{d}}s}} = a $ | (5) |
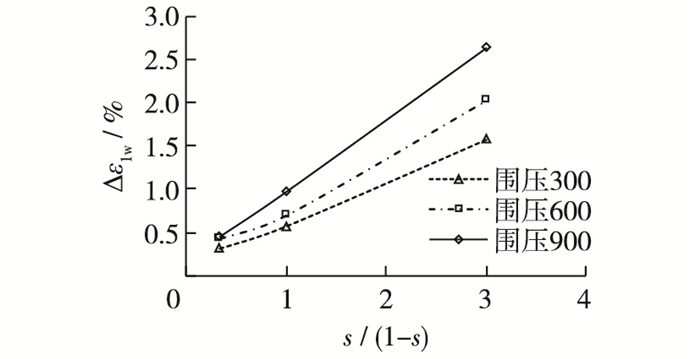
由式(5)可见,参数a的物理意义是图 3(a)中的双曲线初始斜率(对应s=0)。绘出Δε1w与s/(1-s)的关系曲线,如图 5所示。可以看出Δε1w与s/(1-s)呈线性关系,联系式(1)可得参数a是图 5中各直线的斜率。
|
图 5 湿化轴向应变与s/(1-s)的关系 Figure 5 Relationship between wetting axial strain and s/(1-s) |
由图 5还可看出,拟合直线的斜率a随围压σ3的不同而不同。因此,绘出参数a与对应围压σ3之间的关系曲线,如图 6所示。可以看出参数a与围压σ3呈线性关系。

|
图 6 参数a随围压σ3的变化情况 Figure 6 Relationship between parameter a and confining pressure |
故参数a可用下式表示:
| $ a={{K}_{1}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+A $ | (6) |
式中:K1,A分别为直线的斜率和截距;Pa为大气压。
如图 3(b)所示,湿化轴向应变与围压在相同湿化应力水平下近似呈线性关系。因此,可假定在各向等压即湿化应力水平为零时,轴向应变Δε1w, 0与围压σ3呈线性关系:
| $ \Delta {{\varepsilon }_{\text{1w,0}}}={{K}_{0}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+{{A}_{0}} $ | (7) |
式中:K0为材料参数。
将式(6)和式(7)代入式(1)得湿化轴向应变:
| $ \Delta {{\varepsilon }_{\text{1w}}}=\frac{\left[ {{K}_{1}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+A \right]s}{1-s}+{{K}_{0}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+{{A}_{0}} $ | (8) |
由式(8)可以看出,湿化轴向应变与湿化应力水平呈双曲线关系,与围压呈线性关系,与图 3变化规律相符。
3.2 湿化体积应变根据上述试验结果的分析,假定图 4(a)的湿化变形体积应变与湿化应力水平的关系曲线可以用直线拟合,故可以用式(9)表示:
| $ \Delta {{\varepsilon }_{\text{vw}}}={{K}_{\text{v}}}s+\Delta {{\varepsilon }_{\text{vw,0}}} $ | (9) |
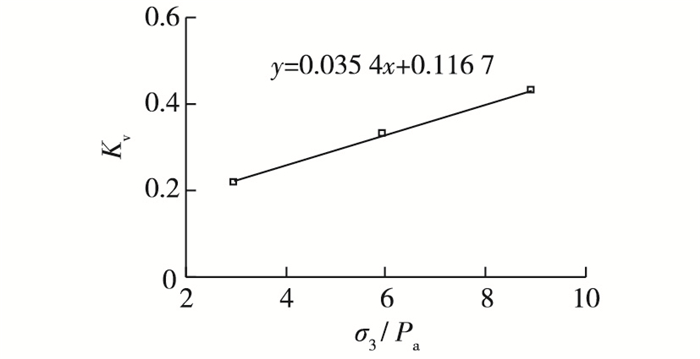
式中:Kv,Δεvw, 0分别为拟合直线的斜率和截距。图 4(a)表明Kv是关于围压σ3的函数。因此,根据图 4(a)拟合曲线斜率,整理出Kv与围压σ3关系,如图 7所示。可以看出,两者有良好的线性关系,故Kv可表示为:
| $ {{K}_{\text{v}}}={{K}_{2}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+B $ | (10) |
|
图 7 Kv随围压σ3变化关系 Figure 7 Relationship between parameter Kv and confining pressure |
式中:K2,B分别为直线的斜率和截距。
式(9)中,Δεvw, 0为各向等压时(s=0)的湿化体积应变。魏松等发现当湿化应力水平为0时,湿化体积应变与湿化轴向应变的比值在3左右,且不随围压大小变化,故可假定Δεvw, 0=3Δε1w, 0。即当湿化应力水平为零时,可假定土体是各向同性材料,则由式(7)可以得到:
| $ \Delta {{\varepsilon }_{\text{vw,0}}}=3\Delta {{\varepsilon }_{\text{1w,0}}}=3\left[ {{K}_{0}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+{{A}_{0}} \right] $ | (11) |
将式(10)和式(11)代入式(9)得湿化体积应变为:
| $ \Delta {{\varepsilon }_{\text{vw}}}=\left[ {{K}_{2}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+B \right]s+3\left[ {{K}_{0}}\left( \frac{{{\sigma }_{3}}}{{{P}_{\text{a}}}} \right)+{{A}_{0}} \right] $ | (12) |
由式(12)可以看出,湿化体积应变与湿化应力水平和围压都呈线性关系,与图 4变化规律相符。
式(8)和式(12)即是本文提出的湿化变形模型。由此模型,即可计算应力状态小于0.75时的湿化轴向应变和湿化体积应变。
3.3 参数确定方法本文提出的湿化变形计算模型中涉及的材料参数有:K0, A0, K1, A, K2和B,其确定方法概括如下:
(1) 通过单线法三轴湿化变形试验(3~4个围压,每个围压3~4个应力水平),测得湿化轴向应变和湿化体积应变。分别点绘出湿化轴向应变与湿化应力水平、湿化轴向应变与围压、湿化体积应变与湿化应力水平、湿化体积应变与围压的关系曲线。
(2) 对于每一个σ3,都可以得到一个各向等压湿化轴向应变Δε1w,0,点绘出Δε1w,0-σ3/Pa的关系曲线,近似为直线,斜率为参数K0,截距为A0。
(3) 当围压一定时,Δε1w与s/(1-s)是线性关系,其直线斜率为湿化轴向应变与湿化应力水平关系曲线的初始斜率,由此点绘出a-σ3/Pa的关系曲线,近似取为直线,斜率为K1,截距为A。
(4) 将湿化体积应变与湿化应力水平关系曲线视为直线,并计算各条直线的斜率Kv,点绘出Kv-σ3/Pa的关系,用直线拟合,其斜率为K2,截距为B。
4 模型验证选取本文试验数据300,600和900 kPa共3个围压,0.25,0.50,0.75共3个应力水平下的湿化轴向应变以及湿化体积应变的试验数据。选取文献[14]中800,1 600,2 400 kPa共3个围压,0,0.2,0.4,0.6,0.8共5个应力水平下的花岗岩粗粒料湿化轴向应变以及湿化体积应变的试验数据。用本文模型计算出湿化轴向应变与湿化体积应变,并与文献和本文试验数据进行对比,验证模型的可靠性。整理出的模型参数列于表 1。
| 表 1 模型参数 Table 1 Parameters of proposed model |
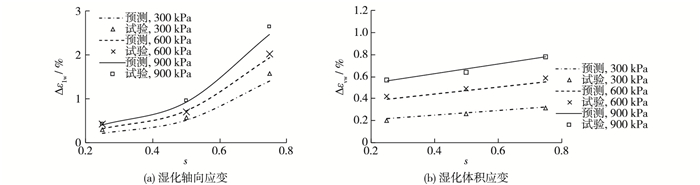
将围压为300,600,900 kPa时的模型计算曲线与本文试验结果曲线作对比,见图 8。本文模型计算湿化轴向应变和湿化体积应变都与试验结果吻合很好。
|
图 8 本文试验数据与模型验证结果比较 Figure 8 Comparison between simulated results by proposed model and test results |
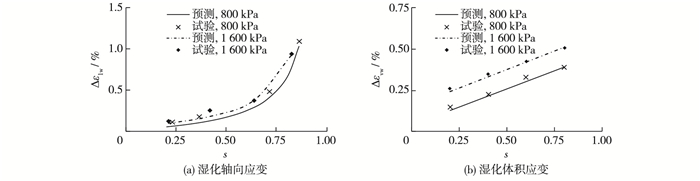
将围压为800和1 600 kPa时的模型计算曲线与程展林试验结果[14]曲线作对比,见图 9。本文模型计算湿化轴向应变和湿化体积应变都与试验结果吻合很好。
|
图 9 本文模型与程展林[14]试验结果比较 Figure 9 Comparison between simulated results by proposed model and Cheng Zhanlin's test results[14] |
通过上述比较可以看出,本文湿化变形模型能够较好地反映不同粗粒料的湿化变形特性,可以应用于实际工程中粗粒料的湿化变形预测。
5 结语本文对小浪底土石坝砂岩粗粒料进行了三轴湿化变形试验,对粗粒料湿化变形特性进行了分析。根据试验结果总结出基于单线法的湿化变形计算模型,并得到以下结论:
(1) 粗粒料湿化轴向应变和体积应变随湿化应力水平增加而增加,湿化轴向应变和湿化应力水平呈双曲线关系,体积应变与湿化应力水平呈线性关系。
(2) 粗粒料湿化轴向应变和体积应变随围压增加而增加,且均近似呈线性关系。
(3) 本文提出的湿化变形模型,充分考虑了围压和湿化应力水平的影响,能很好地反应湿化变形的特性。模型中6个参数的意义明确,确定方法简单。
(4) 验证表明,本文提出的模型预测曲线与两组试验结果吻合程度较高,证明该模型有较好的可靠性,可用于粗粒料湿化变形计算。
| [1] |
NOBARI E S, DUNCAN J M. Movements in dams due to reservoir filling[C]//Performance of Earth and Earth Supported Structures, Vol1, Part1, 1973.
|
| [2] |
魏松, 朱俊高. 粗粒土料湿化变形三轴试验研究[J]. 岩土力学, 2007(8): 1609-1614. ( WEI Song, ZHU Jungao. Study on wetting behavior of coarse grained soil in triaxial test[J]. Rock and Soil Mechanics, 2007(8): 1609-1614. DOI:10.3969/j.issn.1000-7598.2007.08.015 (in Chinese)) |
| [3] |
左元明, 沈珠江. 坝壳砂砾料浸水变形特性的测定[J]. 水利水运科学研究, 1989(1): 108-113. ( ZUO Yuanming, SHEN Zhujiang. Determination of deformation character of gravel sand due to wetting[J]. Journal of Nanjing Hydraulic Research Institute, 1989(1): 108-113. (in Chinese)) |
| [4] |
朱百里, 沈珠江. 计算土力学[M]. 上海: 上海科学技术出版社, 1990. ( ZHU Baili, SHEN Zhujiang. Calculation of soil mechanics[M]. Shanghai: Shanghai Science and Technology Press, 1990. (in Chinese))
|
| [5] |
沈珠江, 王剑平. 土质心墙坝填筑及蓄水变形的数值模拟[J]. 水利水运科学研究, 1988(4): 47-64. ( SHEN Zhujiang, WANG Jianping. Numerical simulation of construction behavior of clay core dam and its movement due to reservoir impounding[J]. Journal of Nanjing Hydraulic Research Institute, 1988(4): 47-64. (in Chinese)) |
| [6] |
李广信. 堆石料的湿化试验和数学模型[J]. 岩土工程学报, 1990, 12(5): 58-64. ( LI Guangxin. Study on wetting of rock fill[J]. Chinese Journal of Geotechnical Engineering, 1990, 12(5): 58-64. DOI:10.3321/j.issn:1000-4548.1990.05.007 (in Chinese)) |
| [7] |
李鹏, 李金, 刘金禹. 粗粒料的大型高压三轴湿化试验研究[J]. 岩石力学与工程学报, 2004, 23(2): 231-234. ( LI Peng, LI Jin, LIU Jinyu. Slaking test study of coarse aggregate under high triaxial stress condition[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(2): 231-234. DOI:10.3321/j.issn:1000-6915.2004.02.011 (in Chinese)) |
| [8] |
魏松, 朱俊高. 粗粒料湿化变形三轴试验中的几个问题[J]. 水利水运工程学报, 2006(1): 19-23. ( WEI Song, ZHU Jungao. Discussion on some problems in triaxial wetting test of coarse-grained materials[J]. Hydro-Science and Engineering, 2006(1): 19-23. DOI:10.3969/j.issn.1009-640X.2006.01.004 (in Chinese)) |
| [9] |
魏松, 朱俊高. 粗粒料三轴湿化颗粒破碎试验研究[J]. 岩石力学与工程学报, 2006, 25(6): 1252-1258. ( WEI Song, ZHU Jungao. Study on wetting breakage of coarse-grained materials in triaxial test[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(6): 1252-1258. DOI:10.3321/j.issn:1000-6915.2006.06.025 (in Chinese)) |
| [10] |
杜秦文, 刘永军, 曹周阳. 变质软岩路堤填料湿化变形规律研究[J]. 岩土力学, 2015, 36(1): 41-46. ( DU Qinwen, LIU Yongjun, CAO Zhouyang. Large-scale triaxial tests on metamorphic soft rock embankment filler for wetting deformation characteristics[J]. Rock and Soil Mechanics, 2015, 36(1): 41-46. (in Chinese)) |
| [11] |
SL237—1999土工试验规程[S]. (SL237—1999 Specification of soil test[S]. (in Chinese))
|
| [12] |
张少宏, 张爱军, 陈涛. 堆石料三轴湿化变形特性试验研究[J]. 岩石力学与工程学报, 2005, 增刊2: 5938-5942. ( ZHANG Shaohong, ZHANG Aijun, CHEN Tao. Triaxial slacking test research on rock fill deformation feature[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 增刊2(Suppl2): 5938-5942. (in Chinese)) |
| [13] |
彭凯, 朱俊高, 王观琪. 堆石料湿化变形三轴试验研究[J]. 中南大学学报(自然科学版), 2010, 41(5): 1953-1960. ( PENG Kai, ZHU Jungao, WANG Guanqi. Study on slaking deformation of rockfill materials by triaxial test[J]. Journal of Central South University (Science and Technology), 2010, 41(5): 1953-1960. (in Chinese)) |
| [14] |
程展林, 左永振, 丁红顺, 等. 堆石料湿化特性试验研究[J]. 岩土工程学报, 2010, 32(2): 243-247. ( CHENG Zhanlin, ZUO Yongzhen, DING Hongshun, et al. Wetting characteristics of coarse-grained materials[J]. Chinese Journal of Geotechnical Engineering, 2010, 32(2): 243-247. (in Chinese)) |
2. Jiangsu Research Center for Geotechnical Engineering Technology, Hohai University, Nanjing 210098, China;
3. Qingdao Metro Line 1 Co., Ltd., Qingdao 266000, China
 2018
2018 
