水库浸没是由于水库蓄水或其他人类工程活动,导致地下水水位上升,引起环境地质灾害的一种现象[1]。水库浸没研究通常采用解析法或数值模拟法对研究区地下水渗流进行计算分析[2],进而预测研究区浸没范围、浸没程度和控制浸没的效果。19世纪60年代到20世纪末,解析法是定量模拟计算地下水渗流问题最有效的方法[3],但由于解析法大多基于简化边界条件下的地下水稳定流问题,不能精确刻画复杂水文地质条件下的地下水渗流场动态变化。自20世纪末期以来,得到飞速发展的数值模拟法克服了解析法计算的局限性[4],已广泛应用于计算、分析、评价地下水渗流场问题以及渗流机理研究,也是水库浸没研究最有效的方法,成熟的商业软件为地下水渗流场的精确计算模拟提供了重要的方法和研究基础。Gleeson等[5]采用数值方法模拟了山区地下水渗流场;Doble等[6]建立地下水非稳定模型研究了洪水对漫滩浅层地下水渗流的影响;Scibek[7]采用数值模拟法量化气候对地下水渗流的影响;骆祖江等[8]采用数值模型预测了水库蓄水后的不同防渗方案对水库渗漏量影响。
水库浸没控制一般通过工程措施实现,工程控制措施主要有防渗墙和减压井[9],许多学者对其控制效果进行了深入研究。王晓燕等[10]通过对比不同悬挂式防渗墙深度下围堰下游出溢处的渗流坡降,找到最优防渗方案;冶雪艳等[11]研究了不同防渗墙长度对库区地下水渗流的影响,确定最优渗控方案;吕路等[12]通过数值模拟,研究不同防渗墙深度对人工湖周围浅层地下水渗流的影响,选取最优防渗方案;骆祖江等[13]深入研究了设置到潜水含水层且不同长度的防渗墙对库区左岸浸没的影响;曹洪等[14]分析了减压井间距和出水口高程不同对库区地下水渗流场的影响,选取最优防渗方案。
目前,已有许多学者对水库浸没及其控制措施进行了深入研究,但类似江心洲浸没问题的研究却很少。本文以新干航电枢纽工程江心洲为例,采用数值模拟的方法结合垂直防渗墙和减压井优化控制浸没问题,考虑到多年平均水文条件,按堤外抬田防渗和堤内多种浸没控制措施(防渗墙与减压井联合布设工况方案)进行江心洲浸没模拟预测与控制。
1 工程区概况江西赣江新干航电枢纽工程位于江西省吉安市新干县域内的赣江中游末段,正常蓄水位为32.5 m,回水长度56 km,总库容5亿m3,集水面积64 776 km2,坝址处多年平均径流量为533亿m3,多年平均流量为1 690 m3/s,主要建筑级别为3级,次要建筑物为4级,是以航运为主、兼顾发电等综合效益的二等工程。江心洲位于坝址上游8.6 km处,天然条件下江心洲地下水埋深较浅,库区蓄水后,边界条件发生改变,地下水位相应抬高至接近地表,可能发生浸没问题,影响洲上居民生活和生态休闲旅游区的建设,因此江心洲浸没评价和防治方案的研究具有十分重要的意义。
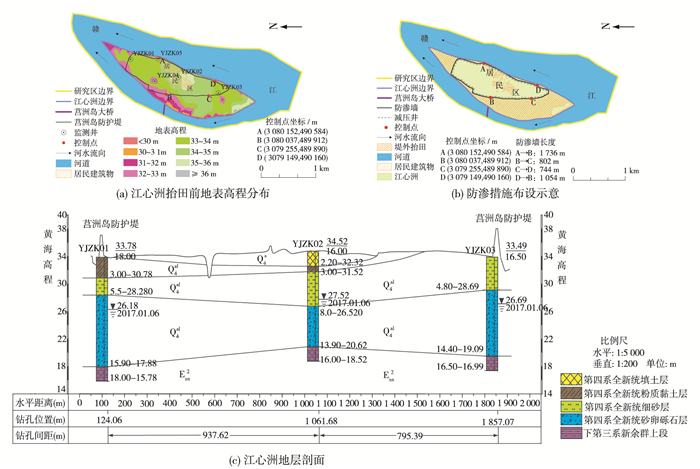
研究区总面积5.05 km2,其中陆地占31.57%,河道占比68.43%。江心洲地势平坦低洼,高程在31.54~36.10 m,南部高程高,北部较低,如图 1(a)所示。江心洲上建有莒洲岛防护堤,如图 1(b),堤脚后18 m处有居民建筑物。研究区地层上覆第四系全新统(Q4)松散沉积物,下伏第三系新余群上段(Exn2)红层,人工堆积层(Q4s)和河流冲积层(Q4al)构成江心洲第四系全新统地层,如图 1(c)所示。第四系全新统地层在莒洲岛大桥以北为典型二元结构,上层为壤土和粉质黏土,厚约4.5 m,并在莒洲岛大桥处尖灭,下层上部是厚约2.6 m的细砂层,下接6~10 m厚的砂卵砾石层;在莒洲岛大桥以南为一元结构,直接出露厚度均匀的细砂层,厚约5 m,下接6~10 m厚的砂卵砾石;围绕江心洲的U型河谷直接切穿到砂卵砾石层。
|
图 1 江心洲抬田前地表高程分布、防渗措施布设及地层剖面 Figure 1 Topographic distribution without immersion control measures, anti-immersion measures and strata profile of mid-channel bar |
江心洲地下水主要为第四系松散沉积物孔隙水,接受大气降水补给。赣江是区内最大地表水体,自南向北流经研究区,天然条件下,枯水期地下水位略高于赣江水位,地下水补给赣江,丰水期赣江水位略高于地下水位,赣江补给地下水。地下水部分以蒸发、植被蒸腾以及村镇居民以散点井形式分散开采的方式消耗。
2 研究区数值模型 2.1 研究区水文地质概念模型研究区以赣江江水位为界,形成了一个具有统一渗流场的完整水文地质单元。模型中壤土层、粉质黏土层和莒洲岛大桥以南的砂层为潜水含水层,莒洲岛大桥以北的砂层和研究区砂卵砾石层为承压含水层,基岩岩性完整且导水性差为相对隔水层。围绕江心洲的赣江为第一类边界,莒洲岛大桥以南地下水自由面边界主要埋藏在砂层中,莒洲岛大桥以北地下水自由面边界埋藏在壤土及粉质黏土层中,松散沉积物下部的基岩面为研究区底部隔水边界。库区蓄水后,由于通航需求,库水位需长期保持在32.5 m,相应研究区的地下水位随着库水位的抬升也将发生持续抬升,水库达到正常蓄水高程后,莒洲岛大桥以北粉质黏土层将变为承压含水层。
2.2 数学模型根据上述水文地质概念模型,得出研究区为非均质介质中地下水流系统三维非稳定数学模型:
| $ \left\{ \begin{array}{l} \frac{\partial }{{\partial x}}\left( {K\frac{{\partial H}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {K\frac{{\partial H}}{{\partial y}}} \right)\frac{\partial }{{\partial z}}\left( {K\frac{{\partial H}}{{\partial z}}} \right) + W = {\mu _{\rm{S}}}\frac{{\partial H}}{{\partial t}}\;\;\;\;\left( {x, y, z \in \mathit{\Omega }, t \ge 0} \right)\\ \frac{\partial }{{\partial x}}\left( {K\frac{{\partial H}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {K\frac{{\partial H}}{{\partial y}}} \right)\frac{\partial }{{\partial z}}\left( {K\frac{{\partial H}}{{\partial z}}} \right) + \varepsilon = \mu \frac{{\partial H}}{{\partial t}}\;\;\;\;\;\;\;\;\left( {x, y, z \in {\mathit{\Gamma }_3}, t \ge 0} \right)\\ H\left( {x, {\rm{ }}y, {\rm{ }}z, {\rm{ }}t} \right)\left| {_{t = 0}} \right. = {H_0}(x, {\rm{ }}y, {\rm{ }}z, {\rm{ }}{t_0})\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x, {\rm{ }}y, {\rm{ }}z \in \mathit{\Omega }} \right)\\ H\left( {x, {\rm{ }}y, {\rm{ }}z, {\rm{ }}t} \right)\left| {_{{\mathit{\Gamma }_1}}} \right. = {H_0}(x, {\rm{ }}y, {\rm{ }}z, {\rm{ }}t)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x, {\rm{ }}y, {\rm{ }}z \in {\mathit{\Gamma }_1}} \right)\\ \partial H/\partial n\left| {_{{\mathit{\Gamma }_2}} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x, {\rm{ }}y, {\rm{ }}z \in {\mathit{\Gamma }_2}} \right)} \right.\\ H\left( {x, {\rm{ }}y, {\rm{ }}z, {\rm{ }}t} \right)\left| {_{{\mathit{\Gamma }_3}} = z\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {x, {\rm{ }}y, {\rm{ }}z \in {\mathit{\Gamma }_2}} \right)} \right. \end{array} \right. $ | (1) |
式中:Ω为渗流区域;K为渗透系数(m/d);H为水位(m);μS为贮水率(1/m);μ为饱和差或给水度;W为单位时间从单位体积含水层流入或流出的水量(1/d);ε为单位时间在垂向上从单位面积含水层自由面流入或流出的水量(m/d);H0为初始水位(m);H1为第一类边界水位(m);n为隔水边界的法线方向;x,y,z为空间位置;Γ1为第一类边界;Γ2为第二类边界(隔水边界);Γ3为自由面边界。
2.3 模型识别与验证模型平面上共剖分为74 792个单元,最小三角形边长1.37 m,如图 2(a)所示。根据新干水文站监测水位,按左、右河道水力坡度0.21‰和0.28‰,插值得到赣江天然水位。根据地形地貌、地层岩性,将整个模型分为15个参数区,如图 2(b),其中砂卵砾石及粉质黏土渗透系数、砂卵砾石贮水率初始值由野外现场抽水试验和振荡试验得到,其余相关参数初始值由相关规范获得[15],设置的地下水净补给系数为地下水净补给量与降水量的比值,其中地下水净补给量参考文献,降水量在吉安市水文信息服务系统上获取。

|
图 2 研究区模型剖分与参数分区 Figure 2 Model partition and parameter partitioning in the study area |
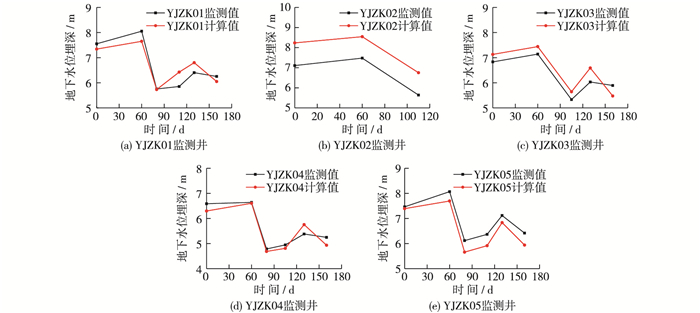
选择初次实测水位时间作为模型识别率定时间,在给定模型边界条件及地下水净补给量的基础上,反复调试水文地质参数,最终钻孔水位计算值与实测值拟合结果较好。模型识别后的地下水渗流场可作为模型验证的初始条件,在赋予模型2017年1—6月份的边界条件和地下水净补给量下,进行模型非稳定流计算,时间步长5 d,采用动态监测水位对模型进行校正。在模型识别基础上,微调水文地质参数,使得计算值与实测值能较好拟合。拟合结果如图 3所示,各期监测井计算值有86.77%在0.5 m置信区间内,平均误差为0.11 m。模型拟合结果表明,模型能够良好地展现天然地下水形态,可以用来进行江心洲浸没和控制方案的预测,此时各地层的水文地质参数见表 1。
|
图 3 各监测井承压水位埋深计算值与实测值拟合 Figure 3 Fitting of calculated and measured confined water levels below surface in observation wells |
| 表 1 研究区各地层水文地质参数 Table 1 Hydrogeological parameters of various layers in study area |
江心洲部分表层土为二元结构上部的细颗粒的壤土及粉质黏土,部分表层土为一元结构的细砂,用地下水位临界埋深来判定浸没标准时,不能忽略土壤毛细管水上升高度。由于江心洲堤内区域建有民舍,堤内外浸没标准不同。地下水位埋深小于0.6 m时,不宜农田农作,堤内外均为严重浸没;地下水位埋深0.6~2.1 m,土地可耕作、不宜建造民舍,堤内划分为中度浸没,堤外为轻度浸没;地下水位埋深2.1~2.6 m,民舍地基稳定性差,堤内划分为轻度浸没区,堤外未浸没;地下水位埋深大于等于2.6 m,堤内及堤外均未发生浸没。
江心洲浸没控制主要考虑抬田(抬田区为堤外,如图 1(b),高程为34.6 m)、防渗墙、减压井3种措施,具体工况为无防渗,堤外抬田,堤外抬田及堤内防渗墙不同长度、深度,堤外抬田及堤内减压井井径、井列线[17]位于堤脚后不同距离,堤外抬田及堤内减压井及不同长度防渗墙共14种工况,具体工况安排见表 2,其中防渗墙为垂直截渗墙,渗透系数为6.68×10-5 m/d,并建立在莒州岛防护堤上;减压井均为深入承压含水层底部的完整井,莒州岛大桥以南减压井井间距为29 m,莒州岛大桥以北井间距为13 m。各工况以2018-01-01为初始时刻进行10年预测。预测结果见表 3。
| 表 2 防渗措施布设情况 Table 2 Arrangements of anti-immersion measures in study area |
| 表 3 各工况下江心洲浸没面积统计 Table 3 Statistics of immersed area in mid-channel bar under different conditions |
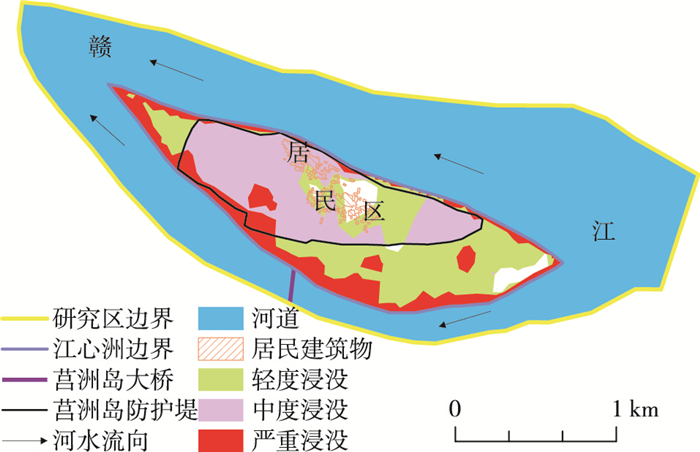
工况1,库区蓄水后,江心洲发生顶托型浸没,当地下水位接近稳定时,发生浸没范围及程度较大(见图 4)。
|
图 4 工况1浸没范围和程度 Figure 4 Immersion range and degree of study area under condition 1 |
工况2与工况1对比,堤外抬田会对江心洲浸没情况产生影响,可控制抬田区域的浸没程度及范围。抬田后,堤内严重浸没面积变小(见表 3),这是因为堤外发生渗漏的区域经抬田后,水流运动到堤内区域时能量损失变大,因此严重浸没面积变小。根据工程要求,后续浸没控制措施均需要配合堤外抬田进行布设,故工况3~14中均加入抬田措施。
工况3,4和5,达到地下水位稳定时需要的时间分别是2个月、10个月和25个月,表明贯穿至砂卵砾石层底部的防渗墙的增长可延长地下水位稳定时间,但最终工况3,4和5浸没面积及程度与工况2相同,故防渗墙仅起到延缓浸没发生的作用,无法控制最终浸没情况。而工况6下地下水稳定所需时间与工况2相同,均为1个月,浸没情况也相同,故贯穿至砂卵砾石层顶板的防渗墙既不能延缓浸没发生,亦不能控制浸没情况。
对比工况7和8,结果显示,井列线位于防护堤和居民建筑物之间时,井列线离防护堤越远,堤内浸没控制效果越好(表 3);井列线离防护堤越远,减压井总流量越小,减压井总流量分别为102 257和80 270 m3/d,其中单井流量分别为403和325 m3/d。
对比工况8,10和9发现,当井径由0.6 m变为0.4和0.2 m时,对应的单井流量为325,295和263 m3/d,相应浸没范围为62 590,143 140和370 180 m2,故随井径变小,流量也会随之降低,浸没范围也会逐渐减小。
对比工况8,11,12和13可知,随着防渗墙添加并由1 736 m到3 592和4 336 m时,相应工况总流量分别为80 270,42 878,11 621和1 418 m3/d,相应浸没范围分别为62 590,53 440,49 630和43 990 m2;故减压井与防渗墙联合布设情况下,当防渗墙添加且加长时,减压井总排水量会随之减小,但浸没范围变化不大。故考虑到工况13和14中防渗墙布设会大范围截断堤后地下水与地表水的水力联系,对堤后居民的正常生产生活造成影响,故在有效控制浸没范围的前提下,选择工况11为宜。
在工况3,4,5,6,11,12和13中,堤内防渗墙处水力坡度最大为28.26,均没有超过工程设定极限值60,故上述工况均符合工程安全要求。
4 结语通过建立地下水三维非稳定流数值模型,对新干航电枢纽工程库区江心洲进行浸没预测与控制,得到以下结论:
(1) 江心洲地势平坦低洼,水库蓄水后,在工况1无浸没控制措施情况下,30 d后居民区发生浸没,堤内外浸没面积占江心洲陆地面积的90.8%。
(2) 堤外进行抬田。抬田对渗漏型浸没产生一定影响,对顶托型浸没基本没影响,堤内主要发生顶托型浸没,局部区域为渗漏型浸没。
(3) 贯穿至砂卵砾石层底部的防渗墙仅延缓地下水浸没的发生,最终浸没情况与未布设防渗墙情况相同。而贯穿至砂卵砾石层顶板的防渗墙既不能延缓浸没的发生,也不影响最终浸没情况。
(4) 减压井是最有效的浸没控制措施,且井列线离莒洲岛防护堤越远,井径越大,堤内浸没效果控制越好。防渗墙与减压井同时布设时,通过设置贯穿至砂卵砾石防渗墙不同长度方案,对比发现在不影响居民用水情况下,最优防渗墙长度为1 736 m(控制点:A→B),同时可大大减小减压井排水量。故联合布设方案,不仅可有效控制研究区浸没情况,且能够有效控制减压井排水量,是最优布设方案。
| [1] |
戚筱俊. 工程地质及水文地质[M]. 北京: 中国水利水电出版社, 1997. ( QI Xiaojun. Engineering geology and hydrogeology[M]. Beijing: China Water Power Press, 1997. (in Chinese))
|
| [2] |
GRAAF I, BEEK L, WADA Y, et al. Dynamic attribution of global water demand to surface water and groundwater resources: Effects of abstractions and return flows on river discharges[J]. Advances in Water Resources, 2014, 64(1): 21-33. |
| [3] |
戴长雷, 李治军, 高淑琴. 大顶子山航电枢纽蓄水后上游临江地区地下水浸没影响态势初步分析[J]. 黑龙江大学工程学报, 2010, 1(1): 45-50. ( DAI Changlei, LI Zhijun, GAO Shuqin. Groundwater immersion situation in riverside regions after Dadingzishan Navigation Hydropower Project storing water[J]. Journal of Engineering of Heilongjiang University, 2010, 1(1): 45-50. (in Chinese)) |
| [4] |
KARATZAS G P. Developments on mdeling of groundwater flow and contaminant transport[J]. Water Resour Manage, 2017, 31(10): 3235-3244. DOI:10.1007/s11269-017-1729-z |
| [5] |
GLEESON T, MANNING A H. Regional groundwater flow in mountainous terrain: three-dimensional simulations of topographic and hydrogeologic controls[J]. Water Resources Research, 2008, 44(10): 297. |
| [6] |
DOBLE R C, CROSBIE R S, SMERDON B D, et al. Groundwater recharge from overbank floods[J]. Water Resources Research, 2012, 48(9): 9522. |
| [7] |
SCIBEK J, ALLEN D M, WHITFIELD P H. Quantifying the impacts of climate change on groundwater in an unconfined aquifer that is strongly influenced by surface water[J]. Geological Society London Special Publications, 2008, 288(1): 79-98. DOI:10.1144/SP288.07 |
| [8] |
骆祖江, 张弘, 李会中, 等. 乌东德水电站坝址区地下水渗流三维非稳定流数值模拟[J]. 岩石力学与工程学报, 2011, 30(2): 341-347. ( LUO Zujiang, ZHANG Hong, LI Huizhong, et al. Three-dimensional transient flow numerical simulation of groundwater seepage in dam site of Wudongde hydropower station[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(2): 341-347. (in Chinese)) |
| [9] |
TAO X, MA J, ZENG W. Treatment effect investigation of underground continuous impervious curtain application in water-rich strata[J]. International Journal of Mining Science and Technology, 2015, 25(6): 975-981. DOI:10.1016/j.ijmst.2015.09.015 |
| [10] |
王晓燕, 党发宁, 田威, 等. 大渡河某水电站围堰工程中悬挂式防渗墙深度的确定[J]. 岩土工程学报, 2008, 30(10): 1564-1568. ( WANG Xiaoyan, DANG Faning, TIAN Wei, et al. Determination of depth of suspended cut-off walls in cofferdam of a hydraulic power station in Dadu River[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(10): 1564-1568. DOI:10.3321/j.issn:1000-4548.2008.10.025 (in Chinese)) |
| [11] |
冶雪艳, 杜新强, 杨悦锁. 绥化市红兴水库渗漏分析及渗控方案模拟预测[J]. 吉林大学学报(地球科学版), 2010, 40(1): 128-133. ( YE Xueyan, DU Xinqiang, YANG Yuesuo. Seepage analysis and forecast of the seepage-control schemes of Hongxing reservior in Suihua City[J]. Journal of Jilin Unviersity (Earth Science Edition), 2010, 40(1): 128-133. (in Chinese)) |
| [12] |
吕路, 杨军耀, 秦嘉楠. 汾河三期蓄水工程人工湖渗漏对太原市浅层地下水影响的数值模拟[J]. 水电能源科学, 2017, 35(1): 89-93. ( LYU Lu, YANG Junyao, QIN Jianan. Numerical simulation of impact of artificial lake leakage on shallow groundwater in Taiyuan in third stage of Fenhe River water storage project[J]. Water Resources and Power, 2017, 35(1): 89-93. (in Chinese)) |
| [13] |
骆祖江, 杨林, 李占军, 等. 松原壅水坝工程库区左岸浸没预测三维数值模拟[J]. 农业工程学报, 2012, 28(3): 129-134. ( LUO Zujiang, YANG Lin, LI Zhanjun, et al. Three-dimensional numerical simulation for immersion prediction of left bank of Songyuan reservoir project[J]. Transactions of the Chinese Society of Agricultural Engineering, 2012, 28(3): 129-134. DOI:10.3969/j.issn.1002-6819.2012.03.023 (in Chinese)) |
| [14] |
曹洪, 尹小玲, 魏旭辉, 等. 潮州供水枢纽工程库区浸没影响初探[J]. 岩石力学与工程学报, 2004, 23(5): 862-866. ( CAO Hong, YIN Xiaoling, WEI Xuhui, et al. Primary study on effects of immersion by reservior of Chaozhou water supply project[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(5): 862-866. DOI:10.3321/j.issn:1000-6915.2004.05.028 (in Chinese)) |
| [15] |
曹剑峰, 迟宝明, 王文科, 等. 专门水文地质学[M]. 北京: 科学出版社, 2006. ( CAO Jianfeng, CHI Baoming, WANG Wenke, et al. Special hydrogeology[M]. Beijing: Science Press, 2006. (in Chinese))
|
| [16] |
钱会, 郑西来, 樊秀峰. 傍河取水越河稳定渗流问题的三维数值模拟研究[J]. 水利学报, 1999(3): 32-37. ( QIAN Hui, ZHENG Xilai, FAN Xiufeng. Numerical modeling of steady state 3-D groundwater flow beneath an incomplete river caused by riverside pumping[J]. Journal of Hydraulic Engineering, 1999(3): 32-37. DOI:10.3321/j.issn:0559-9350.1999.03.006 (in Chinese)) |
| [17] |
曹腾飞.区域地下水评价及影响研究--以新干县地下取用水为例.南昌: 南昌大学, 2015. (CAO Tengfei. Study on regional groundwater assessment and impact--Underground water in Xingan as an example. Nanchang: Nanchang University, 2015. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D691685
|
 2018
2018 
