航道维护底宽是船舶安全航行的重要指标之一,一方面关系着航道管理部门的维护工作量和资金投入,另一方面又影响着航道的通过能力。国内外对航道维护的研究主要集中在维护方法和维护手段。Cowan研究了通过遗传算法来改进航道网络的维护方案[1];Prather等以莫农加希拉河为例,对航道长期运行和维护进行经济性分析[2];德国的Kuehni等研究了基于IT的e-maintenance系统(EMS),从定期检查和各种数学模型中获得数据,结合该系统来确定德国水路网络中的相关基础设施是否需要预防性维护[3]。国内一些学者从影响船舶航行安全、船舶阻力等单因素分析出发提出计算航道底宽的方法[4-7],但对维护尺度与效益及费用等方面研究尚少。
本文以内河限制性航道为对象,从多因素角度探索航道维护底宽确定方法,指导航道维护断面构建,具有实用价值,符合科学管理、绿色发展理念。
1 研究区域和方法京杭运河镇江段按三级限制性航道整治,两岸为直立式护岸,航道底宽45 m,水面宽90 m,设计时采用的1 000 t级标准船型:驳船为65.0 m×10.8 m×2.2 m(船长×船宽×型深),货船为68.0 m×10.8 m×2.6 m。研究中实际抽样调查了京杭运河镇江段船舶载重吨位、船型尺度,统计回归得到1 000 t级实际船型:驳船为48.0 m×10.0 m×2.7 m,货船为56.0 m×11.0 m×2.8 m。京杭运河镇江段谏壁船闸2016年通过船舶数量、吨位及占比见表 1。
| 表 1 谏壁船闸船舶过闸分析 Table 1 Analysis of Jianbi shiplock throughput capacity |
根据水位资料统计分析,京杭运河镇江段每年枯季时间约为60天,洪季约为60天,常水位时间约为240天。
耦合多因素的内河限制性航道维护底宽确定步骤如下:
(1) 分别对设计标准船型和实际统计船型,从满足船舶操纵性和航行可靠性目标出发,基于船舶运动特性和可靠性理论,计算不同条件下所需的航道宽度。
(2) 计算航道维护底宽。根据内河限制性航道断面形态,航道维护底宽与航道宽度的关系如下式所示:
| $ {B_{\rm{b}}} = B - 2m\left( {H - T} \right) $ | (1) |
式中:Bb为航道底宽;B为航道宽度;H为航道水深;m为航道边坡比;T为船舶吃水。
(3) 建立效益-费用模型。在(1)和(2)计算得到的航道底宽范围基础上,进行航道效益和维护费用分析,确定满足最佳效益费用比的航道维护底宽。
(4) 以通航安全为底线,确定安全可靠、效益费用佳的内河限制性航道维护底宽。
2 满足不同条件的内河限制性航道维护底宽 2.1 满足船舶运动特征的航道维护底宽船舶行驶时,受风、流等自然条件及航道断面、助航设施、船舶操纵性和人为因素的影响, 其航行轨迹会在航道中线左右摆动,需要不断地操舵来校正航向、纠正偏航。船舶航行时,所需航宽为航迹带在航宽方向的投影与航道富裕宽度之和[8]。在各种风、流影响情况下,双线航道船舶(队)航行所需航宽主要考虑风致漂移量及流致漂移量,可采用下式进行计算[9],即:
| $ B = {B_{{\rm{Fd}}}} + {B_{{\rm{Fu}}}} + {B_{{\rm{ad}}}} + {B_{{\rm{au}}}} + {B_{{\rm{wd}}}} + {B_{{\rm{wu}}}} + {d_1} + {d_2} + C $ | (2) |
| $ {B_{\rm{a}}} = K \cdot \sqrt {\frac{{{B_A}}}{{{B_{\rm{w}}}}}} \cdot {e^{ - 0.14{V_{\rm{s}}}}} \cdot {V_{\rm{a}}} \cdot S \cdot \frac{{\sin {\alpha _{\rm{f}}}}}{{\left| {V\cos \beta + U\cos \alpha } \right|}} $ | (3) |
| $ {B_{\rm{w}}} = S \cdot \frac{{V\sin \beta + U\sin \alpha }}{{\left| {V\cos \beta + U\cos \alpha } \right|}} $ | (4) |
式中:Bad,Bau分别为船舶下行和上行时的风致漂移量;Bwd,Bwu分别为船舶下行和上行时的流致漂移量;K为风致漂移系数;BA为船体水线上侧受风面积;Bw为船体水线下侧面积;Vs为风中航速;Va为相对风速;αf为真风作用方向与船舶首尾线的夹角;S为计算河长;V为船速;U为流速;α为流向角;β为航行漂角。
京杭运河镇江段常年水位变幅较小、水流平稳,流速U为0.5 m/s,船舶航速Vs为8 km/h,K一般取0.038~0.041,流向角α为2°,航行漂角β为3°,计算河长S取3倍船队长度。由式(1)和(2)得,标准船型和实际船型下考虑船舶运动特性的航道底宽分别为42和39 m。
2.2 满足通航标准的航道维护底宽根据GB 50139—2014《内河通航标准》,直线段航道宽度包括航迹带宽度、船间距离和船离岸距离,航迹带主要包括船舶航行中在航迹线左右的偏移量及船舶本身占用的航道空间,而航行漂角的取值则决定航迹线的左右偏移量,双线航道水深和宽度的计算方法[9-10]见下式:
| $ B = {B_{{\rm{Fd}}}} + {B_{{\rm{Fu}}}} + {d_1} + {d_2} + C $ | (5) |
| $ {B_{{\rm{Fd}}}} = {B_{{\rm{sd}}}} + {L_{\rm{d}}}\sin \beta $ | (6) |
| $ {B_{{\rm{Fu}}}} = {B_{{\rm{su}}}} + {L_{\rm{u}}}\sin \beta $ | (7) |
式中:B为直线段双线航道宽度;BFd,BFu分别为下行和上行船舶或船队航迹带宽度;d1为下行船舶或船队外舷至航道边缘的安全距离;d2为上行船舶或船队外舷至航道边缘的安全距离;C为船舶或船队会船时的安全距离;β为航行漂角。
航行漂角值对船舶航行安全影响较大,GB 50139—2014《内河通航标准》中航行漂角为3°,各项安全距离之和d1+d2+C为上行和下行航迹带宽度和的50%~60%。将标准船型和实际船型代入式(5),得到标准船型和实际船型所需的航道底宽分别为45和44 m。
2.3 满足航行可靠性的航道维护底宽船舶航行可靠性是指在一定的外界条件和环境下保证船舶安全航行的能力。对航道宽度的可靠性分析,根据对不同船舶宽度在不同航道宽度情况下航行事故的统计进行分析,得到航道宽度与事故数或事故百分比间的回归方程[11]为:
| $ {K_{\rm{c}}} = a{\left( {\frac{{{B_{\rm{c}}}}}{{{B_{\rm{s}}}}} - 1} \right)^{ - b}} $ | (8) |
式中:Bc为航道宽度;Bs为船宽;Kc为事故数;a,b为回归方程参数。统计得出,一般双线航道宽度应大于5倍的船宽才能保证船舶航行的可靠性,Kc值应越小越好。
设计标准船型船宽Bs为10.8 m,实际船型船宽Bs为11.0 m;由式(1)及式(8)统计规律得,标准船型和实际船型下考虑航行可靠性的航道底宽分别为39和40 m。
2.4 不同条件下京杭运河镇江段航道维护底宽综合前述各种情况,以标准船型和实际船型为研究对象,京杭运河镇江段在满足通航标准、运动特征和航行可靠性时,航道维护底宽分别为标准船型45, 42, 39 m和实际船型44, 39, 40 m。
3 基于效益-费用模型的航道维护底宽确定 3.1 航道维护的效益模型航道维护涉及的效益主要有船舶运输效益、节能减排效益、替代公路运输效益。
3.1.1 船舶运输效益载体船舶的千吨每千米油耗量指在完成单位运输周转量的时候船舶所消耗的能源总量,用来反应航运对能源的利用程度,也侧面反映出航运的能源配置合理程度以及船舶运输效益。因此,不同吨级船舶千吨千米能耗强度计算公式如下:
| $ {H_n} = eq = e{Q_{油}}/\left( {Gd} \right) $ | (9) |
式中:Hn为第n类船舶千吨千米能耗强度;q为内河船舶千吨千米的油耗强度;Q油为年燃油消耗量(kg);G为年载货量(t);d为航距(km);e为燃料能耗强度(kcal/kg)。
内河船舶千吨千米能耗强度与单位能耗及单位能耗价格乘积即单位运输成本En。据调研,1 000 t级、800 t级、500 t级、300 t级货船所对应的En分别为63.68, 76.64, 93.82和124.26元/(kt·km)。
在分析论证运输船舶的营运经济效益时,大多采用RFR(必要运费率)和AAC(单位运输成本)两个主要考核指标[12-13],这里以运输成本为指标,分析不同底宽条件下,影响不同等级的船舶航行时所产生的总的船舶运输效益。
综合研究航段船舶等级及对应单位运输效益,船舶运输总效益公式如下:
| $ {F_1} = \sum\limits_n {{E_n}{a_n}} $ | (10) |
式中:F1为每年每千米运输总效益;En为第n类船舶对应单位运输成本;an为第n类船舶吨级对应的运输总量。
当航道底宽变小时,相应等级的船舶航行受到影响,在水深条件满足的情况下,航道底宽仅影响双线船舶交汇,根据京杭运河镇江段实地观测及船舶流量资料,货运影响量为航道枯季上下行货运量的各10%。
由式(10),结合表 1及各等级船舶单位运输成本,所产生的运费效益见表 2。
| 表 2 镇江段航道每年每千米运费效益 Table 2 Transport benefit per kilometre per year of Zhenjiang reach |
船舶航行节能减排效益主要分为直接效益和间接效益两部分,直接效益是指航行阻力减小带来的节能效益,间接效益则是公路与水运之间货运量的转移而产生的碳排效益。
(1) 船舶航行节能效益:航行阻力是影响船舶节能减排效益的直接因素,主要与船舶航速以及航道断面有关,航道断面系数增大,航行阻力减小,能耗减小,从而实现节能效益,因此,节能减排直接效益计算式为:
| $ {F_2} = \sum\limits_n {\left( {\frac{{{K_n}}}{{{K_0}}} - 1} \right){c_n}{a_{\rm{f}}}} $ | (11) |
式中:F2为确定底宽下每年每千米节能减排直接效益;cn为第n类船舶平均每千米耗油(kg);Kn为定底宽下不同吨级船舶对应的航道断面阻力系数;K0为航行阻力不影响船舶通行时的阻力系数;af为每千克耗油单价(元/kg)。
据镇江段实地调研,船舶航行经济船速为8 km/h,当断面系数n>7时,航行阻力不影响船舶通行时的阻力系数K0=1.8(见图 1)。不同吨级船舶平均每千米每千吨消耗柴油为:100 t级船舶10.2 kg,200~300 t级船舶8.4 kg,300~500 t级船舶6.2 kg, 500~1 000 t级船舶2.9 kg。考虑到江苏省内柴油价格为6.81元/kg,则不同维护底宽条件下镇江陵口段每年每千米节能减排直接效益见表 3。
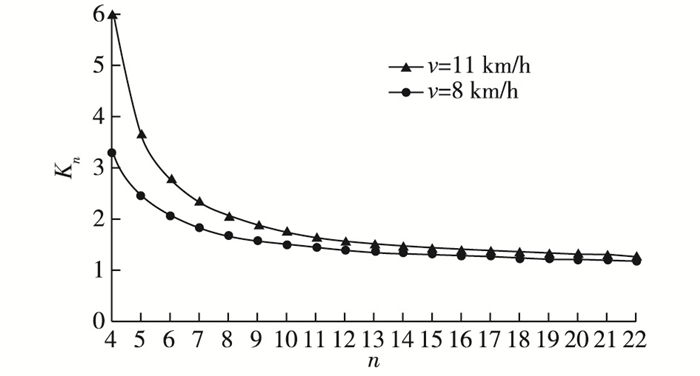
|
图 1 船舶阻力换算系数与断面系数之间的关系[14] Figure 1 Relationships between ship resistance conversion coefficient and section coefficient[14] |
| 表 3 镇江段航道每年每千米节能减排直接效益 Table 3 Direct benefit of energy saving and emission reduction per kilometre per year of Zhenjiang reach |
(2) 节能减排间接效益:当航道维护底宽不同时,航道断面则会影响相应等级船舶通航,从而使得部分船舶货运量转移到公路运输,由于公路运输相比水路运输碳排放量大量增加,因此,需计算该类碳排放所带来的社会效应。
根据《2006年IPCC国家温室气体清单指南》[15],可采用交通运输方式的燃料单位里程消耗量与行车里程的乘积所得到碳排放量,再乘以每种燃料的排放系数。节能减排间接效益计算公式如下:
| $ {F_3} = \sum\limits_n {{P_n}{\beta _1}{r_{\rm{0}}}} $ | (12) |
式中:F3为每年每千米节能减排间接效益;Pn为第n类船舶载质量(103t);β1指交通方式碳排放因子(β1的取值为公共汽车0.066,轨道交通0.042,私家汽车0.239,出租车0.276,货运车0.141);r0为单位体积碳排放量造成的社会效益。
目前,碳排放量价格为77~93元/t[16],这里取85元/t,碳排放增量间接效益见表 4。
| 表 4 镇江段航道每年每千米节能减排效益 Table 4 Benefit of energy saving and emission reduction per kilometre per year of Zhenjiang reach |
当航道进行疏浚施工时,受到施工区域水域的限制,部分水路货运量会改走陆运。水运和陆运相比,转移运量使得总耗油量增加,替代公路运输效益公式如下:
| $ {F_4} = W \times L \times \left( {{q_2} - {q_1}} \right) \times {a_{\rm{f}}} $ | (13) |
式中:F4为替代公路运输效益;W为年货运量(103t);L为运距(km);q2为公路单位运输油耗(kg);q1为水运单位运输油耗(kg);af为每千克耗油单价(元/kg)。
根据镇江市交通统计资料,公路水路的柴油消耗量差为25.3 kg/(103t·km),由式(13)计算得每年每千米节约资金见表 5。
| 表 5 镇江段航道每年每千米替代公路运输效益 Table 5 Benefit of substitutes for highway per kilometre per year of Zhenjiang reach |
航道维护费包括疏浚作业及日常维护两方面,主要以疏浚量为指标,即计算实际断面与维护标准之间的回淤量,每米航道疏浚费用计算式如下:
| $ {C_0} = {C_1} \times {V_s} + {C_2} $ | (14) |
式中:C0为每延米航道疏浚费用;C1为每立方米疏浚费用;Vs为每延米航道疏浚量(m3);C2为航道日常维护费用。
江苏内河疏浚主要采用液压抓斗式挖泥船,抓斗容量一般为0.75~1.00 m3,镇江段疏浚单价为17元/ m3。根据《疏浚工程技术规范》(JTJ 319—1999),各挖泥船的每边计算超宽、超深分别为2.0和0.3 m。由式(14)计算不同维护底宽条件下航道每千米疏浚量及疏浚费用见表 6。
| 表 6 镇江段航道不同维护底宽下疏浚量及费用 Table 6 Dredging amount and cost under different maintenance bottom widths at Zhenjiang reach |
最佳养护时机应是在费用较小而效益较大时,即效益费用比FBCR最大时,采用有效性指标FBCR计算:
| $ {F_{{\rm{BCR}}}} = {B_i}/{C_i} $ | (15) |
式中:Bi为不同情况下的总效益;Ci为不同情况下的总费用。
通过比较FBCR的大小,当FBCR < 1时,认为航道维护总效益小于总费用,此时航道维护不合理,因此选择最大FBCR值对应的航道底宽即是预防性养护措施最佳时机。
由式(15)计算京杭运河镇江陵口段不同维护底宽效益费用比见表 7。
| 表 7 运河镇江段航道不同维护底宽下效益费用比 Table 7 Ratio of benefit and cost under different maintenance bottom widths in Zhenjiang channel |
由图 2可见,当航道维护底宽大于39 m时,航道总效益与总维护费用的比值随维护底宽的增大而减小,维护底宽取39 m时,效益费用比FBCR最大最经济。本研究航段满足实际船型航行可靠性的航道维护底宽需要40 m。因此,综合效益与费用及航行安全性,研究航段维护底宽定40 m较为合理。

|
图 2 镇江段航道FBCR值与航道维护底宽关系 Figure 2 Relationships between FBCR value and maintenance bottom width in Zhenjiang reach of Beijing-Hangzhou Canal |
通过建立的限制性航道维护底宽的效益-费用模型,可计算航道效益费用比最大条件下的维护底宽。综合运用效益-费用模型以及船舶运动特性、航行可靠性分析法等,最终确定限制性航道的维护底宽,并应用到京杭运河镇江段实例计算中。分析研究结果表明,该方法能较好地考虑到限制性航道的通航因素及经济需求,具有较高实用价值。
| [1] |
MITCHELL K N, WINTON C, COWAN M. Improved waterway network maintenance strategies via geneticalgorithms[J]. Transportation Research Board Annual Meeting, 2015. |
| [2] |
PRATHER L J, WISE H. Economic analysis for long-term operation and maintenance of a waterway: the case of the Monongahela River[J]. Economic Analysis, 1989(1222): 46-53. |
| [3] |
KUHNI K, BODEFELD J, KUNZ C, et al. EMS-WSV-EinErhaltungs management system fürVerkehrswasserbauwerke[J]. Bautechnik, 2008, 85(8): 514-520. DOI:10.1002/bate.200810039 |
| [4] |
刘娜.天津港水深动态维护应用研究[D].天津: 天津大学, 2010. (LIU Na. Applied research on dynamic maintenance of water depth in Tianjin port[D]. Tianjing: Tianjing University, 2010. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10056-2010209613.htm
|
| [5] |
刘玙.内河航道维护水平评价研究[D].武汉: 武汉理工大学, 2013. (LIU Yu. Study on evaluation of inland waterway maintenance level[D]. Wuhan: Wuhan University of Technology, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10497-1014159837.htm
|
| [6] |
丁坚, 姚建卫, 李安中, 等. 江苏省内河航道养护和管理规划研究[J]. 水运工程, 2009(10): 102-106. ( DING Jian, YAO Jianwei, LI Anzhong, et al. Conservation and management planning of inland waterway of Jiangsu Province[J]. Port and Waterway Engineering, 2009(10): 102-106. (in Chinese)) |
| [7] |
WOHL E. Particle dynamics: the continuum of bedrock to alluvial river segments[J]. Geomorphology, 2015, 192-208. |
| [8] |
曹民雄, 马爱兴, 王秀红, 等. 内河航道横流对船舶航行的影响[J]. 交通运输工程学报, 2008, 8(1): 61-67. ( CAO Minxiong, MA Aixing, WANG Xiuhong, et al. Influence of cross current on ship navigation in inland waterway[J]. Journal of Traffic and Transportation Engineering, 2008, 8(1): 61-67. DOI:10.3321/j.issn:1671-1637.2008.01.013 (in Chinese)) |
| [9] |
饶思梁.内河航道尺度与通航能力关系研究[D].武汉: 武汉理工大学, 2011. (RAO Siliang. A study on the relationship of inland waters channel dimensions and navigation capacity[D]. Wuhan: Wuhan University of Technology, 2011. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10497-1011104170.htm
|
| [10] |
GB 50139-2014内河通航标准[S]. (GB 50139-2014 Navigation standard of inland waterway[S]. (in Chinese))
|
| [11] |
甘浪雄. 航道条件对船舶航行可靠性的影响[J]. 中国航海, 2001(2): 55-57. ( GAN Langxiong. The effect of channel conditions on ship navigation[J]. Navigation of China, 2001(2): 55-57. DOI:10.3969/j.issn.1000-4653.2001.02.012 (in Chinese)) |
| [12] |
张国民. 黄河中游100吨级浅吃水船型及单船运输效益的研究与分析[J]. 山西交通科技, 1997(6): 53-57. ( ZHANG Guomin. Research and analysis of 100 t shallow water ship model and single ship transportation benefit[J]. Shanxi Traffic Science and Technology, 1997(6): 53-57. (in Chinese)) |
| [13] |
刘灿齐, 樊建林, 徐瑞华. 城市轨道交通成本、效益及其利益转移分析[J]. 上海铁道大学学报, 2000, 21(2): 56-60. ( LIU Canqi, FAN Jianlin, XU Ruihua. Analysis of cost, benefit and inner transference of urban rail-transit[J]. Journal of Shanghai Tiedao University, 2000, 21(2): 56-60. DOI:10.3969/j.issn.1008-0392.2000.02.013 (in Chinese)) |
| [14] |
周华兴, 郑宝友. 关于深水、浅水与限制性航道界定的探讨[J]. 水运工程, 2006(1): 53-58. ( ZHOU Huaxing, ZHENG Baoyou. Discussion on defining deep water, shallow water and restricted channel[J]. Port and Water Engineering, 2006(1): 53-58. DOI:10.3969/j.issn.1002-4972.2006.01.013 (in Chinese)) |
| [15] |
PAUSTIAN K, RAVINDRANATH N H, AMSTEL V A, et al. 2006 IPCC guidelines for national greenhouse gas inventories[M]. Hayama: IGES, 2006.
|
| [16] |
陈晓红, 王陟昀. 碳排放权交易价格影响因素实证研究--以欧盟排放交易体系(EUETS)为例[J]. 系统工程, 2012(2): 53-60. ( CHEN Xiaohong, WANG Zhiyun. Empirical research on price impact factor of carbon emission exchange: evidence from EUETS[J]. Systems Engineering, 2012(2): 53-60. (in Chinese)) |
 2018
2018 