2. 河海大学港口海岸与近海工程学院,江苏 南京 210098;
3. 南京水利科学研究院,江苏 南京 210029
港湾受到与其固有频率相接近的波浪入射时,港池内会出现大幅波动现象,即称之为港湾共振[1]。港湾的共振频率与共振模态是其固有属性,主要由几何形状和地形决定。港湾共振的振幅可达到入射波高的几倍甚至几十倍,从而严重影响港内停泊船只,降低港口运行效率,甚至破坏码头建筑物。因此有必要分析研究港湾共振的机理,优化布局设计并改善港湾的动态响应,从而最大程度地降低港湾共振的危害。
早期的港湾共振研究主要关注平面形状和水底地形极其简单的港口。Mcnown[2]在假定发生港湾共振时驻波波腹位于口门处的条件下,研究了小开口圆形港池的响应特性。Miles等[3]采用格林函数为基础的积分方程分析与外海直接相连的小开口细长港的共振条件,并且给出了最大波幅放大系数的解析表达式。Ippen等[4]应用傅里叶变换法结合边界条件得到了矩形港池共振的解析解。Lee[5]通过求解Helmholtz方程给出了具有10°和60°开口的圆形港池的解析解。早期这些波浪数值模型是基于线性控制方程的,无法精确模拟港内外波浪间复杂的非线性过程。近年来,Boussinesq方程不断发展,已成为一种比较理想的描述非线性波浪在近岸水域传播变形的模型,在港湾共振领域应用广泛。Nwogu[6]采用基于有限差分法的Boussinesq类模型研究了短波波群引起的港内长周期振荡。Dong等[7]利用Boussinesq模型模拟了狭长矩形港池分别在单色波和双色波群入射时引起的港内长周期振荡,研究了非线性港湾振荡的能量传递和衰减过程。马小舟等[8-9]使用MIKE21-BW模块模拟了多种类型的港池对孤立波和白噪声的响应。史宏达等[10]应用MIKE21-BW模块计算了不同入射波周期、不同的港池口门宽度和位置引起的矩形港池内的波高分布。郑金海等[11]应用Boussinesq模型模拟了矩形及其扩展形状港湾内的水波共振现象。高俊亮等[12-13]采用完全非线性Boussinesq模型模拟了由双色波群诱发的常水深狭长型矩形港内的二阶长波共振现象,并研究了在不同共振模态下港内锁相和自由长波波幅以及它们的相对成分与入射短波波长和波幅的关系。高俊亮等[14-15]使用完全非线性Boussinesq方程模拟了孤立波和多种N波入射常水深狭长型矩形港池引起的港湾振荡现象,研究了入射波类型及波幅对港内相对波能分布的影响,分析了港内波高放大因子随入射波高的变化规律。
前人的研究都是对细长港池和矩形港池进行波浪数值模拟并分析其共振响应,但是对孤立波进入较复杂的组合型港池时引起港湾共振的响应过程较少涉及。本文通过改变港口的平面布置形式得到多种类型的组合型港池,利用MIKE21-BW模块模拟孤立波在进入一侧为开敞水域的常水深组合型港池时引发的港池内水体的共振响应现象,并借助频谱和波幅分布研究港池内水体的响应特性和共振规律。
1 控制方程连续方程:
| $ n\frac{{\partial \xi }}{{\partial t}} + \frac{{\partial P}}{{\partial x}} + \frac{{\partial Q}}{{\partial y}} = 0 $ | (1) |
X方向动量方程:
| $ \begin{array}{*{20}{c}} {n\frac{{\partial P}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{{P^2}}}{h}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{xx}}}}{{\partial x}} + \frac{{\partial {R_{xy}}}}{{\partial y}} + {F_x}{n^2}gh\frac{{\partial \xi }}{{\partial x}} + }\\ {{n^2}P\left( {\alpha + \beta \frac{{\sqrt {{P^2} + {Q^2}} }}{h}} \right) + \frac{{gP\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\mathit{\Psi }_1} = 0} \end{array} $ | (2) |
Y方向动量方程:
| $ \begin{array}{*{20}{c}} {n\frac{{\partial Q}}{{\partial t}} + \frac{\partial }{{\partial y}}\left( {\frac{{{Q^2}}}{h}} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{PQ}}{h}} \right) + \frac{{\partial {R_{yy}}}}{{\partial y}} + \frac{{\partial {R_{xy}}}}{{\partial x}} + {F_y}{n^2}gh\frac{{\partial \xi }}{{\partial y}} + }\\ {{n^2}Q\left( {\alpha + \beta \frac{{\sqrt {{P^2} + {Q^2}} }}{h}} \right) + \frac{{gQ\sqrt {{P^2} + {Q^2}} }}{{{h^2}{C^2}}} + n{\mathit{\Psi }_2} = 0} \end{array} $ | (3) |
式中:n为孔隙率;ξ为水位(m);t为时间(s);x, y为笛卡尔坐标(m);P, Q分别为x, y方向的流量密度(m3/(s·m));h为水深(m),h=d+ξ,d为静止水位时水深(m);Rxx, Ryy和Rxy为水滚引起的非均匀流动所产生的附加质量;g为重力加速度(m/s2);Ψ1和Ψ2为Boussinesq方程的色散项;Fx, Fy为x, y方向的水平应力;α为多孔介质中的层流阻力系数;β为多孔介质中的湍流阻力系数;C为谢才阻力系数。
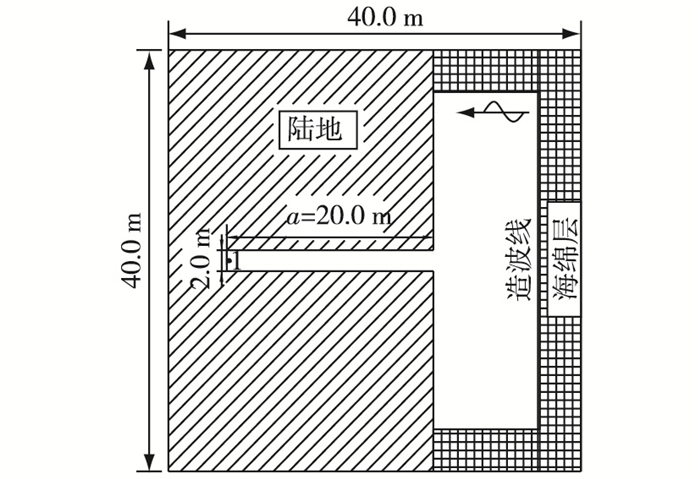
2 模型验证 2.1 细长港池模型本节采用长a=20.0 m,宽b=2.0 m的平底细长港池模型进行波浪数值模拟,港内外水深均为常水深1.0 m,如图 1所示。整个模拟区域尺寸为40.0 m×40.0 m,细长港池尺寸为2.0 m×20.0 m,网格尺寸为dx=dy=0.2 m。为了降低边界对港内波浪的影响,将口门外的水域宽度设为40.0 m,在距离岸线16.0 m和上下两侧的开边界处布置宽为Lsp=4.0 m的海绵层用来吸收开边界处的波浪能量,港内3个壁面均为直立固壁边界,即波浪在该处为全反射状态。造波方式采用域内造波,造波线布置在海绵层前沿,距离口门12.0 m,入射波垂直于岸线正向进入港内。测点1在港池中轴线上,距左侧固壁距离为0.2 m(见图 1)。
|
图 1 细长港池平面布置 Figure 1 Layout of narrow long harbor |
孤立波是存在于自然界中的一种独特的波动现象,其运动过程可以用Kdv方程(Korteweg-de Vries equation)描述,波面方程η的表达式可写成如下形式:
| $ \eta = H{\rm{sec}}{{\rm{h}}^2}\left[ {\sqrt {\frac{{3H}}{{4{h^3}}}\left( {x - vt} \right)} } \right] $ | (4) |
式中:η为静水面至孤立波波面距离;H为波高;h为水深;x为水平坐标;t为时间;
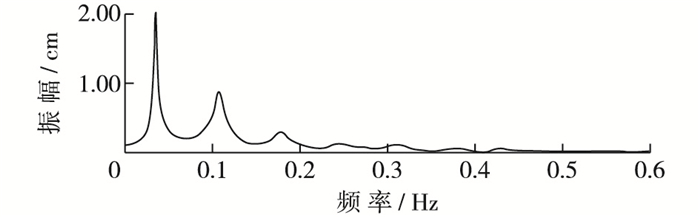
入射波为孤立波,波高H=0.1 m,模型模拟时间为400 s,时间步长为dt=0.02 s。由于港内波浪运动比较复杂,各个测点处波浪能量集中状况有所差别。根据Mei[16]分析,位于港池最内侧的测点1可以代表港内的波动形态,因此选测点1为参考点分析整个细长港内的波浪情况。基于傅里叶变换得到测点1的频谱如图 2所示。
|
图 2 细长港池测点1波浪频谱 Figure 2 Amplitude spectrum at point 1 of the narrow long harbor |
同时,采用邹志利[17]的狭长型矩形港池共振频率解析解,当波浪的波数k满足式(5)时,该波浪在港湾内引起的共振振幅最大。
| $ {k_m} = {k_m}^\prime \left( {1 + \frac{b}{{{\rm{ \mathsf{ π} }}a}}\ln \frac{{\sqrt 2 \gamma {k_m}^\prime b}}{{4{{\rm{e}}^{3/2}}}}} \right) $ | (5) |
式中:
因此,共振频率fm可表示为:
| $ {f_m} = \frac{{{{\left( {g{k_m}\tanh \left( {{k_m}h} \right)} \right)}^{1/2}}}}{{2{\rm{ \mathsf{ π} }}}} $ | (6) |
由解析解求得的共振频率与数值模拟得出的前3个共振模态的响应频率的数值见表 1。
| 表 1 细长港池测点1的响应频率和理论共振频率 Table 1 Response frequency and natural frequency at point 1 in the narrow long harbor |
通过对比可以看出,细长港池中测点1在孤立波入射时的响应频率与邹志利的理论共振频率基本一致,表明由孤立波入射引起的波动能量主要集中在港池的各个固有频率上,可以采用孤立波入射来估算常水深细长港池的固有频率。
3 组合型港池计算过程及结果分析本节采用第2节中细长港池模型的区域和网格设置,通过改变细长港池的平面布置形式,建立了两个组合型港池模型,一个是内外港池长度改变的组合型港池,另一个是内外港池连接位置改变的组合型港池。
3.1 内外港池长度变化下港内共振规律研究组合型港池的模型设置和网格尺度与第2节细长港池相同,平面布置形式如图 3所示。宽度b=2.0 m,c为内部港池长度(上端固壁中点至内外港池中心线的交点),d为外部港池的长度(口门中点至内外港池中心线的交点),c+d=20.0 m,即总长度与细长型港池长度相等。测点1~3均在港池中心线上,测点1距上端固壁距离为0.2 m,测点2距离测点1为9.0 m,测点3距离测点2为9.0 m。入射波为孤立波,波高H=0.1 m,时间步长为dt=0.02 s,整个模拟的时间为400 s。

|
图 3 内外港池长度变化下组合型港池平面布置 Figure 3 Layout of combined harbor with change of length of inner and outer harbors |
由于港池总长度c+d不变,改变内部港池长度c,同时外部港池长度d也随之改变,从而得到不同平面布置形式的组合型港池。对各个不同长度c的组合型港池进行波浪数值模拟,并利用傅里叶变换做出各测点的频谱图,不同长度c取值下,各测点主要共振模态的响应频率及振幅的变化趋势如图 4所示。
|
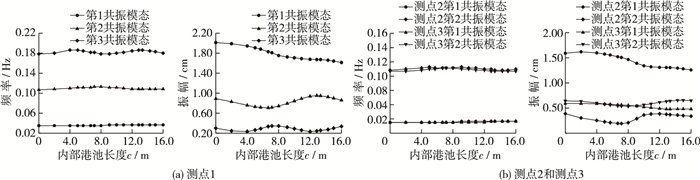
图 4 内外港池长度变化下各测点的共振模态的响应频率和振幅 Figure 4 Response frequency and amplitude of resonance modes at each measurement point under changes of length of inner and outer harbors |
由于具有孤立波特性的波动成分诱发的港湾共振的波浪能量主要集中在最低的两个模态,且测点2和测点3的第3共振模态振幅很小,因此本节只统计了位于波腹点的测点1的第3共振模态的频率和振幅。由图 4可见孤立波在组合型港池中激发的第1和第2共振模态的响应频率与细长港池(c=0)的第1和第2共振模态的响应频率基本保持一致,第3共振模态的响应频率随着内部港池长度c的变化略有波动,但总体上仍接近细长港池(c=0)的第3共振模态的响应频率。因此对于同种类型的组合型港池,可用与其港池总长度相等的细长港池来估算其固有频率。同时可以看到,测点1与测点2和3的对应模态的频率基本相等,这说明港内各个模态的形状没有发生改变,因此可以选择最内侧壁面上的点来表征港内的波动形态。
随着内部港池长度c的增大,第1共振模态的振幅大致呈线性的下降趋势,第2共振模态和第3共振模态的振幅随c的增长呈现波动变化。第2共振模态的波长约为28.0 m,如图 5所示,当内部港池壁面1与壁面2之间的距离为半个波长14.0 m,即c=13.0 m(约为港池总长度的2/3),第2共振模态在壁面1与壁面2之间形成驻波,导致振幅加强,达到最大值;当外部港池口门至壁面3为半个波长14 m,即c=7.0 m(约为港池总长度的1/3),振幅减小至最小值。同样,第3共振模态的波长约为17.0 m,当内部港池壁面1与壁面2之间的距离为半波长的整数倍8.5 m和17.0 m时,即c=7.5和16.0 m时,第3共振模态在壁面1与壁面2之间形成驻波,导致振幅增大至最大值;当外部港池口门至壁面3为半波长的整数倍8.5和17.0 m时,即c=4.0和12.5 m时,振幅减小至最小值。以上分析表明,组合型港池对于减轻港湾共振有一定的作用,但要合理设置内外港池长度,并尽量使内部港池长度不等于可能出现的共振模态的半波长的整数倍,外部港池长度等于半波长的整数倍。

|
图 5 内部港池和外部港池位置示意 Figure 5 The location illustration of inner and outer harbors |
同时港内也产生了其他类型的共振,由于内部港池壁面1与外部港池壁面2之间能够形成驻波,因此在c=5.7,6.7和8.0 m附近时,港内又出现了较大振幅的高频成分的波浪。
设壁面1至壁面2的距离为l,水深恒为h,当波浪在港池内形成驻波时,则在港池边壁y=0与y=l处必然满足全反射条件,有:
| $ \frac{{\partial n}}{{\partial y}} = 0\;或\;\frac{{\partial \varphi }}{{\partial y}} = 0\;\;\;\;y = 0,1 $ | (7) |
所以驻波对应的波数与距离l应满足:
| $ {k_n}l = n{\rm{ \mathsf{ π} }} $ | (8) |
式中:n=1, 2, …为共振的模态,通常存在n个波节点,则对应于第n模态。
自由水面运动可以表示为:
| $ {\eta _n}\left( {y,t} \right) = A\cos \left( {{k_n}y} \right)\cos \left( {{\omega _n}t} \right) $ | (9) |
其中,第n模态共振的波数与频率应满足关系:
| $ \omega _n^2 = g{k_n}\tanh \left( {{k_n}h} \right) $ | (10) |
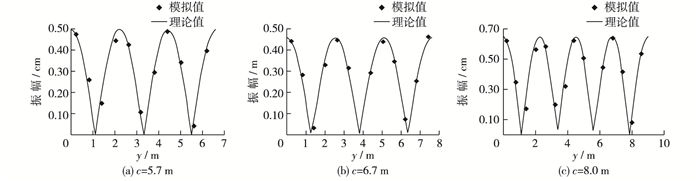
测点1得到的其他类型共振模态的响应频率,与水波理论驻波解推求的共振频率对比见表 2。在壁面1至壁面2之间从测点1开始,每隔0.6 m设置1个测点分析港内波动特性,得到其波幅分布情况,见图 6。
| 表 2 内外港池长度变化时其他类型共振的响应频率和理论共振频率 Table 2 Response frequency and theoretical resonance frequency of other types of resonances with changes of length of inner and outer harbors |
|
图 6 内外港池长度变化时其他类型共振的波幅分布 Figure 6 Amplitude distribution of other types of resonances with change of length of inner and outer harbors |
由以上分析可见,在孤立波正向入射下,这种组合型港池内不仅可以激发与细长港池相同类型的共振响应,还可以在内部港池中形成较大波幅的驻波,而且壁面1至壁面2之间激发的共振响应和驻波理论的解析解非常相符。
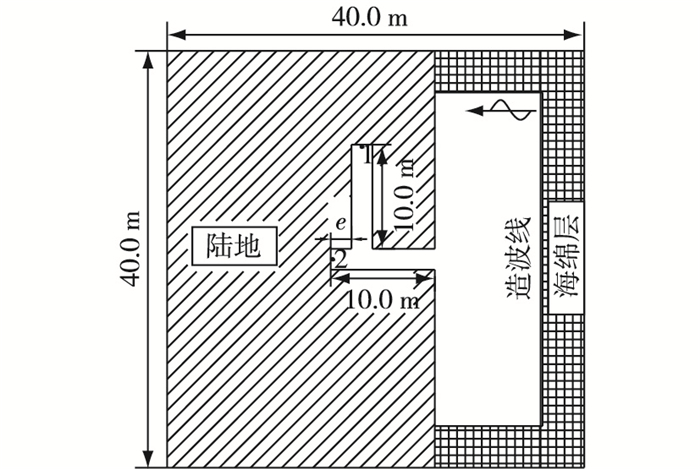
3.2 连接位置变化下港内共振规律研究将内外两个港池的长度固定为10.0 m,改变内外两个港池的连接位置,平面布置见图 7。用长度e表示连接位置的变化量,e越大,则内部港池口门越靠近外部港池口门。由于内外两港池口门位置太近会产生较大的数值耗散,因此本文e最大取5.8 m,即内部港池右侧固壁边界距离外海2.2 m。测点1在内部港池中,距上端固壁距离为0.2 m,测点2在外部港池中,距左端固壁距离为0.2 m。入射波为孤立波,波高H=0.1 m,时间步长为dt=0.02 s,模拟时间为400 s。
|
图 7 连接位置变化下组合型港池平面布置 Figure 7 Layout of combined harbor with change of connecting position |
对各个不同偏移量e的组合型港池进行波浪数值模拟,并利用傅里叶变换分别做出测点1和测点2的频谱图,不同偏移量e取值下,测点1和测点2仅有前两个共振模态一直存在,因此取前两个共振模态所对应的频率及振幅做变化分析(见图 8)。

|
图 8 连接位置变化下测点1和测点2前两个共振模态的响应频率和振幅 Figure 8 Response frequency and amplitude of first two resonant modes at point 1 and point 2 with change of connecting position |
由图 8可见,随着偏移量e的增大,组合型港池的第1共振模态的频率逐渐减小,第2共振模态的频率逐渐增大,这是由偏移量e的不断增大导致壁面1至口门处的距离逐渐缩短导致的,即该组合型港池的前两个共振模态是在波浪位于壁面1至口门处形成的,这与邹志利[17]的狭长型矩形港池的共振频率解析解计算所得的变化趋势一致。随着偏移量e的增大,第1共振模态的振幅呈线性下降的趋势,由于港内波况复杂,不同频率波浪相互作用发生波能传递,第2共振模态的振幅变化呈现出波动增长的趋势,在e=3.0 m附近,壁面1至壁面3之间形成了较大振幅的驻波,导致第2共振模态的振幅相对减小。总之,港内前两个共振模态的振幅与内外两港池的连接位置密切相关,两港池口门之间的距离越小,第1共振模态的振幅越小,第2共振模态的振幅越大。
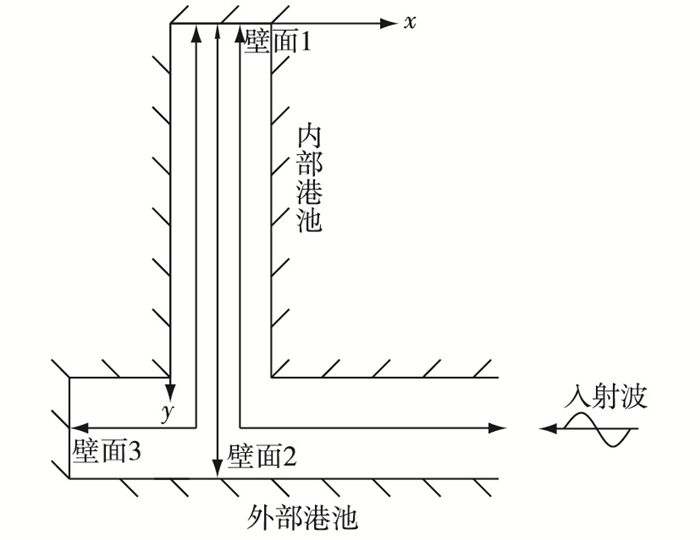
同时,在偏移量e不同的情况下,有不同类型的其他共振产生。如图 9所示,e≤0.5 m时,波浪在壁面1至壁面2之间产生了第3、第4和第5模态共振,但振幅不大且几乎相等,约为壁面1至口门之间的第1共振模态振幅的1/5,e=1.0 m左右时,主要是壁面1至壁面2之间的第3模态共振,振幅较大几乎与壁面1至口门之间的第2共振模态的振幅相当,当e≥2.0 m时,壁面1至壁面2之间的共振几乎消失,同时产生了壁面1至壁面3之间的第2模态共振,且振幅较大,约为壁面1至口门之间的第1共振模态振幅的2/3。因此可见,随着偏移量e的增大,港内形成的较高模态振幅逐渐减小,较低模态振幅逐渐增大。
|
图 9 内部港池和外部港池位置示意 Figure 9 Location illustration of inner and outer harbors |
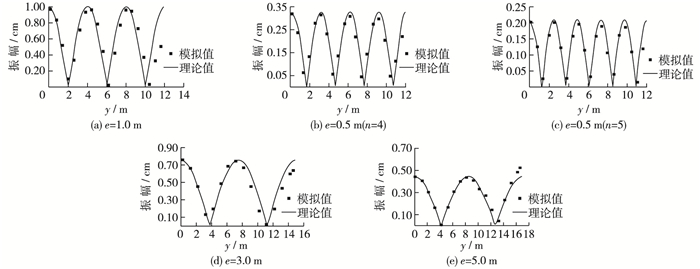
由测点1得到的其他类型的共振模态的响应频率,与水波理论的驻波解推求的共振频率对比并计算相对误差列于表 3。在壁面1至壁面2之间从测点1开始,每隔0.6 m设置1个测点,在壁面1至壁面3之间每隔1.0 m设置1个测点,分析港内波动特性并绘出其波幅分布与理论对比,如图 10所示。
| 表 3 连接位置变化时其他类型共振的响应频率和理论共振频率 Table 3 Response frequency and theoretical resonance frequency of other types of resonances with change of connecting position |
|
图 10 连接位置变化时其他类型共振的波幅分布 Figure 10 Amplitude distribution of other types of resonances with change of connecting position |
由图 10可见,孤立波正向入射下,该种组合型港池的各个其他类型共振模态的响应频率与驻波理论的解析解较为符合,壁面1至壁面2之间形成的驻波振幅在y≥10 m时由于水面变宽而有所减小。此外还可以看出,孤立波入射下组合型港池不仅可以在内部港池与正对其口门的壁面之间形成驻波(壁面1至壁面2),还可以在内部港池和平行于港池纵向的壁面之间形成驻波(壁面1至壁面3)。
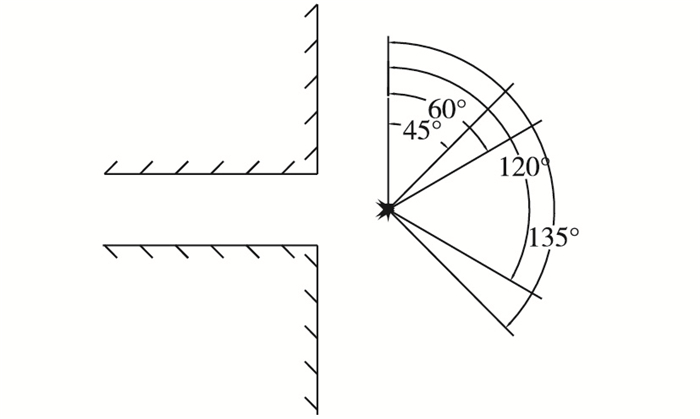
4 影响因素分析 4.1 不同波浪入射方向对港内共振的影响上一节的模拟均采用孤立波正向入射模型港池,实际中的港池有可能受到来自不同方向的波浪入射。本节采用第3节的计算模型和入射波参数,选取了内部港池长度c分别为10.0,16.0 m和偏移量e为5.8 m的组合型港池,模拟了不同方向的入射孤立波进入港内引起的共振现象,入射波传播方向分别与岸线夹角呈45°, 60°, 120°, 135°,如图 11所示。取图 3和图 7中的测点1,计算各个共振模态对应频率,结果见表 4。
|
图 11 入射波传播方向 Figure 11 Schematic diagram of incident wave propagation direction |
| 表 4 不同波浪入射方向下组合型港池主要共振模态的频率 Table 4 Frequency of main resonant modes of a combined harbor in different wave directions |
一般认为狭长型矩形港池内仅存在纵向共振,即横向共振很小,可以忽略不计,因此入射波方向对狭长型矩形港内各个共振模态的形成几乎没有影响。本节所采用的组合型港池均为狭长型,模拟结果显示,在不同方向的孤立波入射下,组合型港池港内并无新增的共振模态产生,同时港内几个主要共振模态的频率都保持在其固有频率附近,不同入射方向的同一共振模态的频率相差很小。然而由于入射波与岸线的夹角不同,导致进入港内的波能不同,从而使斜向入射下各模态的振幅均小于正向入射下的振幅。综上所述,不同波浪入射方向对港内形成的各个共振模态的频率影响不大,即无论是斜向入射还是正向入射,港内激发的各个共振模态的形状都没有改变,因此可以采用孤立波正向入射来估算狭长组合型港池的固有频率。
4.2 部分反射边界对港内共振的影响我国沿海地区波浪的周期一般为4~8 s,设计坡度为1:1.5的护面块石反射系数大约为0.4。本节在所用模型港池的特定内壁直立墙处添加孔隙层,以模拟周期为8 s的波浪在该边界处的部分反射,反射系数为0.4。计算模型和入射孤立波参数设置与第3节港池边界为全反射的模型相同。
选取前述两种组合型港池来研究部分反射边界对港内共振的影响。一种是内部港池长度c=10.0 m的组合型港池,选择壁面1为部分反射边界;另一种是偏移量e=2.0 m的组合型港池,分别选择壁面1和壁面3为部分反射边界。模拟结果取图 3测点1和图 7测点1、测点2做傅里叶变换得到频谱图并与全反射边界条件的频谱图比较,结果列于表 5和表 6。可见,通常情况下改变港湾的边界条件,对港湾内的共振长波影响不大,即设置护面块石来减小港湾共振的效果有限。这是因为长波能量不易被消减或吸收,故仅仅改变边界条件(如陡坡改成缓坡、不透水堤岸改成透水性好的堤岸等),收效并不明显。
| 表 5 不同反射边界条件下内部港池长度c=10.0 m的组合型港池共振模态比较 Table 5 Comparison of resonant modes of combined harbor with inner pool length c=10.0 m under different reflective boundary conditions |
| 表 6 不同反射边界条件下偏移量e =2.0 m的组合型港池共振模态比较 Table 6 Comparison of resonant modes of the combined harbor with offset e=2.0 m under different reflective boundary conditions |
然而减小边界的反射系数对于优化港内波况有较大益处,图 12为全反射和部分反射边界(反射系数0.4)条件下港内有效波高的对比。由图 12可见,两种组合型港池在边界反射系数减少的情况下,港内波浪的波幅均有不同程度的减小,内部港池在距离最内侧壁面2.0~4.0 m左右时有效波高的减少量达到最大值,总体上内部港池消减效果最好,外部港池因受到内部港池波浪反射和折角地形等影响波况复杂,消减效果较差。

|
图 12 全反射与部分反射边界有效波高差值(单位:cm) Figure 12 Significant wave height difference between total reflection and partial reflective boundary(unit: cm) |
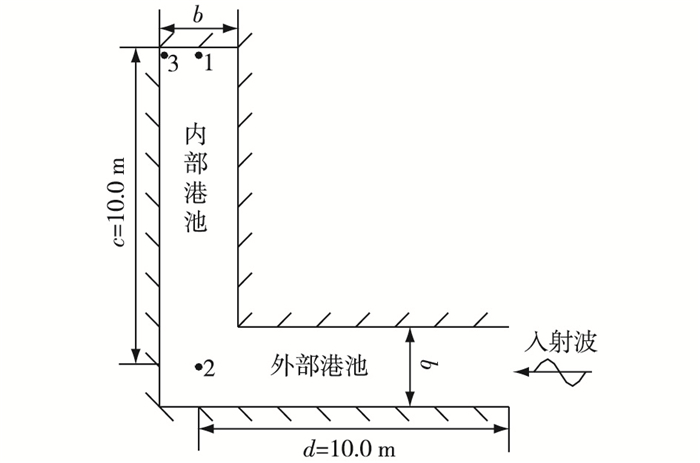
当港湾宽度与长度为同一量级时,港内将会出现明显的横向共振。为了说明港湾内横向共振的波幅空间分布,研究港湾宽度增大对组合型港池港内共振的影响,此处采用3.2节的组合型港池,取内部港池长度c=10.0 m,计算模型和入射波参数设置同前。本节不深入讨论这些横向共振是在何种动力因素诱导下产生的,仅仅讨论港池宽度增大时港内出现横向共振时的运动形态。
模型布置如图 13所示,将港池宽度b逐渐增大,取测点1和测点2做傅里叶变换得到频谱图,各测点的主要共振模态的频率和振幅随港池宽度的变化趋势见图 14。
|
图 13 港内测点布置 Figure 13 Schematic diagram of measuring points in harbor |

|
图 14 港池宽度变化下各测点的共振模态的响应频率和振幅 Figure 14 Response frequency and amplitude of resonance modes at each measurement point under changes in width of harbor |
由图 14可见,在港池宽度不断增大的情况下,港内前两个共振模态的频率始终保持在其固有频率附近,即使宽度b增大到总长度c+d的一半10.0 m时(此时已不满足狭窄港池的假定),前两个共振模态仍稳定存在,其共振频率和细长矩形港池的共振频率吻合依然良好,最大误差不超过5.2%。同时当宽度b从2.0 m开始增大时,前两个共振模态的振幅迅速减小,然后随着b的继续增大,振幅下降的速率逐渐减小,其中第2共振模态因b=10.0 m时在内部港池中形成驻波导致振幅增大。
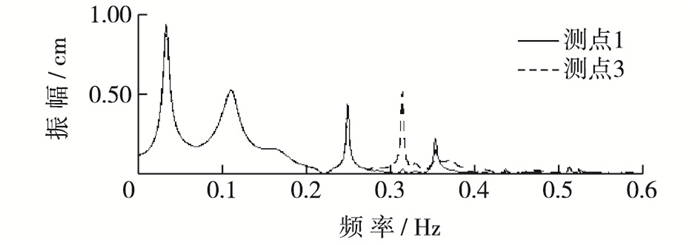
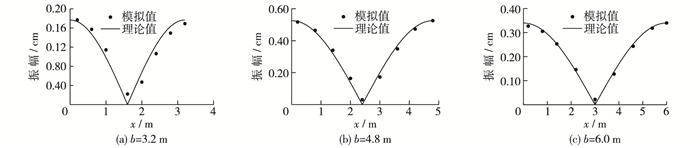
相比于狭窄型港池,宽度增加使港内产生明显的横向共振,港内波况更为复杂,这时有些模态(特别是较高模态)容易被破坏,不能稳定存在。因此与3.2节中港内产生的3个稳定的共振模态不同,本节中港内第3共振模态在宽度b=5.0 m左右时峰值逐渐消失。基于同样的原因,随着宽度的增大,港内必然会激发横向共振,但横向共振的振幅大小随宽度的增大无明显的变化规律。当宽度b=2.0 m时没有明显的横向共振模态的峰值出现,在宽度到达2.4 m时,横向共振模态的振幅大小仅为第1共振模态振幅的7.6%,当宽度继续增大到4.8 m时横向共振模态的振幅为第1共振模态的55%,随后宽度达到6.0 m时,横向共振模态的振幅又减小为第1共振模态的42%。图 15为宽度b=4.8 m时测点1和测点3的频谱图比较,由图 15可见,测点3在频率约为0.314 Hz附近时出现了在测点1处没有的明显峰值,该频率成分即为横向共振模态所对应的频率。从测点3开始沿宽度方向等间距布置8~10个测点,绘出波幅分布与理论对比图,见图 16。由图 16可见,模拟结果与理论值吻合良好。
|
图 15 宽度为4.8 m的组合型港池中测点1和测点3波浪频谱比较 Figure 15 Comparison of wave spectra of measuring points 1 and 3 in combined harbor with a width of 4.8 m |
|
图 16 不同宽度港池中横向共振的波幅分布 Figure 16 Amplitude distribution of transverse resonance in harbors with different widths |
本文采用MIKE 21-BW模块模拟孤立波入射组合型港池的港湾共振现象,通过对模拟结果与现有理论结果的对比可知:
(1) 不同平面布置形式的组合型港池在孤立波入射时,港内激发的最内侧壁面至口门处的响应频率和与其长度相等的细长港池的理论固有频率接近,可以采用细长港池的固有频率估算组合型港池的主要共振频率。
(2) 由于波浪在未到达最内侧壁面之前就发生反射,组合型港池对港湾共振有一定的削弱作用;内部港池的长度越大第1共振模态的振幅越小,第2和第3共振模态的振幅主要受其模态的波长与内外港池长度之间关系的影响,当内部港池长度等于半波长的整数倍时,振幅最大,当外部港池长度等于半波长的整数倍时,振幅最小;内外港池的口门距离并非越小越好,距离越小第2共振模态的振幅越大,第1共振模态的振幅越小,最终第2模态振幅将超过第1共振模态振幅。
(3) 对于本文中的狭长组合型港池,不同波浪入射方向对港内各模态的形成几乎没有影响,但是增大港池宽度会使港内激发明显的横向共振,且横向共振的振幅随宽度的增加没有明显的变化规律。
(4) 由于共振长波不易被消减或吸收,减小边界反射系数对港湾共振的振幅影响不大,但可以较大程度地减小港内有效波高,优化港内的波况。
(5) 设计组合型港池时,内外港池的口门距离不要小于外部港池长度的一半,同时内部港池长度应避免取到最内侧壁面至外海口门距离的2/3,以避免第2共振模态的振幅加强,并尽量减小最内侧港池边界的反射系数,如设置护面块石等。
| [1] |
王岗, 高俊亮, 王培涛, 等. 港湾共振研究综述[J]. 海洋学报, 2017, 39(11): 1-13. ( WANG Gang, GAO Junliang, WANG Peitao, et al. Review on harbor resonance[J]. Acta Oceanologica Sinica, 2017, 39(11): 1-13. DOI:10.3969/j.issn.0253-4193.2017.11.001 (in Chinese)) |
| [2] |
MCNOWN J S. Waves and seiche in idealized ports[C]//National Bureau of Standards. Gravity Waves Symposium, 1952: 153-164.
|
| [3] |
MILES J, MUNK W. Harbor paradox[J]. Journal of the Waterways and Harbors Division, 1961, 87(3): 111-132. |
| [4] |
IPPEN A T, GODA Y. Wave induced oscillations in harbors: the solution for a rectangular harbor connected to the open sea[R]. Hydrodynamics Laboratory, Massachusettes Institute of Technology, 1963.
|
| [5] |
LEE J J. Wave-induced oscillations in harbours of arbitrary geometry[J]. Journal of Fluid Mechanics, 1971, 45(2): 375-394. DOI:10.1017/S0022112071000090 |
| [6] |
NWOGU O G. Time domain simulation of long period oscillations in harbors[C]//International Conference on Coastal Engineering. 2001: 3643-3654.
|
| [7] |
DONG G H, GANG W, MA X Z, et al. Numerical study of transient nonlinear harbor resonance[J]. Science China(Technological Sciences), 2010, 53(2): 558-565. DOI:10.1007/s11431-009-0409-5 |
| [8] |
马小舟, 刘嫔, 王岗, 等. 孤立波作用下细长港响应的数值研究[J]. 计算力学学报, 2013, 30(1): 101-105. ( MA Xiaozhou, LIU Pin, WANG Gang, et al. Numerical study on the response of a narrow-long harbor to a solitary wave[J]. Chinese Journal of Computational Mechanics, 2013, 30(1): 101-105. (in Chinese)) |
| [9] |
刘嫔.港口自振频率的研究[D].大连: 大连理工大学, 2012. (LIU Pin. Study on the natural frequency of harbor[D]. Dalian: Dalian University of Technology, 2012. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394316.htm
|
| [10] |
史宏达, 徐国栋, 孙龙龙. 矩形港池的港内共振研究[J]. 海岸工程, 2011, 30(2): 14-21. ( SHI Hongda, XU Guodong, SUN Longlong. Study on resonance in a rectangular harbor basin[J]. Coastal Engineering, 2011, 30(2): 14-21. DOI:10.3969/j.issn.1002-3682.2011.02.003 (in Chinese)) |
| [11] |
郑金海, 董文凯, 徐龙辉, 等. 矩形及其扩展形状港湾内的水波共振[J]. 计算力学学报, 2014(2): 254-258. ( ZHENG Jinhai, DONG Wenkai, XU Longhui, et al. Water-wave resonance within a rectangular harbor and its extensional shapes[J]. Chinese Journal of Computational Mechanics, 2014(2): 254-258. (in Chinese)) |
| [12] |
高俊亮, 马小舟, 董国海, 等. 港湾振荡下港内低频波浪的数值研究[J]. 工程力学, 2016, 33(7): 159-166. ( GAO Junliang, MA Xiaozhou, DONG Guohai, et al. Numerical study on low-frequency waves inside the harbor during harbor oscillations[J]. Engineering Mechanics, 2016, 33(7): 159-166. (in Chinese)) |
| [13] |
GAO J, JI C, GAIDAI O, et al. Numerical study of infragravity waves amplification during harbor resonance[J]. Ocean Engineering, 2016, 116: 90-100. DOI:10.1016/j.oceaneng.2016.02.032 |
| [14] |
高俊亮, 嵇春艳, 郑子波, 等. N波诱发的瞬变港湾振荡的数值研究[J]. 哈尔滨工程大学学报, 2017, 38(8): 1203-1209. ( GAO Junliang, JI Chunyan, ZHENG Zibo, et al. Numerical study on transient harbor oscillations induced by N-waves[J]. Journal of Harbin Engineering University, 2017, 38(8): 1203-1209. (in Chinese)) |
| [15] |
GAO J, JI C, GAIDAI O, et al. Numerical investigation of transient harbor oscillations induced by N-waves[J]. Coastal Engineering, 2017, 230(1): 119-131. |
| [16] |
MEI C C. The applied dynamics of ocean surface waves[J]. Ocean Engineering, 1984, 11(3): 321. DOI:10.1016/0029-8018(84)90033-7 |
| [17] |
邹志利. 水波理论及其应用[M]. 北京: 科学出版社, 2005. ( ZOU Zhili. Water wave theories and their applications[M]. Beijing: Science Press, 2005. (in Chinese))
|
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2018
2018 