2. 天津大学岩土工程研究所,天津 300072
钻井船是海洋石油开采工程中的重要工具。自升式钻井船工作时依靠桩靴贯入海床中提供竖向支撑力和水平抵抗力,桩靴贯入及拔出过程中会排开大量土体,对周围土体扰动特别大。然而钻井船工作时附近可能有海洋桩平台,钻井船桩靴贯入及拔出产生的土体位移会挤压桩基础,使桩挠曲、倾斜甚至失稳,对临近桩平台产生不利影响。因此有必要对钻井船桩靴在不同场地中贯入及拔出对邻近桩的影响进行研究。
针对钻井船插拔桩对邻近桩的影响,国内外学者开展了一些研究。Siciliano等[1]针对钻井船在正常固结软黏土场地插桩问题进行了100g条件下的离心模型试验,分析了不同桩靴与邻近桩间距时桩靴贯入对邻近桩的影响,并通过梁-柱模型建立邻近桩与周围土体的相互作用关系,根据桩身弯矩对桩靴贯入产生的土体位移进行了反分析。Craig[2]针对钻井船在黏土上覆盖砂土场地中的插桩问题也进行了100g条件下的离心模型试验,分析插桩过程对邻近桩水平承载力的影响。Stewart [3]针对自升式钻井平台插拔桩后邻近桩受到横向荷载的情况,分析不同强度黏土中桩靴贯入过程对邻近桩水平承载特性产生的影响,为研究不同强度土层中的桩身响应提供参考依据。以上工作虽然对黏土场地中插、拔桩靴对邻近桩的影响进行了一定研究,但没有研究桩靴对周围土体的影响。Xie[4]在软黏土场地和砂土上覆盖黏土的场地中进行100g条件下的离心模型试验,利用PIV技术揭示了周围土体变形机理。田兆丰[5]通过实验室自行研发的土体位移测量装置测得特定位置处土体位移也为两段法计算提供试验数据。以上研究大部分是关于黏土场地和黏土上方或下方铺设砂土的场地中插拔桩对邻近桩影响的研究。吴永韧等[6]通过1 g条件下的模型试验,分析了饱和粉砂地基中桩靴贯入对临近平台桩基础的影响;尽管他对粉砂场地中桩靴贯入对邻近桩的影响进行研究分析,但对邻近桩响应的介绍较少。
综上所述,目前钻井船插拔桩对邻近桩影响的研究主要针对某单一土层场地或者混合成层土场地进行研究,虽然对于不同场地插拔桩对邻近桩的影响已有了一定认识,但仍然缺少系统的比较和研究。针对上述问题本文分别在黏土和砂土场地中进行了插、拔桩试验,分析研究不同场地中钻井船插桩对邻近桩的影响,以及不同工作场地中钻井船插、拔桩阻力对邻近桩影响的规律。
1 模型试验概况模型试验具体过程:①制备试验土体,并安装邻近桩及土体位移测量装置;②测量试验土体土性参数;③试验中保持桩靴贯入速率为0.1 mm/s,贯入到预定位置为止(黏土场地中桩靴贯入深度dc=0.45 m,砂土场地中桩靴贯入深度ds=0.15 m);④切换伺服加载装置,对桩靴施加恒定的力,模拟钻井船工作过程;⑤拔桩过程中桩靴上拔速度为0.1 mm/s,桩靴拔出泥面后停止。
1.1 模型参数及土层模型试验桩靴原型直径Dp=18 m,为减小边界效应的影响,使试验结果更加准确,确定模型试验尺寸相似比N=100,即模型桩靴直径D=18 cm。桩基础竖向承载力主要由桩端阻力(端承桩)和桩身摩擦阻力(摩擦桩)两方面提供,为增加摩擦阻力一般加长桩基础,按照相对刚度分类,属于柔性桩[7],根据邻近桩模型的尺寸形状,选用铝合金圆管,邻近桩模型具体参数为内径10.0 mm,外径12.3 mm,桩长1.1 m,弹性模量为70 GPa,截面惯性矩526.7 mm4。邻近桩模型入土0.9 m,沿桩身布置9对应变片测量桩身弯矩,1号应变片布置在距离桩尖0.1 m处,9号应变片在土面处, 两对应变片之间间隔0.1 m。
土体位移测量装置由实验室自行设计制作,装置共10段,底端固定,中间8段为测量单元,顶端是信号集成端及接口。试验所用场地土体厚0.9 m,具体物理力学参数指标见表 1。
| 表 1 场地土体物理力学参数指标 Table 1 Parameter index of physical and mechanical properties of clay |
用分层击实法现场制备砂土土层。土层厚0.9 m,每层0.1 m,分9层填装砂土,每层划分均匀的7块,每块装土190 kg,每层装土完成后将土整平,用击实锤击实达到预定厚度。
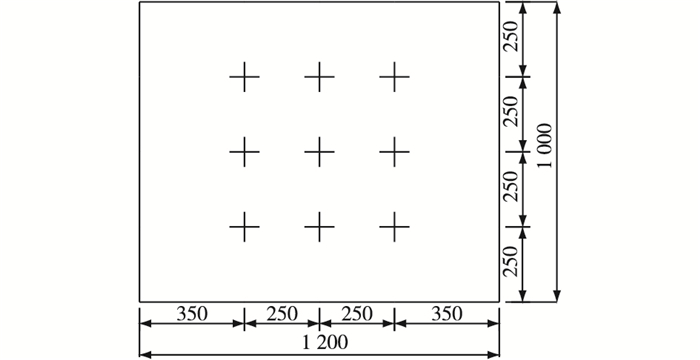
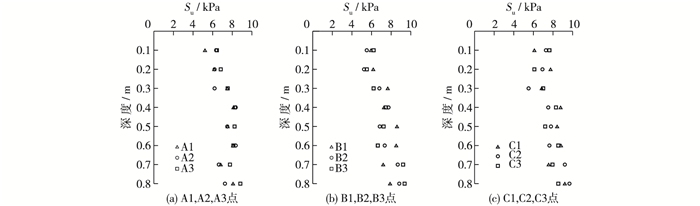
对黏土场地进行电动十字板剪切试验,测点位置如图 1所示。测试结果(图 2)表明,该试验土层不排水抗剪强度随土体深度略有增加,土体抗剪强度随土体深度变化的拟合函数为:
| $ {S_{\text{u}}} = 5.8 + 2.75{d_1} $ | (1) |
|
图 1 电动十字板剪切试验测点(单位:mm) Figure 1 Testing points for monitoring undrained shear strength (unit: mm) |
|
图 2 不同位置测点处不排水抗剪强 Figure 2 Undrained shear strength of different monitoring points |
式中:Su为土体不排水抗剪强度(kPa);d1为土体深度(m)。
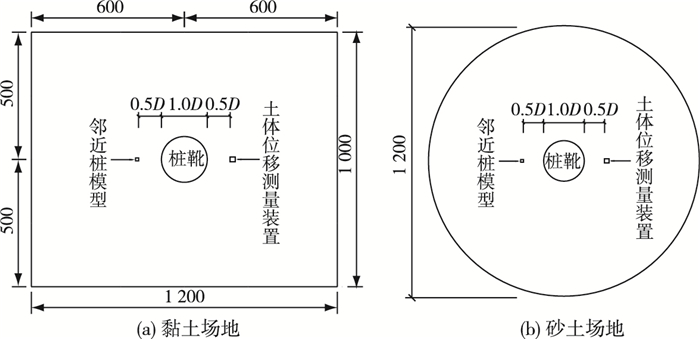
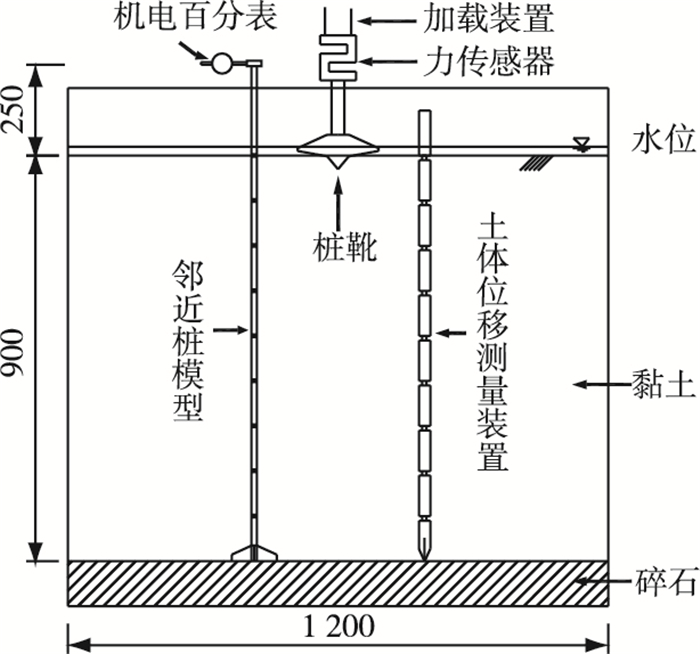
1.2 试验布置试验过程中邻近桩桩头完全自由,即不约束桩头的位移和转角。在距离邻近桩0.5D(D表示桩靴直径,本试验的桩靴直径为18 cm)位置以0.1 mm/s速度进行插桩和拔桩。邻近桩及土体位移测量装置分别安装在桩靴两侧,距离桩靴边缘0.5D(见图 3和4)。伺服电动缸通过反力架与模型箱相连,并由它带动桩靴以0.1 mm/s的速度贯入及拔出,为了测量桩靴贯入阻力及拔出抗力,桩靴与电动缸推杆之间由力传感器连接。为准确测量桩靴在土体以下的深度,安装1个55 cm量程的位移传感器。在桩的研究中,桩头位移十分重要,可以简化认为是桩身位移的外在表现,所以桩头处需要通过机电百分表测量桩头位移。
|
图 3 试验平面布置(单位:mm) Figure 3 Plan layout of model tests (unit: mm) |
|
图 4 试验设备剖面(单位:mm) Figure 4 Profile of model tests (unit: mm) |
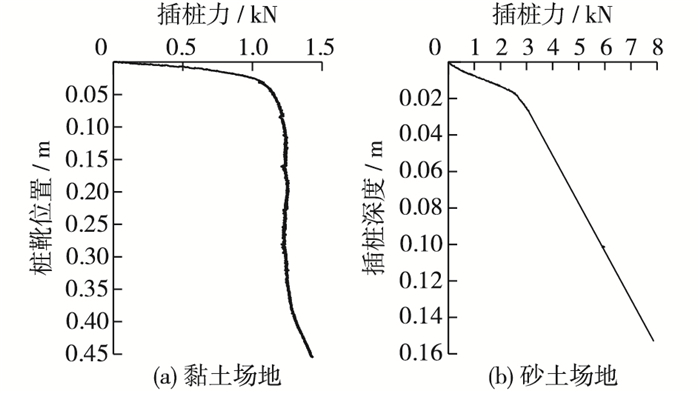
图 5为桩靴贯入阻力随插桩深度变化曲线。试验结果表明,在黏土场地桩靴贯入过程中,当桩靴贯入0.1 m深(约为0.5D)后插桩阻力基本稳定,最大插桩阻力和桩靴尺寸与黏土的物性指标密切相关;而在砂土场地桩靴贯入过程中,桩靴贯入阻力曲线是一条光滑的折线,转折点在0.02 m深度处(约为0.1D),两条直线的不同斜率表示插桩阻力不同的变化速率,转折点之前的插桩阻力变化速率较小,转折点之后的插桩阻力变化速率较大。砂土场地的桩靴贯入阻力整体上随深度呈线性增大。
|
图 5 桩靴贯入阻力 Figure 5 Resistance of spudcan penetration |
SNAME认为插桩阻力可以看成是土体竖向极限承载力考虑土体回淤和桩靴替换部分土体[8]。从试验现象中发现,砂土场地中贯入桩靴,插桩坑出现部分回淤,回淤土体的深度约为插桩坑高度的一半。砂土场地的最大桩靴贯入阻力计算式为:
| $ F = {F_{\text{V}}}-{{F'}_0}A + \gamma 'V $ | (2) |
| $ {F_{\text{V}}} = \left( {0.5\gamma 'B{N_\gamma }{s_\gamma }{d_\gamma } + {{p'}_0}{N_{\text{q}}}{s_{\text{q}}}{d_{\text{q}}}} \right)A $ | (3) |
式中:FV为极限竖向承载力(kN);F′0为回淤土体上覆有效压力(kPa);V为桩靴体积(m3);γ′为土体有效重度(kN/m3);B为桩靴宽度,圆形桩靴的直径(m);A为桩靴面积(m2);p′0为桩靴最大直径处的上覆有效压力(kPa);Nγ和Nq为强度影响系数,Nγ=2(Nq+1)tanϕ,ϕ为砂土内摩擦角,Nq=eπ tanϕtan2(45°+ϕ/2);sγ和sq为形状影响系数,sγ=1-0.4(B/L),圆形桩靴取值0.6;sq=1+(B/L)tanϕ;dγ和dq为深度影响系数,dγ取值为1,当D/B≤1时,dq=1+2tanϕ(1-sinϕ)2D/B;当D/B>1时,dq=1+2tanϕ(1-sinϕ)2arctan(D/B)。
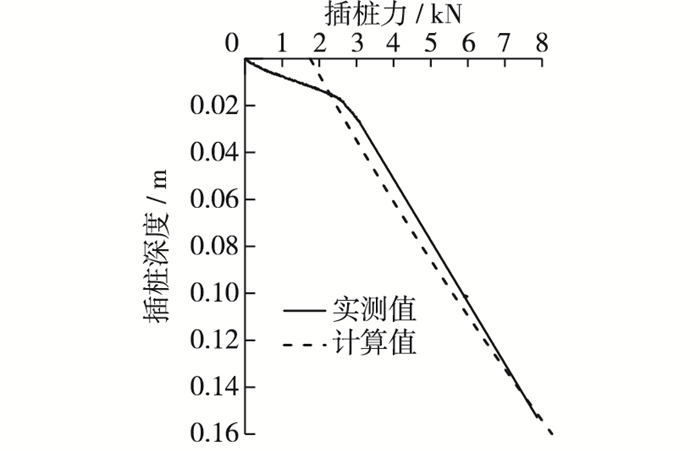
图 6是桩靴贯入阻力实测值和由式(2)得到的计算值随插桩深度变化的曲线。从图 6可见,桩靴贯入阻力变化曲线存在一个转折点,转折点以前桩靴贯入阻力变化速率较慢,转折点以后桩靴贯入阻力变化速率较快,这与SNAME计算式(2)得到的结果基本一致。
|
图 6 砂土场地桩靴贯入阻力实测值和计算值 Figure 6 Measured and calculated values of penetration resistance of spudcan in sand |
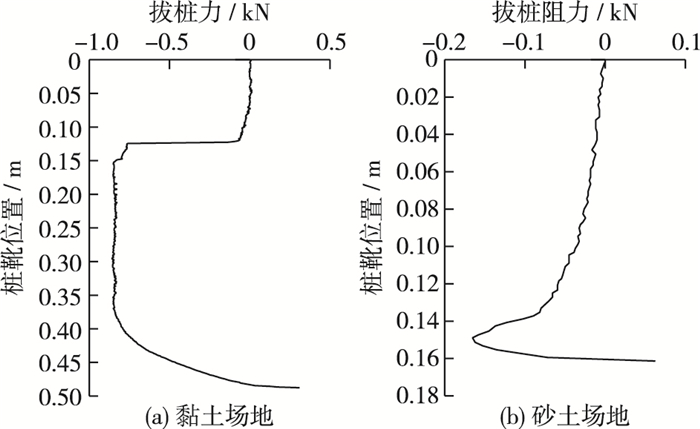
图 7是拔桩阻力随拔桩深度变化的曲线。从图 7可见,黏土场地拔桩在初始阶段拔桩力迅速增加,当桩靴拔出1D后拔桩阻力基本稳定,当桩靴距离土面0.12 m处,拔桩阻力迅速变小并趋于零,从试验中可以看出,此时桩靴和土完全分离;砂土场地中拔桩阻力初始阶段会迅速增大,达到峰值后又迅速减小,当减小到一定程度后变化速率减缓。和黏土场地的拔桩相比较,砂土场地中拔桩阻力在初期变化最剧烈,后期较为稳定;而黏土场地的拔桩过程则相反。
|
图 7 桩靴拔出阻力 Figure 7 Resistance of spudcan extraction in clay and sand |
Purwana[9]对黏土场地中拔桩的研究表明,拔桩阻力有很大一部分由桩底吸力贡献。分析拔桩阻力的变化,表明在该拔桩速率下,桩靴底部所能提供的吸附力及桩周土提供的摩擦力的合力是一个由小到大随后突降为0的过程,其中桩靴底部和土体之间的吸力起主导作用。
砂土场地中的拔桩阻力曲线在初期(桩靴从0.16 m到0.15 m)增长迅速,达到峰值;在中期(桩靴从0.15 m到0.13 m)迅速减小,减到峰值的50%;在后期(桩靴从0.13 m到完全拔出过程)基本保持线性减少趋势,直至减小到零。
Meyerhof和Adams在试验中发现砂土场地中拔桩的土体破坏面呈圆台形状,将此破坏面简化为圆柱形滑动剪切面,通过竖向剪切面土压力影响系数Ku将两者联系起来, 并提出一个半经验式计算拔桩极限承载力Pu[10]。
| $ {P_{\text{u}}} = W + \pi Dcl + \frac{\pi }{2}{S_{\text{r}}}D\gamma '{l^2}{K_{\text{u}}}\tan \phi, \;\;\;L \leqslant H $ | (4) |
| $ {P_{\text{u}}} = W + \pi Dcl + \frac{\pi }{2}{S_{\text{r}}}D\gamma '\left( {2l-H} \right)H{K_{\text{u}}}\tan \phi, L > H $ | (5) |
式中:W为桩靴上部土体重量,W=πDγl; Ku为竖向剪切面土压力影响系数,Ku=0.496ϕ;Sr为被动土压力形状影响系数,Sr=1+ml/D,系数m在表 2中选取。
| 表 2 系数m参考值 Table 2 Reference values of m |
Meyerhof-Adams经验式在初始时刻认为桩靴上部泥面齐平,与试验过程中拔桩初始状态吻合,通过Meyerhof-Adams法计算得到桩靴上拔阻力的理论值(见图 8)。从图 8可见,当砂土内摩擦角按照试验前的参数取41°时计算得到的值比实测值偏大,当内摩擦角取25°时,理论值和实测值吻合较好。这可能是由于该部分土体是周围土体回淤后产生的,相比试验前制备的密实土体,这部分土体是松散的。经过扰动,土体发生了弱化,其物性参数发生改变。桩靴在0.14 ~0.16 m位置时,桩靴上拔阻力实测值明显大于理论值,此时应该存在其他的影响因素,例如桩靴与下部土体的黏聚力,针对此问题没有开展进一步研究。

|
图 8 砂土场地桩靴上拔阻力计算值和实测值 Figure 8 Measured and calculated values of resistance of spudcan extraction in sand |
对比黏土场地和砂土场地中的插、拔桩阻力发现:①插桩过程中,在两种不同场地桩靴贯入相同深度时,桩靴贯入阻力值的大小相差悬殊,在桩靴贯入0.15 m深时,黏土场地的桩靴贯入阻力是砂土场地的16.4%,因此桩靴在不同场地中的相同深度,砂土场地可以提供更大的承载力;②拔桩过程中,在黏土场地的拔桩阻力最大值是砂土场地的5倍,因此砂土场地中拔桩可以较为轻松地完成,而在黏土场地中需要更加详细的论证和研究;③黏土场地中拔桩阻力最大值是插桩阻力最大值的66.5%,砂土场地中拔桩阻力最大值是插桩阻力最大值的2.1%。
2.2 土体位移桩靴直接作用于土体,插、拔桩过程中对周围土体扰动非常剧烈,造成土体水平方向的移动。试验过程中发现,桩靴贯入过程中,黏土土体回淤不明显,砂土土体出现部分回淤,模型桩靴被砂土覆盖;桩靴拔出过程中,黏土土体部分回淤,砂土土体回淤明显,插桩坑基本不可见。图 9和10分别给出了插桩和拔桩过程中距离桩靴边缘0.5D处的黏土及砂土土体水平位移场。

|
图 9 黏土场地中土体水平位移 Figure 9 Horizontal displacement of soil mass in clay |
|
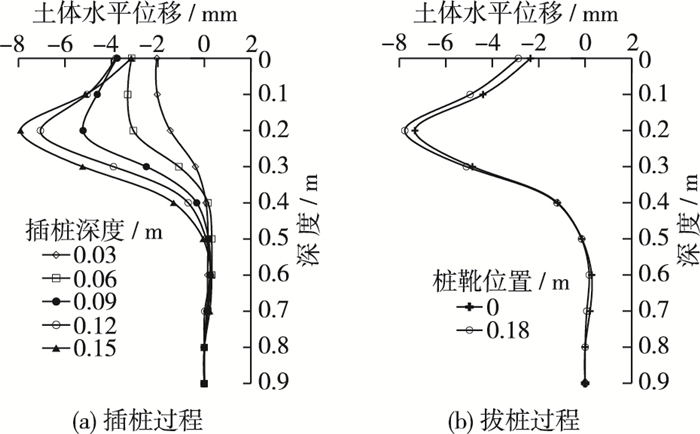
图 10 砂土场地中土体水平位移 Figure 10 Horizontal displacement of soil mass in sand |
图 9(a)和图 10(a)是桩靴贯入过程中邻近桩周围土体的水平运动,从图中可以看出,桩靴贯入造成桩靴周围土体向远离桩靴的方向运动,随着桩靴向下贯入,发生最大土体水平位移处逐渐下移,且发生在桩靴水平位置深度处;桩靴水平位置以上的土体表现为运动减缓、停滞甚至回淤的现象,此时土体处于卸载状态。图 9(b)和图 10(b)显示的是桩靴拔出过程中邻近桩周围土体的水平运动,从图中可以看出,桩靴拔出使邻近桩附近土体向桩靴方向运动,虽然拔桩过程初始条件不同,但是可以看出桩靴从0.15 m上拔至泥面处,黏土土体运动变化更为明显。
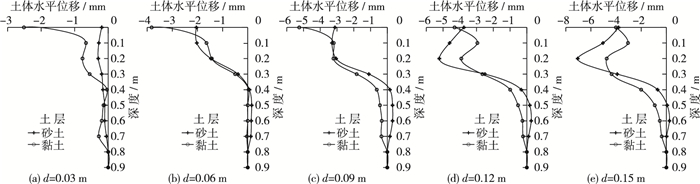
图 11是桩靴贯入深度0 ≤d≤0.15 m过程中土体水平位移在各个时刻的比较。由图可知,在泥面处的土体位移非常相似,基本为2~5 mm,但随着深度加深,变化规律表现不同。在黏土场地中当插桩深度小于0.1 m时,最大土体位移发生在泥面处,当插桩深度大于0.1 m时,最大土体位移发生在桩靴水平位置处;而在砂土场地中,最大土体位移基本发生在桩靴水平位置处。比较桩靴贯入0.15 m时刻的土体水平位移,发现砂土场地的最大土体水平位移比黏土场地的最大土体水平位移大,约是黏土场地的1.6倍,说明桩靴贯入在砂土场地的水平方向上影响较大;在桩靴贯入深度0 ≤d≤0.15 m过程中,砂土场地0.5 m深度以下土体基本没有发生变化,而在黏土场地则发生了更加明显的变化,特别是d=0.12 m及以后的过程,由此可见桩靴贯入在黏土场地的垂直方向上影响大。
|
图 11 插桩过程中土体水平位移(0≤d≤0.15 m) Figure 11 Horizontal displacement of soil mass during spudcan penetration (0≤d≤0.15 m) |
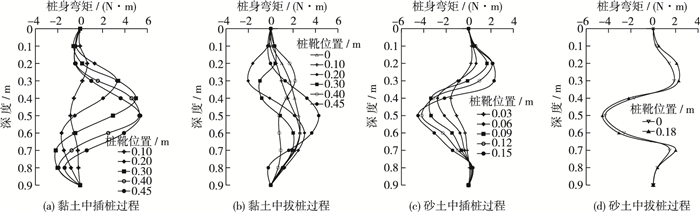
土体运动会挤压邻近桩,使邻近桩受力产生弯曲和移动,从而影响邻近桩的安全。图 12给出了插、拔桩过程中的桩身弯矩分布,规定桩靴一侧受拉为正受压为负。从图 12可以看出,插桩初期,沿桩身都是负弯矩,表示桩靴一侧受拉,此时桩靴排开泥面处土体,土体挤压邻近桩上部,使邻近桩向远离桩靴的方向弯曲。随着桩靴贯入深度增加,负弯矩最大处逐渐下移,并且数值逐渐增大,上部逐渐出现正弯矩,正弯矩的发展趋势和负弯矩基本相同,最大弯矩处逐渐下移,且数值逐渐增大。拔桩过程中,黏土场地中桩身弯矩变化比较明显,最大桩身弯矩减小,0.5 m(拔桩初始时刻桩靴位置)以下桩身弯矩随着桩靴上拔逐渐减小,此时土体受桩身拔出影响产生回淤,土体对邻近桩卸载;砂土场地中桩身弯矩变化不明显,从初始时刻和结束时刻可以看出桩身弯矩减小。
|
图 12 黏土和砂土场地中桩身弯矩 Figure 12 Bending moment of pile shaft during spudcan penetration and extraction in clay and sand |
黏土场地中最大负弯矩是最大正弯矩的75%,砂土场地中的最大负弯矩是最大正弯矩的2倍。上文中已经证明插桩对砂土场地有很大扰动,使上部土体弱化,因此在砂土场地中插桩时,桩靴上部土体弱化,对邻近桩的支持力减弱,下部土体被挤密增强了邻近桩的水平承载力,与文献[11-13]的研究结果一致。此时出现负弯矩大于正弯矩的现象,在黏土场地中没有这种现象。
在同一种场地中,桩身最大弯矩发生在桩靴贯入阶段,分析插桩过程中桩身最大弯矩发生的时刻,并预测桩身最大弯矩随桩靴贯入的变化规律(图 13)。从图 13可见,两种场地中最大桩身弯矩均随桩靴贯入深度增加逐渐增大,并且在桩靴贯入0.3 m深(约1.67D)后,最大桩身弯矩变化减缓甚至基本保持不变,此时桩达到最危险状态。

|
图 13 最大桩身弯矩 Figure 13 Mmaximum bending moment of pile along with depth of spudcan penetration |
图 14给出了钻井船插桩过程中的桩头水平位移。从图 14可见,砂土场地中插桩造成的桩头水平位移明显大于黏土场地,前者约为后者的3.7倍。此时桩尖位置不变,砂土场地中的邻近单桩比黏土场地的更加倾斜,也更不利于邻近桩平台的安全使用。另外,当桩靴贯入0.09 m(0.5D)深时,桩头水平位移基本达到最大值,之后开始缓慢减小;而砂土场地的桩头水平位移曲线开始时增速较快,然后逐渐减缓,最后基本趋于平稳。

|
图 14 桩头水平位移 Figure 14 Horizontal displacement of pile head |
(1) 桩靴贯入相同深度,砂土场地可以提供更大承载力;拔桩过程中,黏土场地更加难以拔出,需要较大拔桩力。砂土是钻井船工作的最佳场地。
(2) 在软黏土场地中插桩,桩靴对土体强度影响较小;在密实砂土场地中,桩靴使其上部土体软化,强度减小。
(3) 桩靴对土体的影响方向存在差异,桩靴贯入在砂土场地的水平方向上影响较广,在黏土场地的垂直方向上影响更深。
(4) 插桩相同深度,在黏土场地中最大弯矩发生在桩靴最大直径处,而在砂土场地中发生在邻近桩下部,最大桩身弯矩随着插桩深度增大而增加,但是当桩靴贯入到一定深度后,最大桩身弯矩基本保持不变。
(5) 桩靴贯入过程中,桩头位移在黏土场地中的数值较小,并且在远离桩靴达到最大值后又逐渐减小,有向桩靴方向移动的趋势;而在砂土场地中数值较大,在远离桩靴方向上逐渐增大,然后基本稳定。
| [1] |
SICILIANO R J, HAMILTON J M, MURFF J D, et al. Effect of jack-up spudcans on piles[J]. Offshore Technology Conference, 1990, OTC 6467. |
| [2] |
CRAIG W H. Spud-can foundations: Installation with deep penetration and subsequent removal[J]. Proceedings of the ICE-Geotechnical Engineering, 1998, 131(3): 146-151. DOI:10.1680/igeng.1998.30470 |
| [3] |
STEWART D P. Influence of jack-up operation adjacent to a piled structure[J]. Proceeding International Symposium Frontiers in Offshore Geotechnics, 2005, 543-549. |
| [4] |
XIE Y. Centrifuge model study on spudcan-pile interaction[D]. Singapore: National University of Singapore, 2009.
|
| [5] |
田兆丰.钻井船插、拔桩对邻近桩影响的模型试验[D].天津: 天津大学, 2017. (TIAN Zhaofeng. Model tests on effects of spudcan penetration and extraction on adjacent piles[D]. Tianjin: Tianjin University, 2017. (in Chinese))
|
| [6] |
吴永韧, 鲁晓兵, 王淑云, 等. Spudcan基础贯入对固定平台基础影响[J]. 中国海洋平台, 2008, 23(1): 35-38. ( WU Yongren, LU Xiaobing, WANG Shuyun, et al. Effects of spud-can on pile foundation of fixed platform[J]. China Offshore Platform, 2008, 23(1): 35-38. DOI:10.3969/j.issn.1001-4500.2008.01.007 (in Chinese)) |
| [7] |
JTJ 254—98港口工程桩基规范[S]. (JTJ 254—98 Code for pile foundation in port engineering[S]. (in Chinese))
|
| [8] |
SNAME. Recommended practice for site specific assessment of mobile jack-up units[S]. Society of Naval Architects and Marine Engineers. Technical and Research Bulletin 5-5A. New Jersey, 2007.
|
| [9] |
PURWANA O A. Centrifuge model study on spudcan extraction in soft clay[D]. Singapore: National University of Singapore, 2007.
|
| [10] |
MEYERHOF G G, ADAMS J I. The ultimate uplift capacity of foundations[J]. Canadian Geotechnical Journal, 1968, 5(4): 225-244. DOI:10.1139/t68-024 |
| [11] |
张其一. 自升式平台桩基土体变形规律与破坏机理分析[J]. 中国海洋大学学报, 2012, 42(11): 111-116. ( ZHANG Qiyi. Analysis of deformation law and failure mechanism of pile foundation of jack-up platform[J]. Periodical of Ocean University of China, 2012, 42(11): 111-116. (in Chinese)) |
| [12] |
陶常飞.曹妃甸浅滩海洋工程地质特征及插桩深度研究[D].青岛: 中国海洋大学, 2008. (TAO Changfei. Reasearch on the characteristics of marine engineering geology and the depth of pile penetration in Caofeidian Shoal[D]. Qingdao: Ocean University of China, 2008. (in Chinese))
|
| [13] |
王琦. 自升式平台插桩物理模型试验及分析[J]. 中国水运, 2014, 14(3): 364-366. ( WANG Qi. Model test and analysis of jack-up platform penetration[J]. China Water Transport, 2014, 14(3): 364-366. (in Chinese)) |
2. Geotechnical Engineering Institute, Tianjin University, Tianjin 300072, China
 2018
2018 
