在实际工程中,绝大多数的岩土工程问题属于或者部分属于非饱和土的范畴,研究非饱和土的首要问题是研究非饱和土的土-水特征曲线,因为它能很好地反映非饱和土的工程力学特性。而在土-水特征曲线的研究进程中,各种影响因素下土-水特征曲线(SWCC)的变化规律是研究的重点之一[1]。土-水特征曲线是非饱和土力学中的基础本构关系,描述了土体吸力与土体含水率之间的关系[2-3]。非饱和土体吸力包括总吸力与基质吸力,土体的含水率包含质量含水率、体积含水率及饱和度。许多学者[4-9]研究发现影响土-水特征曲线的因素包含土的矿物成分、土颗粒的粒径和级配、初始干密度、应力历史、干湿循环等,并且这些因素对非饱和土基质吸力的影响十分复杂。如陈东霞等[4]通过滤纸法试验探讨了初始含水率、干密度、竖向应力及干湿循环对土-水特征曲线中脱湿曲线的影响;文宝萍等[5]根据颗粒级配和土-水特征曲线各参数间的定量关系研究土样颗粒级配对非饱和土基本特性的影响程度。对于应力状态、温度、干湿循环、矿物成分和干密度对非饱和土基质吸力的影响已有学者进行了不同程度的研究[1, 7-11]。如赵天宇等[7]通过Ku-pF非饱和导水仪和压力膜仪分别测量了不同干密度和不同干湿循环状态下重塑黄土的土-水特征曲线,并得到进气值及残余含水率等;王铁行等[8]通过对扰动黄土进行研究,测得了不同密度及温度对黄土土-水特征曲线的影响。通过对上述文献的研究发现单纯分析颗粒级配对非饱和土土-水特征曲线的影响研究成果很少,本文着重对此进行分析研究。
许多研究[12-13]表明在分形理论中,土体分维数D会随细颗粒土含量增加而增加,即细土颗粒含量与分维数D之间存在相关性。因此本文以江西红土为研究对象,配制不同颗粒级配的试样,并用滤纸法测量基质吸力,得到土-水特征曲线,然后推算出各土-水特征曲线的特征值,运用土粒累计质量-粒径分布的分形模型[14-15],通过分形理论中分维数D指标描述粒组中细颗粒含量的增加与减少,讨论分维数D与土-水特征曲线各个特征值的关系,用以表征不同颗粒粒径含量的增减所反映出的土-水特征曲线变化规律。
1 试验材料 1.1 试验用土基本物理指标所用土样为江西南昌市瑶湖地区某新建道路的路基填筑用土。该土样呈红褐色,密度为2.75 g/cm3,液限为32.5%,塑限为26.7%,塑性指数为9.8,根据《建筑地基基础设计规范》将试验用土定名为粉土,其最大干密度为1.88 g/cm3, 最优含水率为15%。
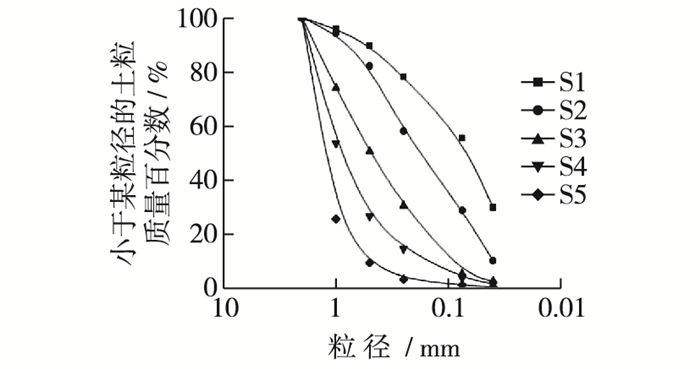
1.2 土样制备为了研究土-水特征曲线与颗粒级配的定量关系,采用筛分的方法,人工配制了5组不同颗粒级配的试样。将试验用土过2.0 mm筛,进行烘干备用,然后分别过1.0, 0.5, 0.25和0.074 mm筛,再用密度计法测得粒径小于0.074 mm的含量,最后把过筛后的土配制成颗粒粒径含量不同的土样。配制土样颗粒级配曲线如图 1所示,土样依次编号为S1,S2,S3,S4,S5。其中S3为试验用土的原始级配土样,S1土样为细粒含量最高、粗粒土含量最少的土样,而S5为细粒含量最少、粗粒土含量最高的土样。
|
图 1 人工配制粒径累积曲线 Figure 1 Particle-size accumulation curves of manual sample |
滤纸法可通过接触式滤纸技术测得土样的基质吸力,通过非接触式滤纸技术测得土样的总吸力。在滤纸和土样接触条件下,由于土内的溶解盐将随液态水一起迁移至滤纸内而不体现渗透吸力的影响,因此接触式仅能反映土体内基质吸力的作用效果。在非接触式条件下,土体和滤纸中的水分是以气态形式相互迁移的,在土体总吸力的吸湿作用下,滤纸平衡含水率、容器内相对湿度和土体总吸力值呈一一对应关系,因此非接触滤纸法可以反映总吸力的作用效果。接触式和非接触式滤纸技术均是确定非饱和土吸力的间接方法,即通过测量从非饱和土样向初始干燥滤纸转移的水量,在已知的率定曲线中可以间接确定土样的吸力值。本文仅研究接触式滤纸技术所测得的基质吸力。
2.2 滤纸法试验步骤将配制好的土样分别制成质量含水率为4.16%,6.38%,9.27%,11.45%,13.57%,16.08%,17.97%,20.08%和22.05%的湿土,再分别放到密封袋内静置2~3 d,使试样中水与土充分接触、混合均匀,防止出现团聚结构,然后将散状土用静压法压制成干密度为1.63 g/cm3的环刀试样,每种含水率都制作2个直径6.18 cm,高度2 cm的土饼。在同一含水率下的两土饼中间放置3层滤纸(滤纸使用前要进行烘干)用以测取基质吸力(上下两层为保护滤纸,直径为6.0 cm,中间为测量滤纸,直径为5.5 cm)。然后将试样放置到铝盒中并用胶带缠绕密封,再把密封好的铝盒放入恒温水槽中静置10 d等待平衡,试验期间保持室内恒温为25 ℃。待平衡时间结束,将铝盒打开取出上层土样,然后用镊子夹取接触式滤纸放到天秤(精度为0.000 1 g)称其质量。为保证测量准确性,这一过程要两人一起协同进行并在30 s内完成。然后再根据滤纸的干湿质量之差,即可算出滤纸的平衡含水率。
试验所用滤纸为杭州新华造纸厂所生产的“双圈”牌No.203型慢速滤纸,技术指标:直径70 cm,灰分0.000 035 g/张,占质量百分比0.01%。其基质吸力率定曲线方程[16-18]为:
| $ \left. \begin{array}{l} \lg S = - 0.076{\omega _{{\rm{fp}}}} + 5.493, {\omega _{{\rm{fp}}}} \le 47\% \\ \lg S = - 0.012{\omega _{{\rm{fp}}}} + 2.470, {\omega _{{\rm{fp}}}} > 47\% \end{array} \right\} $ | (1) |
式中:S为吸力(kPa);ωfp为滤纸的含水率(%)。
根据上述试验方法可以得出基质吸力与体积含水率间的关系曲线,如图 2所示。

|
图 2 不同颗粒粒径含量下土-水特征曲线 Figure 2 Soil-water characteristic curves with different particle size distributions |
土-水特征曲线清晰描述了基质吸力与体积含水率的关系,从图 2可看到在同一体积含水率下细颗粒含量越多的土样基质吸力就越大,其原因是土样中细颗粒多,比表面积增大,对水分子产生的吸附交换能力增强,同时颗粒间孔隙变小,要使土中水排出就需要更大的基质吸力,这说明不同颗粒粒径含量对土-水特征曲线会产生较大的影响。
3 土-水特征曲线特征值及分维数D计算 3.1 土-水特征曲线特征值计算方法反映土-水特征曲线在非饱和土抗剪强度、渗透性和土体变形特性应用时,一般都会运用到土-水特征曲线的进气值、残余含水率和与之对应的残余基质吸力等这些特征量(见图 3),其中,进气值反映土体从饱和状态进入到非饱和状态时所对应的最小基质吸力值;残余基质吸力表示土体在非饱和状态下的最大基质吸力值。

|
图 3 土-水特征曲线中各点的定义 Figure 3 Definition of each point in soil-water characteristic curves |
以往在计算这些土-水特征曲线特征值时,通常采用作图法进行计算,但由于作图法得出的特征值往往会出现较大误差,这种误差在半对数坐标系图中会被放大,从而影响土-水特征曲线中特征值的准确性。Fredlund & Xing1模型最能拟合试验数据,适用性广,而且精度最高[19],所以采用Fredlund & Xing1模型对所得土-水特征曲线进行拟合,并在Qian Zhai等[20]计算特征值方法的基础上,计算土-水特征曲线的特征值。
Fredlund & Xing1模型表达式如式(2)
| $ \theta = \frac{{{\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {\psi /a} \right)}^b}} \right]} \right\}}^c}}} $ | (2) |
式中: ψ为基质吸力(kPa);θ为体积含水率;a,b,c均为模型参数;e为自然对数常量;θs为饱和体积含水率。
3.1.1 模型中第1个拐点的斜率土-水特征曲线中任意一点的斜率可以通过曲线方程一阶求导得出,即:
| $ s = \frac{{{\rm{d}}\theta }}{{{\rm{dlg}}\psi }} = \frac{{\partial \theta }}{{\partial \psi }}{\psi} \times \ln 10 = \frac{{\left( { - c} \right){\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {\psi /a} \right)}^b}} \right]} \right\}}^{c + 1}}}}\frac{b}{{e + {{\left( {\psi /a} \right)}^b}}}{\left( {\frac{\psi }{a}} \right)^b} \times \ln 10 $ | (3) |
因为曲线第1个拐点的吸力ψ=ψi=a,所以将ψ=a代入式(3)可以得到第1个拐点处的斜率s1,则有:
| $ {s_1} = {\left| {\frac{{{\rm{d}}\theta }}{{{\rm{dlg}}\psi }}} \right|_{\psi = a}} = \left| {\frac{{\left( { - c} \right){\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {a/a} \right)}^b}} \right]} \right\}}^{c + 1}}}}\frac{b}{{e + {{\left( {a/a} \right)}^b}}}{{\left( {\frac{a}{a}} \right)}^b} \times \ln 10} \right| = \frac{{c{\theta _{\rm{s}}}}}{{{{0.31}^{{\rm{c}} + 1}}}}{\frac{b}{{3.72}}} \times \ln 10 $ | (4) |
从图 3的几何关系可知,s1同时可以被定义为:
| $ {s_1} = \frac{{{\theta _{\rm{s}}} - {\theta _i}}}{{\lg \left( {{\psi _i}/{\psi _{\rm{b}}}} \right)}} = \frac{{{\theta _{\rm{s}}} - {\theta _i}}}{{\lg \left( {a/{\psi _{\rm{b}}}} \right)}} $ | (5) |
其中
| $ {\theta _i} = \frac{{{\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {a/a} \right)}^b}} \right]} \right\}}^c}}} = \frac{{{\theta _{\rm{s}}}}}{{{{1.313}^c}}} $ | (6) |
那么通过式(4)与式(5)即可得到模型中进气值的表达式如式(7):
| $ {\psi _{\rm{b}}} = a{0.1^{\frac{{3.72 \times {{1.31}^{c + 1}}\left( {1 - {e^{\frac{c}{{3.67}}}}} \right)}}{{bc \times \ln 10}}}} $ | (7) |
土-水特征曲线中在高基质吸力曲线开始线性下降时,可以把ψ′代入到式(3)中,得到点(ψ′,θ′)的斜率s2的表达式如下:
| $ {s_2} = \frac{{\left( { - c} \right){\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {\psi '/a} \right)}^b}} \right]} \right\}}^{c + 1}}}}\frac{b}{{e + {{\left( {\psi '/a} \right)}^b}}}{\left( {\frac{{\psi '}}{a}} \right)^b} \times \ln 10 $ | (8) |
该点的体积含水率可以通过将ψ′代入式(2)计算得出,即:
| $ \theta ' = \frac{{{\theta _{\rm{s}}}}}{{{{\left\{ {\ln \left[{e + {{\left( {\psi '/a} \right)}^b}} \right]} \right\}}^c}}} $ | (9) |
从图 3中曲线的几何关系可以得到:
| $ {s_1} = \frac{{{\theta _i} - {\theta _{\rm{r}}}}}{{\lg {\psi _{\rm{r}}} - \lg a}} $ | (10) |
| $ {s_2} = \frac{{{\theta _{\rm{r}}} - \theta '}}{{\lg \psi ' - lg{\psi _{\rm{r}}}}} $ | (11) |
然后将式(4)代入式(10),式(8)代入式(11),即可得到残余基质吸力,表达式如下:
| $ {\psi _{\rm{r}}} = {10^{\frac{{{\theta _i} - \theta ' + {s_1}\lg a - {s_2}\lg \psi '}}{{{s_1} - {s_2}}}}} $ | (12) |
按照上述计算式分别计算不同颗粒级配土样的土-水特征曲线特征值,表 1即为Fredlund & Xing1模型中拟合参数和特征值的计算结果。
| 表 1 各土样在Fredlund & Xing1模型中的拟合参数及特征值 Table 1 Fitting parameters and characteristic values of each soil sample in Fredlund & Xing1 model |
Turcotte[14]、杨培岭等[15]通过计算提出土体颗粒质量分布与粒径的分形关系
| $ \frac{{M\left( {\delta > {d_i}} \right)}}{{{M_{\rm{T}}}}} = 1 - {\left( {\frac{{{d_i}}}{{{d_{\max }}}}} \right)^{3 - D}} $ | (13) |
或
| $ {\left( {\frac{{{d_i}}}{{{d_{\max }}}}} \right)^{3 - D}} = \frac{{M\left( {\delta < {d_i}} \right)}}{{{M_{\rm{T}}}}} $ | (14) |
式中:MT表示土颗粒总质量; δ表示土颗粒粒径大小的尺码; M(δ < di)表示土颗粒粒径小于di的累积质量,简化为Mi表示; D表示分维数。
为了研究各颗粒级配下分维数D与土-水特征曲线特征值之间的关系,将式(14)变换即可得到式(15):
| $ 3 - D = \frac{{\lg \frac{{{M_i}}}{{{M_T}}}}}{{\lg \frac{{{d_i}}}{{{d_{\max }}}}}} $ | (15) |
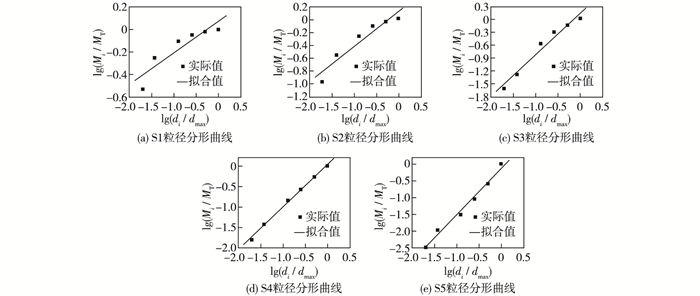
然后以lg(Mi/MT)和lg(di/dmax)分别为纵横坐标进行绘制,然后通过线性拟合可得到分维数D=3-k,其中k为直线斜率。各颗粒级配的粒径分形曲线结果如图 4。
|
图 4 各级配土样的粒径分形曲线 Figure 4 Grain size fractal curves of soil samples |
根据图 4可以看到不同颗粒级配土样均具有较好的分形特征,其拟合曲线复相关系数R2均在0.93以上,并且分维数D随着细粒土含量的减少而降低,这也与文献[12-13]的结论相吻合,即分维数D可以表征土样中细颗粒土的含量,分维数D越大表示土中细颗粒土含量越高,粗颗粒土含量越少;反之则土中细颗粒土含量越少,粗颗粒土含量越高。
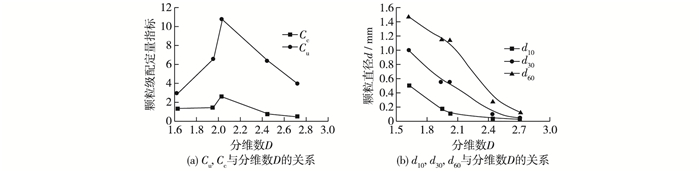
4 分维数D与各指标的关系 4.1 分维数D与级配定量指标及关键粒径间关系为了分析不同颗粒级配土样与分数D之间的关系,绘制不均匀系数Cu和曲率系数Cc及关键粒径与分维数D的关系图(如图 5)。Cu表示粒度分布范围,Cu越大表明土粒越不均匀,级配越好;Cc描述累积曲线分布整体形态,而分维数D则描述粒组中细颗粒的含量。由图 5(a)可以看出不均匀系数Cu和曲率系数Cc均随分维数D的增加呈先增后减的规律,这是因为S3粒组在这5组土样中为最优级配粒组,Cu, Cc指标均表示其级配良好;而其余4组土样的级配是通过人工配制的,级配比S3粒组较差,这也反映出分维数D并不是越大就代表级配越好,而是细颗粒在土中含量适中才能有良好级配,也就是分维数D在一定范围内可以表达土样级配的良好性。这也与文献[21]的部分结论相一致。
|
图 5 级配定量指标及关键粒径与分维数D的关系 Figure 5 Relationship curves between Cu, Cc, critical grain size and fractal dimension D |
图 5(b)描述了分维数D与各关键粒径间的关系,从图中可以看到不论是d10,d30还是d60均随着分维数D增大而减小。在粒径累积曲线中关键粒径逐渐减小表征粒组的整体粒径变小,粒组中细颗粒含量增多。因此根据此图的变化曲线也可以得出分维数D可描述细颗粒的含量,细颗粒含量越多分维数D越大的结论。
4.2 分维数D与土-水特征曲线特征值的关系土样粒组中各粒径的含量在很大程度上影响着土-水特征曲线,通过分形理论中分维数D指标描述粒组中细颗粒的含量,然后将分维数D与土-水特征曲线特征值建立联系,分析得出各颗粒含量对土-水特征曲线的影响。
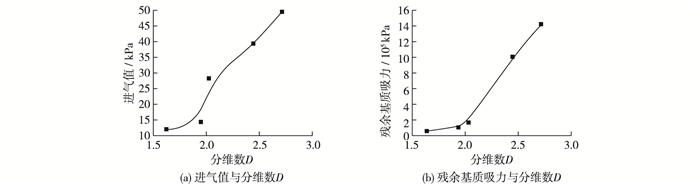
图 6为分维数D与土-水特征曲线特征值之间的关系。可见,进气值随着分维数D的增大而提高,通过线性拟合可以得到其复相关系数R2=0.97,所以可认为是线性增长。这是因为土体中细颗粒含量越高,则土颗粒的单位比表面积越大,其吸附能力也就越强;同时土颗粒越细,在相同干密度条件下会具有更高的密实度,所组成土体中孔隙就越小,这样就使得细颗粒含量高的土样进气值高,不易排水,即分维数D越大,进气值越大。
|
图 6 土-水特征曲线特征值与分维数D的关系 Figure 6 Relationships between characteristic values of soil-water characteristic curves and fractal dimension D |
残余基质吸力也随着分维数D的增大而提高,但在分维数D较小时,残余基质吸力的增长幅度很小,分维数D较大时残余基质吸力的增幅会大幅增大。粗颗粒含量越高的土,土体中粒间孔隙会越大,水气交界薄膜曲率半径会增大,使得土体在非饱和状态下具有的最大基质吸力值会变小,所以残余基质吸力就会随着分维数D的减小而减小。由于毛细作用在粗颗粒土中不如在细颗粒土中活跃,所以细颗粒土对含水率变化的敏感性好于粗颗粒土,因此在分维数D较小时残余基质吸力值低并且增幅较小。
5 结语(1) 所研究的江西红土均具有较好的分形特征,并且分维数D随着细粒土含量的减少而降低,随着粗颗粒含量的增多而增大。
(2) 颗粒级配定量指标Cu,Cc均随分维数D的增加先增后减,粒径累积曲线中关键粒径d10,d30及d60均随分维数D增大而减小。
(3) 通过将分维数D与土-水特征曲线特征值建立联系分析得到,土-水特征曲线中进气值随着分维数D的增大而提高,线性拟合后其复相关系数为0.97,可认为线性增长;同时残余基质吸力值也随分维数D的增大而变大。
本文以同一种土质的不同颗粒粒径含量作为研究对象,后续将采用多类型土作为研究对象,针对分维数D与土-水特征曲线特征值的关系进行更为深入地研究。
| [1] |
刘小文, 叶云雪. 不同影响因素下非饱和红土土-水特征曲线的试验研究[J]. 水文地质工程地质, 2015, 42(2): 97-104. ( LIU Xiaowen, YE Yunyue. Experimental study of the soil-water characteristic curve of unsaturated laterite under different affecting factors[J]. Hydrogeology & Engineering Geology, 2015, 42(2): 97-104. (in Chinese)) |
| [2] |
LU Ning, LIKOS W J.非饱和土力学[M].韦昌富, 侯龙, 简文星, 译.北京: 高等教育出版社, 2012. (LU Ning, LIKOS W J. Unsaturated soil mechanics[M]. Translated by WEI Changfu, HOU Long, JIAN Wenxing. Beijing: High Education Press, 2012. (in Chinese))
|
| [3] |
弗雷德隆德D G, 拉哈尔佐H.非饱和土土力学[M].陈仲颐, 张在明, 陈愈炯, 等, 译.北京: 中国建筑工业出版社, 1997. (FREDLUND D G, RAHARDJO H. Soil mechanical for unsaturated soils[M]. Translated by CHEN Zhongyi, ZHANG Zaiming, CHEN Yujiong, et al. Beijing: China Building Industry Press, 1997. (in Chinese))
|
| [4] |
陈东霞, 龚晓南. 非饱和残积土的土-水特征曲线试验及模拟[J]. 岩土力学, 2014, 35(7): 1885-1891. ( CHEN Dongxia, GONG Xiaonan. Experiment and modeling of soil-water characteristic curve of unsaturated residual soil[J]. Rock and Soil Mechanics, 2014, 35(7): 1885-1891. (in Chinese)) |
| [5] |
文宝萍, 胡艳青. 颗粒级配对非饱和粘性土基质吸力的影响规律[J]. 水文地质工程地质, 2008, 26(6): 50-55. ( WEN Baoping, HU Yanqing. Effect of particle size distribution on the metric suction of unsaturated clayey soils[J]. Hydrogeology & Engineering Geology, 2008, 26(6): 50-55. DOI:10.3969/j.issn.1000-3665.2008.06.012 (in Chinese)) |
| [6] |
李志清, 胡瑞林, 王立朝, 等. 非饱和膨胀土SWCC研究[J]. 岩土力学, 2006, 27(5): 730-734. ( LI Zhiqing, HU Ruilin, WANG Lichao, et al. Study on SWCC of unsaturated expansive soil[J]. Rock and Soil Mechanics, 2006, 27(5): 730-734. DOI:10.3969/j.issn.1000-7598.2006.05.009 (in Chinese)) |
| [7] |
赵天宇, 王锦芳. 考虑密度与干湿循环影响的黄土SWCC[J]. 中南大学学报(自然科学版), 2012, 43(6): 2446-2453. ( ZHAO Tianyu, WANG Jinfang. Soil-water characteristic curve for unsaturated loess soil considering density and wetting-drying cycle effects[J]. Journal of Central South University (Science and Technology), 2012, 43(6): 2446-2453. (in Chinese)) |
| [8] |
王铁行, 岳彩坤, 卢靖. 考虑温度和密度影响的非饱和黄土-土水特征曲线研究[J]. 岩土力学, 2008, 29(1): 1-5. ( WANG Tiexing, YUE Caikun, LU Jing. Soil-water characteristic curve for unsaturated loess considering temperature and density effect[J]. Rock and Soil Mechanics, 2008, 29(1): 1-5. DOI:10.3969/j.issn.1000-7598.2008.01.001 (in Chinese)) |
| [9] |
王铁行, 王晓峰. 密度对砂土基质吸力的影响研究[J]. 岩土力学, 2003, 24(6): 979-982. ( WANG Tiexing, WANG Xiaofeng. Influence of density on matrix suction of sandy soil[J]. Rock and Soil Mechanics, 2003, 24(6): 979-982. DOI:10.3969/j.issn.1000-7598.2003.06.023 (in Chinese)) |
| [10] |
李龙起, 书学, 姜红, 等. 非饱和红黏土-土水特性及强度特征研究[J]. 西南交通大学学报, 2014, 49(3): 393-431. ( LI Longqi, SHU Xue, JIANG Hong, et al. Soil-Water and shear strength characteristics of unsaturated red clay[J]. Journal of Southwest Jiaotong University, 2014, 49(3): 393-431. DOI:10.3969/j.issn.0258-2724.2014.03.004 (in Chinese)) |
| [11] |
朱赞成, 孙德安, 田进. 高吸力高温度下2种滤纸率定曲线及其应用[J]. 岩土工程学报, 2014, 36(6): 1020-1027. ( ZHU Zancheng, SUN Dean, TIAN Jin. Calibration curves of two filter papers at high suction and temperature and their application[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1020-1027. (in Chinese)) |
| [12] |
陶高梁, 张季如, 庄心善, 等. 描述黏粒含量对土-水特征曲线影响规律的分形模型[J]. 水利学报, 2014, 45(4): 490-496. ( TAO Gaoliang, ZHANG Jiru, ZHUANG Xinshan, et al. A fractal model describing the relation between clay content and soil-water characteristic curve[J]. Journal of Hydraulic Engineering, 2014, 45(4): 490-496. (in Chinese)) |
| [13] |
张季如, 胡泳, 于红玲, 等. 黏性土粒径分布的多重分形特性及土-水特征曲线的预测研究[J]. 水利学报, 2015, 46(6): 650-657. ( ZHANG Jiru, HU Yong, YU Hongling, et al. Predicting soil-water characteristic curve from multi-fractal particle-size distribution of clay[J]. Journal of Hydraulic Engineering, 2015, 46(6): 650-657. (in Chinese)) |
| [14] |
TURCOTTE D L. Fractals andfragmentation[J]. Journal of Geophysical Research, 1986, 91(B2): 1921-1926. |
| [15] |
TYLER S W, WHEATCRAFT S W. Fractal scaling of soil particle-size distributions: analysis and limitations[J]. Soil Science Society of America Journal, 1992, 56(2): 362-369. DOI:10.2136/sssaj1992.03615995005600020005x |
| [16] |
白福青, 刘斯宏, 袁娇. 滤纸总吸力吸湿曲线的率定试验[J]. 岩土力学, 2011, 32(8): 2336-2340. ( BAI Fuqing, LIU Sihong, YUAN Jiao. Measurement of SWCC of Nanyang expansive soil using the filter paper method[J]. Chinese Journal of Geotechnical Engineering, 2011, 32(8): 2336-2340. DOI:10.3969/j.issn.1000-7598.2011.08.015 (in Chinese)) |
| [17] |
唐栋, 李典庆, 金浩飞, 等. 国产"双圈"牌滤纸吸力率定曲线研究[J]. 武汉大学学报(工学版), 2016, 49(1): 1-8. ( TANG Dong, LI Dianqing, JIN Haofei, et al. Research on calibration curves of home-made "Double Circle" filter papers[J]. Engineering Journal of Wuhan University, 2016, 49(1): 1-8. (in Chinese)) |
| [18] |
况娟娟.非饱和土滤纸法吸力量测及影响规律的研究[D].武汉: 武汉水利电力大学, 1998. (KUANG Juanjuan. Study on suction measurement and influence law of unsaturated soil filter paper[D]. Wuhan: Wuhan University of Hydraulic and Electric Engineering, 1998. (in Chinese))
|
| [19] |
陈宇龙, 内村太郎. 粒径对土持水性能的影响[J]. 岩石力学与工程学报, 2016, 35(7): 1474-1482. ( CHEN Yulong, UCHIMURA Taro. Influence of particle size on water retention of soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(7): 1474-1482. (in Chinese)) |
| [20] |
QIAN Z, HARIANTO R. Determination of soil-watercharacteristic[J]. Computers and Geotechnics, 2012, 42: 37-43. DOI:10.1016/j.compgeo.2011.11.010 |
| [21] |
王育刚.基于分形理论的土体物理力学性能试验研究[D].长沙: 长沙理工大学, 2011. (WANG Yugang. Experimental study on physical and mechanical properties of soil based on fractal theory[D]. Changsha: Changsha University of Science and Technology, 2011. (in Chinese))
|
 2018
2018 

