2. 南京市水利规划设计院股份有限公司, 江苏 南京 210006
长江河口是我国最大的河口, 上起徐六泾, 在平面上呈三级分汊、四口入海的河势格局。崇明岛将长江口分为北支和南支, 长兴岛和横沙岛将南支分为北港和南港, 九段沙将南港分为北槽和南槽(图 1)。长江口水量丰沛, 水体自净能力强, 为沿岸居民提供了丰富的淡水资源。从1883年开始, 上海市取水口位于黄浦江。由于黄浦江处于太湖流域下游, 随着时间推移, 上游污染影响下水质较差且不稳定性的问题日益凸显。因此, 有必要寻找新水源地。从20世纪90年代开始, 长江口三大水源地——陈行水库、青草沙水库和东风西沙水库相继建成(图 1), 目前供水规模已达上海市的80%左右。因此长江口水源地安全对上海市经济发展和人民生活产生重要影响。

|
图 1 长江口水源地位置 Figure 1 Positions of water sources in Yangtze River estuary |
由于三大水源地取水口均位于河口地区, 枯季盐水入侵成为水源地安全最主要的威胁。根据《地表水环境质量标准》(GB 3838—2002)及相关规范要求, 盐度超过0.45‰时不可作为饮用水。径流和潮汐是影响河口盐水入侵的主要因素, 20世纪80年代初的研究即已经涉及径流和潮汐对盐度分布的影响[1]。安徽大通水文站距离长江口600多千米, 是距离长江口最近且不受潮汐影响的水文站, 因此大通的径流量可表示长江口径流特征[2]。罗小峰等[3]通过不同径潮组合的数值模拟表明, 径流直接影响盐水入侵距离、潮汐影响盐水回荡范围。侯成程等[4]研究了长江口盐水入侵对大通枯季径流量变化的响应时间。Qiu等[5]研究了涨落潮、大小潮以及潮汐季节变化对长江口盐水入侵影响。长江口三级分汊四口入海的河势格局又使得盐水入侵的时空分布更为复杂[6], Qiu等[5]认为不同的潮汐强度会使各汊道分流比发生改变, 进一步影响盐度的空间分布。北支的盐水倒灌是长江口盐水入侵的一个重要特征。因北支分流比低于5%而进潮量占整个长江口的25%左右, 因此北支是长江口盐水入侵最严重的汊道。北支高浓度盐水在径流较小、潮动力较强时会倒灌进入南支。丁磊等[7]对2013, 2014年南北支分汊口处盐度实测资料进行分析, 研究了北支盐水倒灌的影响因素及下泄路径。Wu等[8]研究了径潮动力对北支倒灌盐通量的影响。陈敏建等[9]研究了南支盐度超标面积与径流、潮差的函数关系。孙昭华等[10]将潮差关系与农历日期建立联系, 提出了一种仅需知道大通流量就可快速估算北支盐水倒灌影响下南支特定水域盐度的方法。
东风西沙水库和陈行水库取水口位于南支水域, 青草沙水库取水口位于北港水域, 均会不同程度受到北支盐水倒灌的影响。关于北支盐水倒灌物理过程的表征, 以往是通过基于盐度场的等值线图或是纵剖面盐度图进行表示[11], 该方法能够从场的角度形象体现盐水倒灌的平面过程, 但无法刻画盐度随时间的连续变化。而实际上测点盐度过程线和潮位过程线的关系也可反映盐水来源, 此前鲜有这方面的详细分析。同时, 倒灌盐水团对三大水源地影响时间的研究也较少。因此, 本文通过建立数学模型对长江口水-盐动力特性进行模拟, 对不同径潮动力下长江口水源地受盐水入侵的影响展开研究。研究结果可作为长江口淡水资源利用及水源地安全研究的依据, 为其他河口水源地建设和运行调度提供参考。
1 长江口水文情势长江口地区水资源总量为42.33亿m3, 其中地表水资源量38.00亿m3。长江入海水量年内分配不均匀, 基本表现为洪季(5—10月)流量大, 枯季(11月至次年4月)流量小。
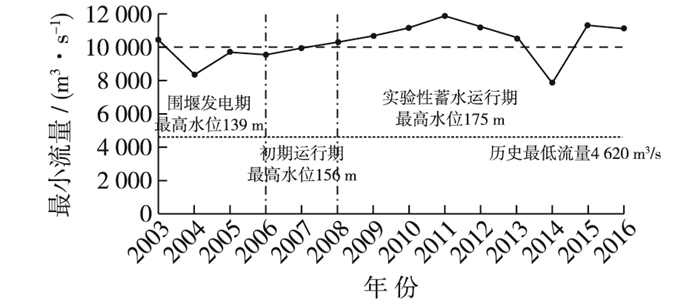
根据大通站1950—2016年资料统计, 大通站多年平均流量28 300 m3/s, 1954年8月1日出现最大流量92 600 m3/s, 1979年1月31日出现最小流量为4 620 m3/s。三峡工程使得长江流量的年内分布发生改变, 枯季流量总体增加。2003年三峡水库蓄水后各年最小流量如图 2所示。最小流量不会低于5 000 m3/s, 尤其是到试验性蓄水运行期(2008年汛后开始)时, 仅2014年出现低于10 000 m3/s的流量。
|
图 2 大通水文站年最小流量 Figure 2 Annual minimum runoff of Datong station |
长江口为中等潮差河口, 中竣站年平均潮差2.66 m, 最大潮差4.62 m。河口口门处总进潮量为13亿m3(枯季小潮)~53亿m3(洪季大潮)。潮汐受外海潮波控制, 口外潮汐为正规半日潮, 口内潮汐为非正规浅海半日潮。东海前进波系统在本区域M2分潮为主, 起支配作用; 其次还受到黄海旋转潮波影响, 以K1和O1分潮较显著。潮波进入长江口区域后, 受边界条件和上游径流影响, 潮波发生变形, 既非典型的前进波, 也非典型的驻波。
2 模型的建立与验证目前能搜集到的长江口高精度盐度资料主要来源于同步全潮水文测验, 优点是精度高且为多点同步测量, 缺点是成本高因而缺乏连续性。因此建立数学模型并用实测资料进行验证是较为常用的研究手段。长江口枯季大部分区域盐淡水混合类型为缓混合型, 北支为强混合型, 盐度垂线差异较小, 盐水楔不明显, 因此采用平面二维数学模型可以对长江口的盐水入侵进行较好模拟, 国内学者有较为成功的经验[3, 12]。但因长江口人类活动明显, 局部地形变化较快, 盐水入侵会因此受到影响, 采取不同地形会使研究结果产生差异。因此建立采用较新实测地形的数学模型和利用最近的实测资料对模型进行验证较为必要。
2.1 模型介绍利用Delft3D软件建立长江口大范围平面二维潮流盐度数学模型对盐度输运进行模拟。De1ft3D是由荷兰Delft水力研究院开发的, 是目前较为先进的水动力、水质、泥沙等模型系统之一。Delft3D由6个模块组成, 各模块既独立又相互联系, 能较精确地进行大尺度水流(Flow)、水动力(Hydro-dynamics)、波浪(Waves)、泥沙(Morphology)、水质(Waq)和生态(Eco)计算。Delft3D模型的计算稳定性强, 采用干湿动边界处理技术, 对河口海岸区域有较好适应性, 可快速解决网格绘制、水深参数插值等问题, 并具有强大的后处理功能。主要利用其中的Flow模块对长江口盐度输运过程进行模拟研究。
水动力计算的浅水方程基于Navier-Stokes方程。控制方程如下:
连续性方程:
| $ \frac{{\partial \zeta }}{{\partial t}} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\left\{ {\frac{{\partial \left[{\sqrt {{G_{\eta \eta }}} \left( {d + \zeta } \right)u} \right]}}{{\partial \xi }} + \frac{{\partial \left[{\sqrt {{G_{\xi \xi }}} \left( {d + \zeta } \right)v} \right]}}{{\partial \eta }}} \right\} = Q $ | (1) |
| $ Q = H\int\limits_{-1}^0 {\left( {{q_{{\text{in}}}}-{q_{{\text{out}}}}} \right){\text{d}}\sigma + P-E} $ | (2) |
式中:ζ为参考基面上自由表面高程, d为参考基面下的水深(m);
水平动量方程为:
| $ \frac{{\partial u}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial u}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial u}}{{\partial \eta }} + \\ \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }}-\frac{{{v^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \xi }}-fv =-\frac{{{P_\xi }}}{{{\rho _0}\sqrt {{G_{\xi \xi }}} }} + {F_\xi } + {M_\xi } $ | (3) |
| $ \frac{{\partial v}}{{\partial t}} + \frac{u}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial v}}{{\partial \xi }} + \frac{v}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial v}}{{\partial \eta }} + \\ \frac{{uv}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\xi \xi }}} }}{{\partial \eta }}-\frac{{{u^2}}}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\frac{{\partial \sqrt {{G_{\eta \eta }}} }}{{\partial \eta }} + fu =-\frac{{{P_\eta }}}{{{\rho _0}\sqrt {{G_{\eta \eta }}} }} + {F_\eta } + {M_\eta } $ | (4) |
式中:f为科里奥利参数(1/s); ρ0为水体密度(kg/m3); Pξ, Pη为ξ, η方向的静水压力梯度(kg/(m2·s2)); Fξ, Fη为ξ, η方向的紊动动量通量(m/s2); Mξ, Mη为ξ, η方向的动量源或汇(m/s2)。
在Delft 3D-FLOW模块中, 物质输运采用对流扩散方程进行模拟。输运方程以守恒形式呈现:
| $ \begin{gathered} \frac{{\partial \left( {d + \zeta } \right)c}}{{\partial t}} + \frac{1}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\left\{ {\frac{{\partial \left[{\sqrt {{G_{\eta \eta }}} \left( {d + \zeta } \right)uc} \right]}}{{\partial \xi }} + \frac{{\partial \left[{\sqrt {{G_{\xi \xi }}} \left( {d + \zeta } \right)vc} \right]}}{{\partial \eta }}} \right\} \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;=\frac{{d + \zeta }}{{\sqrt {{G_{\xi \xi }}} \sqrt {{G_{\eta \eta }}} }}\left\{ {\frac{\partial }{{\partial \xi }}\left( {{D_{\text{H}}}\frac{{\sqrt {{G_{\eta \eta }}} }}{{\sqrt {{G_{\xi \xi }}} }}\frac{{\partial c}}{{\partial \xi }}} \right) + \frac{\partial }{{\partial \eta }}\left( {{D_{\text{H}}}\frac{{\sqrt {{G_{\xi \xi }}} }}{{\sqrt {{G_{\eta \eta }}} }}\frac{{\partial c}}{{\partial \eta }}} \right)} \right\} \hfill \\ \end{gathered} $ | (5) |
式中:c为盐度; DH为水平扩散系数(m/s2)。
模型采用正交曲线网格, 且可以使网格线最大程度地贴合边界线, 避免“阶梯”边界导致发散。模型基于有限差分数值方法。时间项的离散采用ADI差分格式, 将1个时间步长分成2步, 每一步为半个时间步长, 前、后半个步长分别对不同方向进行隐式处理。
2.2 模型建立计算范围及网格如图 3所示, 包括长江口、杭州湾及邻近海域。北边界位于北纬34.67°, 南边界最远位于北纬29.33°, 东边界最远位于东经124.24°, 东、南、北开边界采用水位边界, 由主要分潮调和分析所得。上游边界取在大通, 为流量控制, 验证时使用大通站逐时实测流量。横向网格1 431个, 纵向163个。外海处网格尺寸最大达到2 km×2 km, 长江口区域进行了局部加密处理, 最小网格尺寸为70 m×60 m。

|
图 3 模型整体和局部网格 Figure 3 Entire and local model grids |
江阴以下至长江口地形为2011年实测地形, 江阴至大通为2006年实测地形。外海由海图数字化得到。坐标为高斯-克吕克坐标, 高程统一为85高程系统。根据柯朗数(Courant number)原则, 时间步长取15 s。模型糙率由谢才系数提供, 根据地形情况采用不同的数值, 范围为80~200 m1/2/s。模型初始流速和初始水位设为0。外海边界盐度为35‰, 长江口内根据实测资料进行插值, 大通边界盐度为0, 大通至徐六泾的盐度由线性插值得到。扩散系数为250 m2/s。模型计算运行4个月(8个完整的半月周期)作为初始场进行验证。
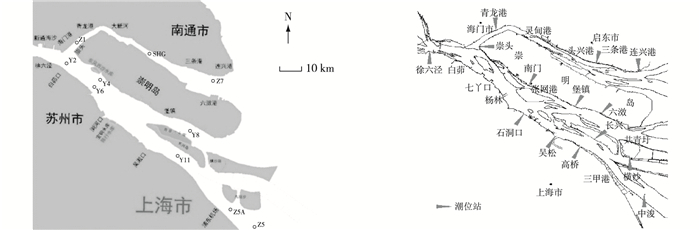
2.3 模型验证模型采用2016年1月长江口大范围全潮同步水文测验进行水动力与盐度的验证。本次测验共布置10条垂线, 基本覆盖了长江口水域, 同时还搜集了测验期间连兴港、青龙港、崇头、徐六泾、白茆、六滧(南)、高桥等潮位(图 4)。
|
图 4 水文测验测点及潮位站 Figure 4 Hydrological test vertical lines and tidal stations |
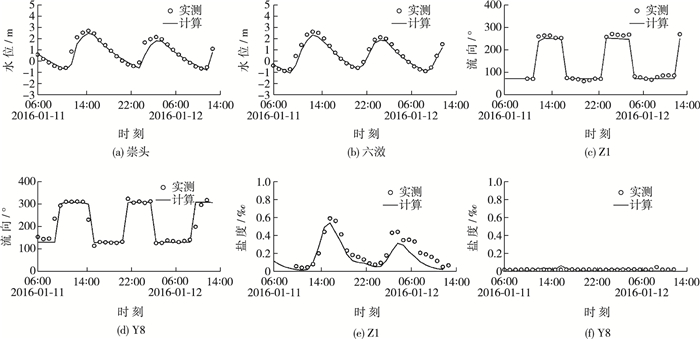
对大、中、小潮水位、流速、流向及盐度进行了验证。鉴于篇幅关系仅给出大潮时崇头、六滧潮位验证及Z1, Y8流速、流向和盐度验证结果(图 5)。可以看出, 该模型能较好地模拟长江口水动力及盐度输运。
|
图 5 模型验证结果 Figure 5 Results of model verification |
数学模型计算时, 上游采用恒定流。潮汐方面, 取验证时的完整半月周期闭合循环计算。模型计算运行4个月(8个完整的半月周期)作为初始场。分析时间为16 d, 包含1个完整的半月周期, 从最大潮差出现前4 d开始, 再到最小潮差出现后4 d结束。
3.2 水源地取水口盐度过程长江口水源地取水口盐度会随涨落潮变化, 若落潮时盐度上升, 涨潮时盐度下降, 该现象表明该处盐水来源于取水口上游, 即受北支倒灌盐水影响; 若涨潮时盐度上升, 落潮时盐度下降, 则表明该处盐水来源于取水口下游, 为外海盐水正面影响或已经下泄到取水口下游的盐水团随涨潮流上溯所致。不同径流下, 水源地取水口盐度大小不同, 但盐度过程变化特征较为相似。以大通径流为12 500 m3/s(接近1月径流50%频率)为例[13-14], 分析3个水源地取水口盐度过程特征。对不同水源地而言, 因受北支倒灌盐水和正面入侵盐水程度不同, 盐度过程也有着不同的特征。
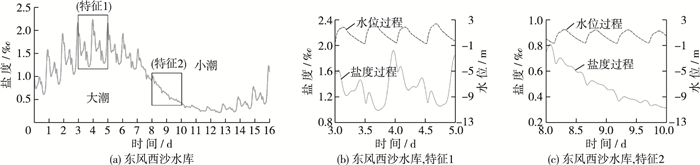
3.2.1 东风西沙水库东风西沙水库取水口在半月周期中, 盐度过程与水位过程的关系根据潮差大小, 表现出两种不同的特征(图 6(a))。潮差较大时, 盐度过程1 d内出现4个极大值。涨潮时盐度上升, 落潮时盐度短暂下降后再次上升, 且落潮时出现的盐度极大值比涨潮时大得多(图 6(b))。随着潮差减小, 盐度过程整体呈下降趋势。潮差小到一定程度时, 落潮时的盐度极大值消失, 除了涨潮时盐度有较小的上升外, 盐度总体呈下降趋势(图 6(c)), 即该阶段北支不再出现盐水倒灌。最小潮出现以后, 落潮时盐度极大值又逐渐出现, 表现为图 6(b)所示特征。对日平均盐度进行计算, 发现半月周期中日均盐度最大值出现在大潮当天, 较高盐度持续到大潮后的中潮, 日均盐度上升时间略高于下降时间。
|
图 6 东风西沙水库取水口盐度过程与水位过程 Figure 6 Salinity and water level hydrograph in Dongfengxisha reservoir intake |
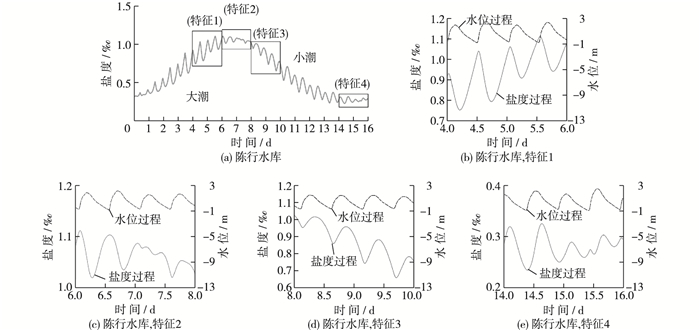
陈行水库取水口盐度过程没有出现单一的周期振动规律。在半月周期中, 盐度过程与水位过程的关系表现出了4种不同的特征(图 7(a))。大潮前的中潮后期及大潮期, 盐度在1 d内表现为两涨两落, 涨潮时盐度降低, 落潮时盐度升高。盐度总体呈上升趋势, 且逐渐变缓(图 7(b))。此后, 有半天盐度特征发生改变, 落潮时盐度上升后, 涨潮时并没有立即下降, 该阶段盐度变化较小且稳定在一个较高的值, 直到落潮的后期(落急以后)盐度又明显下降(图 7(c))。此后盐度又恢复1 d内两涨两落, 但仍然表现为涨潮时盐度上升落潮时下降, 盐度总体呈下降趋势(图 7(d))。该特征一直持续到小潮后的中潮, 盐度总体下降到一定程度后不再下降, 且出现新的特征。落潮时再次出现盐度升高, 且越来越明显, 1 d内出现4个盐度峰值(图 7(e))。日均盐度最大值出现在大潮后的中潮, 较高盐度持续到小潮, 且从最小值上升到最大值持续时间与最大值下降到最小值基本相同。
|
图 7 陈行水库取水口盐度过程与水位过程 Figure 7 Salinity and water level hydrograph in Chenhang reservoir intake |
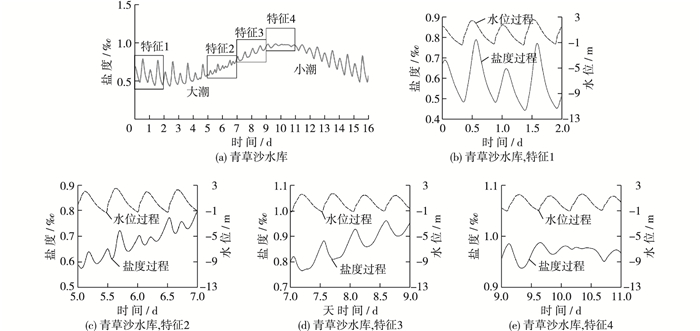
青草沙水库取水口盐度过程表现出4种不同特征(图 8)。如图 8(a)所示, 小潮后期至大潮后期, 涨潮时盐度上升, 落潮时盐度下降, 日盐度变化幅度在四种特征中最大。大潮后期及大潮后的中潮盐度日变化不再为两涨两落, 1 d内出现4个盐度峰值, 除涨潮时盐度上升外, 落潮时盐度在短暂下降后也会有上升。盐度总体趋势为波动中上升(图 8(b)), 振幅相对前一阶段减小。这种现象持续2 d后再次发生改变, 盐度过程再次表现为1 d内两涨两落, 但与第一阶段不同的是, 涨潮时盐度下降而落潮时盐度上升。涨潮时的盐度峰值消失而第二阶段中出现的落潮峰值继续出现。盐度总体趋势仍为波动中上升(图 8(c))。该阶段持续3 d左右又发生改变, 涨潮时盐度不再下降, 而是保持在一个相对固定的值, 该现象持续1 d左右, 在落潮时盐度再次下降(图 8(d)), 此时为小潮, 盐度过程再次表现为第一阶段的特征。日均盐度最大值出现在小潮, 较高盐度持续到小潮后的中潮, 表现出了明显的盐度下降时间长于上升时间。
|
图 8 青草沙水库取水口盐度过程与水位过程 Figure 8 Salinity and water level hydrograph in Qingcaosha reservoir intake |
大通流量高于20 000 m3/s时几乎不会有盐水倒灌现象。模型上游流量取8 000~20 000 m3/s时, 每500 m3/s设置1个工况进行计算。表 1给出了不同大通流量条件下, 半月周期中崇头、东风西沙水库、陈行水库以及青草沙水库最大日平均盐度出现时间。受正面入侵盐水影响时, 表现为大潮盐水入侵强, 小潮盐水入侵弱。若南支以下水域半月周期中盐度最大值出现在大潮后的其他时段, 则为北支盐水倒灌的影响[6]。水源地取水口日平均盐度最大值出现时间与崇头日平均盐度最大值出现时间的差值可以表示北支倒灌最高浓度盐水团运动到水源地取水口所需要的时间。
| 表 1 日平均盐度最大值出现时间 Table 1 Occurrence time for maximum value of daily average salinity |
流量小于14 500 m3/s时, 崇头日平均盐度最大出现在分析的第5 d, 即最大潮差出现当天。流量大于14 500 m3/s时, 崇头最大盐度出现在分析的第6 d, 即最大潮出现的后1天。虽然北支分流比小, 但随着流量增大会使得进入北支的径流量增大, 对盐水上溯起到了顶托作用, 使得最大盐度出现时间延迟。
东风西沙水库附近水域盐水来源主要为北支的倒灌, 最大盐度出现时间均比崇头滞后1 d。说明倒灌盐水团从崇头运动到东风西沙水库取水口需要1 d时间, 取水口在大潮时受北支倒灌盐水团影响最严重。
陈行水库日平均盐度最大值出现时间比东风西沙水库滞后, 但随着流量增大, 滞后时间逐渐变短。流量Q < 10 000 m3/s时滞后3 d; 10 000 m3/s≤Q < 14 500 m3/s时滞后2 d; Q≥14 500 m3/s时滞后1 d。倒灌盐水团从崇头运动到陈行水库取水口需要2~4 d, 取水口在大潮后的中潮时受北支倒灌盐水团影响最为严重。
青草沙水库日平均盐度最大值出现时间比东风西沙水库滞后, 且长于陈行水库的滞后时间。随着流量的增大, 滞后时间也逐渐变短, 对径流的响应比陈行水库更为敏感。当大通流量Q < 8 500 m3/s时, 青草沙水库取水口最大盐度出现时间比东风西沙水库取水口滞后8 d; 8 500 m3/s≤Q < 10 000 m3/s时滞后7 d; 10 000 m3/s≤Q < 12 000 m3/s时滞后6 d; 12 000 m3/s≤Q < 14 500 m3/s时滞后5 d; Q≥14 500 m3/s时滞后4 d。倒灌盐水团从崇头运动到青草沙水库取水口需要5~9 d, 取水口在小潮时受北支倒灌盐水团影响最为严重。
径流量的增大使得北支倒灌水体进入南支后下泄速度加快, 因此陈行水库与青草沙水库附近水域均表现出随大通流量的增大, 受倒灌盐水团影响时间提前的特点。图 9为水源地取水口在半月周期中日均盐度的最大值与流量的关系。如图所示, 径流越大, 盐水入侵程度越弱, 受倒灌盐水团影响的程度也越弱。以往的研究指出流量与盐度呈指数关系, 而本文进一步研究时发现, 当流量在一定范围内时, 盐度与径流表现出很好的线性关系:

|
图 9 水源地取水口盐度与流量关系 Figure 9 Relationship curves between salinity and discharge of water intakes at water sources |
东风西沙水库:y=-0.000 4x+7.5(8 000≤x≤18 000)
陈行水库:y=-0.000 4x+6.0(8 000≤x≤14 000)
青草沙水库:y=-0.000 3x+4.9(8 000≤x≤16 000)
5 结语基于Delft3D建立长江口平面二维潮流盐度数学模型。利用2016年长江口大范围同步全潮水文测验资料对测验期间大、中、小潮的流速、流向、水位、盐度进行验证。验证效果良好, 可以对长江口的水-盐动力特性进行模拟, 对径潮动力影响下长江口水源地取水口盐度进行研究, 得出如下结论:
长江口枯季盐水入侵会威胁水源地安全。北支盐水倒灌是南支、北港水源地安全威胁的重要来源。三大水源地因位置不同, 盐度过程线特征也不相同。若落潮时盐度上升, 涨潮时盐度下降, 表明该处盐水来源于取水口上游, 即受北支倒灌盐水影响; 若涨潮时盐度上升, 落潮时盐度下降, 则表明该处盐水来源于取水口下游, 为外海盐水正面影响或已经下泄到取水口下游的盐水团随涨潮流上溯所致。水源地取水口盐度过程线与潮位过程线的关系可作为受北支倒灌盐水和正面入侵盐水影响程度的重要依据。
从南北支分汊口处崇头开始计算, 北支倒灌盐水团影响到东风西沙水库、陈行水库、青草沙水库取水口分别需要1, 2~4和5~9 d。水源地分别在大潮、大潮后的中潮以及小潮时受倒灌盐水影响最为严重。随着径流增大, 水源地受盐水入侵影响的时间会提前, 但是盐度随径流增大而直线下降。
| [1] |
韩乃斌. 长江口南支河段氯度变化分析[J]. 水利水运科学研究, 1983(1): 74-81. ( HAN Naibin. Analysis of chlorinity change in South Branch of Yangtze Estuary[J]. Journal of Nanjing Hydraulic Research Institute, 1983(1): 74-81. (in Chinese)) |
| [2] |
丁磊, 窦希萍, 高祥宇, 等.北支建闸对长江口水源地盐水入侵影响研究[C]//中国海洋学会海洋工程分会.第十八届中国海洋(岸)工程学术讨论会论文集(下), 2017. (DING Lei, DOU Xiping, GAO Xiangyu, et al. The influence of construction of tidal gate in the North Branch on water sources salinity intrusion in the Yangtze Estuary[C]// China Ocean Engineering Academy. The 18th China Ocean and Coast Engineering Symposium(volume two), 2017. (in Chinese))
|
| [3] |
罗小峰, 陈志昌. 长江口水流盐度数值模拟[J]. 水利水运工程学报, 2004(2): 29-33. ( LUO Xiaofeng, CHEN Zhichang. Numerical simulation of salinity in Yangtze River Estuary[J]. Hydro-Science and Engineering, 2004(2): 29-33. DOI:10.3969/j.issn.1009-640X.2004.02.005 (in Chinese)) |
| [4] |
侯成程, 朱建荣. 长江河口盐水入侵对大通枯季径流量变化的响应时间[J]. 海洋学报(中文版), 2013, 35(4): 29-35. ( HOU Chengcheng, ZHU Jianrong. The response time of saltwater intrusion in the Changjiang River Estuary to the change of river discharge in dry season[J]. Acta Oceanologica Sinica(in Chinese), 2013, 35(4): 29-35. DOI:10.3969/j.issn.0253-4193.2013.04.004 (in Chinese)) |
| [5] |
QIU C, ZHU J R, GU Y L. Impact of seasonal tide variation on salinity intrusion in the Changjiang River Estuary[J]. Chinese Journal of Oceanology and Limnology, 2012, 30(2): 342-351. DOI:10.1007/s00343-012-1115-x |
| [6] |
丁磊, 窦希萍, 高祥宇, 等.长江口盐水入侵研究综述[C]//中国海洋工程学会.第十七届中国海洋(岸)工程学术讨论会论文集(下)中国海洋工程学会, 2015. (DING Lei, DOU Xiping, GAO Xiangyu, et al. The research of saltwater intrusion in Yangtze Estuary[C]//China Ocean Engineering Academy. The 17th China Ocean and Coast Engineering Symposium(volume two), 2015. (in Chinese))
|
| [7] |
丁磊, 窦希萍, 高祥宇, 等. 长江口2013年和2014年枯季盐水入侵分析[J]. 水利水运工程学报, 2016(4): 47-53. ( DING Lei, DOU Xiping, GAO Xiangyu, et al. Analyses of saltwater intrusion in Yangtze estuary in dry season of 2013 and 2014[J]. Hydro-Science and Engineering, 2016(4): 47-53. (in Chinese)) |
| [8] |
WU H, ZHU J R, CHEN B R, et al. Quantitative relationship of runoff and tide to saltwater spilling over from the North Branch in the Changjiang Estuary: A numerical study[J]. Estuarine, Coastal and Shelf Science, 2006, 69: 125-132. DOI:10.1016/j.ecss.2006.04.009 |
| [9] |
陈敏建, 胡雅杰, 马静, 等. 长江口咸潮入侵扩散响应函数及初步应用[J]. 水科学进展, 2017, 28(2): 203-212. ( CHEN Minjian, HU Yajie, MA Jing, et al. Diffusion response function and preliminary application of saltwater intrusion in the Yangtze River Estuary[J]. Advances in Water Science, 2017, 28(2): 203-212. (in Chinese)) |
| [10] |
孙昭华, 严鑫, 谢翠松, 等. 长江口北支倒灌影响区盐度预测经验模型[J]. 水科学进展, 2017, 28(2): 213-222. ( SUN Zhaohua, YAN Xin, XIE Cuisong, et al. An empirical predictive model for saltwater intrusion in the South Branch influenced by tidal flow from the North Branch in the Yangtze River Estuary[J]. Advances in Water Science, 2017, 28(2): 213-222. (in Chinese)) |
| [11] |
唐建华, 徐建益, 赵升伟, 等. 基于实测资料的长江河口南支河段盐水入侵规律分析[J]. 长江流域资源与环境, 2011, 20(6): 677-684. ( TANG Jianhua, XU Jianyi, ZHAO Shengwei, et al. Research on saltwater intrusion of the South Branch of the Changjiang Estuary based on measured date[J]. Resources and Environment in the Yangtze Basin, 2011, 20(6): 677-684. (in Chinese)) |
| [12] |
GU J, HUANG J, HAN B, et al. Numerical study to choose the optimum narrowing schemes for protecting water source in the South Branch of the Changjiang Estuary[C]//3rd International Conference on Bioinformatics and Biomedical Engineering, IEEE, Eng in Medicine and Biology Society of USA, 2009.
|
| [13] |
DING L, DOU X P, GAO X Y, et al. Response of salinity intrusion to winds in the Yangtze Estuary[C]//5th International Conference on Hydraulic Engineering, Hydraulic Engineering V of P.R. China, 2017.
|
| [14] |
DING L, GAO X Y, DOU X P, et al. Research of the influence of salinity intrusion on Qingcaosha water source[C]//5th IAHR World Congress-Managing Water for Sustainable Development, Learning from the Past for the Future IAHR of Malaysia, 2017.
|
2. Nanjing Water Planning and Designing Institute Co., Ltd., Nanjing 210006, China
 2018
2018 