我国拥有漫长的海岸线,包括东部的渤海、黄海、东海以及南部的南海。随着近几年国家经济的快速发展,沿海开发码头、人工岛等大型工程越来越多,体量越来越大,而我国又是受台风袭击较为严重的国家之一,尤其东海、南海沿岸受热带气旋引起的台风灾害严重。如2016年10月我国南部发生的“莎莉嘉”台风导致正在施工的沉箱护岸结构发生严重破坏。经调查发现,施工期沉箱在台风浪作用下发生碰撞破坏是其主要破坏形式。因此,研究台风浪作用下沉箱碰撞破坏模式及破坏机理对提高施工期沉箱抗浪抗撞性能具有重要指导意义。
关于台风浪作用下沉箱的碰撞破坏分析,首先需要确定作用在沉箱结构上的波浪力,现有的Morsion方程[1-2]和绕射波浪理论[3-4]只针对柱体波浪力进行求解,无法求解直立式沉箱结构的波浪力,而《港口与航道水文规范》[5]虽然给出了直立结构上的波浪力分布,但只能确定沉箱上的波浪力大小,要想得到沉箱碰撞过程的运动趋势,必须获得作用在沉箱上的波浪力时程。其次,结构间发生碰撞的时间短,应力波会在结构中传播,导致结构发生非线性变形[6],因此需建立较为精细的有限元模型,准确模拟瞬时碰撞导致结构的破坏效应[7]。传统模拟技术往往需要实现波浪模型和结构模型一体化建模,并实现结构间碰撞效应的模拟,计算量大,计算成本高,或因采用大尺寸有限元网格而降低计算精度[8]。
本文提出一种将台风浪作用下施工期沉箱碰撞反应分析分两步走的数值模拟方法。第一步,利用高精度流体模拟软件Flow-3D的FAVOR网格技术建立流体网格,采用连续性方程和Navier-Stokes方程作为控制方程,通过GMRES(Generalized Minimum RESidual)隐式算法求解压力-速度耦合方程组,获得波浪作用于沉箱结构的波浪力时程; 第二步,建立沉箱结构精细化模型,并将第一步获得的波浪力时程施加于沉箱结构,利用LS-DYNA显式求解器[9]分析波浪作用下沉箱结构间的碰撞反应和破坏过程。将该方法应用于“莎莉嘉”台风引起施工期沉箱的碰撞破坏分析,研究了台风引起的波浪作用方向与沉箱结构碰撞破坏模式之间的关系。
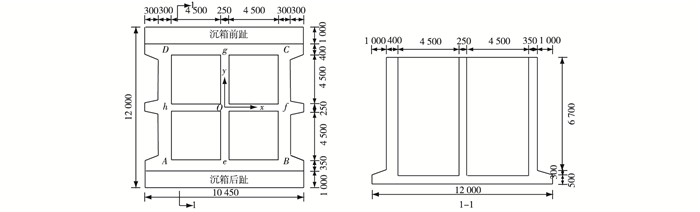
1 “莎莉嘉”台风引起的施工期沉箱碰撞破坏 1.1 工程概况如意岛填海工程位于海口市美兰区北部外海域,利用海域面积为715.75万m2,填海工程护岸采用直立式沉箱结构形式。沉箱并排布置于抛石基床上,2个沉箱平行安装间距为20 cm,沉箱尺寸如图 1所示。设计中沉箱混凝土为C40,钢筋为HRB400,钢筋配筋率为0.8%,工程设计水深为7.35 m。
|
图 1 沉箱尺寸(单位:mm) Figure 1 Caisson sizes(unit: mm) |
2016年10月18日上午第21号台风“莎莉嘉”在海南省万宁市和乐镇沿海登陆,登陆时中心附近最大风力14级,中心最低气压955 hPa。由于无法获得台风发生时所在水域的波浪信息,根据文献[10]的台风特征参数及台风风速预报台风浪波高的回归参数,可得14级台风作用为主导因素的台风浪的有效波高为5.0 m,平均周期为8.8 s。
2016年11月交通运输部天津水运工程科学研究所交通水运工程试验检测中心人员对受损沉箱进行了现场检测,沉箱间碰撞引起的破坏主要表现为4个内隔板Oe,Of,Og,Oh(位置编号见图 1)出现不同程度裂缝,而沉箱4个外壁未发现明显的裂缝破坏。图 2为现场检查发现沉箱内隔板裂缝情况。图 2(a)为沉箱内隔板Oh发生竖向裂缝,图 2(b)为沉箱内隔板Og发生竖向裂缝。同时现场发现裂缝主要集中于内隔板中部和端部节点处。

|
图 2 沉箱内隔板裂缝 Figure 2 Cracks of caisson interior walls |
本文主要研究海南如意岛工程的护岸沉箱结构在“莎莉嘉”台风引起的台风浪作用下结构所受波浪力作用时程。高精度流体模拟软件Flow-3D的造波技术[11]为用户提供了三维波浪力对沉箱结构作用的求解。由于无法获得事故发生时波浪作用方向与沉箱x向(沿沉箱前后壁方向)的夹角,分析时取夹角在0°~90°范围内每隔30°为1种工况,当夹角为90°时波浪力作用方向与沉箱并排方向垂直,导致并排放置的沉箱无法发生碰撞,因此仅考虑3种工况进行分析,分别是波浪作用方向与x向的夹角为0°, 30°, 60°。以波浪作用方向与x方向夹角为0°为例阐述模型的建立过程。应用Flow-3D软件建立三维数值水槽-结构模型,水槽长120 m,宽10 m,高12 m,沉箱前后壁(x向)与水槽入射方向夹角为0°,三维水槽-结构模型如图 3所示。

|
图 3 水槽-结构三维计算模型 Figure 3 3D numerical model for flume-structure |
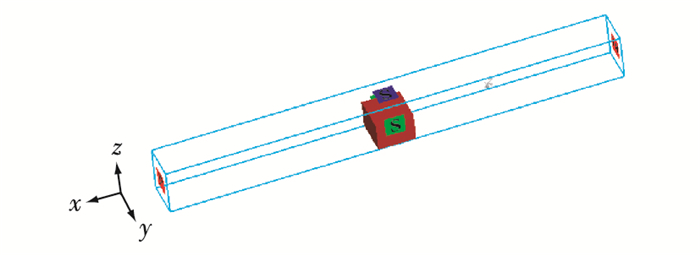
边界条件及初始条件:水槽边界条件设置如图 4所示,水槽前端设置造波(Wave)边界,末端设置静水压力(Specified pressure)边界,水槽底面设为壁面(Wall)边界; 其余各面均设为对称(Symmetry)边界。初始时刻整个水槽中的初始速度为0,压强为沿z向的静水压强,采用静水水面初始化流场。
|
图 4 边界条件示意 Figure 4 Sketch of boundary conditions |
根据事故概况中推算的“莎莉嘉”台风浪的有效波高为5.0 m,平均周期为8.8 s以及设计资料的水深为7.35 m,将波高、周期和水深输入Flow-3D造波系统,可以得到水槽造波如图 5所示。

|
图 5 造波图 Figure 5 Wave generation |
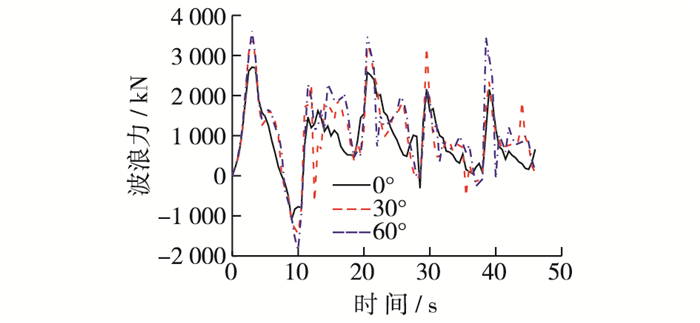
计算时间取5个波浪周期,计算过程中波浪作用于沉箱上发生越浪现象,如图 6所示。通过记录作用于沉箱结构面上的波压力时程可获得沉箱所受波浪力。同理,建立了波浪作用方向与x方向夹角分别为30°,60°的三维水槽-结构模型,通过记录波压力时程曲线获得3种工况下作用于沉箱上的波浪力,如图 7所示。从图 7可以看出,波浪作用方向与x方向夹角为0°,30°,60°的沉箱结构上所受波浪力最大值分别为2 710,3 427和3 613 kN,最大波浪力发生在第1个波峰作用时刻,而后由于波浪发生越浪现象,流体对结构波浪作用力呈现明显的非规则冲击效应; 同时可以看出,随着波浪作用方向与x向夹角的增大,波浪力逐渐增大,其原因是随着夹角的增大,迎水面面积增大从而导致波浪力增大。

|
图 6 波浪发生越浪现象 Figure 6 Overtopping phenomenon |
|
图 7 不同波浪作用与x向夹角的波浪力时程曲线 Figure 7 Wave force time-history curves with different angles between wave direction and x direction |
利用LS-DYNA软件建立2个沉箱的计算模型,沉箱底面设置刚性地基简化模拟抛石基床基础,如图 8所示。采用钢筋混凝土分离式模型来模拟钢筋混凝土沉箱结构,沉箱精细化模型中混凝土采用常应力积分实体单元,钢筋采用Belytschko梁单元,钢筋和混凝土之间采用共节点的方式模拟,不考虑钢筋混凝土之间的粘结滑移效应,钢筋混凝土沉箱有限元模型如图 9所示。为了减小计算成本,设定沉箱B为刚体,重点分析的沉箱A混凝土材料采用损伤本构模型,钢筋采用线性强化本构模型,模型单元尺寸为70 mm。数值分析发现,进一步细化网格只能够有限地提高计算精度,但计算成本成倍增加,甚至会出现计算机的溢出。

|
图 8 沉箱整体模型 Figure 8 Model for caissons |

|
图 9 沉箱精细化有限元模型 Figure 9 Refined finite element model for caisson |
沉箱精细化模型中混凝土材料采用LS-DYNA中的MAT_CONCRETE_DAMAGE_REL3模型,该模型可同时考虑材料的静水压力作用、材料的应变率效应、应力强化效应和材料的残余强度,曾经被成功地用于预测混凝土在冲击荷载作用下单向、双向和三向拉压状态下的响应[12]。同时混凝土材料在碰撞等高加载率荷载作用下,具有显著的应变率效应,其强度可显著提高[13-14],材料的应变率效应一般通过动力增强系数(Dynamic Increase Factor)来考虑。
混凝土强度的动力增强系数采用K & C模型,其抗拉强度的TDIF定义[15]为
| $ {T_{{\rm{DIF}}}} = \left\{ \begin{array}{l} \frac{{{f_{{\rm{td}}}}}}{{{f_{{\rm{ts}}}}}} = \left( {\frac{{{{\dot \varepsilon }_{\rm{d}}}}}{{{{\dot \varepsilon }_{{\rm{ts}}}}}}} \right), {{\dot \varepsilon }_{\rm{d}}} \le 1~~{\rm{}}{{\rm{s}}^{ - 1}}\\ \beta \left( {\frac{{{{\dot \varepsilon }_{\rm{d}}}}}{{{{\dot \varepsilon }_{{\rm{ts}}}}}}} \right), {{\dot \varepsilon }_{\rm{d}}} > 1~~{{\rm{s}}^{ - 1}} \end{array} \right. $ | (1) |
式中:ftd为应变率为
混凝土抗拉强度的CDIF定义为
| $ {C_{{\rm{DIF}}}} = \left\{ \begin{array}{l} \frac{{{f_{{\rm{cd}}}}}}{{{f_{{\rm{cs}}}}}} = \beta {\left( {\frac{{{{\dot \varepsilon }_{\rm{d}}}}}{{{{\dot \varepsilon }_{{\rm{cs}}}}}}} \right)^{1.026\alpha }}, {{\dot \varepsilon }_{\rm{d}}} \le 30~~{{\rm{s}}^{ - 1}}\\ \gamma {({{\dot \varepsilon }_{\rm{d}}})^{1/3}}, {{\dot \varepsilon }_{\rm{d}}} > 30~~{{\rm{s}}^{ - 1}} \end{array} \right. $ | (2) |
式中:fcd为应变率为
钢筋采用LS-DYNA中的MAT_PLASTIC_KINEMATIC模型,其强度的FDIF定义[16]为
| $ {F_{{\rm{DIF}}}} = {(\frac{{\dot \varepsilon }}{{{{10}^{ - 4}}}})^\alpha } $ | (3) |
| $ \alpha = 0.074 - 0.040{f_{\rm{y}}}/414 $ | (4) |
式中:fy为钢筋屈服强度(MPa)。混凝土和钢筋的材料参数见表 1。
| 表 1 材料参数 Table 1 Material parameters |
2个沉箱的碰撞过程需采用接触算法进行模拟,对沉箱与刚性地基间的相互作用以及沉箱间的碰撞反应采用LS-DYNA中CONTACT_AUTOMATIC_SURFACE_TO_SURFACE,沉箱与地基之间的摩擦系数按文献[17]取0.6,沉箱间混凝土的摩擦系数按文献[18]取0.5。
3.2 沉箱碰撞破坏分析通过记录作用于沉箱的波浪力时程曲线,将所记录的波浪力时程曲线编写成LS-DYNA的模型输入文件,并分别按波浪力与x向夹角为0°,30°,60°共3种工况施加于所建立的沉箱B重心上,模拟波浪入射方向与x向成不同夹角时沉箱结构的碰撞反应。
采用上述数值模拟方法模拟了3种工况下沉箱的碰撞破坏模式。图 10给出了波浪作用方向与x方向夹角分别为0°,30°,60°对应3种工况a,b,c下沉箱的碰撞破坏模式。可见,3种不同的波浪与沉箱作用方向引起沉箱碰撞破坏模式与破坏程度不尽相同。在工况a中,沉箱B与沉箱A沿0°发生碰撞,沉箱外壁AD和BC发生了严重破坏,在外壁节点处和中部出现了严重的裂缝破损。同时,内隔板Oe和Og发生了严重破坏,内隔板Of,Oh未发现明显裂缝破损,内隔板g,e,O节点处和板中部出现了严重的裂缝破损。在工况b中,沉箱B与沉箱A沿30°发生斜向碰撞,沉箱外壁AD和BC发生了较为严重的破坏,内隔板Oe,Og发生了严重的裂缝破坏,内隔板Of,Oh也发生了轻微的裂缝破损,其破坏程度较内隔板Oe和Og轻,内隔板g,e,O节点处和板中部出现了严重的裂缝破损,可以看出内隔板中部和节点处的破损现象与图 2(b)所示破坏模式相近。在工况c中,沉箱B与沉箱A沿60°发生斜向碰撞,沉箱4个外壁的破损程度较小,4个内隔板的破坏模式与工况b相似,但内隔板Oe和Og破损程度较工况b轻,内隔板Of和Oh的破损程度与工况a和b相比最严重。出现该现象的原因是波浪作用方向与x向的夹角就越小,沉箱B与沉箱A发生碰撞时的夹角就越小,此时内隔板Oe和Og所受x方向惯性力越大,易引起内隔板中部和端部发生破坏,而此时内隔板Of和Oh所受y方向的惯性力越小,越不容易发生破损。

|
图 10 沉箱B与A沿不同角度碰撞的破坏模式 Figure 10 Pounding damage mode of caissons with different angles between caissons B and A |
综上所述,当波浪作用方向与x向夹角为60°时,沉箱破坏模式与现场检查的结果相近,即沉箱外壁未发生明显破坏,内隔板发生不同程度的裂缝破损。值得注意的是,现场无法获得实际波浪作用与沉箱夹角数据,假定波浪作用方向与x向夹角为0°,30°,60°共3种工况进行计算,数值分析表明夹角为60°时其模拟结果与现场情况相近,但并不代表实际波浪作用方向与沉箱夹角为60°。
4 结语提出了一种基于台风浪作用下施工期沉箱碰撞反应分析分两步走的数值模拟方法,并将该方法应用于“莎莉嘉”台风引起施工期沉箱碰撞破坏分析研究。通过数值分析,得出如下结论:
(1) 所提出的方法可以模拟施工期沉箱在台风浪作用下的碰撞反应,不同波浪作用方向引起沉箱发生不同角度的碰撞会导致沉箱不同的碰撞破坏模式。
(2) 所模拟的3种工况中波浪作用方向与x向夹角成60°时,沉箱碰撞破坏模式与“莎莉嘉”台风作用期间的现场情况更为接近,沉箱外壁未发生明显破坏,内隔板出现不同程度的裂缝破损。
| [1] |
李玉成, 滕斌. 波浪对海上建筑物的作用[M]. 北京: 海洋出版社, 2002: 121. ( LI Yucheng, TENG Bin. Wave action on maritime structures[M]. Beijing: China Ocean Press, 2002: 121. (in Chinese))
|
| [2] |
TERRO M J, ABDEL-ROHMAN M, TERRO M J. Wave induced forces in offshore structures using linear and nonlinear forms of Morison's equation[J]. Journal of Vibration and Control, 2007, 13(2): 139-157. DOI:10.1177/1077546307067085 |
| [3] |
BAO W G, FUJIHASHI K, KINOSHITA T. Interaction of a submerged elliptic plate with waves[J]. Journal of Hydrodynamics, 2010, 22(5): 77-82. DOI:10.1016/S1001-6058(09)60173-6 |
| [4] |
李忠献, 黄信. 地震和波浪联合作用下深水桥梁的动力响应[J]. 土木工程学报, 2012, 45(11): 134-140. ( LI Zhongxian, HUANG Xin. Dynamic responses of bridges in deep water under combined earthquake and wave actions[J]. China Civil Engineering Journal, 2012, 45(11): 134-140. (in Chinese)) |
| [5] |
JTS 145—2015港口与航道水文规范[S]. (JTS 145—2015 Code of hydrology for harbor and waterway[S]. (in Chinese))
|
| [6] |
GUO Anxin, LI Zhongjun, LI Hui. Point-to-surface pounding of highway bridges with deck rotation subjected to bi-directional earthquake excitations[J]. Journal of Earthquake Engineering, 2011, 15(2): 274-302. DOI:10.1080/13632461003739730 |
| [7] |
BI K, HAO H. Numerical simulation of pounding damage to bridge structures under spatially varying ground motions[J]. Engineering Structures, 2013, 46(1): 62-76. |
| [8] |
丁阳, 汪明, 李忠献. 爆炸荷载作用下钢框架结构连续倒塌分析[J]. 建筑结构学报, 2012, 33(2): 78-84. ( DING Yang, WANG Ming, LI Zhongxian. Numerical analysis of damage and collapse process of steel frame structures under blast loads[J]. Journal of Building Structures, 2012, 33(2): 78-84. (in Chinese)) |
| [9] |
Livermore Software Technology Corporation. LS-DYNA user manual[Z]. 2007.
|
| [10] |
方钟圣, 金承仪. 日本浮标站台风浪波高与风速等参数的统计分析[J]. 船舶力学, 2003, 7(5): 1-10. ( FANG Zhongsheng, JIN Chengyi. Statistical analysis of wave height, wind speed and other parameters due to tropical cyclones in the Northwest Pacific area[J]. Journal of Ship Mechanics, 2003, 7(5): 1-10. DOI:10.3969/j.issn.1007-7294.2003.05.001 (in Chinese)) |
| [11] |
张婷.波浪的三维数值模拟及其应用[D].天津: 天津大学, 2009. (ZHANG Ting. Three-dimensional numerical simulation of waves and its application[D]. Tianjin: Tianjin University, 2009. (in Chinese))
|
| [12] |
师燕超, 李忠献, 郝洪. 爆炸荷载作用下钢筋混凝土框架结构的连续倒塌分析[J]. 解放军理工大学学报(自然科学版), 2007, 8(6): 652-658. ( SHI Yanchao, LI Zhongxian, HAO Hong. Numerical analysis of progressive collapse of reinforced concrete frame under blast loading[J]. Journal of PLA University of Science and Technology, 2007, 8(6): 652-658. (in Chinese)) |
| [13] |
MALVAR L J, ROSS C A. A review of strain rate effects for concrete intension[J]. Aci Materials Journal, 1998, 95(6): 735-739. |
| [14] |
BISCHOFF P H, PERRY S H. Compressive behavour of concrete at high strain rates[J]. Materials and Structures, 1991, 24(6): 425-450. DOI:10.1007/BF02472016 |
| [15] |
师燕超.爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D].天津: 天津大学, 2009. (SHI Yanchao. Dynamic response and damage mechanism of reinforced concrete structures under blast loading[D]. Tianjin: Tianjin University, 2009. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10056-2010090306.htm
|
| [16] |
MALVAR L J. Review of static and dynamic properties of steel reinforcing bars[J]. Aci Materials Journal, 1998, 95(5): 609-616. |
| [17] |
JTS 167-2—2009重力式码头设计与施工规范[S]. (JTS 167-2—2009 Design and construction code for gravity quay[S]. (in Chinese))
|
| [18] |
BI K, HAO H. Numerical simulation of pounding damage to bridge structures under spatially varying ground motions[J]. Engineering Structures, 2013, 46(1): 62-76. |
 2018
2018 