2. 西安市水利规划勘测设计院,陕西 西安 710054
城市人工湖是城市公众休闲娱乐、亲近自然的场所,具有调节小气候、净化水质、维持生物多样性等生态功能。城市人工湖具有水浅,流动性差、底泥污染严重,以及接纳混杂污水的特点,导致水质受到污染,水体富营养化严重。湖泊水动力过程对湖泊中物质、能量的输移扩散起着决定性作用,是研究泥沙、水质和生态等的基础[1-2],其水动力与湖体本身的形态、吞吐流、风场和水位等物理参数有关[3],其中湖泊水位是影响湖泊水文过程和生态环境的主要因素[4]。
人工调控性湖泊主要是对入湖流量的调控,自然要素只能对入湖流量产生影响。对于功能性湖泊,如灌溉、防洪、供水和净化水质等,入湖流量是最终影响水位及其变差范围和时空变化特征的决定性因子[5]。目前,国内外学者通过建立二维、三维浅水动力学模型[6-8],研究湖泊水动力过程的特征及形成机制,较多关注风场、吞吐流和湖底地形等要素对湖泊水动力的影响[9-12],常常忽略水位的变化。
水位是湖泊贮水量变化的度量,对于湖泊生态系统而言,存在一个适宜的水位[13]。研究者主要针对湖泊水位变动对水生植被影响方面取得了一定进展,包含对天然大型湖泊水位变动的范围[14-15]、发生时间等其他规律的研究[16-18],但未涉及对水动力影响的研究。天然湖泊水位一般在年内随季节变化,而人工湖水位则受人为调控。由于人工湖受人为调控的水位变化特别明显,水位调控是湖泊生态恢复与管理的重要技术[7],因此研究水位对人工湖泊水动力的影响很有必要。
1 研究方法和方案设计 1.1 水动力模型原理由于人工湖水平尺度远大于垂直尺度,采用二维水动力模型。模型基于不可压缩和雷诺值平均分布的N-S方程,并服从于Boussinesq假定和静水压力的假定[19]。二维浅水方程为:
| $ \partial \varphi /\partial t + \partial p/\partial x + \partial q/\partial y = S $ | (1) |
| $ \begin{array}{l} \frac{{\partial p}}{{\partial t}} + \frac{\partial }{{\partial x}}\left( {\frac{{{p^2}}}{h}} \right) + \frac{\partial }{{\partial y}}\left( {\frac{{pq}}{h}} \right) + gh\frac{{\partial \varphi }}{{\partial x}} + \frac{{gp\sqrt {{p^2} + {q^2}} }}{{{C^2}{h^2}}} - \frac{1}{{{\rho _{\rm{w}}}}}\left[ {\frac{\partial }{{\partial x}}(h{\tau _{xx}}) + \frac{\partial }{{\partial y}}(h{\tau _{xy}})} \right] - \\ \mathit{\Omega} q - {\tau _{\rm{s}}}{V_x} + \frac{h}{{{\rho _{\rm{w}}}}}\frac{\partial }{{\partial x}}{p_{\rm{a}}} = {S_x} \end{array} $ | (2) |
| $ \begin{array}{l} \frac{{\partial q}}{{\partial t}} + \frac{\partial }{{\partial y}}\left( {\frac{{{q^2}}}{h}} \right) + \frac{\partial }{{\partial x}}\left( {\frac{{pq}}{h}} \right) + gh\frac{{\partial \varphi }}{{\partial y}} + \frac{{gq\sqrt {{p^2} + {q^2}} }}{{{C^2}{h^2}}} - \frac{1}{{{\rho _{\rm{w}}}}}\left[ {\frac{\partial }{{\partial y}}(h{\tau _{yy}}) + \frac{\partial }{{\partial x}}(h{\tau _{xy}})} \right] - \\ \mathit{\Omega} p - {\tau _{\rm{s}}}{V_y} + \frac{h}{{{\rho _{\rm{w}}}}}\frac{\partial }{{\partial y}}{p_{\rm{a}}} = {S_y} \end{array} $ | (3) |
式中:φ为高程(m); p, q分别为沿x和y方向的单宽流量(m2/s); Vx, Vy分别为沿x, y方向的风速(m/s); h为水深(m); C为Chezy阻力系数(m1/2/s); g为重力加速度(m/s2); τs为风摩擦系数; Ω为科氏力系数,受维度影响(1/s); pa为大气压强(Pa); ρw为水密度(kg/m3); S, Sx, Sy分别为源质量的动量和沿x,y方向的动量分量(kg·m/s); τxx,τxy,τyy为不同方向的有效剪切应力; x, y为空间坐标(m); t为时间(s)。
针对人工湖数值计算面临复杂几何地形和不规则边界的问题,建立非结构化三角形网格下的二维水动力模型,将任意三角形作为计算单元,采用单元中心的有限体积法求解,有Ros's近似黎曼法求解单元界面的对流流动,使用二阶TVD格式的限制器函数避免数值震荡。
1.2 研究区域雁鸣湖地处干旱半干旱地带,湖泊供水由浐河提供,四季供水量变化明显,其中雁鸣湖5号属于小型浅水湖泊,面积不大,形状不规则,东西宽300 m(为x方向),南北长1 200 m(为y方向,以西安80为基准坐标),位于浐河旁边,属于河道型湖泊,目前湖泊污染较严重。浐河多年平均最小流量0.286 m3/s,水流瞬时流量0.235~0.450 m3/s,满足浐河补给雁鸣湖设计流量0.2 m3/s要求。雁鸣湖正常蓄水位434.5 m,最低水位433 m,水深1.5~2.0 m。采用非结构三角形网格对湖泊区域进行划分,其中网格数8 084个,节点数3 421个,地形采用加权反离法插值到每个网格节点。非结构网格能对复杂几何地形提供最优程度的拟合。为了更好地拟合边界处的地形变化,对湖岸边界附近进行网格加密和光滑处理,如图 1所示。流速测点布置见图 2。

|
图 1 湖泊网格划分和地形 Figure 1 Model grids and bathymetry of lake |

|
图 2 流速测点分布 Figure 2 Velocity measurement points |
时间步长的设定是模型稳定运行的关键,必须保证CFL数小于1,对于笛卡尔坐标系下的浅水方程式为:
| $ {\rm{CFL}} = \left( {\sqrt {gh} + |u|} \right)\frac{{\Delta t}}{{\Delta x}} + \left( {\sqrt {gh} + |v|} \right)\frac{{\Delta t}}{{\Delta y}} $ | (4) |
式中:h为水深(m); u和v分别为x和y方向流速分量(m/s); g为重力加速度(m/s2); Δx和Δy分别为x和y方向特征长度,Δx和Δy近似于三角形网格的最小边长,以三角形网格中心为水深和流速的取值点; Δt为时间间距。
1.4 边界条件湖泊的边界条件分别为闭合边界、开边界和干湿边界。闭合边界指所有正交于边界流动变量为0的边界,对应于湖泊的陆地边界。开边界指有随时间变化的量的边界,对于湖泊为进出水口的流量过程和水位过程。干湿边界处理动边界问题,避免强浅水效应,对计算区域内水位变化过程,当退水水深小于0.005 m时,令该网格点为“干点”,不参与水动力计算; 当水深大于0.005 m但小于0.05 m时,该网格点仅参与水流连续方程的计算; 当水深大于0.1 m时,令该网格点为“湿点”,参与水流连续方程和动量方程的计算。对于雁鸣湖水位变化的动边界,采用“干湿判别法”处理计算。
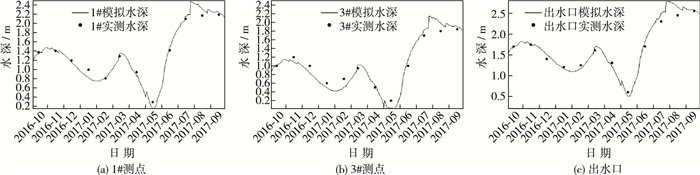
1.5 模型验证该模型水位、流量和流场等水动力指标参数已在2007—2009年进行了全面率定和验证[20],表明模型具有关键过程模拟的优势和能力。此处对2016年10月至2017年9月的水动力过程进行进一步验证,选择湖区1#和3#及出水口(见图 2)实测水深变化过程进行验证(图 3),同时计算误差指标:平均相对误差(MAE)、均方根误差(RMSE)、决定系数(r2)、纳什效率系数(NSE),误差指标分别为:0.034 4~0.854 0,0.068 4~0.854 2,0.913 2~0.954 4,0.933 8~0.975 9。对比曲线趋势和误差指标统计可以看出,模型模拟精度较好,能真实反映雁鸣湖水动力变化过程。水位较高时,整体模拟效果好于低水位,这是因为较高水位时湖泊湖面较大,流场稳定,低水位时受湖泊地形影响,流场受到一定程度阻滞作用,从而模拟误差较大。
|
图 3 模型验证 Figure 3 Model validation |
根据雁鸣湖调控换水调研结果,每年3月为湖泊正常水位,4月湖泊放水,且无引水补给,水位下降明显,5月在低水位下,开放进出口闸门,引入浐河水源对湖底沉积物进行冲刷,6月进行引水补给,达到正常水位。湖泊的进出流均为缓流,主要影响附近局部水域的流速变化[3],对湖泊整体流速的影响可忽略不计。设计模拟方案见表 1。
| 表 1 模拟方案 Table 1 Model simulation schemes |
模拟方案主要考虑单因素水位对湖泊流速的影响,其中湖泊进出流量为0.2 m 3/s,风向为恒定常年主导风、风速为年平均风速,不考虑降雨和蒸发。作为对比增加实测换水工况模拟,分析水位和流速时空分布的影响,实测工况中水文和气象数据在2017-03-01—2017-06-30实测得到,水文数据包括实测湖泊进出口流量(m3/s)和监测点水位数据(m); 气象数据来自国家气象中心西安站(ID:57131),气象数据包括降雨(mm)、蒸发(mm)、温度(℃)、风速(m/s)和风向。湖泊模拟的地形数据由西安市水利规划勘测设计院提供。
2 结果与讨论水位变化是湖泊流场影响因素之一,特别是人工湖泊水位变化明显,对于湖泊的影响更加显著,根据模拟方案和实测换水工况探讨水位对人工湖水动力的影响。
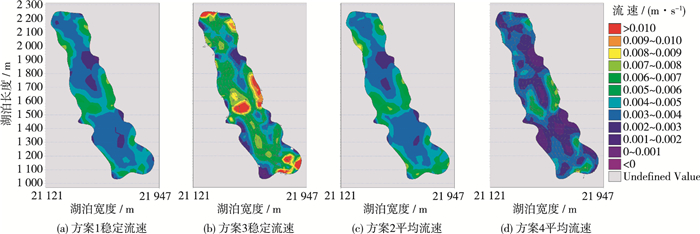
2.1 模拟结果分析图 4为模拟结果,分别给出了高低水位流速稳定时的流速分布与水位升高和降低过程中的湖泊平均流速分布。当湖泊处于不同水位时,湖泊的流速差别较大,低水位湖泊流速大于高水位,但环流分布形态影响较少。正常蓄水位时,湖泊边界凹区域和环流过渡区形成死水区; 低水位时,由于湖底地形作用在湖底低洼处形成高速流域,并且在进出口区域由于水位顶托作用的减弱也形成高速流域,因而湖泊整体流速增大。在湖泊水位升高或降低过程中,湖泊的平均流速分布相近,高流速分布区域相近,相对水位升高或降低,流速在进水口和出水口差别较大(因为湖泊水位变化主要由进出水口流量不同引起,所以导致湖泊流速的差异)。
|
图 4 不同方案的流速分布 Figure 4 Distribution of flow velocities under different schemes |
为了说明水位对湖泊流速的影响,取了湖中不同位置的月平均流速值(图 5)来说明水位的影响程度,其中1#和3#是环流点位置,2#和4#是无环流点位置。由图 5可见,湖泊不同位置点的流速存在差异,同一位置点不同水位下的流速也存在差异。在正常水位下湖泊的流速最小,在低水位下流速最大,水位变化下平均流速介于两者之间,说明低水位有利于湖泊流场,但是作为城市人工湖泊,水位太低,不能满足生态环境的需求,达不到生态景观的水位要求,所以湖泊不可以长时间低水位运行。

|
图 5 湖泊不同位置的月均流速 Figure 5 Monthly average velocities of different points in Yanming Lake |
基于雁鸣湖水动力模型输出的水位和水深时空分布如图 6所示。3月份整个湖泊保持较高水位,空间差异不明显,湖面近似水平,湖泊高水位使水面相应增大,湖泊水位对补水的顶托作用,致使湖水水面较平,水深空间分布直接受湖底地形的影响,自上游至下游呈逐级递增趋势,出水口的水深最深,局部区域水深接近2 m,湖泊中心到边界水深由深到浅。4月份湖泊水位出现明显的水位梯度,水位自上游逐级降低,水域范围有收缩态势,水深变化明显。5月湖泊水位达到最低,河滩裸露,水位变化梯度达到最大,水位差约1 m。因水位不断下降直至湖水归槽,部分湖流近似河流特性,水位因湖底坡降作用而变化,上游大部分区域水深极小,呈现裸露状态; 部分区域形成独立的水域。6月份水位出现梯度变化,水深增大,水域范围呈扩大态势,水位达到正常水位。总体来说,湖泊在3月和5月时水位分布相对稳定,部分差异由湖底地形造成; 在4月和6月湖泊水位分布从上游至下游呈梯度变化,且湖泊长宽比较大,属狭长型湖泊,因而湖面比降较大。

|
图 6 湖泊水位、水深时空分布 Figure 6 Temporal and spatial variation of water level and depth in Yanming Lake |
湖泊流速受地形、吞吐流、风场、水位等因素影响。根据实测换水水位的变化过程和实测风场及吞吐流,分析模拟结果(如图 7)可得:3月湖泊水位较高,湖泊流速较小(0.002 m/s左右),高水位使湖泊呈现典型湖相; 4月湖泊水位下降,湖泊流速加快(0.005 m/s左右),并且湖泊受降雨和风场的影响较大; 5月湖泊水位达到最低,湖泊流场为河相流场,由于湖泊地形的影响因素增加,其动力结构更复杂,流速达到最大(0.007 m/s左右); 6月湖泊水位上升,流速减小(0.003 m/s左右)。水位变化过程中湖泊形成的相对高流速区的位置基本不变,环流作用区域和进水口区域平均流速相对较高,水位变化过程的平均流速相对大于正常水位的湖泊流速,水位的升高或降低过程实际是湖泊流场的湖相和河相相互转化过程。

|
图 7 雁鸣湖流场分布 Figure 7 Spatial variation of flow field in Yanming Lake |
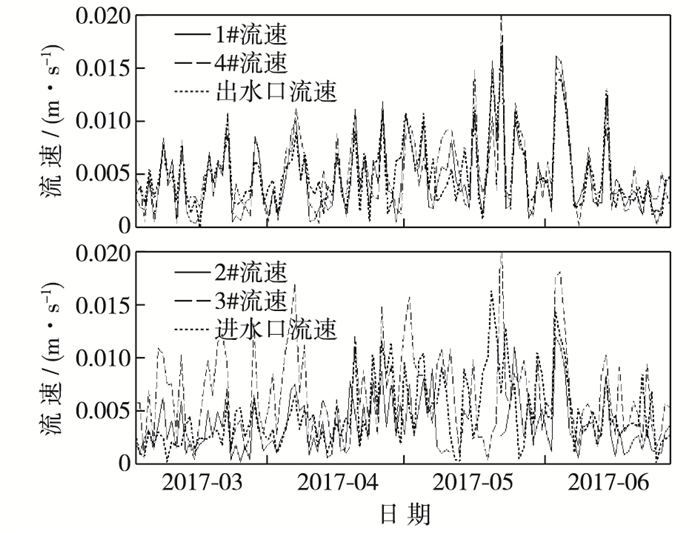
各采样点在连续水位变化下,流速变化见图 8。由图可见,相对正常水位下(3月)各测点整体流速最小; 低水位(5月)时流速最大; 其次是水位变化下(4月和6月)的流速。分析实测资料可知,湖泊水动力是多因素综合作用的结果,不同因素作用随时间变化造成流速随时间变化,不同位置多因素综合作用导致湖泊流速的差异。在低水位情况下各点流速相近,变化不明显; 3#点流速较大,且流速变化明显,究其原因是3#处于环流作用处; 实际情况下,变化风场的作用导致流速的瞬时增大,例如6月初湖泊流速突然增大,其他各点流速变化趋势相近。
|
图 8 水位变化下日均流速变化 Figure 8 Changes in daily average velocities during water level fluctuations |
针对雁鸣湖单因素水位和换水期间水位变化对流场进行模拟,结果表明水位对湖泊水动力有一定影响。随着湖泊水位降低,水体体积、质量减少,需要的外界驱动力减弱,因而在相同的驱动力下湖区流速有所增加[21]。对补水水位升高而言,水面升高产生顶托作用随接触面积增大而增大; 而在风力保持不变的前提下,顶托作用使得补水驱动力无法满足水体运动需要,因而整个湖区的流速便会降低[11]。另外,环流形成方式随着水位变化而变化,在正常水位下主要由风作用形成湖流,但水位较低时湖底地形和吞吐流作用增强共同形成与风向相同的补偿流,从而使湖流形式复杂,环流之间相互作用使得流速增加。水位不是单独对水动力产生影响,而是多种湖泊驱动力共同作用的结果,不同水位通过外界驱动力对湖泊水动力产生影响,因此湖泊保持一定水位有利于湖泊水动力的改善。
水位对人工湖生态有重要影响,若水位变化不适当,则会带来负面影响,长期固定的高或低水位使湖泊多样性降低[18]。人工湖在满足景观生态蓄水的要求下,增加水位变化既有利于水生态,也有利于湖泊水动力改善。因此,可以通过调节人工湖进出湖的流量使水位变化,从而改善生态和水动力环境。
3 结语基于二维水动力模型,模拟雁鸣湖2017年3—6月期间的水动力变化过程,探究单因素水位对湖泊流场影响,以及换水期间水位和流场的时空分布特征,结论如下:
(1) 水位是湖泊水动力影响因素之一。不同水位及其变化过程情况下,湖泊流速存在差异,低水位时湖泊平均流速大于正常水位时,水位降低和升高过程中湖泊平均流速介于两者之间; 随着水位降低,环流的形成越复杂。
(2) 换水期间水位和流速分布存在差异。3月份湖泊处于较高水位期,湖区水位空间分布差异较小,水深自上游至下游呈逐级递增趋势,湖泊流速最小; 4月和6月份水位出现明显差异,水深变化明显,湖泊平均流速大于3月份流速; 5月份为低水位期,河滩裸露,水深空间分布差异较大,湖泊流速最大,验证了单因素水位对湖泊流速的影响。
(3) 湖泊不同水位对流速大小及其分布影响有所不同,在保持生态景观水位前提下,人工湖水位变化有利于改善湖泊水动力。
| [1] |
姚静, 张奇, 李云良, 等. 定常风对鄱阳湖水动力的影响[J]. 湖泊科学, 2016, 28(1): 225-236. ( YAO Jing, ZHANG Qi, LI Yunliang, et al. The influence of uniform winds on hydrodynamics of Lake Poyang[J]. Journal of Lake Sciences, 2016, 28(1): 225-236. (in Chinese)) |
| [2] |
钟小燕, 王船海, 庾从蓉, 等. 流速对太湖河道底泥泥沙、营养盐释放规律影响实验研究[J]. 环境科学学报, 2017, 37(8): 2862-2869. ( ZHONG Xiaoyan, WANG Chuanhai, YU Congrong, et al. Characteristics of sediments and nutrient release under different flow velocity[J]. Acta Scientiae Circumstantiae, 2017, 37(8): 2862-2869. (in Chinese)) |
| [3] |
姜恒志, 崔雷, 石峰, 等. 风场、地形和吞吐流对太湖流场影响的研究[J]. 水力发电学报, 2013, 32(6): 165-171. ( JIANG Hengzhi, CUI Lei, SHI Feng, et al. Study on influences of wind field, topography and inflow/outflow on flow in Lake Tai[J]. Journal of Hydroelectric Engineering, 2013, 32(6): 165-171. (in Chinese)) |
| [4] |
NGES A. The effect of extreme water level decrease on hydrochemistry and phytoplankton in a shallow eutrophic lake[J]. Hydrobiologia, 1999, 409: 277-283. |
| [5] |
COOPS H, BEKLIOGLU M, CRISMAN T L. The role of water-level fluctuations in shallow lake ecosystems-workshop conclusions[J]. Hydrobiologia, 2003, 506-509(1-3): 23-27. DOI:10.1023/B:HYDR.0000008595.14393.77 |
| [6] |
OPDYKE D. Hydrodynamics and water quality modeling: modeling rivers, lakes, and estuaries[M]. Wiley-Interscience, 2008: 366-366.
|
| [7] |
AI Congfang, JIN Sheng, LV Biao. A new fully non-hydrostatic 3D free surface flow model for water wave motions[J]. International Journal for Numerical Methods in Fluids, 2011, 66(11): 1354-1370. DOI:10.1002/fld.v66.11 |
| [8] |
郑婷婷, 徐明德, 景胜元, 等. 汾河水库水动力及水质数值模拟[J]. 水利水运工程学报, 2016(3): 105-113. ( ZHENG Tingting, XU Mingde, JING Shengyuan, et al. Simulation of hydrodynamics and water quality for Fenhe reservoir[J]. Hydro-Science and Engineering, 2016(3): 105-113. (in Chinese)) |
| [9] |
WU Z, HE H, CAI Y, et al. Spatial distribution of chlorophyll a and its relationship with the environment during summer in Lake Poyang: a Yangtze-connected lake[J]. Hydrobiologia, 2014, 732(1): 61-70. DOI:10.1007/s10750-014-1844-2 |
| [10] |
GAO F, FENG M Q, HAN S X, et al. Numerical simulation research on flow characteristics and influential factors of Wuxing Lake[J]. International Journal of Heat and Technology, 2016, 34(1): 80-88. DOI:10.18280/ijht |
| [11] |
ANDERSON E J, SCHWAB D J. Relationships between wind-driven and hydraulic flow in Lake St. Clair and the St. Clair River Delta[J]. Journal of Great Lakes Research, 2011, 37(1): 147-158. DOI:10.1016/j.jglr.2010.11.007 |
| [12] |
RAZMI A M, BARRY D A, BAKHTYAR R, et al. Current variability in a wide and open lacustrine embayment in Lake Geneva (Switzerland)[J]. Journal of Great Lakes Research, 2013, 39(3): 455-465. DOI:10.1016/j.jglr.2013.06.011 |
| [13] |
刘永, 郭怀成, 周丰, 等. 湖泊水位变动对水生植被的影响机理及其调控方法[J]. 生态学报, 2006, 26(9): 3117-3126. ( LIU Yong, GUO Huaicheng, ZHOU Feng, et al. Role of water level fluctuation on aquatic vegetation in lakes[J]. Acta Ecologica Sinica, 2006, 26(9): 3117-3126. DOI:10.3321/j.issn:1000-0933.2006.09.042 (in Chinese)) |
| [14] |
齐凌艳, 黄佳聪, 高俊峰, 等. 鄱阳湖枯水水位及流速时空分布模拟[J]. 长江流域资源与环境, 2017, 26(4): 572-584. ( QI Lingyan, HUANG Jiacong, GAO Junfeng, et al. Temporal and spatial simulation of water level and velocity during low water level statistical year in Lake Poyang[J]. Resources and Environment in the Yangtze Basin, 2017, 26(4): 572-584. DOI:10.11870/cjlyzyyhj201704010 (in Chinese)) |
| [15] |
GARCÍA DE EMILIANI M O. Effects of water level fluctuations on phytoplankton in a river-floodplain lake system (Parana River, Argentina)[J]. Hydrobiologia, 1997, 357(1-3): 1-15. |
| [16] |
姚鑫, 杨桂山, 万荣荣, 等. 水位变化对河流、湖泊湿地植被的影响[J]. 湖泊科学, 2014, 26(6): 813-821. ( YAO Xin, YANG Guishan, WAN Rongrong, et al. Impact of water level change on wetland vegetation of rivers and lakes[J]. Journal of Lake Sciences, 2014, 26(6): 813-821. (in Chinese)) |
| [17] |
LENSSEN J P M, MENTING F B J, PUTTEN W H V D, et al. Effects of sediment type and water level on biomass production of wet land plant species[J]. Aquatic Botany, 1999, 64(2): 151-165. DOI:10.1016/S0304-3770(99)00012-1 |
| [18] |
HEBB A J, MORTSCH L D, DEADMAN P J, et al. Modeling wetland vegetation community response to water-level change at Long Point, Ontario[J]. Journal of Great Lakes Research, 2013, 39(2): 191-200. DOI:10.1016/j.jglr.2013.02.001 |
| [19] |
D HI. MIKE 21 Flow model: hydrodynamic module scientific documentation[M]. Denmark: Danish Hydraulic Institute, 2007.
|
| [20] |
路璐.城市景观湖泊水动力学模拟研究——以西安浐灞雁鸣湖2号湖为例[D].西安: 西安理工大学, 2012. (LU Lu. Urban landscape lake water dynamics study—Xi'an Chanba Yanming 2nd Lake for example[D]. Xi'an: Xi'an University of Technology, 2012. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y2118164
|
| [21] |
田泽斌, 王丽婧, 郑丙辉, 等. 城陵矶综合枢纽工程建设对洞庭湖水动力影响模拟研究[J]. 环境科学学报, 2016, 36(5): 1883-1890. ( TIAN Zebin, WANG Lijing, ZHENG Binghui, et al. Impact simulation of the Chenglingji hydraulic project on hydrodynamics of Dongting Lake[J]. Acta Scientiae Circumstantiae, 2016, 36(5): 1883-1890. (in Chinese)) |
2. Xi'an Water Conservancy Survey and Design Institute, Xi'an 710054, China
 2018
2018 
