北方缺水地区平原河道上的多孔节制闸或蓄排兼用水闸,除在汛期可能全部开闸放水外,多数情况为少数孔局部开启运用,闸后为流态复杂的三元水流,但现行的水闸设计规范仍推荐按二元水跃问题计算和设计消能设施[1],河北吴桥,山东辛集、庆云等不少水闸工程均因这种二元设计三元运行受到冲刷破坏[2-3]。究其原因是由于多孔水闸少数孔开启时主流出闸后经两侧静水挤压产生水跃,随后在消力池后发生扩散继而在海漫上形成二次水跃,冲刷河床[4-5]。
对于这种多孔水闸少数孔开启引起的三元突扩水跃及二次水跃问题,在闸后消力池内设置导流墙来改善主流被挤压而形成的恶劣流态是有效的改进措施[6-8],可适应多孔水闸分区运用的方式,提高消能率, 在每一分区内使跃前受挤压部分产生平面流态。河北吴村闸曾采用与池长相等的全长导流墙; 李华等针对每孔净宽8 m的10孔闸(平板闸门)通过试验建议隔3孔采用池长75%的导流墙[7];龚彦奎等针对每孔净宽10 m的9孔闸通过1:60的整体模型试验(弧形闸门)后指出:在综合式消力池内隔3孔设置消力池长50%~60%长度的导流墙,既可防止主流在池中前部受到挤压, 又不妨碍池尾部的扩散,从跃后水深和海漫上的水流流态看,其效果优于不设导流墙以及设全长导流墙的情况。以上试验研究对导流墙长度的建议值不一致,而且对消力池(坎)后二次水跃的特性研究不够充分。事实上,二次水跃对海漫及下游河道的冲刷破坏是造成一些水闸失事的直接原因。本文拟采用物理模型试验与数值模拟相结合的方法,研究导流墙长度对跃后水深及二次水跃的影响,找出最佳导流墙长度,为相似工程设计与运行管理提供借鉴和参考。
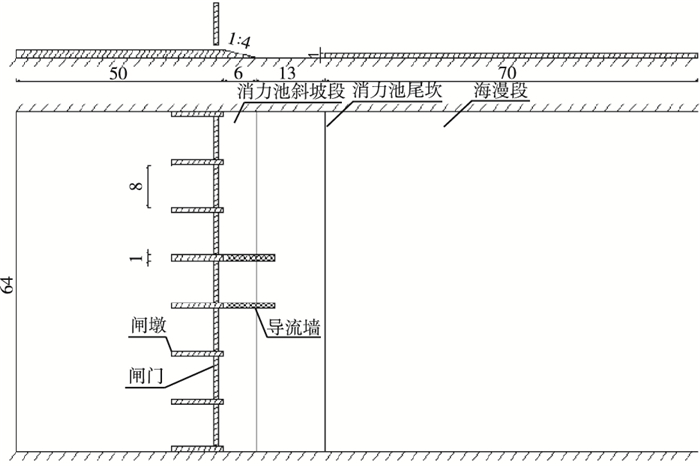
1 试验设计模型按照重力相似准则设计,以某拦河闸为原型,综合考虑场地及其他试验条件等因素,设计了7孔平板水闸整体模型。此模型采用几何比尺λL为1:100正态模型,其他参数比尺为:流量比尺λQ =λL5/2=100 000;流速比尺λV =λL1/2=10,糙率比尺λn =λL1/6=2.15。试验模型闸孔宽8 cm,采用下降式消力池,池长Ls为19 cm,池深1 cm,消力池斜坡段坡度为1:4,具体尺寸见图 1。
|
图 1 水闸试验模型纵剖面及平面(单位:cm) Figure 1 Vertical profile and plan of sluice test model (unit: cm) |
北方平原河道上的水闸经常以单孔开启或3孔开启泄放中小流量,或者以单孔、部分孔先开一定开度,然后由中间孔向两侧分段分区对称启闭[1, 7],分别对中间单孔和连续3孔开启时的闸后流态进行分析。
设计试验条件控制上游水深为7 cm; 闸门开度为1 cm; 单孔和连续3孔开启时下游水深分别为1和2 cm,对消力池内导流墙长度为消力池长度的50%, 60%, 75%和100%时进行对比试验。
2 数值模型 2.1 控制方程采用Naiver-Stokes方程,建立RNG k-ε紊流计算模型来解决这种具有典型空间突扩式三元水力特性的紊流运动问题。控制方程如下:
| $ 连续方程:\;\;\;\;\frac{{\partial {u_i}{A_i}}}{{\partial {x_i}}} = 0 $ | (1) |
| $ {\rm{动量方程:}}\;\;\;\;\left\{ \begin{array}{l} \frac{{\partial u}}{{\partial t}} + \frac{1}{{{V_f}}}\left( {u{A_x}\frac{{\partial u}}{{\partial x}} + v{A_y}\frac{{\partial u}}{{\partial y}} + w{A_z}\frac{{\partial u}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {g_x} + {f_x}\\ \frac{{\partial v}}{{\partial t}} + \frac{1}{{{V_f}}}\left( {u{A_x}\frac{{\partial v}}{{\partial x}} + v{A_y}\frac{{\partial v}}{{\partial y}} + w{A_z}\frac{{\partial v}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {g_y} + {f_y}\\ \frac{{\partial w}}{{\partial t}} + \frac{1}{{{V_f}}}\left( {u{A_x}\frac{{\partial w}}{{\partial x}} + v{A_y}\frac{{\partial w}}{{\partial y}} + w{A_z}\frac{{\partial w}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + {g_z} + {f_z} \end{array} \right. $ | (2) |
| $ 紊动能 k方程:\;\;\frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (\rho k{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[ {{\sigma _k}\left( {\mu + {\mu _{\rm{t}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_k} - \rho \varepsilon $ | (3) |
| $ 紊动能耗散率\varepsilon 方程:\frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (\rho \varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_i}}}\left[ {{\sigma _\varepsilon }\left( {\mu + {\mu _{\rm{t}}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_i}}}} \right] + {C_{\varepsilon 1}}\frac{\varepsilon }{k}{G_k} - {C_{\varepsilon 2}}\rho \frac{{{\varepsilon ^2}}}{k} $ | (4) |
式中:u,v,w分别为x,y,z方向上的流速分量(m/s); Ax,Ay,Az分别为x,y,z方向上可流动的面积分数(m2); gx,gy,gz分别为x,y,z方向的重力加速度(m/s2); fx,fy,fz分别为x,y,z方向上的黏滞力((kg·m)/s2); Vf为可流动的体积分数(m3); ρ为液体密度,本文研究对象为水,取值为1 000 kg/m3; p为压力(Pa); k为紊动能(m2/s2); ε为紊动耗散率((kg·m2)/s2); σk,σε分别为紊动能k和耗散率ε相对应的Prandtl数,均为1.39;μ,μt分别为液体的动力黏滞系数和紊动黏滞系数(N·s/m2); Gk为紊动能k的产生项,不可压缩流体Gk=0;Cε1,Cε2为经验常数,分别为1.42和1.68;i,j=1,2,3。
2.2 自由表面的处理采用VOF法可以捕捉自由液面运动,提高自由液面波动模拟精度,计算结果准确[9-12]。VOF法通过确定流体和空气所占的体积之比来获取自由液面的位置信息,F=1表示单元内空间被流体占满,F=0表示单元内空间被空气占满,0<F<1表示自由液面。
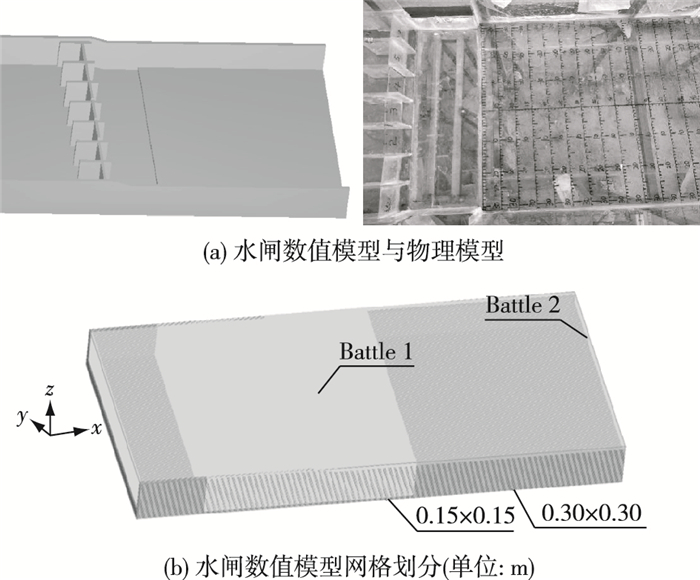
2.3 模型建立及网格划分图 2为模型及网格划分。计算区域起点选在坝轴线上游50 m,后接闸室段、消力池段及下游冲刷段,终点选在河道中心线下游89 m。每个网格单元尺寸为0.30 m×0.30 m,闸门附近及下游流态复杂的地方采用内嵌式网格,网格单元尺寸为0.15 m×0.15 m。以河道中心线方向为y方向,垂直河道中心线下游方向为x轴正方向,垂直x,y方向向上为z轴正方向。原点位置选在河道中心线上游起点处,以消力池底部高程作为z方向零点。
|
图 2 模型及网格划分 Figure 2 Schematic diagram of model and grid division |
试验装置采用有机玻璃制成,其糙率取值范围为0.008~0.009。根据重力相似准则,数学模型中的糙率取值范围是0.017 2~0.019 4,经反复调参运行后,取糙率n=0.017 5。上下游边界采用由水流高度控制的压力边界,上游水深设置为7 m,下游水深单孔与连续三孔开启时分别为1和2 m; 渠道两侧及底部选择固壁边界; 顶部空气入口设置成压力边界,F设置为0,代表上边界全部为空气。以上下游控制水位作为不同工况下的初始水位,流体选用温度为20 ℃的水。
3 结果与分析 3.1 水流流态试验设计中提出的几种工况下跃后水深的计算值与试验值见表 1。可见计算结果误差范围为0.84%~4.75%,平均误差为2.48%,验证了数学模型计算的可靠性。
| 表 1 不同工况下跃后水深数值模拟与试验值对比 Table 1 Comparison between simulated values and testing values of water depth under different working conditions |
图 3为多孔水闸单孔和连续3孔分别开启时在设置导流墙前后数模与物模试验的水流流态对比。计算结果显示,上游闸前段水流平稳,未加导流墙时下泄水流集中,由于主流受到两侧静水挤压,单宽流量q增大,消力池两侧产生回流,回流区离心力的作用进一步加剧了对主流的挤压,相应的临界水深进一步增大。由于多孔水闸少数孔开启泄流量较小,主流在海漫上扩散后下游水深进一步降低,消力池尾部壅高的水位出池与下游小水深相连发生水跃,继而在海漫上出现二次水跃现象。加导流墙后,单孔闸门开启时主流在导流墙后仍受到两侧静水挤压,水跃发生的位置退后导致主流在消力池内消能不充分; 3孔闸门开启时导流墙的存在有效缓解了两侧静水及回流对主流的挤压作用,水跃宽度增加,这与物理试验结果一致。

|
图 3 不同工况下数值模拟与物理试验水流流态对比 Figure 3 Comparison between flow regime by numerical simulation and physical tests under different working conditions |
表 2给出了不同导流墙长度时水流流态特征。结合图 3分析,单孔开启时出闸主流在导流墙段内没有受到两侧静水区的挤压,但在出导流墙后两侧静水区仍然对主流产生挤压作用,布置导流墙并没有有效降低跃后水深,且一次水跃发生的位置距离闸门的距离增加。出池处主流宽度随着导流墙长度的增加而减小,主流扩散不充分,出池后又受到下游尾水的挤压进而二次水跃宽度越来越窄。与无导流墙时情况相比,在导流墙长度为消力池长度的50%和60%时,跃后水深分别增加2.36%和4.39%。在导流墙长度为消力池长度的75%和100%时,跃后水深分别降低8.78%和0.33%。主要原因是当导流墙长度较长时,大部分水跃发生在消力池后的海漫上,渠底高程增加。在4种不同长度的情况下,二次水跃距消力池尾部距离分别增加了3.89%, 11.69%, 1.29%和14.29%。二次水跃过后,水流又呈羊角状向两边扩散。
| 表 2 单孔和3孔闸门开启时不同导流墙长度下水流流态特征 Table 2 Flow regime characteristics of different training wall lengths during opening of a single gate and three gates |
3孔开启时布置导流墙可以有效避免主流被压缩,水跃宽度较未加导流墙时增加。与未加导流墙时情况相比,加4种不同长度导流墙时跃后水深分别降低了4.16%,1.66%,1.94%和2.22%,二次水跃与消力池尾部距离分别缩短了17.14%,14.29%,2.86%和1.43%。加0.50Ls导流墙时,导流墙的存在对主流在出池位置的扩散影响较小,二次水跃长度明显缩短。随导流墙长度的增加,导流墙对主流扩散的抑制作用加强,出池时主流宽度束窄,二次水跃宽度也随之变窄直至为零,导致二次水跃跃后水深增加,海漫上水深分布不均匀。两种开启方式下随导流墙长度增加回流现象减弱,导流墙为Ls时回流现象基本消失。
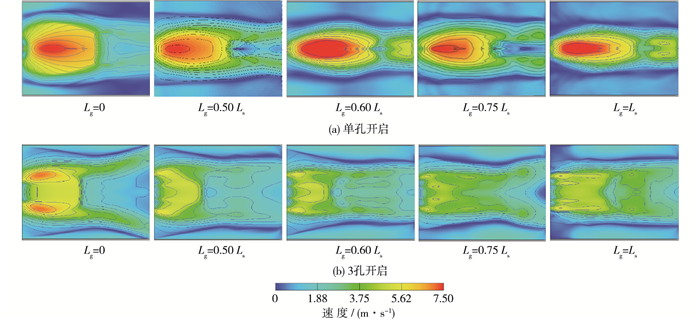
3.2 海漫区近底流速分布河床发生冲刷的原因是河道中近底流速大于河床的不冲流速。近底水体的流速测量十分困难,也是底流消能工的一项重要水力学指标。图 4为在不同开启方式下消力池底部以上1.2 m水平断面处海漫区的近底流速分布情况,图 5为距池尾下游60 m即x=130 m处横断面近底流速分布。
|
图 4 z=1.2 m处不同导流墙长度下速度分布云图 Figure 4 Velocity distribution diagram of different guide wall lengths at z=1.2 m |
单孔开启时泄流量较小,主流扩散造成下游尾水降低导致水跃后半部分与下游衔接恶劣,流速分布不均匀。布置导流墙后,由于水流扩散受到影响,消力池后流速进一步增大。且导流墙长度的增加加剧了导流墙对主流扩散的抑制作用,导致跃后急流部分流速增大,流速集中区域加长。由图 5(a)可知,加导流墙后海漫末端的近底流速随导流墙长度增加而增大且由于扩散不充分流速分布也愈加集中。

|
图 5 x=130 m处横断面不同导流墙长度下近底流速分布 Figure 5 Near-bottom velocity distribution at x=130 m cross section with different training wall lengths |
3孔开启时,池中主流受到两侧静水区及回流挤压、导流墙对前部分主流受挤压及后部分主流扩散的抑制3种作用共同影响,当Lg=0.50Ls时,二次水跃前流速集中位置较短,海漫末端流速分布比较均匀,导流墙对主流扩散的抑制作用不明显。Lg继续增加,主流束窄愈加严重,两侧空间对主流扩散基本不起作用。由图 5(b)可以看出,当导流墙长度Lg=0.50Ls时,海漫末端流速分布最均匀且最大流速Vmax最小。
4 结语(1) 多孔水闸单孔开启时会产生二次水跃问题,导流墙使主流在消力池内不能充分扩散,跃后水深增加,二次水跃变长。
(2) 多孔水闸连续3孔开启时, 多孔隔3孔布置1道长度Lg=0.50Ls的导流墙,减弱了两侧静水及回流在消力池前部对主流的挤压且对水跃后半部分扩散影响最小,有效降低了跃后水深且二次水跃发生的位置提前,海漫上流速分布最均匀。
(3) 由于时间关系,只分析研究了多孔闸门单孔和连续3孔开启时消力池内加导流墙闸后水流流态分布规律,对于闸门其他开启情况下导流墙对闸后三元水跃的影响有待进一步试验及数值模拟分析。
| [1] |
SL 265—2016水闸设计规范[S]. (SL 265—2016 Design specification for sluice[S]. (in Chinese))
|
| [2] |
王才欢, 肖兴斌. 底流消能设计研究与应用现状述评[J]. 四川水力发电, 2000, 19(1): 79-81, 85. ( WANG Caihuan, XIAO Xingbin. Application and study on energy dissipator for bottom current at present[J]. Sichuan Water Power, 2000, 19(1): 79-81, 85. DOI:10.3969/j.issn.1001-2184.2000.01.032 (in Chinese)) |
| [3] |
冬俊瑞, 李永祥, 李玉柱. 中小型水工建筑物底流水跃消能技术新进展[J]. 海河水利, 1996(6): 4-8. ( DONG Junrui, LI Yongxiang, LI Yuzhu. New development of energy dissipation technology for bottom water flow of small and medium sized hydraulic structures[J]. Haihe Water Resources, 1996(6): 4-8. (in Chinese)) |
| [4] |
韩伟濛, 吴鑫淼, 苗臣伟. 多孔水闸少数孔开启条件下主流扩散研究[J]. 河北农业大学学报, 2017, 40(3): 114-118, 123. ( HAN Weimeng, WU Xinmiao, MIAO Chenwei. Study on mainstream diffusion under part opening of multiple-outlet sluice[J]. Journal of Agricultural University of Hebei, 2017, 40(3): 114-118, 123. (in Chinese)) |
| [5] |
RAJARATNAM N, SUBRAMANYA K. Hydraulic jumps below abrupt symmetrical expansions[J]. Journal of the Hydraulics Division, 1968, 94(2): 481-504. |
| [6] |
陈鸿丽. 三峡工程左导墙设计研究[J]. 水利水电快报, 2000, 21(19): 21-25. ( CHEN Hongli. Design of the left guiding wall of the Three Gorges Project[J]. Express Water Resources & Hydropower Information, 2000, 21(19): 21-25. (in Chinese)) |
| [7] |
李华, 马媛. 平原水闸消力池型式的比较[J]. 山东水利科技, 1986(3): 31-35. ( LI Hua, MA Yuan. Comparison of stilling basin type of plain sluice[J]. Water Resources Science and Technology of Shandong, 1986(3): 31-35. (in Chinese)) |
| [8] |
龚彦奎, 蔡报智. 平原多孔水闸少数孔开启的消能问题[J]. 海河水利, 1992(6): 17-21. ( GONG Yankui, CAI Baozhi. Energy dissipation of opening partly in plain multiple-outlet sluice[J]. Haihe Water Resources, 1992(6): 17-21. (in Chinese)) |
| [9] |
葛旭峰, 王长新, 李琳. 陡坡后消力池内水跃的数值模拟[J]. 水利水运工程学报, 2012(3): 70-74. ( GE Xufeng, WANG Changxin, LI Lin. Turbulence model of hydraulic jump in a post-steep plunge pool[J]. Hydro-Science and Engineering, 2012(3): 70-74. DOI:10.3969/j.issn.1009-640X.2012.03.012 (in Chinese)) |
| [10] |
BAYON A, VALERO D, GARCÍA-BARTUAL R, et al. Performance assessment of OpenFOAM and FLOW-3D in the numerical modeling of a low Reynolds number hydraulic jump[J]. Environmental Modelling & Software, 2016, 80: 322-335. |
| [11] |
JING S G, GAO X P, JIA L F, et al. Three-dimensional numerical simulation of the hydraulic characteristics of spillway in Gushitan reservoir[J]. Applied Mechanics and Materials, 2013, 256. |
| [12] |
李玲, 陈永灿, 李永红. 三维VOF模型及其在溢洪道水流计算中的应用[J]. 水力发电学报, 2007, 26(2): 83-87. ( LI Ling, CHEN Yongcan, LI Yonghong. Three-dimensional VOF model and its application to the water flow calculation in the spillway[J]. Journal of Hydroelectric Engineering, 2007, 26(2): 83-87. DOI:10.3969/j.issn.1003-1243.2007.02.017 (in Chinese)) |
 2018
2018 
