2. 南京水利科学研究院,江苏 南京 210029
省水船闸是在船闸的一侧或两侧布置若干级蓄水池以达到省水和合理利用水资源的目的[1]。在水资源相对匮乏的河流特别是运河上建船闸,节省船闸耗水是设计的重要目标[2]。阀门水力学问题一直是高水头船闸设计的关键技术难点,省水船闸不仅可以节省水量,还可以降低高水头船闸阀门工作水头,简化阀门水力学问题并改善闸室及下游引航道水流条件,有利于减轻阀门段廊道空蚀空化及阀门振动。高水头船闸采用省水布置将是我国未来船闸设计的发展方向[3-7]。
双线互输水船闸是一种水力特殊的省水船闸,即两线船闸互为省水池。其输水过程主要分为两部分:一是互输水过程,打开连通阀门使泄水闸室的水注入到充水闸室; 二是单线输水过程,在两个闸室内水面齐平后,泄水闸室泄水到下游,充水闸室由上游取水灌满。这种布置的船闸虽然不能降低联通阀门的工作水头,但可以降低高水头船闸阀门在高水头条件下工作的历时,有利于预防阀门空化[8]。但是,双线互输水船闸会延长过闸历时,降低船闸通过能力,故一般在两闸室有一定剩余水头时,关闭联通阀门的同时开启充、泄水阀门以缩短输水时间,提高船闸的通过能力[1]。
目前,《船闸输水系统设计规范》[9]中还没有省水船闸的剩余水头设计和选取相关的内容,国内外尚无与之相关的专门研究。由于输水时间与省水率为一对矛盾,单纯考虑输水时间或省水量都无法获得最优的剩余水头。可以由剩余水头与输水时间和省水率的关系建立相关经济学模型,从而在船闸高效安全运行的前提下,使其经济效益最大化。本文以长洲三、四线船闸为例,重点研究互输水船闸输水系统水力学,揭示剩余水头与输水时间的关系,为剩余水头的选取提供参考。
1 工程概况长洲三、四线船闸按最大通过船舶为3 000 t级设计,为I级船闸,采用并列布置方案,是目前国内乃至世界范围内规模最大的单级船闸[10-11]。船闸输水系统布置见图 1。船闸设计有效尺度(闸室长×宽×门槛水深)为340 m×34 m×5.8 m。船闸运行设计水头为18.2 m(上游正常蓄水位为20.6 m,下游最低通航水位2.4 m),设计输水时间为10~12 min。阀门段廊道尺寸为4.6 m×6.0 m(宽×高),阀门段廊道断面面积为55.2 m2。连通廊道阀门段面积亦为55.2 m2,与输水阀门段廊道一致。为改善长洲三、四线船闸引航道水流条件及输水系统的工作特性,同时为节省船闸耗水量从而提高发电效益,考虑到双线船闸布置的特点,将两线船闸闸底出水段廊道通过两个连通廊道相连,并设置阀门以控制两线船闸间的输水。船闸运行方式为单线运行模式及双线互输水运行模式,即:(1)单线船闸运行时,采用tv=5 min匀速开启充、泄水阀门方式; (2)双线相互输水运行时,采用tv1=5 min,tv2=3 min,tv3=5 min,d=4~6 m的运行方式,即先以tv2=3 min匀速开启联通阀门,直至剩余水头达到4~6 m时,以tv1=5 min匀速开启充、泄水阀门的同时以tv3=5 min匀速关闭联通阀门。输水系统流量系数见表 1。
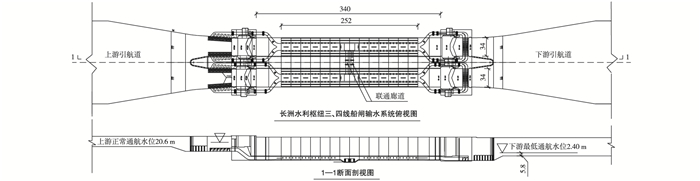
|
图 1 长洲水利枢纽三、四线船闸输水系统布置(单位:m) Figure 1 Layout of filling and emptying system of Changzhou navigation locks No.3 & 4 (unit: m) |
| 表 1 长洲三、四线船闸输水阀门流量系数 Table 1 Water delivery valve discharge coefficients of Changzhou locks No.3 & 4 |
输水涵洞示意见图 2,由伯努利能量方程建立非恒定流能量方程。需要注意的是,由于输水末期闸室超灌、超泄,故水头损失项宜取与流速相同的符号,即水头损失项中的流速需加绝对值[12]。
| $ \frac{{{L_{{\rm{np}}}}}}{g}\frac{{{\rm{d}}v}}{{{\rm{d}}t}} + \xi \frac{{v|v|}}{{2g}} - h = 0 $ | (1) |
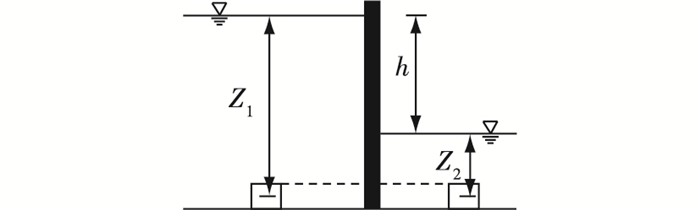
|
图 2 船闸输水示意 Figure 2 Lock's water conveyance culvert |
式中:h为水位差(m); g=9.81 m/s2; Lnp廊道换算长度(m); ξ为输水系统阻力系数,
水体连续性方程:
| $ {A_1}{\rm{d}}h/{\rm{d}}t = - N{A_{\rm{c}}}v $ | (2) |
式中:A1为闸室水域面积(m2); N为输水廊道个数; Ac为输水廊道控制断面面积(m2); dh为闸室水位增量(m),闸室水位下降为正,上升为负; dt为时间增量(s)。
2.2 互输水运行工况控制方程船闸互输水工况的非恒定流能量方程与单充单泄工况运行时相同,但由于相互充、泄过程中,假设两侧闸室面积相同,两闸室水位差变化dh,但只有A1dh/2的水体流经输水廊道控制断面,故其连续性方程为:
| $ {A_1}{\rm{d}}h/(2{\rm{d}}t) = - N{A_{\rm{c}}}v $ | (3) |
为缩短输水时间,两线闸室在达到剩余水头的时候,联通阀门以5 min匀速关闭的同时,充、泄水阀门以5 min匀速开启。如图 3所示,各闸室的能量方程和连续性方程如下:
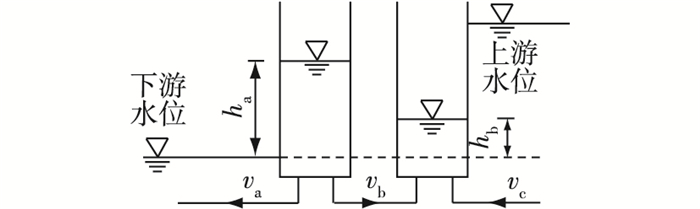
|
图 3 船闸互输水示意 Figure 3 Lock's mutual water conveyance culvert |
非恒定流能量方程:
| $ \left\{ \begin{array}{l} {h_{\rm{a}}} = {\xi _1}\frac{{{v_{\rm{a}}}|{v_{\rm{a}}}|}}{{2g}} + \frac{{{L_{{\rm{np1}}}}}}{g}\frac{{{\rm{d}}{v_{\rm{a}}}}}{{{\rm{d}}t}}\\ {h_{\rm{a}}} = {h_{\rm{b}}} + {\xi _2}\frac{{{v_{\rm{b}}}|{v_{\rm{b}}}|}}{{2g}} + \frac{{{L_{{\rm{np2}}}}}}{g}\frac{{{\rm{d}}{v_{\rm{b}}}}}{{{\rm{d}}t}}\\ H - {h_{\rm{b}}} = {\xi _3}\frac{{{v_{\rm{c}}}|{v_{\rm{c}}}|}}{{2g}} + \frac{{{L_{{\rm{np3}}}}}}{g}\frac{{{\rm{d}}{v_{\rm{c}}}}}{{{\rm{d}}t}} \end{array} \right. $ | (4) |
连续性方程:
| $ \left\{ \begin{array}{l} {A_1}\frac{{{\rm{d}}{h_{\rm{a}}}}}{{{\rm{d}}t}} = - ({v_{\rm{a}}} + {v_{\rm{b}}})N{A_{\rm{c}}}\\ {A_1}\frac{{{\rm{d}}{h_{\rm{b}}}}}{{{\rm{d}}t}} = - ({v_{\rm{b}}} + {v_{\rm{c}}})N{A_{\rm{c}}} \end{array} \right. $ | (5) |
式中:H为上下游水位差(m); va为泄水廊道控制断面处的平均流速(m/s); vb为联通控制断面处平均流速(m/s); vc为充水廊道控制断面处平均流速(m/s); ξ1为泄水廊道阻力系数; ξ2为联通廊道阻力系数; ξ3为充水廊道阻力系数。
2.3 控制方程离散求解由于控制方程是一阶变系数非齐次非线性常微分方程组,采用有限差分法离散该微分方程,求其数值解。求解基于Wolfram语言的mathematics软件建立计算、迭代程序,其NDSolve函数用迭代法求解,既可处理单个微分方程,又可处理联立微分方程组,以及范围很广的常微分方程以及某些偏微分方程[13]。
2.4 数学模型验证如图 4所示,由原观资料可知,四线单独充水、三线单独泄水(图 4(a)),三、四线互输水(剩余水头d=3.2 m),联通阀门全关后开启充、泄水阀门(图 4(b))。在人字门未打开之前,闸室水位计算值与实测值吻合,打开人字门后,闸室水体与上下游水体联通,超灌、超泄引起的水位波动基本消失。随着时间推移,闸室水位基本趋于上下游水位。故实测值与计算值趋于吻合,可以用数学模型进行计算。
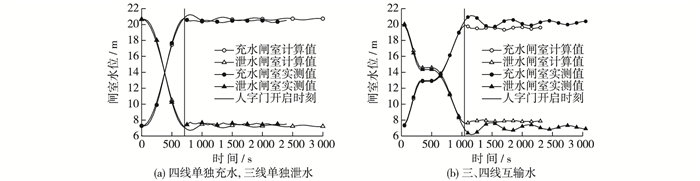
|
图 4 闸室水位过程线 Figure 4 Water level hydrograph in lock chambers |
由船闸水力学[1]可知,省水船闸的省水率
| $ \beta = \nu n/\left( {1 + \nu + \nu n} \right) $ | (6) |
式中:ν=Ωσ/Ωk,Ωσ为闸室水面面积; Ωk为蓄水池水面面积; n为蓄水池级数。
由于双线互输水船闸在达到剩余水头后联通阀门并不是迅速关闭,在关闭联通阀门的同时两闸室还有部分水体交换,故省水率不能简单由此公式计算。但可以从省水率的定义出发即省水率为输入蓄水池的水体体积与闸室水体总体积的比值,双线互输水船闸1次节省的水量即为经过联通阀门的水量,在求解船闸输水方程时可以求得联通廊道控制断面处的平均流速,因此可以将该流速对时间进行积分。由于解析解很难求出,故可对离散的数值解求和,即节省的水量和省水率可由下式计算:
| $ {w_1} = {A_{\rm{c}}}\sum {v_i}\Delta t $ | (7) |
| $ \beta = {w_1}/({\Omega _{\rm{ \mathsf{ σ} }}}H) $ | (8) |
式中:Ac为输水廊道控制断面面积(m2); vi为控制断面各时刻的水流流速(m/s); H为上下游水位差(m)。可以计算得出剩余水头对应的省水率,由此计算得出的省水率与剩余水头的关系见表 2。在此必须指出,在联通阀门关闭的5 min内由于充水闸室水位会高于泄水闸室水位,因此联通廊道的流速会出现负值,即充水闸室倒流泄水闸室,这就是出现随着剩余水头增大,省水率先增后减的原因。
| 表 2 剩余水头与省水率 Table 2 Rates of water saving corresponding to different residual water heads |
根据以上船闸输水系统非恒定流能量方程和连续性方程可以计算出每个剩余水头d对应的闸室水位过程线。现将几个典型剩余水头对应的闸室水位过程线列于图 5,由图可见,随着剩余水头增加,闸室水位过程线下降、上升速度明显加快,船闸输水时间不断减小。
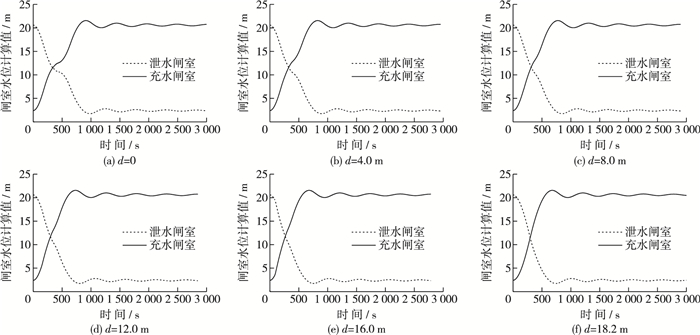
|
图 5 闸室水位过程线 Figure 5 Water level hydrograph in lock chambers |
由于泄水廊道流量系数低于充水廊道流量系数,所以在1次充、泄水过程中,泄水时间要略长于充水时间。故将泄水闸室水位第1次与下游水位(2.4 m)齐平时视作充、泄水完成(人字门开启时刻)。这样由闸室水位过程线可得每个剩余水头对应的输水时间,统计各剩余水头d对应的输水时间如表 3所示。
| 表 3 剩余水头与输水时间 Table 3 Water delivery time corresponding to different residual water heads |
船闸通过能力不仅与灌泄水时间、闸门启闭时间等有关,还与船舶类型、船舶进出闸的速度与数量以及船员的操作熟练程度等有关。因为充、泄水时间与其他时间相对独立,为简化问题,数学模型只考虑充、泄水时间对1次过闸时间的影响。
剩余水头与输水时间和省水率关系见图 6,由以上分析可知,省水率随着剩余水头增大的过程中会在4 m左右出现峰值,这是因为在5 min内关闭联通阀门时由于充水闸室的水位会高于泄水闸室,即会出现倒流现象,最大省水率出现在5 min内关闭连通阀门时两闸室的水位刚好齐平的时候。故从省水率最大的角度出发优化剩余水头,考虑到剩余水头控制精度,剩余水头取4 m为最优。
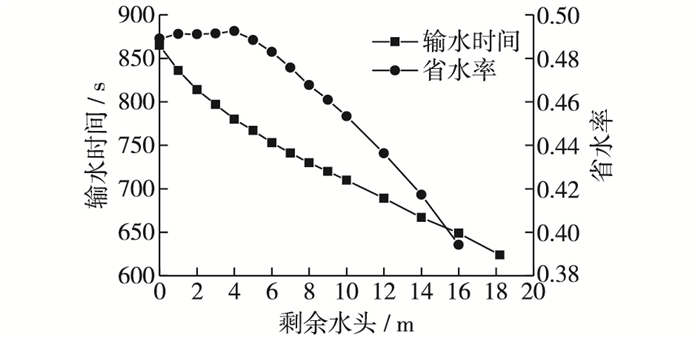
|
图 6 剩余水头与输水时间和省水率 Figure 6 Relationships between water delivery time and water saving rates corresponding to different residual water heads |
由于输水时间与省水率是相互矛盾的体系,即输水时间短则省水率低。若综合考虑船闸通过能力和省水率,如何选取合适的剩余水头,既保证输水时间较短又保证省水率较高是很值得研究的问题。综上研究表明,可以由剩余水头与输水时间和省水率的关系曲线,结合省水率与输水时间在剩余水头选取上的权重,从而建立相关经济学模型,并在船闸高效安全运行前提下,使其经济效益最大化。文中仅提出这种研究思路,具体模型还有待进一步开发研究。
5 结语通过船闸输水系统非恒定流能量方程和连续性方程建立双线互输水船闸的输水数学模型,研究了在不同剩余水头下的船闸输水时间和省水率的关系。由数学模型计算结果可知,省水率在剩余水头约4 m处出现峰值0.50,故从省水角度出发,长洲三、四线船闸的剩余水头d=4 m为最优。牺牲省水率则缩短输水时间提高船闸通过能力,可以由剩余水头与输水时间和省水率的关系建立相关经济学模型,从而使船闸在高效安全运行的前提下,其经济效益最大化。关于省水率与输水时间的经济学模型还有待进一步研究。
| [1] |
Б Д卡洽诺夫斯基. 船闸水力学[M]. 华东水利学院水道及港口教研组, 译. 北京: 水利出版社, 1957. (КAYAHOBCKNH Б Д. Ship lock hydraulics[M]. Translated by Waterway and Harbor Teaching and Research Group of East China Water Conservancy Institute. Beijing: China Hydraulic Press, 1957. (in Chinese))
|
| [2] |
吴澎, 宣国祥. 船闸设计的新进展[J]. 水利水运工程学报, 2009(4): 122-127. ( WU Peng, XUAN Guoxiang. New advances in navigation lock design[J]. Hydro-Science and Engineering, 2009(4): 122-127. DOI:10.3969/j.issn.1009-640X.2009.04.016 (in Chinese)) |
| [3] |
陈明栋. 带调节水池船闸的水力学问题初探[J]. 重庆交通学院学报, 1994, 13(4): 61-67. ( CHEN Mingdong. Preliminary study on hydraulic problem of super high head lock with regulating pond[J]. Journal of Chongqing Jiaotong Institute, 1994, 13(4): 61-67. (in Chinese)) |
| [4] |
刘本芹, 李云, 胡亚安, 等. 高水头大尺度船闸省水布置与水力计算[J]. 水运工程, 2016(12): 42-46. ( LIU Benqin, LI Yun, HU Ya'an, et al. Water-saving layout and hydraulic simulation of high head and large scale ship lock[J]. Port & Waterway Engineering, 2016(12): 42-46. DOI:10.3969/j.issn.1002-4972.2016.12.007 (in Chinese)) |
| [5] |
周玉华, 刘锋. 省水船闸初探[J]. 水运工程, 2006(10): 156-159. ( ZHOU Yuhua, LIU Feng. Preliminary study on water-saving ship lock[J]. Port & Waterway Engineering, 2006(10): 156-159. DOI:10.3969/j.issn.1002-4972.2006.10.028 (in Chinese)) |
| [6] |
王晓青, 刘兆存, 张长腾. 飞来峡双线省水船闸水力学特性试验[J]. 水利水电技术, 2016, 47(5): 53-55. ( WANG Xiaoqing, LIU Zhaocun, ZHANG Changteng. Study on hydraulic characteristics of Feilaixia water-saving double-line ship locks[J]. Water Resources and Hydropower Engineering, 2016, 47(5): 53-55. (in Chinese)) |
| [7] |
陈明栋, 杨斌, 杨忠超, 等. 省水船闸在高坝通航中的应用[J]. 水运工程, 2008(12): 114-118. ( CHEN Mingdong, YANG Bin, YANG Zhongchao, et al. Application of water saving lock to navigation of high dam[J]. Port & Waterway Engineering, 2008(12): 114-118. DOI:10.3969/j.issn.1002-4972.2008.12.025 (in Chinese)) |
| [8] |
李云, 胡亚安, 宣国祥. 通航船闸水力学研究进展[J]. 水动力学研究与进展(A辑), 1999, 14(2): 232-239. ( LI Yun, HU Ya'an, XUAN Guoxiang. Advances in study on hydraulics of navigation lock[J]. Journal of Hydrodynamics(SerA), 1999, 14(2): 232-239. (in Chinese)) |
| [9] |
JTJ306—2001船闸输水系统设计规范[S]. (JTJ306—2001 Design specification for ship locks water conveyance system[S]. (in Chinese))
|
| [10] |
吴澎, 曹凤帅. 西江长洲水利枢纽3号和4号船闸总体设计[J]. 港工技术, 2014, 51(5): 4-9. ( WU Peng, CAO Fengshuai. Overall design of lock No.3 & 4 for Changzhou Hydro-junction on Xijiang River[J]. Port Engineering Technology, 2014, 51(5): 4-9. DOI:10.3969/j.issn.1004-9592.2014.05.002 (in Chinese)) |
| [11] |
张珊, 吴澎. 长洲水利枢纽3-4号船闸平面布置研究[J]. 水利水运工程学报, 2012(4): 1-5. ( ZHANG Shan, WU Peng. Research on layout for locks No.3 and No.4 of Changzhou water control project on Xijiang River[J]. Hydro-Science and Engineering, 2012(4): 1-5. DOI:10.3969/j.issn.1009-640X.2012.04.001 (in Chinese)) |
| [12] |
孟祥玮, 周华兴, 高学平. 船闸输水基本方程的应用[J]. 水利水电技术, 2008, 39(10): 45-47. ( MENG Xiangwei, ZHOU Huaxing, GAO Xueping. Application of basic equation of water filling-emptying for ship lock[J]. Water Researches and Hydropower Engineering, 2008, 39(10): 45-47. DOI:10.3969/j.issn.1000-0860.2008.10.012 (in Chinese)) |
| [13] |
章美月. Mathematica数学软件与数学实验[M]. 徐州: 中国矿业大学出版社, 2013. ( ZHANG Meiyue. Mathematica mathematical software and mathematical experiments[M]. Xuzhou: China University of Mining and Technology Press, 2013. (in Chinese))
|
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2018
2018 
