2. 三峡大学土木与建筑学院,湖北 宜昌 443002
混凝土的动力特性影响因素较多,对其进行的研究和认识也趋于全面和成熟[1-3]。混凝土受剪状态下的力学特性,国内外学者也进行了诸多试验研究。张力伟等[4]利用声发射装置对酸腐蚀后的混凝土进行抗剪加载试验全过程信号采集;Amin等[5]对矩形简支梁进行了钢纤维配筋率的试验研究,分析了完整的材料表征,量化后裂解行为的钢纤维混凝土;Jacek等[6-7]对再生骨料混凝土与天然骨料混凝土界面的抗剪强度、轻骨料混凝土梁抗剪承载力进行了试验研究;余茂宏等提出了一种适用于演示材料简单理论,即双剪强度理论的双参数准则[8]。
在强度准则方面,人们也进行了大量理论研究和试验验证[9],推导过程主要有3类:①基于经典强度理论或在其基础上的改进,主要有Mohr-Coulomb准则、Mises准则、Tresca准则等;②以大量试验数据为基础的经验公式,主要有Reimann准则、Willam-Warnke准则、过-王准则等[8];③基于包络面的几何形状特征的数学推导公式,主要有Ottosen准则、Podgorski准则[10]等。
综上可知,混凝土抗剪力学性能及剪切破坏准则的研究大多集中于静态纯剪状态,对于压剪共同作用下混凝土的率效应试验研究还很少。为此本文开展了不同法向应力作用下混凝土受不同加载速率的剪切试验,分析力学性能,并基于Bresler-Pister准则,提出一种可供参考的动态压剪强度准则。
1 试验设备与方法 1.1 试验设备采用三峡大学与长春朝阳试验仪器有限公司联合生产的10 MN大型多功能液压伺服静动力三轴仪,主要由液压油泵、EDC控制器、软件控制系统和加载框架构成,可通过荷载、位移和变形加载方式在3个相互垂直的方向分别加载,所提供竖向最大静、动力荷载值分别为10和5 MN。同时,最小采样间隔为0.000 1 s。
采用剪切盒进行试验。剪切盒由上下两部分组成,外框架由4根钢柱固定,能保持整体稳定。受横向剪切荷载作用时,下半部分通过底部螺栓与外框架连接并保持不动,上半部分通过滑槽和相对外框架做滑移运动。
1.2 试件制备试验所用水泥为P·O 42.5普通硅酸盐水泥;拌合水为饮用自来水;粗骨料为粒径5~40 mm的连续级配碎石;细骨料为连续级配天然河砂,经筛分后实测细度模数为2.3,属于中砂。混凝土材料组成为:水175.0 kg/m3,水泥291.0 kg/m3,细骨料676.9 kg/m3,粗骨料1 257.1 kg/m3。
混凝土试件为边长300 mm的立方体,成型方式为钢模浇筑。为了搅拌均匀,采取先干拌后湿拌的方法。振捣完成后,将表面磨平处理,室温下放置24 h后拆模,拆模后将混凝土放入标准养护室养护,保证相对湿度为95%以上,温度为(20±2)℃,28 d后将混凝土试件移至室外自然养护。
1.3 试验加载过程(1) 预加载。为使传力柱、剪切盒与试件紧密接触,尽量减少三者之间的间隙,在正式加载前先进行预加载。试件安装到剪切盒后,推送至设备中心,分别向竖向和水平向施加10 kN的力。
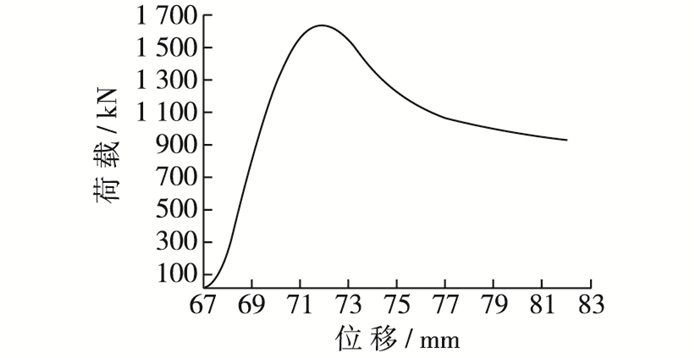
(2) 正式加载。采用荷载控制方法,对试件分别施加10,180,360,540,720和900 kN的轴向恒定荷载,保持恒定。然后按变形控制方法,在水平向按不同加载速率加载,直至得出包含下降段在内的完整剪切力-位移曲线,如图 1所示。
|
图 1 实测荷载-位移全曲线 Figure 1 Measured load-displacement curve |
(3) 卸载及后续处理。得到完整的试验曲线后,停止加载,开始卸载。卸载完成后,清理残渣仪器归位。
2 剪切强度分析 2.1 法向压力对剪切强度的影响在试验基础上,将法向力和水平剪力按式(1)和式(2)转化为试件的法向应力和剪应力。
| $ {\sigma _i} = P/A $ | (1) |
| $ {\tau _i} = Q/A $ | (2) |
式中:σi为法向应力;τi为剪应力;P为总法向力;Q为剪切力;A为剪切面面积。
将试件的法向力按式(1)计算得到法向应力分别为0,2,4,6,8和10 MPa, 在不同法向应力和加载速率下获得的最大水平力按式(2)计算得到剪应力。不同法向应力下的剪应力如表 1所示。
| 表 1 混凝土剪切强度 Table 1 Shear strength of concrete |
在相同加载速率条件下,混凝土法向应力和剪应力的关系如图 2所示。由表 1及图 2可见,混凝土在压剪状态下的剪切强度随法向应力的增大而增大,且不同加载速率下的法向应力对剪切强度的影响趋势基本一致。在一定的法向应力范围内,剪切强度增幅近似呈线性,当超过一定法向应力后,增幅开始变小。混凝土在法向压应力作用下,压应力增大了断裂面之间的摩擦力,降低其内部裂纹的发展速度,从而提高了抗剪强度;法向压应力越大摩擦作用就越强,抗剪强度也越高。文献[11]中提到,在压剪应力状态下,混凝土抗剪强度随着压应力的增大逐渐增大到一最大值,此后由于混凝土内部裂纹的发展,抗剪强度随压应力增大而减小,故剪切强度随着法向压力增大而增大的趋势逐渐变缓。由于混凝土受到法向压力的作用,其内部受力状态从弹性阶段到弹塑性阶段的过程中,内部裂纹逐渐发展,使得法向压力对增大剪断面的摩擦作用减弱,故剪切强度增幅减弱。

|
图 2 剪切强度与法向压力的关系 Figure 2 Relationship curves between shear strength and normal pressure |
结合图 3及表 1可知,随着加载速率的增加,混凝土剪切强度有所提高,但其最大增幅只有10.94%,法向压力对抗剪强度增加作用显著,最小为49.16%,最大可达244.3%。在混凝土动态压剪作用下,混凝土剪切强度的增加主要通过法向压力的增大而增大,加载速率对剪切强度的影响并不明显。

|
图 3 剪切强度增幅与加载速率的关系 Figure 3 Relationship curves between shear strength increment and loading rate |
由图 3还可以看出,随着法向压力增大,剪切强度随加载速率的增幅量也随之增大。这说明随着法向压力的持续增大,混凝土不仅表现为抗剪强度增大,其速率效应也随之增强。
2.3 摩擦系数和黏聚力当法向压力小于8 MPa时,混凝土压剪强度近似服从莫尔-库仑准则[12-14]。根据《水工混凝土试验规程》中的规定,将法向压力8 MPa以下的压剪强度按式(3)进行回归分析,可得到不同加载速率下剪切强度与法向压力之间的关系。
| $ {\tau _{{\rm{pk}}}} = \sigma f' + c' $ | (3) |
式中:τpk为剪切强度; σ为法向压力;f '为摩擦系数;c'为黏聚力。拟合参数见表 2。
| 表 2 摩擦系数和黏聚力的拟合 Table 2 Fitting parameter of friction coefficients and cohesive force |
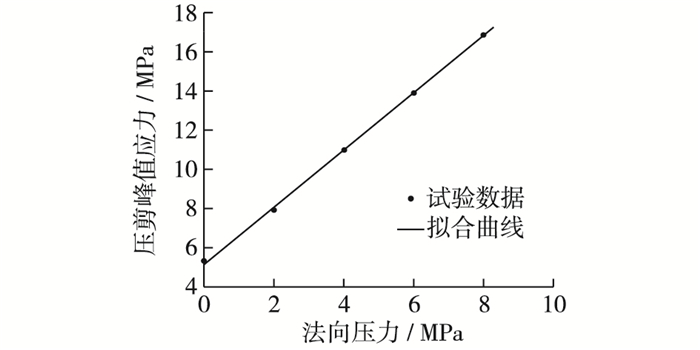
由表 2可知拟合系数均高于0.99,拟合效果很好。图 4给出了加载速率为1.80 mm/min时剪应力和法向压力的拟合。可见,法向压力不大于8 MPa时,混凝土抗剪强度随法向压力的增大基本呈线性增长关系。
|
图 4 剪应力与法向压力的拟合(1.80 mm/min) Figure 4 Fitting curves of shear stress and normal pressure |
Bresler和Pister基于八面体强度理论提出了一种强度准则[8],其原始表达式如式(4)所示。
| $ \frac{{{\tau _{{\rm{oct}}}}}}{{{f_{\rm{c}}}}} = a - b\frac{{{\sigma _{{\rm{oct}}}}}}{{{f_{\rm{c}}}}} + c\left( {\frac{{\sigma _{{\rm{oct}}}^2}}{{{f_{\rm{c}}}}}} \right) $ | (4) |
| $ {\tau _{{\rm{oct}}}} = \sqrt {{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _1} - {\sigma _3})}^2}} /3 $ | (5) |
| $ {\sigma _{{\rm{oct}}}} = ({\sigma _1} + {\sigma _2} + {\sigma _3})/3 $ | (6) |
式中:σoct和τoct为八面体空间下的应力,参照式(5)和(6),将其转换为主应力空间下的强度准则。转换后的强度准则形式为式(7):
| $ \begin{array}{l} \sqrt {{{({\sigma _1} - {\sigma _2})}^2} + {{({\sigma _2} - {\sigma _3})}^2} + {{({\sigma _1} - {\sigma _3})}^2}} /(3{f_{\rm{c}}}) = a - b\\ ({\sigma _1} + {\sigma _2} + {\sigma _3})/(3{f_{\rm{c}}}) + c{\left( {({\sigma _1} + {\sigma _2} + {\sigma _3})/(3{f_{\rm{c}}})} \right)^2} \end{array} $ | (7) |
本试验是混凝土平面压剪应力状态,σ2为0。将压剪平面应力状态与拉压平面应力状态进行转化可得:
| $ {\sigma _1} = \sigma /2 + \sqrt {{\sigma ^2} + 4{\tau ^2}} /2 $ | (8) |
| $ {\sigma _3} = \sigma /2 + \sqrt {{\sigma ^2} + 4{\tau ^2}} /2 $ | (9) |
式中:σ为法向压力;τ为混凝土压剪强度。
将式(8)和(9)代入式(7),可得式(10),即为混凝土压剪静态强度准则表达式,但未考虑率效应。
| $ \sqrt {2{\sigma ^2} + 6{\tau ^2}} /(3{f_{\rm{c}}}) = a - b\sigma /(3{f_{\rm{c}}}) + c{\sigma ^2}/(9f_{\rm{c}}^2) $ | (10) |
假定混凝土在动态荷载下的单轴抗压强度为fcd,动态单轴抗剪强度为fτd,在法向压力为σ=αfcd时的动态压剪强度为fατd。将(fcd,0)和(0,fτd)代入式(10),即可得到关于参数a,b, c的三元二次方程如下:
| $ \left\{ \begin{array}{l} \sqrt 2 /3 = a - b/3 + c/9\\ \sqrt 6 {f_{\tau {\rm{d}}}}/(3{f_{{\rm{cd}}}}) = a \end{array} \right. $ | (11) |
式(11)有3个参数,但只有2个方程,因此还缺少1个方程。由前文可以看出,当法向压力小于8 MPa时,压剪强度随法向压力近似呈线性增长,式(3)适用于不同的加载速率,故可将此式加以推广。
| $ {f_{\alpha \tau {\rm{d}}}} = - f_{\rm{d}}'\sigma + c{'_{\rm{d}}} $ | (12) |
式中:fατd是法向压力为αfcd时混凝土的动态压剪强度;f'd和c'd为动态加载速率下的摩擦系数和黏聚力。混凝土黏聚力等于其纯剪强度,即c'd=fτd。式(12)可转化为
| $ {f_{\alpha \tau {\rm{d}}}} = - \alpha {f_{{\rm{cd}}}}f{'_{\rm{d}}} + {f_{\tau {\rm{d}}}} $ | (13) |
由表 2可知,当法向压力小于8 MPa时,σ和fατd近似呈线性分布。fατd可由式(12)求出。为方便计算,取α=0.1,将(f0.1τd, 0.1fcd)代入式(11),得到式(14)。
| $ \sqrt {\frac{{0.02}}{9} + \frac{{2f_{0.1\tau {\rm{d}}}^2}}{{3f_{{\rm{cd}}}^2}}} = a - \frac{b}{{30}} + \frac{c}{{900}} $ | (14) |
将式(13)代入式(14),可得a, b, c间的第3个独立方程式,并与式(11)联立可得:
| $ \left\{ \begin{array}{l} \sqrt 2 /3 = a - b/3 + c/9\\ \sqrt 6 {f_{\tau {\rm{d}}}}/(3{f_{{\rm{cd}}}}{\rm{)}} = a\\ \sqrt {0.02/9 + 2{{({f_{\tau {\rm{d}}}} - 0.1f{'_{\rm{d}}}{f_{{\rm{cd}}}})}^2}/(3f_{{\rm{cd}}}^2)} = a - b/30 + c/900 \end{array} \right. $ | (15) |
式(15)中,根据试验数据确定混凝土的单轴抗压动态强度准则、纯剪动态强度准则以及动态摩擦系数的率效应表达式,即可求出任一加载速率下的a,b,c。
单轴抗压动态强度准则选用欧洲规范[15]:
| $ {f_{{\rm{cd}}}}/{f_{\rm{c}}} = \left\{ {\begin{array}{*{20}{c}} {{{\left( {\varepsilon {'_{{\rm{cd}}}}/\varepsilon {'_{{\rm{c}}0}}} \right)}^{1.026m}}, }&{\varepsilon {'_{{\rm{cd}}}} \le 30/{\rm{s}}}\\ {\gamma \varepsilon{'} _{{\rm{cd}}}^{1/3}, }&{\varepsilon {'_{{\rm{cd}}}} > 30/{\rm{s}}} \end{array}} \right. $ | (16) |
式中:fcd为动态抗压强度;fc为静态抗压强度;m为材料参数;ε'cd为动态加载速率;ε'c0为静态加载速率;γ为控制参数。
纯剪强度准则采用:
| $ {f_{\tau {\rm{d}}}}/{f_\tau } = {\left( {s{'_{\rm{d}}}/s{'_0}} \right)^n} $ | (17) |
式中:fτd为动态抗剪强度;fτ为静态抗剪强度;s'd为动态加载速率;s'0为静态加载速率(取0.18 mm/min);n为材料参数。
混凝土剪切面摩擦系数的率效应采用:
| $ f{'_{\rm{d}}}/f' = {\left( {s{'_{\rm{d}}}/s{'_0}} \right)^k} $ | (18) |
式中:f'd为动态加载速率下的摩擦系数;f'为静态加载速率下的摩擦系数;k为材料参数。
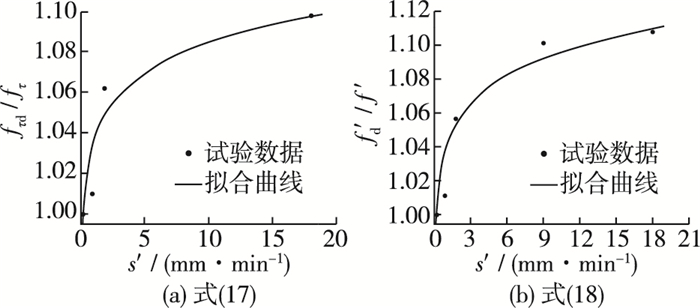
为了进一步确定式(17)和(18)的可靠性,将试验数据分别采用式(17)和(18)拟合得图 5(a)和(b)。由图 5可知,拟合效果良好,拟合相关系数分别为R2=0.923 2,R2=0.925 1。
|
图 5 式(17)和(18)的验证 Figure 5 Curves fitted by equations (17) and (18) |
根据式(10),可将其改写为动态加载速率下的表达式(19)。
| $ \begin{array}{l} \frac{{\sqrt {2{\sigma ^2} + 6{\tau ^2}} }}{{3{f_{\rm{c}}}{{(s{'_{\rm{d}}}/s{'_0})}^{1.026m}}}} = a - b\frac{\sigma }{{3{f_{\rm{c}}}{{(s{'_{\rm{d}}}/s{'_0})}^{1.026m}}}}\\ + c\frac{{{\sigma ^2}}}{{9{{({f_{\rm{c}}}{{(s{'_{\rm{d}}}/s{'_0})}^{1.026m}})}^2}}} \end{array} $ | (19) |
式中:m为混凝土单轴抗压的率效应参数。将混凝土单轴抗压动态强度准则(16),单轴抗剪动态强度准则式(17),摩擦系数的率效应表达式(18),代入式(15),即可得到关于参数a, b, c的三元方程,求出参数a, b, c的值,如式(20)所示。
| $ \left\{ \begin{array}{l} \frac{{\sqrt 2 }}{3} = a + \frac{b}{3} + \frac{c}{9}\\ \frac{{\sqrt 6 {f_\tau }[{{(s{'_{\rm{d}}}/s{'_0})}^n}]}}{{3{f_{\rm{c}}}{{(s{'_{\rm{d}}}/s{'_0})}^{1.026m}}}} = a\\ \sqrt {\frac{{0.02}}{9} + \frac{{2{{({f_\tau }{{(s{'_{\rm{d}}}/s{'_0})}^n} + 0.1f'{{(s{'_{\rm{d}}}/s{'_0})}^k}{f_{\rm{c}}}{{(s{'_{\rm{d}}}/s{'_0})}^{1.026m}})}^2}}}{{3f_{{\rm{cd}}}^2}}}\\ = \frac{b}{{30}} + \frac{c}{{900}} \end{array} \right. $ | (20) |
针对设计强度C30,边长为300 mm的立方体试件,取文献[16]中混凝土在不同加载速率下的抗压强度数据,如表 3所示。将表 3的数据代入式(16)拟合得动态单轴抗压强度率效应参数m=0.053 74。
| 表 3 不同加载速率下混凝土抗压强度 Table 3 Compressive strength of concrete under different loading rates |
将数据代入式(17)和(18)拟合得n=0.02,k=0.000 7。文中fc=48.3 MPa,fτ=5.02 MPa,f'=1.371。
将上述数据代入式(20),求得a, b, c值如表 4。通过给出动态压剪共同作用强度准则模型与试验数据对比(如图 6)可以发现,二者吻合度很高,表明该动态强度准则的可靠性。但由于本文数据有限,只针对法向压力较小的情况,对于法向压力较大的情况还需进一步验证。
| 表 4 各加载速率下参数a, b, c计算结果 Table 4 Calculation results of a, b, c parameters under different loading rates |

|
图 6 本文模型与试验数据对比 Figure 6 Comparison between experimental data and data given by model of this paper under different loading rates |
为验证本文模型的适用性,将本文方法得到的结果与文献[13]的试验数据进行对比分析。通过Getdata软件获取文献[13]中的数据,导出的混凝土试件压剪强度见表 5。
| 表 5 不同工况下的压剪强度 Table 5 Compressive shear strength values under different working conditions |
文献[13]中,作者未列出混凝土抗压强度,故针对文献[12]中的抗压强度作为补充。文献[12]中的混凝土试件也由大连理工大学制备,且试件类型、尺寸、配合比以及试验所用仪器均相同,得到应变速率为10-5/s,10-4/s,10-3/s,10-2/s时的抗压强度fc分别为16.99,17.85,18.47和19.29 MPa。
将以上数据代入式(16),经拟合得m值为0.022 76。进而可得到加载速率分别为0.1,1.0及10.0 mm/s的混凝土相应的抗压强度为18.51,19.54和20.62 MPa。
取文献[13]中法向压力为0,1和2 MPa时的压剪强度值按式(18)进行线性拟合,求得加载速率为0.1,1.0和10.0 mm/s下的摩擦系数f'分别为1.239,1.315和1.415。
将混凝土抗剪强度、单轴抗压强度、摩擦系数以及相关速率效应参数m, n, k代入式(20),可以求得不同加载速率下的参数a, b, c的值,计算结果见表 6。
| 表 6 各参数计算结果 Table 6 Calculation results of each parameter |
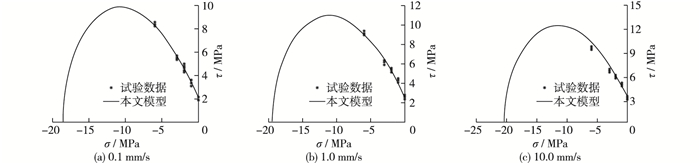
根据表 6中的a, b, c值,绘制出不同加载速率下强度准则曲线与试验数据对比,如图 7所示。可见,本模型计算得到结果与试验数据吻合度较高,从而证明了本文模型的准确性。对比试验数据结果发现,曲线变化趋势相同,但由于本文试件尺寸更大,加载速率更快,故试验结果在峰值点和横轴交点在数值上远大于文献[13]中的试验数据曲线。
|
图 7 不同加载速率下试验数据与本文模型对比 Figure 7 Comparison between experimental data and data given by model of this paper |
混凝土剪切强度随法向压力增大呈线性分阶段增大,法向压力不超过8 MPa时剪切强度增幅近似呈直线,当法向压力超过8 MPa时,增幅开始减小。随着加载速率的增加,混凝土抗剪强度随之增大,但相对于法向压力对抗剪强度的影响,其增幅微小。动态压剪作用下混凝土抗剪强度提高的主要因素是法向压力的增加。随着法向压力增加,混凝土率效应逐渐增加。基于Bresler-Pister静态强度准则提出的混凝土动态压剪强度准则与试验数据吻合较好,可为动态压剪作用下混凝土强度准则的提出提供参考。
| [1] |
肖建庄, 袁俊强, 李龙. 模型再生混凝土单轴受压动态力学特性试验[J]. 建筑结构学报, 2014, 35(3): 201-207. ( XIAO Jianzhuang, YUAN Junqinag, LI Long. Experimental study on dynamic mechanical behavior of modeled recycled aggregate concrete under uniaxial compression[J]. Journal of Building Structures, 2014, 35(3): 201-207. (in Chinese)) |
| [2] |
SU Y, LI J, WU C, et al. Influences of nano-particles on dynamic strength of ultra-high performance concrete[J]. Composites Part B Engineering, 2016, 91: 595-609. DOI:10.1016/j.compositesb.2016.01.044 |
| [3] |
CICHOCKI K, DOMSKI J, KATZER J, et al. Static and dynamic characteristics of waste ceramic aggregate fibre reinforced concrete[J]. Transactions of the Všb-Technical University of Ostrava Civil Engineering, 2015, 15(2): 1-14. |
| [4] |
张力伟, 赵颖华, 范颖芳, 等. 腐蚀混凝土损伤特征的声发射试验研究[J]. 建筑材料学报, 2013, 16(5): 763-769. ( ZHANG Liwei, ZHAO Yinhua, FAN Yinfang, et al. Damage investigation of corroded concrete under compression by AE test[J]. Journal of Building Materials, 2013, 16(5): 763-769. DOI:10.3969/j.issn.1007-9629.2013.05.005 (in Chinese)) |
| [5] |
AMIN A, FOSTER S J. Shear strength of steel fibre reinforced concrete beams with stirrups[J]. Engineering Structures, 2016, 111(5): 323-332. |
| [6] |
JACEK K, DOMSKI J. Static and dynamic characteristics of fibre reinforced WCA concrete[C]//Fibre Concrete, 2015. https://www.researchgate.net/publication/281740334_STATIC_AND_DYNAMIC_CHARACTERISTICS_OF_FIBRE_REINFORCED_WCA_CONCRETE
|
| [7] |
CEIA F, RAPOSO J, GUERRA M, et al. Shear strength of recycled aggregate concrete to natural aggregate concrete interfaces[J]. Construction and Building Materials, 2016, 109: 139-145. DOI:10.1016/j.conbuildmat.2016.02.002 |
| [8] |
俞茂宏. 混凝土强度理论及其应用[M]. 北京: 高等教育出版社, 2002. ( YU Maohong. Concrete strength theory and its application[M]. Beijing: Higher Education Press, 2002. (in Chinese))
|
| [9] |
俞茂宏. 强度理论百年总结[J]. 力学进展, 2004, 34(4): 529-560. ( YU Maohong. Advances in strength theories for materials under complex stress state in the 20th century[J]. Advances in Mechanics, 2004, 34(4): 529-560. DOI:10.3321/j.issn:1000-0992.2004.04.009 (in Chinese)) |
| [10] |
过镇海. 钢筋混凝土原理[M]. 北京: 清华大学出版社, 2012: 99. ( GUO Zhenhai. Principle of reinforced concrete[M]. Beijing: Tsinghua University Press, 2012: 99. (in Chinese))
|
| [11] |
梁兴文. 混凝土结构基本原理[M]. 重庆: 重庆大学出版社, 2012: 22. ( LIANG Xingwen. Basic principles of concrete structure[M]. Chongqing: Chongqing University Press, 2012: 22. (in Chinese))
|
| [12] |
闻伟.碾压混凝土单轴动态和压剪静态性能试验研究[D].大连: 大连理工大学, 2012. (WEN Wei. Experimental research on properties of RCC under uniaxial dynamic and compression-shear static stress states[D]. Dalian: Dalian University of Technology, 2012. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-1012394452.htm
|
| [13] |
王怀亮, 田平. 动态压剪作用下碾压混凝土强度和变形研究[J]. 水利与建筑工程学报, 2016, 14(2): 18-24. ( WANG Huailiang, TIAN Ping. Strength and deformation characteristics of RCC under dynamic compressive-shear loading[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(2): 18-24. DOI:10.3969/j.issn.1672-1144.2016.02.004 (in Chinese)) |
| [14] |
宋玉普, 闻伟, 王怀亮. 碾压混凝土压剪强度分析[J]. 水利与建筑工程学报, 2012, 10(6): 44-47. ( SONG Yupu, WEN Wei, WANG Huailiang. Analysis of compression-shear strength of roller compacted concrete[J]. Journal of Water Resources and Architectural Engineering, 2012, 10(6): 44-47. DOI:10.3969/j.issn.1672-1144.2012.06.011 (in Chinese)) |
| [15] |
李新钟, 魏雪英, 赵均海. 混凝土力学性能的应变率效应[J]. 长安大学学报(自然科学版), 2012, 32(2): 82-86. ( LI Xinzhong, WEI Xueying, ZHAO Junhai. Strain rate effect on mechanical properties of concrete[J]. Journal of Chang'an University (Natural Science Edition), 2012, 32(2): 82-86. DOI:10.3969/j.issn.1671-8879.2012.02.015 (in Chinese)) |
| [16] |
周洪涛.混凝土循环加卸载率效应特性研究[D].宜昌: 三峡大学, 2013. (ZHOU Hongtao. The study of dynamic behavior of concrete by cycle loading and unloading[D]. Yichang: China Three Gorge University, 2013. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D470827
|
2. College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China
 2018
2018 
