2. 水利部大坝安全管理中心,江苏 南京 210029
地震对水库大坝可能造成严重损坏。如何通过现场检查和监测资料,客观准确地评估大坝震损程度对大坝应急处置和除险加固具有重要意义。国内学者针对大坝震损评估的指标和方法做了大量工作。倪小荣等[1]建立了水库大坝震损综合评价指标体系,并采用关键指标评估了大坝震损程度;刘春辉等[2]利用灰色关联分析理论完善了土石坝震害评估经验统计模型;孙菲菲[3]分析了水库震损程度的指标,采用层次模糊综合评价法实现了中小型震损水库的评估;杨德玮等[4]以层次分析法为手段,研究了土石坝震损程度快速评估方法。以上研究中,选取的大坝震损评估指标繁多且复杂,指标权重计算主观性又较强,同时也未考虑相同指标在不同震损水库中严重程度不一的区别。
目前,层次分析法因其简单实用在确定指标权重的过程中被广泛采用,但也存在主观性较强的局限。另外,层次分析法确定的权重是普遍意义上的,即把各指标的权重视为定值(常权),而每个工程的特性及具体震损情况不同,因此相同指标在不同工程中的严重程度不一。当某个指标较为严重时,若直接套用常权进行评估,则该指标的严重程度可能被其他指标中和,致使评价系统的危险性降低和评估结果失真。而运用变权法可以根据不同工程中由各指标严重程度得出的指标评估值,对各指标的权重进行调整,从而得到更加切合实际的指标权重。
鉴于此,本文首先采用信息熵修正层次分析法(AHP)所得指标初始权重,降低主观性,然后考虑权重随指标严重程度的变化,建立基于信息熵-变权的土石坝震损模糊评估模型,并将其应用于实际震损土石坝的安全评估中。
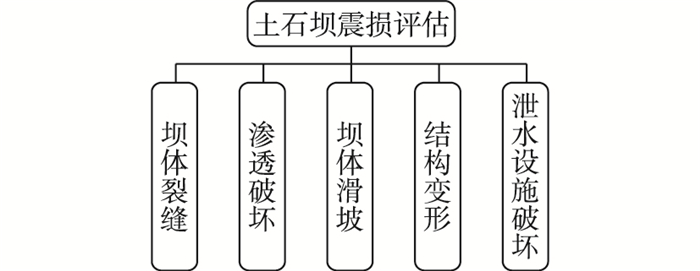
1 土石坝震损评估指标体系 1.1 指标体系构建根据国内外对震后土石坝震损情况的调查与统计分析[5-7],地震对土石坝造成的破坏险情主要包括裂缝、渗漏、滑坡、塌陷和泄水设施破坏等,由此建立土石坝震损评估指标体系(见图 1)。评估指标体系中包括5个指标,即坝体裂缝、渗透破坏、坝体滑坡、结构变形和泄水设施破坏。
|
图 1 土石坝震损评估指标体系 Figure 1 Seismic damage assessment index system for earth-rockfill dam |
考虑到已有的划分方法、相应的规范[8]和实践经验等多方面因素,将评估指标状况分为4级比较合适,指标评估集为[9]:V={υ1, υ2, υ3, υ4}={一般险情,严重险情,高危险情,溃坝险情}。参考文献[1]和[3]中指标阈值区间的划分标准,给出具体的指标等级划分和评分区间见表 1。
| 表 1 土石坝震损评估指标分级标准 Table 1 Grading standards of seismic damage assessment indexes for earth-rockfill dam |
层次分析法(AHP)是将指标定量化的有效方法,在缺少必要数据资料的情况下,借助专家知识和经验对指标进行量化较为实用。AHP法计算权重的流程如下:
(1) 构造判断矩阵根据建立的指标体系结构,运用表 2中1~9标度法得到判断矩阵A,其形式如表 3所示。
| 表 2 比率标度的含义 Table 2 Meaning of ratio scale |
| 表 3 判断矩阵A的一般结构 Table 3 General structure of judgement matrix A |
(2) 初始权重值计算。权重值计算过程为:①计算判断矩阵A中各行元素之积Mi:
(3) 判断矩阵的一致性检验。为了保证初始权重的准确性和可信度,须对判断矩阵进行一致性检验:
| $ CR = CI/RI $ | (1) |
式中:CI为一致性指标,CI=(λmax-n)/(n-1);λmax为判断矩阵A的最大特征根,
| 表 4 判断矩阵的RI取值 Table 4 RI values of judgement matrix |
当CR<0.1时,判断矩阵一致性检验满足要求;CR≥0.1时,需重新赋值修正,直至判断矩阵一致性检验满足要求。
需要说明的是,实际运用中可能有部分指标不存在,若认为不存在的指标无破坏,这样得出的结果势必会偏于安全,与实际情况不符。因此,在遇到指标不全存在的情况时,应当将未出现的指标剔除,然后再构造判断矩阵,计算其余指标初始权重。
2.2 信息熵修正初始权重尽管AHP方法识别问题的系统性较强,可靠性也相对较高,但主要基于专家经验,具有较强的主观色彩[11]。而熵权法作为一种客观赋权法,其计算结果客观、严谨,可以减小权重确定的主观性[12]。信息熵修正AHP法指标初始权重过程如下:
首先将判断矩阵A按下式进行归一化处理,其结果表示为:
| $ {q_{ij}} = {a_{ij}}/\sum\limits_{i = 1}^n {{a_{ij}}} $ | (2) |
| $ 定义第i项因素的熵值{e_i}为:{e_i} = - k\sum\limits_{i = 1}^n {{q_{ij}}\ln {q_{ij}}} $ | (3) |
式中:k>0,一般取k=1/lnn,i=1, 2, …, n。
| $ 定义第i项因素的熵权{\tau _i}为:{\tau _i} = \left( {1 - {e_i}} \right)/\sum\limits_{i = 1}^n {\left( {1 - {e_i}} \right)} $ | (4) |
利用τi修正AHP方法得到的指标初始权重ω0i,将修正后得到的权重记为ω1i:
| $ {\omega _{1i}} = {\tau _i}{\omega _{0i}}/\sum\limits_{i = 1}^n {({\tau _i}{\omega _{0i}})} $ | (5) |
式中:ω1i∈(0, 1),且∑ω1i=1。
经信息熵修正后得到的权重ω1i,可作为变权法计算的基础权重。
2.3 变权法计算原理经信息熵修正后得到的权重ω1i,主观性已经削弱,但仍是常权,为了体现各指标在实际工程中的严重程度对评估结果的贡献作用,采用变权法对权重ω1i进行调整,提高权重排序的科学性。
基于已选取的土石坝震损评估指标X=(x1,x2,…,xn)及指标分级标准,采用专家打分法,根据实际震损情况得出各指标评估值U=(u1,u2,…,un),其中ui∈[0, 1]。ui可以解释为对总体而言指标xi的安全可靠程度,并约定ui值越高,xi的安全可靠度越好[13],即指标严重性较低。并认为指标xi的权重依赖于各指标的评估值,则xi相对于总体而言的权重为ωi=ωi(u1,u2,…,un),其中ωi∈(0,1),且Σωi=1。利用变权法计算指标权重ωi的过程如下:
引入[0, 1]上定义的非负可微函数λi(u),使之满足λi'(u)≤0,并令:
| $ {\omega _i} = {\lambda _i}({u_i})/\sum\limits_{j = 1}^n {{\lambda _j}({u_j})} $ | (6) |
记λi(0)=λ2i,λi(1)=λ1i,且令λ1i=ω1i,则得:
| $ {\lambda _{2i}} = \frac{{{\omega _{2i}}\mathop \Sigma \limits_{j \ne i} {\omega _{1j}}}}{{1 - {\omega _{2i}}}} $ | (7) |
ω2i可按下式计算[14]:
| $ {\omega _{2i}} = \frac{{{\omega _{1i}}}}{{\mathop {\min }\limits_{1 \le j \le n} {\omega _{1j}} + \mathop {\max }\limits_{1 \le j \le n} {\omega _{1j}}}} $ | (8) |
由于dωi/dλi>0,dωi(u)/du≤0,故假定权重ωi的变化率与自身大小成正比,与指标评估值ui的ki(ki≤1)次方成反比,即在土石坝震损评估中,指标权重的变化与建筑物的重要性和水库当前的震损程度有关,故令:
| $ \frac{{{\rm{d}}{\lambda _i}\left( u \right)}}{{{\rm{d}}u}} = - \frac{{{\lambda _i}\left( u \right)}}{{\mathop \Sigma \limits_{j \ne i} {\lambda _{2j}}{u^{{k_i}}}}} $ | (9) |
由边值条件λi(0)=λ2i,λi(1)=ω1i,解式(9)得:
| $ {\lambda _i}\left( u \right) = {\lambda _{2i}}\exp \left( { - \frac{{{u^{1 - {k_i}}}}}{{(1 - {k_i})\mathop \Sigma \limits_{j \ne i} {\lambda _{2j}}}}} \right) $ | (10) |
其中,
| $ {k_i} = 1 + \frac{1}{{\mathop \Sigma \limits_{j \ne i} {\lambda _{2j}}\ln \frac{{{\omega _{1i}}}}{{{\lambda _{2i}}}}}} $ | (11) |
在变权法计算过程中,指标xi的权重ωi随着指标评估值ui的变小而增大,当ui=0,uj=1(i≠j)时(亦即指标xi的安全可靠性完全丧失,而其他指标的安全可靠性十分好),指标xi的权重达到最大值,这个过程即体现了震损评估中突出指标严重性程度的思想。
2.4 模糊综合评估模型通过信息熵修正和变权法调整后,指标权重ωi更为客观,且更能反映出不同指标在实际工程中的严重程度。基于此,采用模糊评价法对土石坝震损程度进行综合评估。
(1) 确定模糊关系矩阵。首先计算单个指标xi(i=1, 2, …, n)对评估等级υj(j=1, 2, …, m)的隶属度rij。rij表示第i个指标xi在第j个评估等级υj上的频率分布,从而得出第i个指标xi的单因素评判集ri=(ri1, ri2, …, rim);接着依次得出所有n个指标的评判集,并将其合并成一个总的评估关系矩阵R,即确定了从X到V的模糊关系R。
各指标的隶属度按以下隶属函数计算。拟定的各隶属函数为线性函数,且满足:若rvj(ui)=1,则rvj-1(ui)=rvj+1(ui)=0[15],如图 2所示。

|
图 2 rvj的线性隶属函数 Figure 2 Linear membership functions of rvj |
隶属函数的表达式如下:
| $ {r_{{v_{_1}}}}\left( \mu \right) = \left\{ \begin{array}{l} \left( {0.4 - \mu } \right)/0.2, \;\;\;u \in \left[ {0.2, 0.4} \right]\\ 1.0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u \in \left[ {0, 0.2} \right]\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (12) |
| $ {r_{{v_{_2}}}}\left( \mu \right) = \left\{ \begin{array}{l} \left( {u-0.2 } \right)/0.2, \;\;\;u \in \left[ {0.2, 0.4} \right]\\ \left( {0.6-u } \right)/0.2, u \in \left[ {0.4, 0.6} \right]\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (13) |
| $ {r_{{v_{_3}}}}\left( u \right) = \left\{ \begin{array}{l} \left( {u-0.4 } \right)/0.2, \;\;\;u \in \left[ {0.4, 0.6} \right]\\ \left( {0.8-u } \right)/0.2, u \in \left[ {0.6, 0.8} \right]\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (14) |
| $ {r_{{v_{_4}}}}\left( u \right) = \left\{ \begin{array}{l} \left( {u-0.6 } \right)/0.2, \;\;\;u \in \left[ {0.6, 0.8} \right]\\ 1.0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;u \in \left[ {0.8, 1.0} \right]\\ 0, \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;其他 \end{array} \right. $ | (15) |
(2) 模糊综合评估。为了与评估指标的分级标准相对应,将最终的土石坝震损程度也分为4个等级,即一般险情、严重险情、高危险情和溃坝险情。
在模糊评价关系矩阵R中,不同的行反映了各指标对各评价子集的隶属程度。用权重ωi与矩阵R作合成计算,即可得到震损程度对各评估子集的隶属度,即模糊综合评估结果向量B,计算公式为:
| $ {b_j} = \sum\limits_{i = 1}^n {{\omega _i}{r_{ij}}} $ | (16) |
式中:bj为模糊综合评估结果向量B中的元素;ωi为指标xi的权重;rij为评估矩阵R的元素,rij∈[0, 1]。
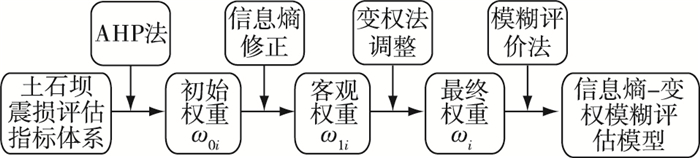
最后根据bj值的大小,按照“最大隶属度”原则,确定土石坝震损等级。图 3为基于信息熵-变权模糊的土石坝震损评估模型建立流程。
|
图 3 信息熵-变权模糊评估模型建立流程 Figure 3 Flow chart of information entropy-variable weight fuzzy model |
某水库正常蓄水位为594.20 m,总库容为170万m3,属小(1)型水库。主要建筑物由大坝、溢洪道、放水设施等组成。大坝为均质土坝,坝顶高程597.80 m,最大坝高18.4 m,坝顶宽4.4 m,长91.0 m。溢洪道位于大坝左岸,为开敞式正槽溢洪道,放水设施为左右两岸的放水涵管。
该水库于2008年遭遇了“5.12”汶川地震,震后发现大坝出现了裂缝及严重的管涌现象,主要震损险情有:(1)裂缝。据震后现场检查,发现坝顶有一条纵向裂缝,长约30 m,宽3~4 cm,深达2 m;大坝左中部一条横向裂缝,长2~3 m, 地表裂缝宽2~3 cm,深3~4 m。(2)渗漏。地震前,库水位593.85 m,渗流量微小。震后现场检查时发现大坝下游坝脚渗漏量加大,且发生了严重的管涌现象,共5处,自左至右为:①1#涌水点距左坝肩30 m,浑浊度较大,且流量较大;②2#涌水点距左坝肩37 m,有明显浑浊水流出;③3#涌水点距左坝肩37.5 m,有明显浑浊水流出,且流量较大;④4#涌水点距左坝肩44 m,有明显浑浊水流出,且流量较大;⑤5#涌水点距左坝肩47 m,流量较大。上述5处的管涌水量共达0.3 m3/s左右。(3)防浪墙震损。有多条裂缝。(4)泄水设施破坏。左岸放水涵管裂缝或脱离坝体,溢洪道陡坡段下部出现渗漏现象,水较浑浊。
3.2 权重确定及调整首先根据层次分析法确定各指标的初始权重,从水库实际震损情况可知,该水库震后未出现滑坡险情,故将“坝体滑坡”指标剔除。在综合有关专家意见基础上,经计算得到ω0i=(0.393 7 0.393 7 0.137 4 0.075 2)。AHP法判断矩阵的构造及一致性检验见表 5。
| 表 5 指标初始权重及信息熵修正后的权重 Table 5 Index initial weight and corrected weight of information entropy |
利用信息熵对初始权重ω0i进行修正,即得修正后的权重为ω1i=(0.391 3 0.391 3 0.150 4 0.067 0),见表 5。
根据该水库实际震损情况,由专家基于指标分级标准,得出各指标评估值为U0=(0.78 0.90 0.45 0.70)。由于变权法中约定“ui值越高,xi的安全可靠度越好”,而按本文指标分级标准得出的指标评估值越大则险情越大,因此为了与变权法思想一致,故需将1-U0作为变权计算中的U,即得U=1-U0=(0.22 0.10 0.55 0.30)。由ui,ω1i并根据式(6),(8),(11)以及(10)分别计算出ω2i,λ2i,ki,λi,然后将λi代入式(7)即可得出变权后的权重ωi,计算结果见表 6。
| 表 6 变权法计算结果 Table 6 Calculation results given by variable weight method |
经变权法调整后的权重为ωi=(0.383 7 0.448 1 0.113 9 0.054 3),相较于ω1i,“渗透破坏”指标的权重由0.391 3增至0.448 1,明显大于其他指标权重,与该水库震后出现了严重的管涌险情相符,从而突出了“渗透破坏”这一指标的严重程度,亦即该指标评估值对震损程度评估的影响。
3.3 模糊关系矩阵建立根据各指标评估值U0=(0.78 0.90 0.45 0.70),按隶属函数式(12)~(15)分别计算各指标对各评估等级的隶属度,最后得到模糊关系矩阵R:
| $ \mathit{\boldsymbol{R}} = \left[ {\begin{array}{*{20}{c}} 0&0&{0.40}&{0.60}\\ 0&0&0&{1.00}\\ 0&{0.75}&{0.25}&0\\ 0&0&{0.50}&{0.50} \end{array}} \right] $ | (17) |
将变权法调整后得到的权重ωi与R进行合成,由式(16)计算出综合评估结果向量为B=(0 0.085 40.209 1 0.705 5),其中最大值为b4=0.705 5,根据最大隶属度原则,该水库震损程度评为“溃坝险情”。而根据《四川省德阳市震后受损水库核查报告》,该水库震损等级属于“溃坝”等级,与本文评估结果一致。
为便于比较,将变权调整前的权重ω1i与R合成,得出综合评估结果向量为B′=(0 0.112 8 0.227 60.659 6),按最大隶属度原则,亦可确定该水库震损等级为“溃坝险情”。由于渗漏对土石坝安全有重要影响,且该水库震后出现了严重的管涌险情,相反其他指标严重性相对较低,经变权计算后“渗透破坏”这一指标的权重增加,而其他指标权重降低。因此通过比较B与B′中元素可知,B中元素更能体现出各指标的严重程度,使评估结果B与水库实际震损状态更为切合。
4 结语阐述了土石坝震损评估指标体系及指标分级标准,将AHP、信息熵和变权法进行融合,建立了基于信息熵-变权模糊的土石坝震损评估模型。通过工程算例表明,该模型削弱了AHP法确定指标权重过程中的主观性,并体现了指标严重程度(指标评估值)对土石坝震损评估的影响,使土石坝震损评估结果更加客观科学。
指标评估值的确定含有专家主观因素,如何更加客观地确定指标评估值还有待进一步研究。
| [1] |
倪小荣, 王士军, 谷艳昌. 基于关键指标的水库大坝震损程度综合评价体系[J]. 水利水运工程学报, 2010(4): 27-32. ( NI Xiaorong, WANG Shijun, GU Yanchang. Comprehensive evaluation of earthquake damage degree of reservoir dam based on key indexes[J]. Hydro-Science and Engineering, 2010(4): 27-32. DOI:10.3969/j.issn.1009-640X.2010.04.006 (in Chinese)) |
| [2] |
刘春辉, 景冰冰, 李永强. 土石坝震害快速评估方法研究[J]. 地震工程与工程振动, 2013, 33(2): 156-162. ( LIU Chunhui, JING Bingbing, LI Yongqiang. Study on rapid assessment methods for seismic damage to earth-rock dams[J]. Earthquake Engineering and Engineering Vibration, 2013, 33(2): 156-162. (in Chinese)) |
| [3] |
孙菲菲.中小型水库震损险情综合评价指标体系研究[D].沈阳: 沈阳农业大学, 2013. (SUN Feifei. Comprehensive evaluation index system of earthquake damage of small and medium sized reservoir[D]. Shenyang: Shenyang Agricultural University, 2013. (in Chinese))
|
| [4] |
杨德玮, 张士辰, 王昭升. 土石坝震损程度快速评估方法研究[J]. 水利与建筑工程学报, 2016, 14(1): 107-111, 154. ( YANG Dewei, ZHANG Shichen, WANG Zhaosheng. Rapid assessment method of seismic damage degree for earth dam[J]. Journal of Water Resources and Architectural Engineering, 2016, 14(1): 107-111, 154. DOI:10.3969/j.issn.1672-1144.2016.01.020 (in Chinese)) |
| [5] |
王士军, 谷艳昌, 倪小荣, 等. 震后水库大坝应急检查[J]. 中国水利, 2012(6): 35-37. ( WANG Shijun, GU Yanchang, NI Xiaorong, et al. Emergency inspection of reservoir dam after earthquake[J]. China Water Resources, 2012(6): 35-37. DOI:10.3969/j.issn.1000-1123.2012.06.015 (in Chinese)) |
| [6] |
CHEN Guoxing, JIN Dandan, MAO Jin, et al. Seismic damage and behavior analysis of earth dams during the 2008 Wenchuan earthquake, China[J]. Engineering Geology, 2014, 180: 99-129. DOI:10.1016/j.enggeo.2014.06.001 |
| [7] |
YAMAHUCHIN Y, KONDO M, KOBORI T. Safety inspections and seismic behavior of embankment dams during the 2011 off the Pacific Coast of Tohokuearthquake[J]. Soils and Foundations, 2012, 52(5): 945-955. DOI:10.1016/j.sandf.2012.11.013 |
| [8] |
SL 450—2009堰塞湖风险等级划分标准[S]. (SL 450—2009 Standard for classification of risk grade of landslide lake[S]. (in Chinese))
|
| [9] |
张建云, 杨正华, 蒋金平, 等. 水库大坝病险和溃坝的研究与警示[M]. 北京: 科学出版社, 2014. ( ZHANG Jianyun, YANG Zhenghua, JIANG Jinping, et al. A study on reservoir dam defects and breaches in China[M]. Beijing: Science Press, 2014. (in Chinese))
|
| [10] |
许树柏. 层次分析法原理[M]. 天津: 天津大学出版社, 1988. ( XU Shubai. Principles of analytic hierarchy process[M]. Tianjin: Tianjin University Press, 1988. (in Chinese))
|
| [11] |
谷艳昌, 王士军. 土石坝突发事件预警因子识别技术研究[J]. 水利水电技术, 2010, 41(10): 73-75. ( GU Yanchang, WANG Shijun. Study on identifying technology of early-warning index of emergency events for earth-rockfill dam[J]. Water Resources and Hydropower Engineering, 2010, 41(10): 73-75. DOI:10.3969/j.issn.1000-0860.2010.10.018 (in Chinese)) |
| [12] |
刘愚. 基于熵权—理想点法的大坝安全评价模型及应用[J]. 水电能源科学, 2016, 34(5): 73-76. ( LIU Yu. Dam safety evaluation model and its application based on entropy weight and ideal point method[J]. Water Resources and Power, 2016, 34(5): 73-76. (in Chinese)) |
| [13] |
江沛华, 汪莲. 基于变权的多层次模糊综合评判在大坝安全评价中的应用[J]. 中国农村水利水电, 2010(4): 112-114. ( JIANG Peihua, WANG Lian. Application of multi level fuzzy comprehensive evaluation based on variable weight in dam safety evaluation[J]. China Rural Water and Hydropower, 2010(4): 112-114. (in Chinese)) |
| [14] |
彭祖赠, 孙韫玉. 模糊(Fuzzy)数学及其应用[M]. 2版. 武汉: 武汉大学出版社, 2007. ( PENG Zhuzeng, SUN Wenyu. Fuzzy mathematics and its application[M]. 2nd ed. Wuhan: Wuhan University Press, 2007. (in Chinese))
|
| [15] |
王志涛, 江超, 姜晓琳, 等. 基于模糊理论的土石坝风险综合评价方法研究[J]. 水利与建筑工程学报, 2011, 9(2): 27-30, 105. ( WANG Zhitao, JIANG Chao, JIANG Xiaolin, et al. Research on comprehensive evaluation method for risk of earth-rock dam based on fuzzy logic[J]. Journal of Water Resources and Architectural Engineering, 2011, 9(2): 27-30, 105. DOI:10.3969/j.issn.1672-1144.2011.02.007 (in Chinese)) |
2. Dam Safety Management Center of the Ministry of Water Resources, PRC, Nanjing 210029, China
 2018
2018 