2. 武汉大学水利水电学院,湖北 武汉 430072
变形监控指标用来评估和监控大坝安全的标准,对工程安全起着重要的参考作用。而拟定监控指标的关键是通过大坝在历史荷载作用下的抵御能力来预测和估计抵抗未来可能产生较大荷载的能力,并在该荷载组合下确定监控效应量的预警值或极值[1-2]。
目前拟定大坝变形监控指标主要包含两条途径,一是基于已有的监测效应量,采用数学分析方法挖掘大坝蕴含的变形信息,如置信区间估计法、典型监测效应量的小概率法等[1];二是从坝体及坝基的力学性态角度进行结构计算获取变形极值。由于采用数学分析方法拟定大坝变形监控指标比较方便,尤其是基于长期监测资料序列拟定的一级变形监控指标具有良好的预警作用。因此,基于监测效应量,采用数学分析方法拟定变形监控指标在大坝工程中应用较广泛。研究表明,传统方法(如典型小概率法和置信区间法)在拟定大坝安全监控指标时需大量的监测数据样本,且母本的分布类型需通过子样的分布情况来确定,这样使得监控指标拟定较复杂。近年来,国内外提出了多种监控模型进行大坝安全监测资料分析[3-5],并考虑模糊性、混沌性及事件发生概率等因素,建立监控指标拟定模型。例如,从样本数据特征值角度出发,无需子样分布的最大熵法直接根据样本数字特征值确定概率密度函数[6]进而拟定变形监控指标;此外,由于大坝变形监测效应量影响因素较复杂,为此引入了充分考虑大坝工作性态的模糊性与随机性的云模型法,建立大坝出现险情的确定度与监测效应量之间的非线性映射关系[7]。虽然上述两种方法在变形监控指标拟定的应用中取得了良好效果,但目前关于这两种方法拟定的变形监控指标差异尚未见文献报导。此外,在监控指标拟定中,异常概率一般依据工程重要性确定,具有较大的人为主观因素。
针对上述问题,本文以高寒地区某RCC坝典型挡水坝段为例,首先引入改进的快速Myriad滤波法对该坝段坝顶位移监测值进行预处理,然后对比研究了基于最大熵法和云模型法分别拟定大坝变形监控指标的差异性,最后探讨了异常概率与云模型弱外围元素对定性概念贡献率之间的关系。
1 云模型法拟定变形监控指标原理 1.1 基本原理云模型能反映出生活中的概念性与随机性,实质上讲,它是定性概念与定量表示之间相互转化的一种不确定性模型[8]。本文将云模型应用于大坝安全监控领域,原理如下:
设C为监测对象(大坝)的效应量对应的定量论域,Q为C上的安全状态评判,若定量值x∈C,且x为Q中监测对象(大坝)的一次随机实现,x关于Q的确定度μ(x)∈[0, 1]具有稳定的随机分布规律:
| $ \mu :C \to \left[ {0, 1} \right]\;\forall x \in C, x \to \mu \left( x \right) $ | (1) |
式中:x在C上的分布称为云,x称为云滴。
在计算分析时,首先基于逆向云发生器,确定样本的期望、熵及超熵(Ex, En, He),实现样本特征的定性;然后据此通过正向云发生器获得需要的正态随机数,最终确定监测数据xi的云滴群分布,实现了样本特征的定量。以ui作为监测数据xi的确定度,它代表了某种倾向的稳定程度,在图形上主要表现为云滴是否集中。对于监测序列中每个数据xi而言,(xi, ui)便为论域C中的某个云滴的联合概率。本文将常见的“钟形”函数形式u=exp(-(x-a)2/(2b2))(a, b为常量)作为云滴xi隶属度。
1.2 云滴对定性的概念云滴群在数据范围内的概念贡献率不同,下面给出云滴群对定性概念贡献率定义,即论域中对任意区间的Δx对定性概念A的贡献ΔC为
| $ \mathit{\Delta }C \approx {\mu _A}\left( x \right)\mathit{\Delta }x/(\sqrt {2{\rm{ \mathsf{ π} }}} {E_n}) $ | (2) |
式中:
由云滴群分布和式(2)可知,论域中定性概念贡献率较大的云滴群大多分布在[Ex-3En, Ex+3En]范围内,而在此区间外的云滴对定性概念贡献率仅为0.26%,由此可见这些云滴基本可以忽略,故将贡献率最大的区间范围[Ex-3En, Ex+3En]作为正向云模型的“3En规则”,由此可以认为非定性概念表征出异常信息。
不同区间范围内的云滴占定性概念的总贡献率比例不同,其中“弱外围元素”:表示对称分布区间[Ex-3En, Ex+2En],[Ex-2En, Ex+3En]内的云滴群,它们对定性概念的总贡献率为4.30%,对称区间各占2.15%。
由于变形监控指标拟定的异常概率具有模糊性和随机性,而云模型弱外围元素对定性概念贡献率具有相对明确的理论依据,为此,一方面探讨不同方法拟定变形监控指标的差异,另一方面还探讨变形监控指标拟定的异常概率与云模型弱外围元素对定性概念贡献率之间的关系。
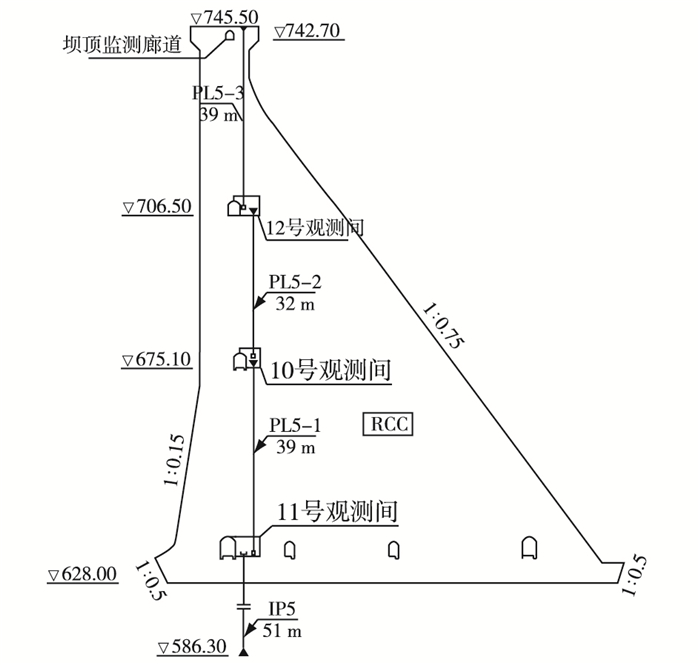
2 实例分析 2.1 工程概况某大型水利枢纽工程位于西北高寒地区,主要由大坝、发电引水系统、电站厂房以及副坝等许多水工建筑物组成。该工程为Ⅰ等大(1)型工程,枢纽水库总库容24.19亿m3,水库正常蓄水位739.00 m,死水位680.00 m。拦河大坝为全断面碾压混凝土重力坝,主坝最大坝高121.50 m。35#挡水坝段为典型监测坝段,该坝段共布置3条正垂线和1条倒垂线,即正垂线测点PL5-1,PL5-2和PL5-3分别布置在高程675.10,706.50和742.70 m处,坝基倒垂线测点IP5锚固在高程586.30 m处,监测断面具体情况见图 1。本文以该坝段为例,依据坝顶测点PL5-3的实测位移,由最大熵法和云模型法拟定坝顶位移变形监控指标,并对这两种方法拟定的变形监控指标进行对比分析。
|
图 1 监测断面(单位:m) Figure 1 Monitoring section (unit: m) |
针对实际工程中的监测数据往往存在不真实噪声的现象,为保证监控指标拟定的准确性,采用改进的Myriad滤波法[9-11]对坝顶测点监测数据进行预处理。Myriad滤波器应用较广泛,不仅对实测的高斯分布有效果,而且对多领域中的经仪器监测到的复杂柯西数据分布甚至稳态数据分布都具有较好的控制作用。这种广泛的适用性使Myriad滤波器能够在复杂多变的噪声环境中提取实际工程中真实的监测信息。Myriad滤波以滑动窗口作为计算单元,由窗口内监测数据经过滤波得到计算结果,其中合理的线性度参数k与窗口单元数m作为重要参数。为确定其值,引入信噪比对原型监测数据的滤波效果进行评价,即对线性度参数、窗口长度进行敏感性分析,找出信噪比趋近于收敛时对应的线性度参数、窗口长度。信噪比SNR由下式定义:
| $ {S_{{\rm{NR}}}} = 10\lg (\sigma _{\rm{S}}^2/\sigma _{\rm{N}}^2) $ | (3) |
式中:σS2为去噪后的监测信息方差;σN2为从监测信息中滤出的含有噪声信息的方差。
以坝顶测点为例,对变化的窗口进行敏感性分析。在监测数据处理前,选取窗口计算长度m=5~9,线性度参数k=0.1~80.0,由此基于监测序列对这两个特征参数进行分析,计算结果见图 2。

|
图 2 各参数关系曲线 Figure 2 Relationship curves of parameters |
由图 2可知,从横向来看,当线性度参数k<1.0时,信噪比随线性度参数的增大而逐渐减小,但变化程度不是很明显;而当k>1.0时,信噪比随着线性度参数的增大而逐渐增大,增大到一定程度,逐渐收敛于稳定值;从纵向来看,窗口长度越长,信噪比越小,滤除的噪声方差较大,此时越不稳定;反之,去噪效果则越好。
当线性度参数k=20.0时,信噪比已收敛,考虑运算量及计算效率,选取计算窗口长度m=5,此时信噪比为14.86 dB。坝顶测点的原始数据处理前后效果对比见图 3。

|
图 3 坝顶测点原始监测数据与滤波数据对比 Figure 3 Comparison between original monitoring data and filter data of top measuring points |
由图 3可知,含噪数据中随机噪声几乎全部减小,后期监测数据滤波较明显,这说明快速Myriad滤波处理含有噪声的监测数据效果较好。
2.3 基于坝顶测点的变形监控指标拟定 2.3.1 坝顶测点监测序列极值统计基于现场采集的监测资料统计分析该工程典型坝段坝顶测点PL5-3每年位移的最大值。由于坝顶测点监测资料系列较短,为便于反映坝顶测点变形,故给出每月份位移极值(见表 1)。
| 表 1 坝顶测点水平位移极值 Table 1 Extreme situation of top measuring points of horizontal displacement |
由于坝顶测点监测数据的原点矩较大,为此将位移监测序列子样转化为(x-δ)/σ样本[12],获得各测点相应的最大熵概率密度函数系数及样本数字特征值[13]。即首先计算样本的原点矩μi(i=1, 2, 3, 4),然后依据最大熵概率密度函数原理,求得其函数表达式,进而采用Newton迭代法[14]优化求解获得λi(i=1, 2, 3, 4),进而结合式(4)获得λ0。
| $ f\left( x \right) = \exp ({\lambda _0} + \sum\limits_{i = 1}^n {{\lambda _i}{x^i}} ) $ | (4) |
基于监测效应量的最大熵概率函数系数及特征值见表 2。令xm为大坝变形监控指标或极值,则大坝出现异常的概率为:
| 表 2 数字特征值及函数系数 Table 2 Digital eigenvalues and function coefficients |
| $ {P_a} = \smallint _{{x_m}}^{^{ + \infty }}f\left( x \right){\rm{d}}x\;\;\;\;\;x > {x_m} $ | (5) |
由于大坝位移测值出现异常的概率很小,结合工程结构重要性,异常概率一般为1%或5%,然后根据上式中的逆累积分布函数的性质,可得PL5-3测点变形监控指标值为18.228 mm(α=1%),17.749 mm(α=5%), 18.026 mm(α=2.15%), 特征值δ=15.580,σ=1.473。
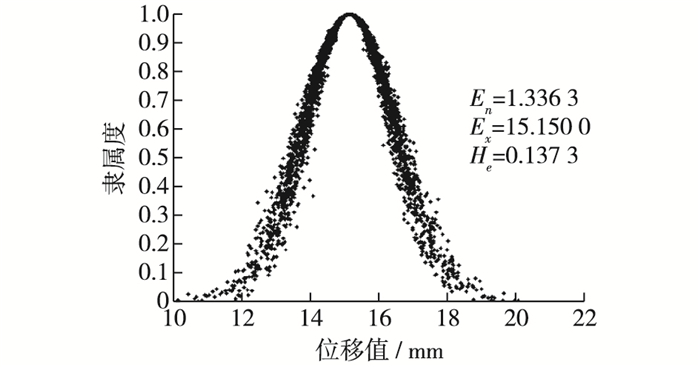
2.3.3 云模型法拟定变形监控指标为充分考虑不利工况下极值,选取大坝运行期出现高水位(730.00 m附近)时的监测序列分析。首先设置N=3 000个云滴,基于无确定度的云模型逆向云发生器触发机制计算坝顶测点位移的3个数字特征值;然后采用正向云发生器触发机制计算形成正态随机数,最终确定监测数据X={x1, x2, …, xn}的云滴,实现了定量-定性的转换。最后采用云滴对定性概念中“3En规则”拟定变形监控指标。基于matlab平台编制了云模型计算程序,得到样本3 000个云滴及相应的隶属度,以坝顶测点为例,具体见图 4。
|
图 4 坝顶测点位移云滴群 Figure 4 Displacement cloud drop group of top measuring points |
根据云模型中云滴对监控指标概念的定义,按照“3En规则”,拟定的变形指标极大值为Ex+3En。而根据概念贡献定义划分,“弱外围元素”较大端点极值为Ex+2En,此时“弱外围元素”中极大值部分对定性概念的贡献率约为2.15%。由此得到坝顶测点变形监控指标,见表 3。
| 表 3 基于云模型的变形指标 Table 3 Deformation index based on cloud model |
基于坝顶测点的监测效应量,采用最大熵法、云模型法分别拟定了大坝变形监控指标。分析表明:基于监测效应量,最大熵法按异常概率为1%与5%拟定的变形监控指标与云模型法按“3En准则”拟定的变形监控指标存在一定差异。
根据监测资料,坝顶测点PL5-3实测变形最大值为17.50 mm,小于拟定的安全监控指标,说明大坝目前处于正常运行状态。
2.4 基于云模型确定异常概率方法的探讨在拟定大坝变形监控指标时,需要确定异常概率的大小。异常概率的确定一般依据工程重要性来确定,选取时基于人为经验假定为1%或5%。显然,异常概率的确定具有模糊性与随机性。故考虑采用云模型中云滴对定性概念的贡献率来近似反映异常概率的取值,即采用云模型中的“弱外围元素”范围内的监测值,此时,云滴对定性概念总贡献率仅为4.30%,极大值附近的云滴对定性概念的贡献则为2.15%,故此基于最大熵法得到异常概率为2.15%的坝顶测点PL5-3的变形监控指标18.026 mm,此时拟定的监控指标与云模型按“弱外围元素”拟定变形监控指标17.823 mm较为接近。由此可认为云模型中较大的“弱外围元素”对定性概念贡献率与变形监控指标拟定的异常概率具有相似性,从而为变形监控指标拟定的异常概率确定提供参考。
3 结语(1) 云模型法按“3En准则”拟定的变形监控指标与最大熵法按照异常概率为1%与5%拟定的变形监控指标存在一定差异,二者均通过数字特征值进行计算,包含的主观成分少,拟定的变形监控指标更可信。由监测数据可知,坝顶测点变形实测最大值均小于两种方法下的变形监控指标拟定值,说明大坝目前处于正常运行状态。
(2) 针对确定异常概率具有模糊性与随机性的问题,考虑采用云模型中云滴对定性概念的贡献率来近似反映异常概率的取值,由此可认为云模型中较大的“弱外围元素”对定性概念贡献率与变形监控指标拟定的异常概率具有相似性,从而为确定异常概率寻找到一种方法。
(3) 由于变形监控指标是由大坝和坝基已经抵御经历荷载的能力拟定,而大坝的工作性态受外界环境因素的影响随着时间不断演化,因此有必要待该碾压混凝土重力坝运行一段时间后,再做进一步分析和监控指标拟定。
| [1] |
吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003. ( WU Zhongru. Safety monitoring theory and its application of hydraulic structures[M]. Beijing: Higher Education Press, 2003. (in Chinese))
|
| [2] |
SU H Z, WEN Z P, WU Z R. Study on an intelligent inference engine in early-warning system of dam health[J]. Water Resources Management, 2011, 25(6): 1545-1563. DOI:10.1007/s11269-010-9760-3 |
| [3] |
戴波, 何启. 大坝变形监测统计模型与混沌优化ELM组合模型[J]. 水利水运工程学报, 2016(6): 9-15. ( DAI Bo, HE Qi. A model combining with statistic model and chaos-optimized extreme learning machine for dam deformation monitoring[J]. Hydro-Science and Engineering, 2016(6): 9-15. (in Chinese)) |
| [4] |
罗德河, 郑东健. 大坝变形的小波分析与ARMA预测模型[J]. 水利水运工程学报, 2016(3): 70-75. ( LUO Dehe, ZHENG Dongjian. Wavelet analysis and ARMA prediction model for dam deformation[J]. Hydro-Science and Engineering, 2016(3): 70-75. (in Chinese)) |
| [5] |
李萌, 包腾飞, 杨建慧, 等. 灰色模型改进的大坝变形分形几何监控模型[J]. 水利水运工程学报, 2016(4): 104-110. ( LI Meng, BAO Tengfei, YANG Jianhui, et al. Fractal geometry monitoring model for dam deformation based on improved grey model[J]. Hydro-Science and Engineering, 2016(4): 104-110. (in Chinese)) |
| [6] |
丛培江, 顾冲时, 谷艳昌. 大坝安全监控指标拟定的最大熵法[J]. 武汉大学学报(信息科学版), 2008, 33(11): 1126-1129. ( CONG Peijiang, GU Chongshi, GU Yanchang. Maximum entropy method for determining dam safety monitoring indices[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1126-1129. (in Chinese)) |
| [7] |
朱凯, 秦栋, 汪雷, 等. 云模型在大坝安全监控指标拟定中的应用[J]. 水电能源科学, 2013, 31(3): 65-68. ( ZHU Kai, QIN Dong, WANG Lei, et al. Application of cloud model in determining dams safety monitoring index[J]. Water Resources and Power, 2013, 31(3): 65-68. (in Chinese)) |
| [8] |
LI D Y, LIU C Y, GAN W Y. A new cognitive model: cloud model[J]. International Journal of Intelligent Systems, 2009, 24(3): 357-375. DOI:10.1002/int.v24:3 |
| [9] |
SHAO M, NIKIAS C L. Signal processing with fractional lower order moments: stable processes and their applications[J]. Proceeding of the IEEE, 1993, 81(7): 986-1010. DOI:10.1109/5.231338 |
| [10] |
YUE B, PENG Z M, HE Y M, et al. Impulsive noise suppression using fast Myriad filter in seismic signal processing[C]//Expanded Abstracts of 5th International Conference on Computational and Information Science(ICCIS), 2013: 1001-1004. http://dl.acm.org/citation.cfm?id=2548936
|
| [11] |
GOH B M K, LIM H S. Sequential algorithms for sample Myriad and weighted Myriadfilter[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 6047-6052. DOI:10.1109/TSP.2012.2208959 |
| [12] |
黄耀英. 大坝安全监控正反分析方法与优化调控[M]. 北京: 中国水利水电出版社, 2016. ( HUANG Yaoying. Forward and back analysis methods and optimal control of safety monitoring in dams[M]. Beijing: China Water & Power Press, 2016. (in Chinese))
|
| [13] |
JAYNES E T. Information theory and statistical mechanics[J]. Physics Rev, 1957, 106(4): 620-630. DOI:10.1103/PhysRev.106.620 |
| [14] |
龚纯, 王正林. 精通MATLAB最优化计算[M]. 北京: 电子工业出版社, 2012. ( GONG Chun, WANG Zhenglin. Proficient in MATLAB optimization calculation[M]. Beijing: Publishing House of Electronic Industry, 2012. (in Chinese))
|
2. School of Water Resources and Hydropower Engineering, Wuhan University, Wuhan 430072, China
 2018
2018 

