工程中岩体的破坏大多沿着节理裂纹发生,节理的抗剪性质对岩体的整体稳定和安全至关重要,因此近些年一直受到国内外学者的密切关注。Barton等[1-2]对不同粗糙度天然岩石节理的力学性质进行了试验研究,建立了著名的JRC-JCS模型来预测单一节理的抗剪强度。赵坚[3]提出了吻合度系数JMC来描述节理间的接触状态,并对JRC- JCS模型进行了修正。李海波等[4-5]用水泥砂浆节理试样进行了不同剪切速率下的直剪试验,总结得到了含有剪切速率参数的抗剪强度公式。朱小明等[6]用含有一、二阶起伏体的石膏节理试样进行了直剪试验,发现节理二阶起伏体对节理的抗剪强度有重要影响,不应忽视。沈明荣等[7-8]用水泥砂浆制成的齿状节理试样进行了一系列直剪试验,讨论了节理剪切过程的扩容特性及峰值摩擦角应力效应。
鉴于天然岩石材料具有各向异性,而砂浆、石膏材料不能很好地代表天然岩石材料,且制作起来费工费时。而应用颗粒离散元软件PFC进行岩石试样直剪试验的模拟可以很好地避免上述问题,目前已经得到业内广泛认可,例如:宋英龙等[9]模拟不同接触状态节理试样的直剪试验,数值试验结果与室内物理试验吻合很好。Bahaaddini等[10]采用光滑节理模型模拟单齿节理的直剪试验,得到了节理凸起发生3种典型破坏的形态。曹日红等[11-13]从试样裂纹发育过程、节理壁岩性质差异和节理弱化等方面分析探讨了节理的剪切强度特征及破坏模式。
综上可知,现有研究主要考虑单一节理基础上几何形态、外法向应力以及剪切速率等因素对节理剪切强度、破坏特征等的影响规律。而自然界岩体中节理纵横交错,常常成组出现,例如共轭交错节理等。共轭节理相互交错形成菱形岩石夹块,其几何形态、发育和风化程度不同,力学性质相比单一节理要复杂得多。目前研究成果在复杂节理岩石剪切力学性质方面还很空缺,本文拟采用颗粒流软件PFC对含菱形夹块交错节理岩石的剪切力学性质进行初步分析,探讨节理剪裂角、外法向应力、节理摩擦性能等因素对试样剪切应力特征及破坏模式的影响规律,以期对深入研究复杂节理岩石力学性质提供借鉴参考。
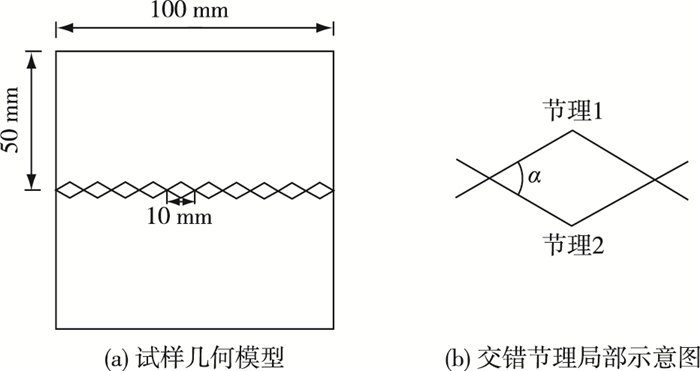
1 直剪试验模拟 1.1 试验方案岩石试样模型采用100 mm×100 mm的标准尺寸。菱形岩石夹块位于试样中间位置,由交错节理间歇接触生成,分布形式如图 1所示。定义夹块的小内角为剪裂角α,方案定为30°,40°,50°,60°,70°和80°共6种情形,上下节理的起伏角保持一致。
|
图 1 含交错节理岩石试样几何模型 Figure 1 Geometric model for rock sample having cross joint |
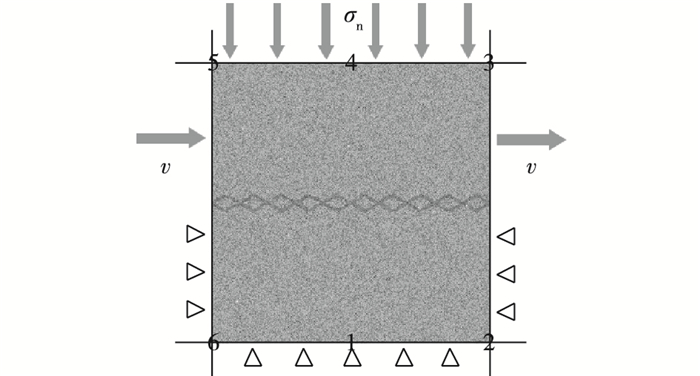
图 2中数值试验模型由上、下剪切盒组成;上剪切盒由3#,4#和5#墙组成;下剪切盒分别由1#,2#和6#墙组成。σn为试样顶部所施加的法向应力,通过给上剪切盒施加速度v来模拟剪切过程。试验中2#与6#墙的水平受力之和与剪切面积的比值为剪切应力,5#墙的水平位移为剪切位移。采用无围压单轴压缩试验对数值试样的力学参数进行标定,试样采用标准尺寸,高度h为100 mm,宽度b为50 mm,颗粒半径符合Rmax~Rmin的平均分布,Rmin=0.2 mm,Rmax=0.4 mm。颗粒间采用可以同时模拟颗粒间力和力矩的平行黏结模型[14],能够很好模拟岩石的力学性质。通过上加载板施加垂直向下的速度来实现加载,加载板纵向受力与试样表面积之比为轴向应力,加载板的轴向位移与试样高度之比为轴向应变。
|
图 2 直剪试验模型 Figure 2 Model for direct shear tests |
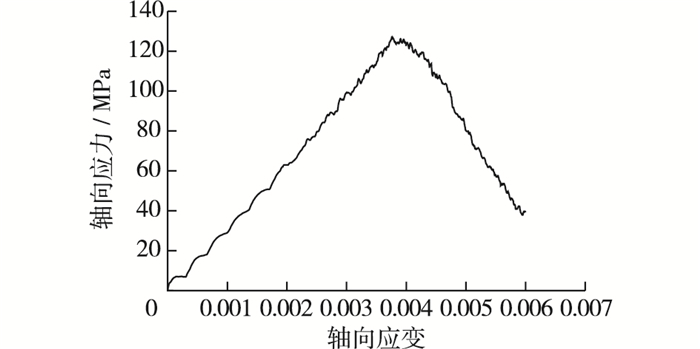
从图 3可知试样抗压强度σ为127.04 MPa,此时应变ε为0.003 76,可知弹性模量为33.79 GPa。数值试样的宏观力学参数比较合理,符合岩石属性的一般规律,细观参数见表 1。节理采用JSET命令设置起点、倾角和投影长度来实现,整条节理由20个小段来组成。采用去除黏结法[13]将节理处的细观参数设为0,以便更加真实地模拟凸起的挤压效应。
|
图 3 单轴压缩试验应力应变曲线 Figure 3 Stress-strain curve of uniaxial compression tests |
| 表 1 试样细观参数 Table 1 Sample mesoscopic parameters |
为研究节理岩石在恒定法向荷载边界条件下的循环剪切力学响应,首先采用Fish语言编写伺服函数,间接通过控制顶部墙体(图 1,4#)的加载速度来实现试样恒定法向荷载条件。剪切过程中每循环1次就会调用1次伺服函数,目的是降低4#墙上实际法向应力(σm)与目标法向应力(σr)之间的差值,使4#墙上实际法向应力保持基本恒定。4#墙上的实际加载速度为:
| $ {v^{(4)}} = G({\sigma _{\rm{m}}} - {\sigma _{\rm{r}}}) = G\mathit{\Delta }\sigma $ | (1) |
式中:G为伺服控制参数,其数值可由以下步骤计算得到。4#墙最大力增量为:
| $ \Delta {F^{(4)}} = k_{\rm{n}}^{(4)}{N_{\rm{c}}}{v^{(4)}}\mathit{\Delta }t $ | (2) |
式中:Nc为与4#墙接触的颗粒数;kn(4)为颗粒平均刚度;4#墙上的最大应力增量为力增量与墙面积A的比值,在本文中A等于试样宽度b。
| $ \mathit{\Delta }{\sigma ^{(4)}} = k_{\rm{n}}^{(4)}{N_{\rm{c}}}{v^{(4)}}\mathit{\Delta }t $ | (3) |
4#墙最大应力增量的绝对值应小于实测法向应力与目标法向应力差值的绝对值,这样可以保持剪切过程节理试样的整体稳定性,采用放松系数β(0~1)来实现,有:
| $ \mathit{|\Delta }{\sigma ^{(4)}}| < \beta |\mathit{\Delta }\sigma | $ | (4) |
将式(1)和(3)代入式(4)有:
| $ \frac{{k_{\rm{n}}^{(4)}{N_{\rm{c}}}G\left| {\mathit{\Delta }\sigma } \right|\mathit{\Delta }t}}{A} < \beta \left| {\mathit{\Delta }\sigma } \right| $ | (5) |
完成这个流程即可得到伺服控制参数G,将G代回式(1)便可以得到4#墙的实际加载速度,最终实现试样恒定法向荷载的施加。
| $ G = \frac{{\beta A}}{{k_{\rm{n}}^{(4)}{N_{\rm{c}}}\mathit{\Delta }t}} $ | (6) |
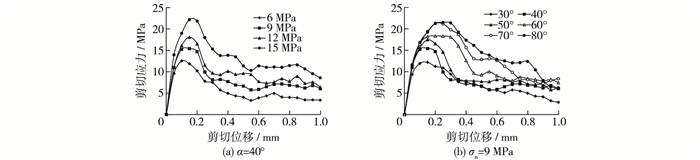
图 4为交错节理试样直剪试验具有代表性的剪切应力-剪切位移曲线,图 4(a)为剪裂角为40°不同法向应力的情形,图 4(b)为法向应力9 MPa时不同剪裂角的情形。曲线可以分为初始阶段、峰前阶段、峰后阶段和残余阶段。初始阶段,剪切应力快速增加,受剪裂角和法向应力的影响较小。峰前阶段,剪切应力增长速度均有所降低,夹块剪裂角和法向应力越大,剪切应力降低得越慢,因此剪应力峰值也越大。峰后阶段,剪应力快速下降后进入残余阶段,平均下降速度受剪裂角和法向应力的影响较小。残余阶段剪切应力大小与夹块剪裂角与法向应力大致保持正相关趋势。
|
图 4 剪切应力-剪切位移曲线 Figure 4 Shear stresses-shear displacement curves |
选取剪切应力峰值为剪切强度,表 2为岩石节理在不同法向应力下直剪试验的剪切强度。当法向应力从6 MPa增至15 MPa时,剪切强度在夹块剪裂角为30°~80°时分别增大了81.19%,82.07%,74.52%,68.24%,69.76%和64.36%,平均增加73.36%,增加量随起伏角的增加而降低。
| 表 2 剪切强度汇总 Table 2 Summary of shear strength |
当试样夹块剪裂角从30°增至80°时,剪切强度在法向应力为6~15 MPa时分别增加87.58%,72.38%,73.13%和70.14%,平均增加75.81%。将剪切强度与法向应力和夹块剪裂角数据绘制在直角坐标系中并进行线性拟合(见图 5),可以看出剪切强度随法向应力和夹块剪裂角的增大呈线性增加趋势,相关系数(R2)表明彼此的相关性很好。

|
图 5 剪切强度随影响因素变化曲线 Figure 5 Relationship curves of shear strength vs influencing factor |
定义剪切强度变化率k来反应交错节理与单一节理试样剪切强度的差异,其中τ0为单一节理试样的抗剪强度,τ1为交错节理试样的抗剪强度。
| $ k = ({\tau _1} - {\tau _0})/{\tau _0} $ | (7) |
表 3给出了各方案下剪切强度变化率k的汇总数据。各剪裂角方案下,剪切强度变化率k均为负值。节理试样剪切强度在法向应力为6,9,12和15 MPa时平均降低22.17%,17.38%,17.67%和15.46%,各应力下平均降低18.17%。结果表明交错节理试样较单一节理试样抵抗剪切应力的能力有明显下降。
| 表 3 剪切强度变化率 Table 3 Change rates of shear strength |
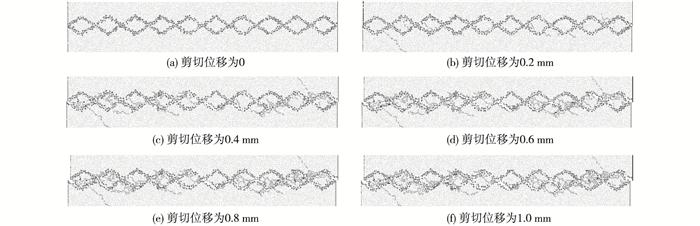
以试样夹块剪裂角为60°、法向应力12 MPa时为例,图 6给出了剪切过程试样局部裂纹扩展。黄色为节理面壁岩石,红色为节理,绿色为张拉裂纹,蓝色为剪切裂纹。当作用在颗粒之间的接触力大于切向黏结强度或法向黏结强度时,颗粒之间的接触就会发生破坏并产生裂纹。
|
图 6 剪切过程试样裂纹扩展(α=60°, σn=12 MPa) Figure 6 Crack propagation of jointed samples during shearing process (α=60°, σn=12 MPa) |
剪切开始时(图 6(a))试样内没有裂纹产生。剪切位移为0.2 mm时(图 6(b))试样内已有少量裂纹产生。随着剪切位移的增加(图 6(c)~(f)),试样内裂纹数持续增多,破坏规模加大。试样内裂纹主要在节理附近,表现为拉裂纹。中间夹块的破坏最为明显,裂纹发育形成的贯通面多位于夹块中部,随剪切位移的增大,破坏面逐渐演变为破坏带,与夹块表面切削破坏汇合。其次为下节理凸起,破坏凸起主要表现为根部剪断形式,剪切面随剪切位移的增加逐渐贯通。上节理凸起的破坏量最小,破坏凸起主要表现为表面切削破坏形式,破坏量随剪切位移增长变化不大。
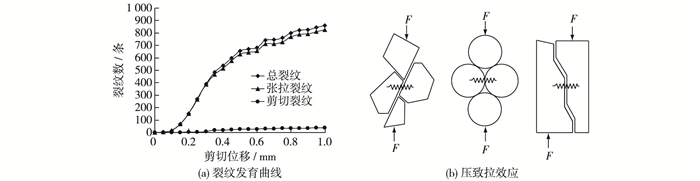
图 7(a)为岩石节理试样产生裂纹数随剪切过程的变化曲线,总裂纹数为张拉裂纹和剪切裂纹数目之和。量化的试样裂纹数变化规律与图 6所示规律一致。按照裂纹扩展速度可将曲线分为起裂阶段(剪切位移0~0.10 mm)、高速扩展阶段(剪切位移0.10~0.35 mm)和低速扩展阶段(剪切位移0.35~1.00 mm)。裂纹以张拉裂纹为主,表明试样颗粒间法向接触黏结的破坏占主导,表现为受拉破坏。节理凸起和中间夹块的相互挤压导致了颗粒间黏结发生张拉破坏,这种“压力致拉力”效应详见图 7(b)所示。
|
图 7 试样裂纹扩展规律及压致拉效应 Figure 7 Laws of crack propagation and compression induced tensile effect |
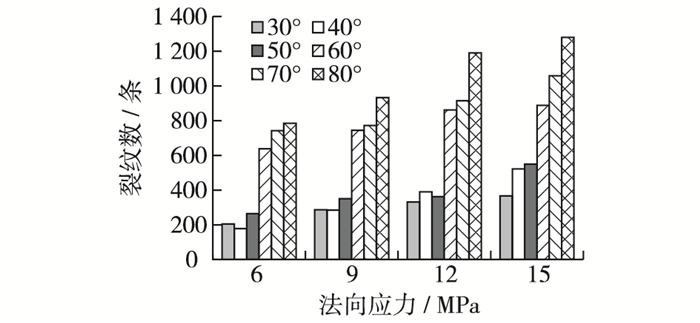
图 8为试样夹块不同剪裂角(30°,40°,50°,60°,70°和80°)时试样局部裂纹扩展,法向应力为9 MPa。可以看出试样裂纹均产生在中间夹块附近,均以张拉裂纹为主。随着夹块剪裂角的增大,节理凸起发生切削破坏逐渐加剧。在夹块剪裂角较大时(α=60°,70°和80°)部分凸起出现了根部剪断破坏,下节理凸起的破坏比上节理凸起更加明显。中间夹块的破坏主要有切削破坏、贯通破坏以及两者的组合破坏。随着夹块剪裂角的增加,夹块几何尺寸增大,3种破坏程度均有所增加。试样节理剪裂角越大,节理上下凸起与夹块之间的相互挤压、摩擦效应越明显,试样产生的破坏规模越大,在图 9中表现为裂纹数越多。另外从图 8中可以看出,相邻节理凸起与中间夹块两者之一发生较大幅度的破坏时,对另外一者的挤压效果会明显减弱,使其破坏幅度相应降低。

|
图 8 不同剪裂角试样局部裂纹扩展(σn=9 MPa) Figure 8 Crack propagation of specimens under different shear angles (σn=9 MPa) |
|
图 9 不同剪裂角时试样裂纹数对比 Figure 9 Comparison between number of specimen cracks |
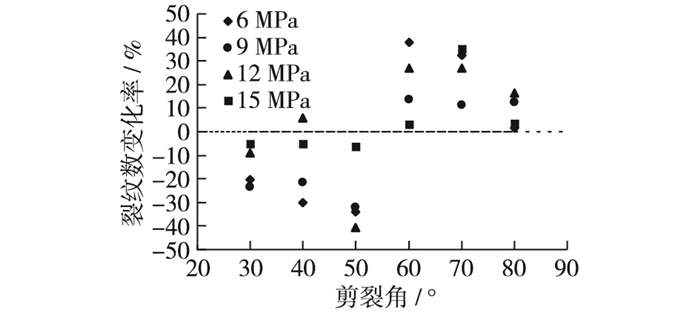
定义裂纹数变化率λ来反应交错节理与单一节理试样破坏规模的差异,其中n0为单一节理试样裂纹数,n1为交错节理试样裂纹数。
| $ \lambda = ({n_1} - {n_0})/{n_0} $ | (8) |
从图 10中可以看出,交错节理试样与相对应的单一节理试样破坏后产生的裂纹数差异很大。交错节理试样剪裂角在30°~50°时,与单一节理试样相比,其产生的裂纹数有减少趋势。交错节理试样剪裂角在60°~80°时,产生的裂纹数相比单一节理试样明显增加。这是因为,单一节理试样在不同粗糙条件下均发生不同程度的剪断破坏,而交错节理试样剪裂角较小时,主要以中间夹块破坏为主,因此裂纹数少于单一节理。剪裂角较大时,中间夹块破坏规模继续增大,上下节理夹层也发生了部分剪断破坏,因此裂纹数较单一节理试样有所增加。
|
图 10 交错节理试样与单一节理试样裂纹数对比 Figure 10 Comparison between crack numbers of interlaced in different shear angles joint specimen and single joint specimen |
节理间软弱夹层、渗流和风化等因素导致不同岩石节理间摩擦性能有明显差异,节理间摩擦性能对试样剪切性质的影响,通过改变表 1中所示的节理间摩擦系数f的数值来实现,考虑f分别为0,0.1,0.2,0.3,0.4和0.5的情形。方案仅改变节理处的摩擦系数,节理周围岩石内部的摩擦系数不发生变化。
4.1 剪应力增长规律图 11为试样夹块剪裂角为60°、法向应力为9 MPa时的剪切应力-剪切位移曲线。可以看出随着剪切位移的增加,节理间摩擦系数f对初始阶段剪应力的增长速率并无明显影响。峰前阶段,剪切应力增长速率相继出现明显降低,f越小,剪切应力降低得越快,对应的剪切应力峰值即剪切强度也就越小。峰后阶段,剪切应力开始降低,节理间f越小,降低速率越大,剪切应力进入残余阶段越早。
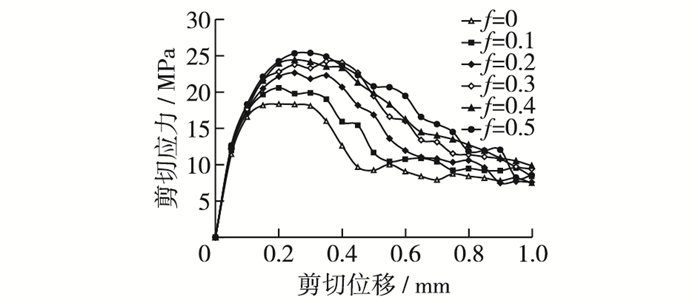
|
图 11 不同摩擦系数时剪切应力-剪切位移曲线 Figure 11 Shear stresses-shear displacement curves under different friction coefficients |
图 12为节理间摩擦系数与剪切强度的关系曲线,图 12(a)为夹块剪裂角为60°时不同法向应力的情形,图 12(b)为法向应力为9 MPa时不同剪裂角的情形。可以看出不同方案下,随着节理间f的增大,试样剪切强度整体均呈明显增加趋势。
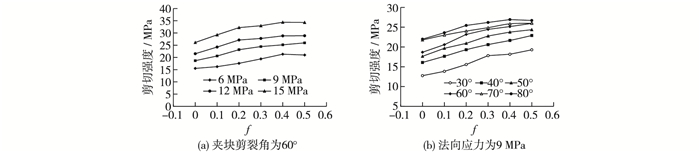
|
图 12 摩擦系数与剪切强度关系曲线 Figure 12 Relationship curves of friction coefficients and shear strength |
图 13为试样夹块剪裂角为60°、法向应力为9 MPa时的裂纹数-剪切位移曲线。起裂阶段裂纹增长速度几乎不受节理间摩擦系数的影响。高速扩展阶段和低速扩展阶段裂纹扩展速度受节理间摩擦系数的影响均较小。值得注意的是,节理间f越大,裂纹扩展曲线的高速扩展阶段越长,进入低速扩展阶段越晚,试样在高速扩展阶段产生的裂纹数明显增加。相应地,剪切结束时试样产生裂纹数也越多。
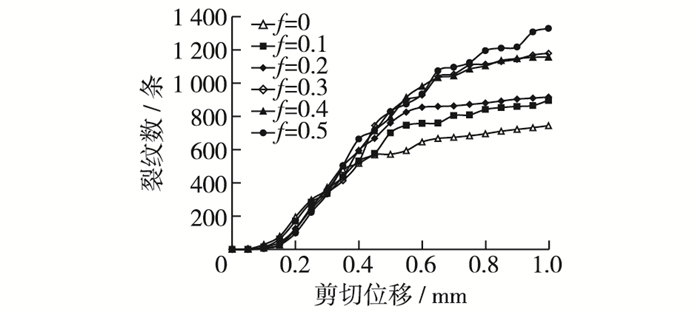
|
图 13 不同摩擦系数时裂纹数-剪切位移曲线 Figure 13 Crack number-shear displacement curves under different friction coefficients |
图 14给出了节理间摩擦系数不同时试样产生裂纹数对比情况,图 14(a)是基于夹块剪裂角为60°情形,图 14(b)是基于法向应力为9 MPa情形。从图 14可以看出节理间f不同,试样产生裂纹数呈现明显差异。节理间f为0~0.3时,试样裂纹数均随f的增加而增多。在f为0.3~0.5时,个别方案节理间f增加却导致试样裂纹数有少量减少。分析认为是由试样剪切破坏时裂纹扩展的随机性和复杂性所引起的。但整体上可以认为,随着节理间f的增加,节理凸起与中间夹块直剪的挤压效应加剧,因此试样产生裂纹数表现为增多趋势。
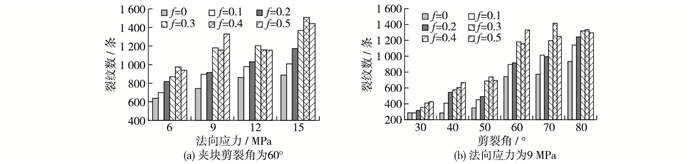
|
图 14 不同摩擦系数时试样裂纹数对比 Figure 14 Comparison between numbers of specimen cracks under different friction coefficients |
通过进行不同剪裂角交错节理岩石在不同法向应力下的直剪试验研究,得出以下主要结论:
(1) 剪切应力曲线分为初始阶段、峰前阶段、峰后阶段和残余阶段,其中峰前阶段剪切应力增长速率受法向应力和节理剪裂角的影响最大。剪切强度随法向应力与剪裂角的增加呈增大趋势。
(2) 剪切过程中试样破坏主要以节理凸起发生局部剪断破坏和中间夹块发生受压破坏为主,源于“压致拉”原理,产生裂纹主要以张拉裂纹为主。不同剪裂角节理试样的破坏随剪切角的增大而加剧,量化的裂纹数变化规律与裂纹扩展图保持一致。
(3) 交错节理岩石试样与单一节理试样相比,剪切强度有大幅降低,试样破坏规模在试样剪裂角较小(30°~50°)时显著缩小,在剪裂角较大(60°~80°)时则显著扩大。
(4) 节理间摩擦性能越强,剪切应力曲线峰前阶段剪切应力增长速度越大,裂纹扩展曲线高速扩展阶段越长,进入低速扩展阶段越晚,抗剪强度越大。摩擦性能的增加导致节理局部挤压、摩擦效应大大提高,试样破坏规模明显扩大。
| [1] |
BARTON N, CHOUBEY V. The shear strength of rock joints in theory and practice[J]. Rock Mechanics, 1977, 10(1/2): 1-54. |
| [2] |
BARTON N, BANDIS S. Effects of block size on the shear behavior of jointed rock[C]//Proceedings of the 23rd U. S. Symposium on Rock Mechanics. Berkeley: [s. n. ], 1982: 739-760. http://ci.nii.ac.jp/naid/10016742429
|
| [3] |
赵坚. 岩石节理剪切强度的JRC-JMC新模型[J]. 岩石力学与工程学报, 1998, 17(4): 349-357. ( ZHAO Jian. A new JRC-JMC shear strength criterion for rock joint[J]. Chinese Journal of Rock Mechanics and Engineering, 1998, 17(4): 349-357. (in Chinese)) |
| [4] |
李海波, 冯海鹏, 刘博. 不同剪切速率下岩石节理的强度特性研究[J]. 岩石力学与工程学报, 2006, 25(12): 2435-2440. ( LI Haibo, FENG Haipeng, LIU Bo. Study on strength behavior of rock joints under different shearing velocities[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(12): 2435-2440. DOI:10.3321/j.issn:1000-6915.2006.12.008 (in Chinese)) |
| [5] |
王刚, 张学朋, 蒋宇静, 等. 一种考虑剪切速率的粗糙结构面剪切强度准则[J]. 岩土工程学报, 2015, 37(8): 1399-1404. ( WANG Gang, ZHANG Xuepeng, JIANG Yujing, et al. New shear strength criterion for rough rock joints considering shear velocity[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(8): 1399-1404. (in Chinese)) |
| [6] |
朱小明, 李海波, 刘博, 等. 含一阶和二阶起伏体节理剪切强度的试验研究[J]. 岩石力学与工程学报, 2011, 30(9): 1810-1818. ( ZHU Xiaoming, LI Haibo, LIU Bo, et al. Experimental study of shear strength of joints with first-order and second-order asperities[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(9): 1810-1818. (in Chinese)) |
| [7] |
沈明荣, 张清照. 规则齿型结构面剪切特性的模型试验研究[J]. 岩石力学与工程学报, 2010, 29(4): 713-719. ( SHEN Mingrong, ZHANG Qingzhao. Experimental study of shear deformation characteristics of rock mass discontinuities[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(4): 713-719. (in Chinese)) |
| [8] |
罗战友, 杜时贵, 黄曼. 岩石结构面峰值摩擦角应力效应试验研究[J]. 岩石力学与工程学报, 2014, 33(6): 1142-1148. ( LUO Zhanyou, DU Shigui, HUANG Man. Experimental study of stress effect on peak friction angle of rock structural plane[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(6): 1142-1148. (in Chinese)) |
| [9] |
宋英龙, 夏才初, 唐志成, 等. 不同接触状态下粗糙节理剪切强度性质的颗粒流数值模拟和试验验证[J]. 岩石力学与工程学报, 2013, 32(10): 2028-2035. ( SONG Yinglong, XIA Caichu, TANG Zhicheng, et al. Numerical simulation and test validation for direct shear properties of rough joints under different contact states[J]. Chinese Journal of Rock Mechanics and Engineering, 2013, 32(10): 2028-2035. (in Chinese)) |
| [10] |
BAHAADDINI M, SHARROCK G, HEBBLEWHITE B K. Numerical direct shear tests to model the shear behavior of rock joints[J]. Computers & Geotechnics, 2013, 51(13): 101-115. |
| [11] |
曹日红, 曹平, 林杭, 等. 不同粗糙度的节理直剪颗粒流分析[J]. 岩土力学, 2013, 34(增刊2): 456-463. ( CAO Rihong, CAO Ping, LIN Hang, et al. Particle flow analysis of direct shear tests on joints with different roughnesses[J]. Rock and Soil Mechanics, 2013, 34(Suppl2): 456-463. (in Chinese)) |
| [12] |
张雅慧, 汪丁建, 唐辉明, 等. 基于PFC2D数值试验的异性结构面剪切强度特性研究[J]. 岩土力学, 2016, 37(4): 1031-1041. ( ZHANG Yahui, WANG Dingjian, TANG Huiming, et al. Study of shear strength characteristics of heterogeneous discontinuities using PFC2D simulation[J]. Rock and Soil Mechanics, 2016, 37(4): 1031-1041. (in Chinese)) |
| [13] |
余华中, 阮怀宁, 褚卫江. 弱化节理剪切力学特征的颗粒流模拟研究[J]. 岩土力学, 2016, 37(9): 2712-2720. ( YU Huazhong, RUAN Huaining, CHU Weijiang. Particle flow modeling of shear characteristic of weakened joint[J]. Rock and Soil Mechanics, 2016, 37(9): 2712-2720. (in Chinese)) |
| [14] |
Itasca Consulting Group Inc. PFC2D(particle flow code in 2D) theory and background[R]. Minnesota, USA: Itasca Consulting Group.
|
 2018
2018 