岩石是由矿物或岩屑在地质作用下按一定规律聚集形成的自然集合体, 其内部存在一定的微缺陷[1]。在外荷载的作用下, 岩石内部会出现新的裂纹和孔洞, 当发生扩展和贯通时, 岩石内部积蓄的大量弹性能瞬间释放, 导致岩体失稳破坏, 岩石受力变形破坏过程中能量耗散与能量释放是引发岩石损伤和破坏的内在原因。因此, 研究岩石的强度变形特征以及能量耗散规律, 对研究岩石内在的破坏机理和工程岩体开挖的稳定性具有重大意义。
近年来, 许多研究人员对岩石破坏过程中的强度变形特征以及能量耗散规律进行了试验研究, Xie等[2]通过对含天然裂缝的大理岩进行大量的单轴压缩试验, 考察了其力学性能并与完整岩石进行对比, 认为破裂大理岩的破坏是一个局部渐进的过程; Zong等[3]通过对砂岩进行大量的三轴压缩试验, 研究了砂岩的力学性质和损伤演化特性, 并分析了砂岩在不同应力状态下的应力应变曲线特征和变形强度特性; Deng等[4]基于分形岩石力学和断裂力学理论, 提出了一种新的岩石破碎过程能耗模型; 周辉等[5]对花岗岩进行三轴压缩试验, 分析了不同围压下花岗岩断口的微观形貌特征, 并讨论了花岗岩的脆性破坏机制; 付建新等[6]对闪长玢岩进行三轴加卸载的岩石力学试验, 分析了复杂应力路径下脆性岩石的力学及破裂特征; 陈景涛[7]对花岗岩进行常规三轴压缩试验, 探讨了围压对岩石变形特征的影响; 苏承东等[8]对煤样进行常规三轴压缩试验, 分析了煤样在不同应力条件下的强度和变形特征; 张亚鹏等[9]通过对砂岩进行单轴和三轴压缩试验, 定量分析了围压对岩石强度和变形特性的影响, 并根据Mohr-Coulomb准则得到相应的岩石强度参数; 李地元等[10]通过开展大量花岗岩的三轴加卸载试验, 分析了花岗岩在不同路径下的变形破坏及强度特征, 并给出了相关准则中的参数; 谢和平等[11]讨论了岩石变形破坏中能量耗散、释放与岩石强度和整体破坏的内在联系; 陈子全等[12]通过开展砂岩单轴压缩、常规三轴以及卸荷三轴试验, 研究了砂岩在不同应力路径下的能耗规律; 杨圣奇等[13]基于大理岩的常规三轴压缩试验, 探究了围压对岩石变形破坏和能量特征的影响规律; 许国安等[14]对砂岩进行单轴和三轴压缩试验, 对比分析了砂岩在加卸载条件下的能耗特征; 于水生等[15]通过对花岗岩进行三轴压缩试验, 分析了其能量特征与应力、应变及围压之间的关系; 田勇等[16]通过对灰岩岩样进行三轴压缩试验, 得到了峰值应力和弹性模量与围压的线性关系式, 并分析了岩样压缩过程中几个阶段的能量转化方式。
综上, 尽管目前在岩石强度变形特性方面取得了不少成果, 但在岩石破坏过程中能量耗散规律方面研究较少。本文拟通过对华山花岗岩开展单轴和常规三轴试验, 比较不同围压下应力应变曲线形状特征, 分析扩容阈值、峰值应变、弹性模量等与围压的关系, 探讨岩石破坏过程中的能量耗散规律及其与围压的相关特性。
1 试验原理与过程试验在MTS815电液伺服岩石力学三轴试验机上完成, 三轴试验中围压分别设置为15, 25和35 MPa。试验机的最大轴压为1 700 kN, 最大围压可达45 MPa, 围压加载速率为0.2 MPa/s, 轴向加载采用应力和位移共同控制。在试验初期采用应力控制, 加载速率为1.0 kN/s; 接近峰值强度时采用位移控制, 位移加载速率为0.02 mm/min; 最后加载直至使试件失去承载能力而破坏。花岗岩石材取自陕西省华山地区, 呈灰白色, 属于中细粒黑云母花岗岩。该花岗岩的平均密度为2 600 kg/m3, 吸水率为0.57%。其矿物成分主要有微斜长石(41%)、斜长石(27%)、石英(22%)和黑云母(7%)等。
试样尺寸为Φ50×100 mm, 经钻芯、切割等加工而成(见图 1), 其端面不平行度控制在0.05 mm以内。对自然状态下的试样进行波速密度测试, 纵波波速为3 846~4 255 m/s。每组围压(0, 15, 25和35 MPa)各选取3个试样进行试验, 各组试样的波速如表 1所示, 最后得到的力学参数为试验数据的平均值。

|
图 1 花岗岩试样照片 Figure 1 Photo of granite samples |
| 表 1 不同围压下试样分组的波速 Table 1 Wave velocity of specimens under different confining pressures |
由于岩石内部存在微缺陷(如孔洞和裂纹), 故在加载初始阶段, 岩石被逐渐压密, 使得偏应力-轴向应变曲线出现上凹现象(图 2), 随着围压的增加, 上凹现象减弱, 这是由于围压限制了微缺陷被压密的速度。峰值强度随围压的增大近似呈线性增大; 达到峰值强度后, 轴向应力应变曲线跌落明显, 表明在所研究的围压范围内花岗岩表现出明显的脆性特征。特别在35 MPa围压情况下岩样的应力应变曲线在达到峰值应力时跌落了一段距离, 此时岩石发生局部破坏, 但岩石仍具有较大的承载力, 然后, 应力应变曲线又开始发生跌落, 岩石发生整体破坏。
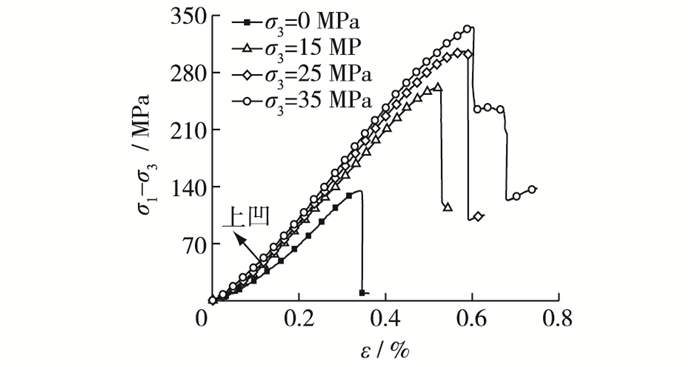
|
图 2 偏应力-轴向应变曲线 Figure 2 Curves of deviatoric stress and axial strain |
图 3是不同围压下花岗岩试样的偏应力-径向应变曲线。可见, 在单轴压缩条件下, 试样达到峰值强度时, 最大径向变形为0.24%, 当围压提高到25 MPa时, 径向变形增加至0.71%, 当围压提高到35 MPa时, 最大径向变形减小至0.67%, 可见岩样径向变形先增大后减小, 这与文献[17]中结论一致。
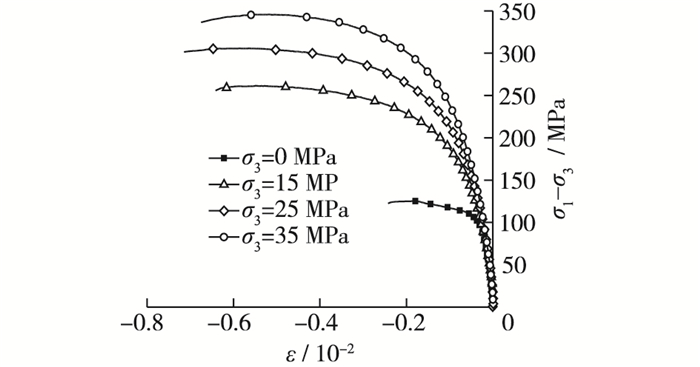
|
图 3 偏应力-径向应变曲线 Figure 3 Curves of deviatoric stress and radial strain |
在常规压缩试验中, 花岗岩弹性模量与围压的关系及花岗岩峰值应变与围压的关系如图 4。可见, 围压使试样内部的孔洞和裂纹发生闭合, 改善了颗粒间的摩擦力, 从而提高了试样的力学性能, 故弹性模量随围压增大而增大。单轴下花岗岩的弹性模量为45.94 GPa, 15 MPa下的弹性模量为58.86 GPa, 相比单轴增加了12.92 GPa; 25 MPa下弹模为62.86 GPa, 相比15 MPa下增加了4 GPa; 35 MPa下弹性模量为66.08 GPa, 相比25 MPa增加3.22 GPa, 说明围压对弹性模量的增强作用随围压增加而逐渐减小。图 4表明花岗岩试样的峰值应变随着围压的增大而增大, 单轴下峰值应变为0.34%, 在15 MPa下峰值应变为0.52%, 25 MPa下峰值应变为0.60%, 35 MPa下峰值应变为0.60%, 反映出围压对岩石峰值应变的增强作用逐渐降低, 这是由于围压的提高, 对试样侧向变形抑制作用逐渐加强, 试样内部的微缺陷逐渐被压密, 导致峰值应变增加缓慢。

|
图 4 弹性模量与围压及峰值应变与围压的关系 Figure 4 Relationship of elastic modulus with confining pressure and relationship of peak strain with confining pressure |
花岗岩在单调压缩过程中的偏应力与体应变曲线如图 5所示, 可知在单轴和三轴压缩条件下花岗岩的体应变在荷载较小时都表现出线性变化, 且岩样的体积随荷载的增大而减小。当外荷载达到一定值后, 体积应变曲线出现反弯, 开始发生体积膨胀, 即产生扩容现象。这是因为试件内部微裂纹的张开、扩展与贯通, 导致岩石内孔隙裂隙等不断增大的结果。图 5中的σcd表示岩石发生扩容时对应的轴向应力, 即扩容阈值。此外, 可看出随着围压增加, 岩样的扩容阈值随之增加, 这是由于围压对岩样侧向变形具有一定的抑制作用, 从而降低了裂纹扩展的速度, 推迟了岩石扩容现象发生。图 6显示一定围压范围内, 此岩石的扩容阈值与围压近似呈线性关系, 可见围压影响岩石的扩容特性。
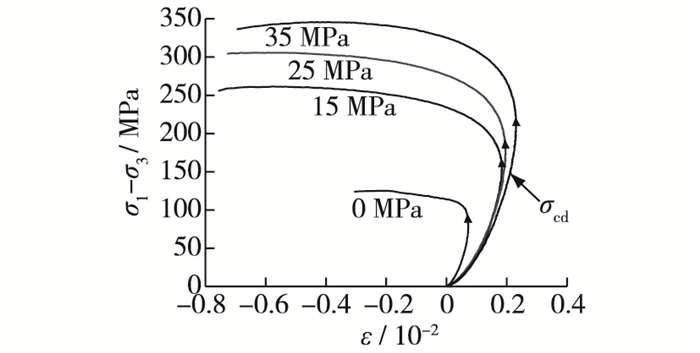
|
图 5 偏应力-体应变曲线 Figure 5 Curves of deviatoric stress and volumetric strain |
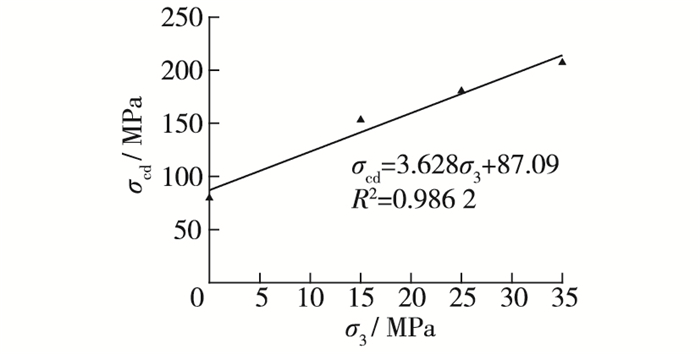
|
图 6 扩容阈值与围压关系 Figure 6 Relationship of dilatation threshold with confining pressures |
图 7为单轴和三轴(35 MPa)压缩试验后岩样破坏形态对比, 可以发现单轴压缩下岩样表面出现多处纵向裂隙, 局部有小片状剥落, 属典型的柱状劈裂破坏, 而三轴压缩下的岩样表面出现了1条斜裂缝, 并贯穿整个岩样, 呈现出明显的压剪破坏, 可见围压改变了岩样的破坏形式。在围压较低时, 岩石主要的破坏模式为劈裂拉伸破坏, 未见明显的剪切面; 随着围压的提高, 岩石的破坏模式逐渐从劈裂破坏向剪切破坏过渡。

|
图 7 单轴和三轴压缩下岩样破坏形态 Figure 7 Failure patterns of specimens under uniaxial and triaxial compressions |
Mohr-Coulomb准则[18]是岩石力学中广泛应用的强度准则之一, 能较好地揭示岩石压缩过程中发生剪切破坏的机理, 相应的表达式如下:
| $ \tau = \sigma {\rm{tan}}\varphi + c $ | (1) |
式中:τ为剪切面上的最大主应力; σ为剪切面上的正应力; c, φ分别为岩石的黏聚力和内摩擦角。
由式(1)可知, 岩石的抗剪强度与中间主应力无关, 因此可以建立最大主应力和最小主应力之间的关系, 故而可以建立如下关系式:
| $ {\sigma _1} = a + b{\sigma _3} $ | (2) |
式中:a, b为岩石强度参数, a=2ccosφ/(1-sinφ), b=(1+sinφ)/(1-sinφ)。
参数a, b实际上为图 8中拟合直线在纵坐标轴上的截距和拟合直线的斜率。
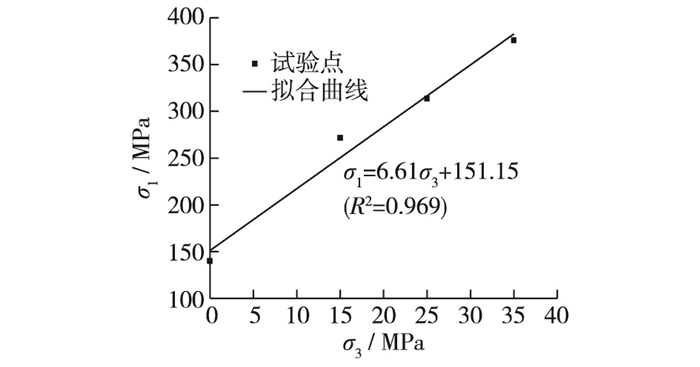
|
图 8 Mohr-Coulomb强度准则拟合曲线 Figure 8 Fitting curve by Mohr-Coulomb strength criterion |
通过计算得相应岩石参数为:a=151.15 MPa, b=6.61, c=47.49 MPa, φ=29.40°, R=0.984。可见拟合效果较好, 由此可得到此花岗岩的Mohr-Coulomb准则强度包络线如下:
| $ \tau = \sigma {\rm{tan}}29.4^\circ + 47.49 $ | (3) |
考虑单位体积岩石单元在外荷载作用下产生变形, 假设该物理过程中没有热交换, 外力功所产生的总输入能量为U, U可近似等于单位体积岩样实际吸收的能量U0(即吸收能密度, 下简称为吸收能), 根据热力学第一定律:
| $ U = {U_0} = {U^{\rm{d}}} + {U^{\rm{e}}} $ | (4) |
式中:Ud为耗散能密度(下简称为耗散能), 用于形成单元内部损伤和塑性变形, 即耗散于岩体内裂纹的萌生和扩展; Ue为可释放的弹性应变能密度(下简称为弹性应变能), 该部分能量形成于岩体单元发生弹性应变阶段, 当外力卸除时, 这部分能量能使岩体变形得到一定的恢复; U0, Ue和Ud的单位均为MJ/m3, 与应力单位MPa等同。
许国安等[14]经过推导(过程略), 给出了单轴和传统三轴压缩下吸收能计算公式分别如下:
| $ {U_0} = \smallint {\sigma _1}{\rm{d}}{\varepsilon _1} $ | (5) |
| $ {U_0} = \smallint {\sigma _1}{\rm{d}}{\varepsilon _1} + 2\smallint {\sigma _3}{\rm{d}}{\varepsilon _3} $ | (6) |
弹性应变能计算式如下:
| $ {U^{\rm{e}}} = \sigma _1^2/\left( {2E} \right) $ | (7) |
式中:σ1为轴向应力; E为弹性模量(峰前弹性段斜率); ε1和ε3分别为岩样的轴向和径向应变。
式(4)经过变换可得耗散能的计算式如下:
| $ {U^{\rm{d}}} = {U_0}-{U^{\rm{e}}} $ | (8) |
| $ {由岩样的泊松比效应可知: }\mu =-\frac{{{\varepsilon _3}}}{{{\varepsilon _1}}} $ | (9) |
由式(6)和(9)可得到三轴下岩样实际的吸收能为:
| $ {U_0} = \smallint ({\sigma _1}-2\mu {\sigma _3}){\rm{d}}{\varepsilon _1} $ | (10) |
图 9为岩石破坏前(轴向应力达到峰值时)吸收能与应变的关系曲线, 对每一种围压下的10组数据进行拟合, 发现满足拟合公式Y=αX2+βX+γ(Y是吸收能, X是轴向应变, α, β和γ是拟合系数), 具体见表 2所示, 拟合相关系数在0.99以上。从图 9可知, 吸收能随着轴向应变的增大而增大, 在相同轴向应变下, 围压越大岩石吸收的能量越多。
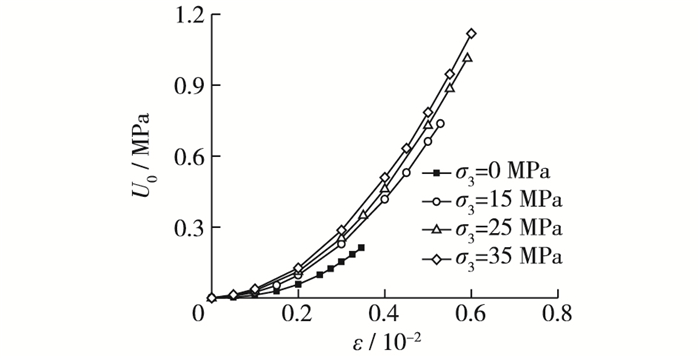
|
图 9 不同围压下吸收能与应变关系 Figure 9 Relationship between absorbed energy and strain under different confining pressures |
| 表 2 不同围压下吸收能与应变的拟合参数 Table 2 Fitting parameters of absorbed energy- strain under different confining pressures |
图 10为不同围压下岩石破坏过程的能量变化关系曲线, 可见在单轴和三轴压缩条件下:①加载初始阶段OA, 加载曲线的斜率较小, 岩石处于压密状态, 岩石吸收的能量较少, 耗散能略大于弹性应变能, 此时外力做的功主要耗散在岩石原有微裂纹的压密和内部颗粒发生咬合用来克服摩擦力, 一小部分能量以弹性应变能的形式储存起来; ②线弹性段AB, 弹性应变能曲线与吸收能曲线基本保持平行发展并呈线性增加, 耗散能缓慢增加, 而弹性应变能快速增加, 线弹性阶段是岩样主要储能阶段; ③破裂稳定发展阶段BC, 加载曲线斜率开始变小, 随着新裂纹的萌生和已有裂纹的稳定扩展, 耗散能开始增加, 弹性应变能的增加速度开始变缓; ④破裂不稳定发展阶段CD, 岩石内部的微裂纹出现不稳定扩展并发生贯通, 耗散能增速加快, 弹性应变能增速大幅度降低, 但此时弹性应变能仍占主导地位, 并在峰值点D处达到最大值; ⑤应力跌落段DE, 加载曲线急剧跌落, 岩样内部微裂纹汇聚成主裂缝, 导致其发生整体破坏, 岩样内部积蓄的弹性应变能瞬间释放, 耗散能急剧增加。
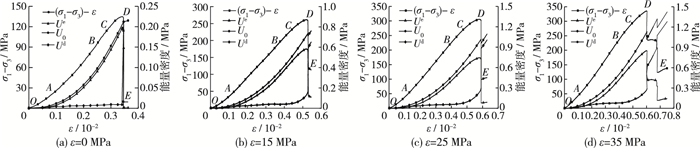
|
图 10 不同围压下岩石破坏过程偏应力-能量-应变曲线 Figure 10 Deviatoric stress-energy-strain curves under different confining pressures |
三轴压缩条件下由于围压的存在, 应力应变曲线在岩样破坏后并未完全跌落, 岩样内部储存的弹性应变能并不会像单轴压缩时瞬间几乎全部转化为耗散能, 而是逐渐耗散于岩石微宏观的裂纹扩展中, 直到岩样发生整体破坏, 这表明三轴压缩下岩石的失稳破坏是能量逐渐释放的过程, 所以耗散能曲线的变化可反映岩石内部损伤和破裂的产生情况。此外, 相比于单轴压缩, 在三轴压缩下岩样吸收能量在达到峰值点后存在短暂降低的现象, 这主要是因为岩样在峰值点破坏时, 轴向应变基本不变, 而径向应变陡增, 即轴向应力基本不做功, 岩样膨胀对液压油做的负功占据主导作用。另外, 由于围压的限制作用, 在岩样破坏的残余变形阶段, 内部仍储存了一部分能量, 但相比于耗散能则微乎其微, 此时岩样吸收的能量大部分都转化为耗散能, 主要耗散于岩样的剪切滑移中。
3.2 围压对能量演化的影响由图 11可知, 三轴压缩下岩石破坏时吸收能和耗散能都远大于单轴压缩, 并随着围压的增大而增大, 且均与围压存在良好的线性关系。在围压15, 25与35 MPa下, 试样破坏时吸收能分别为单轴的3.31, 4.45和5.54倍, 而耗散能分别为单轴的2.49, 4.14和5.07倍, 主要是因为在三轴压缩时, 由于围压的约束作用, 增大了微破裂面上颗粒间的咬合摩擦力, 在与单轴压缩产生相同程度的损伤时, 岩样在三轴压缩下则需要吸收和耗散更多的能量。

|
图 11 吸收能及耗散能与围压的关系 Figure 11 Relationship of absorbed energy and dissipated energy with confining pressure |
对于弹性应变能而言, 当应力达到峰值强度时, 储存在岩石内的能量达到最大值, 其峰值点称为岩石的储能极限(Umaxe)[19], 储能极限与围压的关系如图 12所示, 可知岩石的储能极限随着围压的增大而增大, 并与围压存在较好的线性关系。
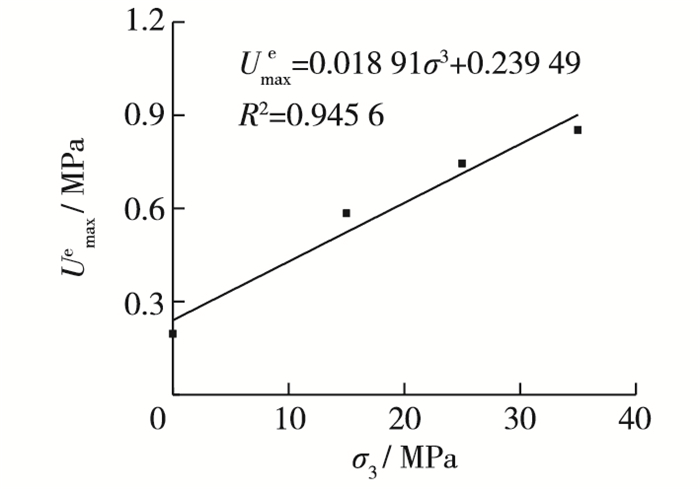
|
图 12 储能极限与围压间关系 Figure 12 Relationship between energy-storage limit and confining pressure |
本文对华山花岗岩开展单轴和常规三轴压缩试验, 分析了其应力应变行为、强度与变形特征以及能量耗散规律, 得到以下主要结论:
(1) 华山花岗岩表现出明显的脆性特征, 在三轴压缩条件下应力应变曲线的上凹现象相比于单轴变得不明显; 随着围压的增加, 花岗岩的弹性模量和峰值应变不断增大, 但增长率逐渐变慢; 花岗岩的扩容阈值与围压近似呈线性增加关系。
(2) 在单轴压缩条件下, 岩样外表面可见很多纵向分布的拉伸裂纹, 局部有片状剥落, 柱状劈裂破坏的特征明显, 岩样内部储存的弹性应变能在峰值后几乎瞬间都转化为耗散能, 呈现出突发性的破坏特征。
(3) 三轴压缩下, 岩样呈现出剪切破坏模式, 其吸收能、弹性应变能以及耗散能都远大于单轴压缩情形下对应值, 并且随着围压的增大而增大。岩样储能极限值与施加的围压存在着良好的线性关系。
| [1] |
沈明荣, 陈建峰. 岩体力学[M]. 上海: 同济大学出版社, 2006. ( SHEN Mingrong, CHEN Jianfeng. Rockmass mechanics[M]. Shanghai: Tongji University Press, 2006. (in Chinese))
|
| [2] |
XIE H, PEI J, ZUO J, et al. Investigation of mechanical properties of fractured marbles by uniaxial compression tests[J]. Journal of Rock Mechanics and Geotechnical Engineering, 2011, 3(4): 302-313. DOI:10.3724/SP.J.1235.2011.00302 |
| [3] |
ZONG Y, HAN L, WEI J, et al. Mechanical and damage evolution properties of sandstone under triaxial compression[J]. International Journal of Mining Science and Technology, 2016, 26(4): 601-607. DOI:10.1016/j.ijmst.2016.05.011 |
| [4] |
DENG Y, CHEN M, JIN Y, et al. Theoretical analysis and experimental research on the energy dissipation of rock crushing based on fractal theory[J]. Journal of Natural Gas Science and Engineering, 1998, 90: 231-239. |
| [5] |
周辉, 孟凡震, 刘海涛, 等. 花岗岩脆性破坏特征与机制试验研究[J]. 岩石力学与工程学报, 2014, 33(9): 1822-1827. ( ZHOU Hui, MENG Fanzheng, LIU Haitao, et al. Experimental study on characteristics and mechanism of brittle failure brittle of granite[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1822-1827. (in Chinese)) |
| [6] |
付建新, 宋卫东, 谭玉叶. 复杂加卸载路径下闪长玢岩强度特征及声发射特性试验研究[J]. 岩石力学与工程学报, 2016, 35(增刊2): 3858-3867. ( FU Jianxin, SONG Weidong, TAN Yuye. Experimental study of the characteristics of strength and AE of Driorite porphyrite under complex loading and unloading path[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl2): 3858-3867. (in Chinese)) |
| [7] |
陈景涛. 岩石变形特征和声发射特征的三轴试验研究[J]. 武汉理工大学学报, 2008, 30(2): 94-96, 118. ( CHEN Jingtao. Experimental study on triaxial compression deformation and acoustic emission property of rock[J]. Journal of Wuhan University of Technology, 2008, 30(2): 94-96, 118. (in Chinese)) |
| [8] |
苏承东, 翟新献, 李永明, 等. 煤样三轴压缩下变形和强度分析[J]. 岩石力学与工程学报, 2006, 25(增刊1): 2963-2968. ( SU Chengdong, ZHAI Xinxian, LI Yongming, et al. Study on deformation and strength of coal samples in triaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Suppl1): 2963-2968. (in Chinese)) |
| [9] |
张亚鹏, 韩杨, 白哲, 等. 砂岩单轴和三轴压缩试验力学效应分析[J]. 河南城建学院学报, 2016, 25(6): 16-20. ( ZHANG Yapeng, HAN Yang, BAI Zhe, et al. Experimental analysis on mechanical effects of sandstone under uniaxial and triaxial compression tests[J]. Journal of Henan University of Urban Construction, 2016, 25(6): 16-20. (in Chinese)) |
| [10] |
李地元, 孙志, 李夕兵, 等. 不同应力路径下花岗岩三轴加卸载力学响应及其破坏特征[J]. 岩石力学与工程学报, 2016, 35(增刊2): 3449-3457. ( LI Diyuan, SUN Zhi, LI Xibing, et al. Mechanical response and failure characteristics of granite under different stress paths in triaxial loading and unloading conditions[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl2): 3449-3457. (in Chinese)) |
| [11] |
谢和平, 鞠杨, 黎立云. 基于能量耗散与释放原理的岩石强度与整体破坏准则[J]. 岩石力学与工程学报, 2005, 24(17): 3003-3010. ( XIE Heping, JU Yang, LI Liyun. Criteria for strength and structural failure of rocks based on energy dissipation and energy release principles[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(17): 3003-3010. DOI:10.3321/j.issn:1000-6915.2005.17.001 (in Chinese)) |
| [12] |
陈子全, 李天斌, 陈国庆, 等. 不同应力路径下砂岩能耗变化规律试验研究[J]. 工程力学, 2016, 33(6): 120-128. ( CHEN Ziquan, LI Tianbing, CHEN Guoqing, et al. Experimental study on energy evolution of sandstone under different stress paths[J]. Engineering Mechanics, 2016, 33(6): 120-128. (in Chinese)) |
| [13] |
杨圣奇, 徐卫亚, 苏承东. 大理岩三轴压缩变形破坏与能量特征研究[J]. 工程力学, 2007, 24(1): 136-142. ( YANG Shengqi, XU Weiya, SU Chengdong. Study on the deformation failure and energy properties of marble specimen under triaxial compression[J]. Engineering Mechanics, 2007, 24(1): 136-142. (in Chinese)) |
| [14] |
许国安, 牛双建, 靖洪文, 等. 砂岩加卸载条件下能耗特征试验研究[J]. 岩土力学, 2011, 32(12): 3611-3617. ( XU Guoan, LIU Shuangjian, JING Hongwen, et al. Experimental study of energy features of sandstone under loading and unloading[J]. Rock and Soil Mechanics, 2011, 32(12): 3611-3617. DOI:10.3969/j.issn.1000-7598.2011.12.013 (in Chinese)) |
| [15] |
于水生, 卢玉斌, 蔡勇. 三轴压缩下花岗岩能量特性研究[J]. 应用数学和力学, 2015, 36(增刊1): 147-154. ( YU Shuisheng, LU Yubin, CAI Yong. Study on the energy properties of granite under triaxial compression loading[J]. Applied Mathematics and Mechanics, 2015, 36(Suppll): 147-154. (in Chinese)) |
| [16] |
田勇, 俞然刚. 不同围压下灰岩三轴压缩过程能量分析[J]. 岩土力学, 2014, 35(1): 118-122, 129. ( TIAN Yong, YU Rangang. Energy analysis of limestone during triaxial compression under different confining pressures[J]. Rock and Soil Mechanics, 2014, 35(1): 118-122, 129. (in Chinese)) |
| [17] |
徐荃. 花岗岩峰后变形特点与脆性关系研究[D]. 沈阳: 东北大学, 2014. (XU Quan. Research about post-peak deformation features and brittleness index of granite[D]. Shenyang: Northeastern University, 2014. (in Chinese))
|
| [18] |
LABUZ J F, ZANG A. Mohr-Coulomb failure criterion[J]. Rock Mechanics and Rock Engineering, 2012, 45(6): 975-979. DOI:10.1007/s00603-012-0281-7 |
| [19] |
张志镇, 高峰. 受载岩石能量演化的围压效应研究[J]. 岩石力学与工程学报, 2015, 34(1): 1-11. ( ZHANG Zhizhen, GAO Feng. Confining pressure effect on rock energy[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(1): 1-11. (in Chinese)) |
 2018
2018 
