海上筒型基础是一种适用于软土地基的港口与海岸工程结构, 其基础结构一般为沉入软土地基的无底空心圆筒, 现已广泛应用于海上防波堤、海上风电、海上栈桥等工程的基础设计中, 在实际应用中已取得初步成功。筒型基础主要由作用于基础筒上的土压力和基础筒体与地基土体的摩擦保持稳定, 故基础筒上的土压力是影响其结构稳定的关键因素。
目前筒型基础筒壁土压力的计算尚无合适规范, 其研究方法主要以有限元分析为主, 王元战等[1]建立了四筒基础防波堤的三维有限元模型, 分析了不同波浪荷载作用下筒壁土压力在竖向和环向的分布规律, 结合结构的不同位移模式, 给出了不同区域土压力的简化计算方法。蒋敏敏等[2]建立箱筒基础防波堤的二维平面应变模型, 分析了筒体内外不同位置处土压力分布的一般规律。蔡正银等[3]通过对新型桶式基础防波堤进行三维有限元建模, 分析了不同荷载大小、荷载作用高度以及不同土质条件下筒壁土压力的分布规律, 结合圆弧段筒壁土压力的分布特点, 提出了较为简便的土压力计算方法。
筒型基础结构相比挡土墙的土压力计算更为复杂, 仍没有形成完善的理论计算方法, 其计算主要存在以下难点:
(1) 筒型基础与土体接触面一般为弧面, 这和挡土墙的土压力计算有所不同。
(2) 筒型基础在风浪荷载作用下并非产生平动位移, 而是发生转动。根据转动中心的不同, 两侧土体的受力状态也会有所差异。
(3) 实际工程中, 常常要求筒型基础的位移和倾角很小, 例如允许海上风电机正常工作的倾角一般较小, 此时筒型基础周围土体尚未达到极限平衡状态。
结合以上难点, 本文通过非极限平衡状态下的主被动土压力理论对风浪荷载作用下筒型基础的筒壁土压力进行研究, 首先参考挡土墙的土压力计算理论, 得到土压力与挡土墙位移之间的计算式, 然后分析筒型基础转动时的位移特点, 计算筒体任意点的水平位移, 最后求得筒体纵向和环向的土压力分布。
1 挡土墙位移与土压力计算如果将挡土墙视为刚性, 其位移模式主要分为5类[4]:平移、绕墙顶转动、绕墙底转动、绕墙顶部一点转动和绕墙底部一点转动。当位移或转角相对较小时, 墙后土体不能达到极限平衡状态, 此时的土压力计算, 需考虑挡土墙各点的位移[5]。根据相关文献[6], 土压力与挡土墙位移之间的大致关系如图 1所示。

|
图 1 土压力与挡土墙位移的关系 Figure 1 Relationship between earth pressure and displacement of retaining wall |
若挡土墙相对土体不发生侧向移动, 此时作用在挡土墙上的土压力为静止土压力p0; 当挡土墙背离土体方向移动并使墙后土体达到极限平衡状态时, 作用在墙体的土压力即主动土压力pa, 对应的位移量为sa; 当挡土墙向土体方向移动并使墙后土体达到极限平衡状态时, 作用在墙体的土压力即被动土压力pp, 对应的位移量为sp。3种土压力的关系如下:
| $ {p_{\rm{a}}} < {p_0} < {p_{\rm{p}}} $ | (1) |
实际工程中, 墙后土体可能没有达到极限平衡状态, 若位移量s介于sa与0之间, 称此时的土压力为准主动土压力p′a, 若位移量s介于0与sp之间, 称此时的土压力为准被动土压力p′p[7]。
为方便进一步计算, 一般对图 1曲线进行非线性拟合[8-9], 进而得到准主、被动土压力的表达式。此处采用文献[7]的拟合方法, 分别采用如下函数拟合准主动土压力和准被动土压力曲线:
| $ p^\prime{ _{\rm{a}}} = \frac{{{p_0}}}{{1 + A\left( \varphi \right)\sqrt[3]{{\frac{{s^\prime{ _{\rm{a}}}}}{{{s_{\rm{a}}}}}}}}} -\frac{{2c\frac{{s^\prime{ _{\rm{a}}}}}{{{s_{\rm{a}}}}}}}{{1 + B\left( \varphi \right)\frac{{s^\prime{ _{\rm{a}}}}}{{{s_{\rm{a}}}}}}} $ | (2) |
| $ p^\prime{ _{\rm{p}}} = {p_0}(1 + \frac{{\sqrt[3]{{\frac{{s^\prime{ _{\rm{p}}}}}{{{s_{\rm{p}}}}}}}}}{{D\left( \varphi \right) + \frac{{E\left( \varphi \right)s^\prime{ _{\rm{p}}}}}{{1 + \frac{{8c}}{{\gamma z}}{s_{\rm{p}}}}}}}) $ | (3) |
式中:静止土压力p0=k0γz, k0为静止土压力系数, γ为土的重度:A(φ), B(φ), D(φ), E(φ)为土体内摩擦角的函数。经多次拟合, 与ka(朗肯主动土压力系数), kp(朗肯被动土压力系数)和k0之间大致存在如下关系:
| $ \begin{array}{l} A\left( \varphi \right) = \frac{1}{{4.7}}{\rm{ln}}\left( {\frac{{{k_{\rm{p}}} + {k_{\rm{a}}}}}{{{k_{\rm{a}}}}}} \right)\\ B\left( \varphi \right) = \frac{{{k_{\rm{p}}}-{k_{\rm{a}}}}}{{{k_{\rm{p}}} + {k_{\rm{a}}} + {k_0}}}\\ D\left( \varphi \right) = \frac{{{k_{\rm{p}}} + 1.16{k_{\rm{a}}}}}{{0.96k_p^3}}\\ E\left( \varphi \right) = \frac{{{k_{\rm{p}}} + 1.16{k_{\rm{a}}}}}{{1.79k_p^3}} \end{array} $ | (4) |
特别地, 当s′a, s′p=0时, s′a=sa; 当s′a=sa时, p′a=pa; 当s′p=sp时, p′p=pp。
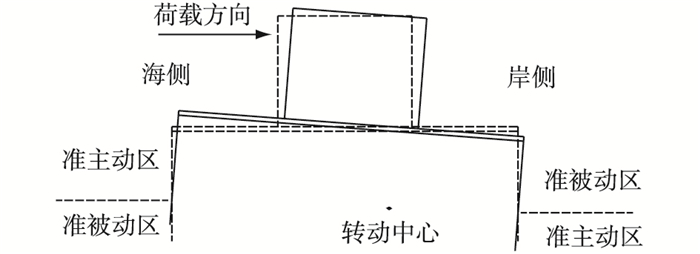
2 筒型基础土压力分布特点海上筒型基础相比挡土墙的位移模式更加复杂, 一般而言, 挡土墙5种位移模式下的转动中心都在墙体的外延长线上(平移可视为转动中心在无穷远处), 因此转动后, 墙上各点位移方向一致, 不会同时产生准主动土压力和准被动土压力, 只会产生其中的一种土压力。然而, 研究表明, 筒型基础的转动中心较为复杂, 根据地基土质和基础结构的不同, 转动中心可能在结构内部, 也可能在结构外部[10], 此外, 随着荷载水平变化, 转动中心也会变化。
一般而言, 在波浪荷载作用下, 临海侧侧壁以准主动土压力为主, 而临岸侧土压力以准被动土压力为主[11]。特别情况是当转动中心在结构内部时(见图 2)结构转动后同一侧面上的水平位移即有正值也有负值(设向岸侧位移为正), 因此临岸侧的结构侧面, 以位移零点分界, 上部为准被动区, 受准被动土压力作用, 下部为准主动区, 受准主动土压力作用。同理, 临海侧的结构侧面也可从上往下分为准主动区和准被动区。
|
图 2 筒型基础转动示意 Figure 2 Bucket foundation rotation diagram |
临海侧的结构侧面如果存在准被动区, 则筒体底部土压力会出现较快增大的现象, 而临岸侧的结构侧面如果存在准主动区, 筒体底部土压力会有所减小, 即纵向上的土压力会呈拱形分布[12-13]。
3 筒型基础土压力计算如果忽略侧壁各点竖向位移产生的影响, 计算筒型基础土压力的关键在于计算各点的水平位移。筒壁上的土压力计算主要包括两个部分, 一是纵向的土压力分布, 计算方法与挡土墙类似; 二是环向的土压力分布, 需要考虑结构的具体形状。为简化计算, 此处只对最为常见的圆柱形单桶结构进行计算, 该方法也能给其他结构类型的土压力计算提供参考。
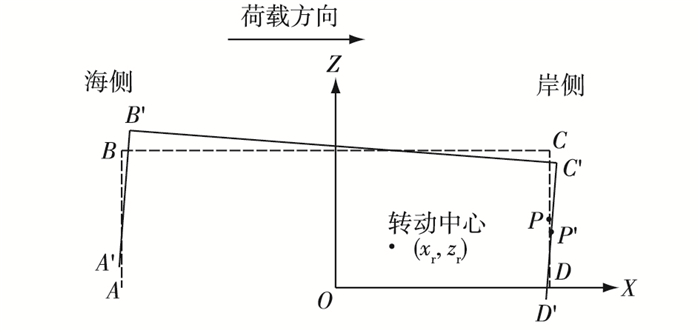
3.1 纵向土压力计算将筒型基础下部结构简化, 转动前后的筒体侧面图如图 3所示。
|
图 3 筒型基础转动计算 Figure 3 Calculation of bucket foundation rotation |
设转动中心坐标为(xr, zr), 则顺时针旋转角度为θ时, 筒体上任一点(x, z)旋转后的坐标为
| $ \left( {\begin{array}{*{20}{c}} {x^\prime }\\ {z^\prime } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{\rm{cos}}\theta }&{{\rm{sin}}\theta }\\ {-{\rm{sin}}\theta }&{{\rm{cos}}\theta } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {x-{x_r}}\\ {z-{z_r}} \end{array}} \right) + \left( {\begin{array}{*{20}{c}} {{x_r}}\\ {{z_r}} \end{array}} \right) $ | (5) |
以临岸侧侧壁CD上一点P(R, z)为例, 可得此点的水平位移
| $ s = x^\prime-x = ({\rm{cos}}\theta-1)(R-{x_r}) + {\rm{sin}}\theta (z - {z_r}) $ | (6) |
当水平位移s>0时, 利用式(3)可求得其准被动土压力, 当s≤0时, 可利用式(2)求得其准主动土压力。临海侧侧壁的土压力计算与之同理。
由式(2), (3)可知, 在土体参数给定的情况下, 土压力的大小只是水平位移s和深度z的函数。因此为使表达更为简洁, 可设由式(2), (3)组成的土压力计算函数为p(x, z), 从而得点(x, z)土压力计算式为
| $ p = p(({\rm{cos}}\theta-1)(R-{x_r}) + {\rm{sin}}\theta (z-{z_r}), z) $ | (7) |
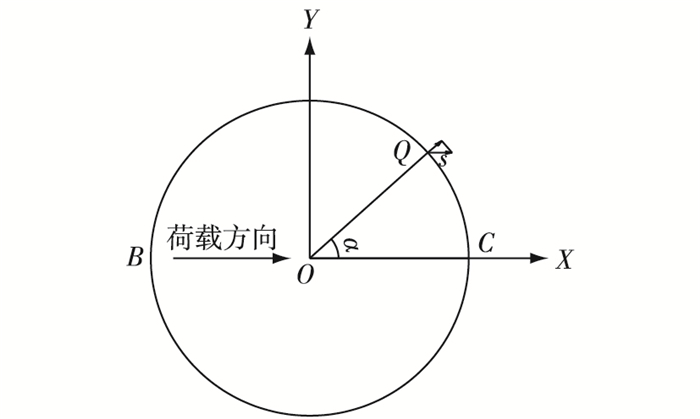
取筒体高度为z处的横截面, 如图 4所示。仍以临岸侧侧壁为例, 对筒壁上任一点Q, 设其与加载方向的夹角为α, 此时Q点三维坐标可表示为(Rcosα, Rsinα, z)。计算旋转后的水平位移为:
| $ s = {\rm{(cos}}\theta-1)(R{\rm{cos}}\alpha-{x_r}) + {\rm{sin}}\theta (z-{z_r}) $ | (8) |
|
图 4 环向土压力计算 Figure 4 Calculation of circumferential earth pressure |
由于Q点对应的切平面是斜平面, 故取其法向位移scosθ计算其法向土压力, 得
| $ p = p({\rm{cos}}\alpha \left[{({\rm{cos}}\theta-1)(R{\rm{cos}}\alpha-{x_r}) + {\rm{sin}}\theta (z-{z_r})} \right], z) $ | (9) |
临海侧侧壁的环向土压力计算与之同理。
4 计算结果分析 4.1 纵向土压力计算结果对比采用连云港徐圩港区直立式结构防波堤工程中的实测数据, 对本文计算结果进行对比。防波堤入土10.5 m, 长度为30 m, 在波浪荷载作用下的倾角为0.21°。在临海侧侧壁深度为1.5, 3.5, 5.5, 7.5和9.5 m处, 均匀布置了5个土压力传感器和相应的孔压传感器。地基土层以淤泥质土为主, 具体参数如下:重度6.8 kN/m3, 内摩擦角5.35 °, c′=9 kPa, k0=0.91(静止土压力系数采用公式k0=1-sinφ′计算。)
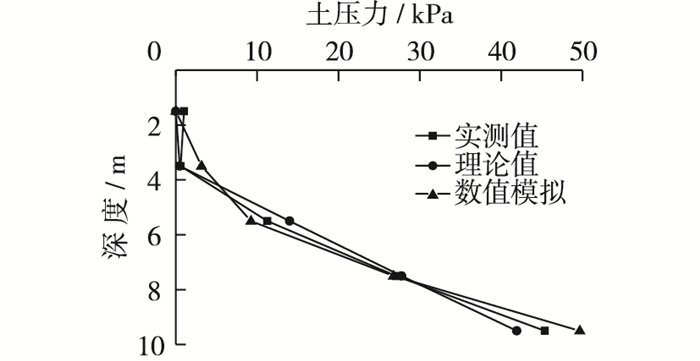
经过现场位移和倾角的观测数据, 得出筒体的转动中心大致在深度为-13.5 m, 距中轴线(偏向海侧)5 m的位置。取sa=0.004H [14], 即可求得各点的土压力理论值。基于本工程建立Abaqus有限元分析模型, 理论值、实测值和数值模拟结果三者对比见图 5。
|
图 5 筒壁纵向土压力对比 Figure 5 Longitudinal earth pressure variation on lateral wall |
由图 5可见:理论值与实测值比较接近, 理论计算结果基本能满足工程需求。而数值模拟的结果, 所得的零土压力的深度偏小, 在较小深度范围内存在一定误差。
4.2 环向土压力计算结果对比由于现场并未沿环向布置土压力计, 此处参考文献[3]中的有限元计算结果。分别对深度为8.5, 6.5和4.4 m处的环向土压力进行计算, 得出土压力与cosα之间的关系, 将其与数值模拟结果进行对比, 如图 6所示。

|
图 6 筒壁环向土压力对比 Figure 6 Circumferential earth pressure variation on lateral wall |
由图 6可见, 总体而言, 计算结果与有限元计算结果较一致, 仅在深8.5 m处环向土压力计算结果偏差稍大, 初步分析其原因是两种计算方法本身的差异所致。此外, 据该文献研究表明, 在倾角较小的情况下, 筒壁的环向土压力与cosα近似为线性关系, 本文的土压力计算方法, 基本体现了这一特点。
5 结语(1) 海上筒型基础在风浪荷载作用下, 并不总能达到极限平衡状态, 其筒壁土压力的计算可采用考虑位移的土压力计算理论。
(2) 荷载作用下, 筒型基础在临海侧侧壁以准主动土压力为主, 而临岸侧土压力以准被动土压力为主。特别是当转动中心在结构内部时, 侧面上会同时存在准主动区和准被动区。
(3) 本文采用的土压力计算方法, 与现场实测结果和有限元计算结果基本一致, 且能够反映出当结构倾角较小时, 环向土压力与cosα近似呈线性这一特点。
| [1] |
王元战, 肖忠, 李元音, 等. 筒型基础防波堤土压力性状的有限元分析[J]. 岩土工程学报, 2009, 31(4): 622-627. ( WANG Yuanzhan, XIAO Zhong, LI Yuanyin, et al. Finite element analysis for earth pressure on bucket foundation of breakwater[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 622-627. (in Chinese)) |
| [2] |
蒋敏敏, 蔡正银, 肖昭然. 箱筒型基础防波堤基础筒土压力数值模拟研究[J]. 水运工程, 2012(3): 20-23, 72. ( JIANG Minmin, CAI Zhengyin, XIAO Zhaoran. Numerical study on earth pressure on foundation bucket of bucket foundation breakwater[J]. Port & Waterway Engineering, 2012(3): 20-23, 72. (in Chinese)) |
| [3] |
蔡正银, 杨立功, 关云飞, 等. 新型桶式基础防波堤单桶桶壁土压力数值分析[J]. 水利水运工程学报, 2016(5): 39-46. ( CAI Zhengyin, YANG Ligong, GUAN Yunfei, et al. Numerical analysis of soil pressure on single bucket wall of new bucket foundation breakwater[J]. Hydro-Science and Engineering, 2016(5): 39-46. (in Chinese)) |
| [4] |
卢坤林, 朱大勇, 杨扬. 任意位移模式刚性挡土墙土压力研究[J]. 岩土力学, 2011, 32(增刊1): 370-375. ( LU Kunlin, ZHU Dayong, YANG Yang. Approximate calculation method of active earth pressure considering displacement[J]. Rock and Soil Mechanics, 2011, 32(Suppl1): 370-375. (in Chinese)) |
| [5] |
FANG Y S, CHEN T J, WU B F. Passive earth pressures with various wall movements[J]. Journal of Geotechnical Engineering, 1994, 120(8): 1307-1322. DOI:10.1061/(ASCE)0733-9410(1994)120:8(1307) |
| [6] |
梅国雄, 宰金珉. 考虑位移影响的土压力近似计算方法[J]. 岩土力学, 2001, 22(1): 83-85. ( MEI Guoxiong, ZAI Jinmin. Earth pressure calculating method considering displacement[J]. Rock and Soil Mechanics, 2001, 22(1): 83-85. (in Chinese)) |
| [7] |
卢国胜. 考虑位移的土压力计算方法[J]. 岩土力学, 2004, 25(4): 586-589. ( LU Guosheng. A calculation method of earth pressure considering displacement[J]. Rock and Soil Mechanics, 2004, 25(4): 586-589. (in Chinese)) |
| [8] |
姚国圣. 考虑位移的土压力计算方法在基坑工程中的应用[J]. 岩土工程学报, 2013, 35(增刊2): 693-696. ( YAO Guosheng. Application of earth pressure calculation method considering displacement in excavation engineering[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(Suppl2): 693-696. (in Chinese)) |
| [9] |
杨泰华, 贺怀建. 考虑位移效应的土压力计算理论[J]. 岩土力学, 2010, 31(11): 3635-3639, 3650. ( YANG Taihua, HE Huaijian. Earth pressure calculation theory considering displacement effects[J]. Rock and Soil Mechanics, 2010, 31(11): 3635-3639, 3650. DOI:10.3969/j.issn.1000-7598.2010.11.045 (in Chinese)) |
| [10] |
PARK J S, PARK D. Vertical bearing capacity of bucket foundation in sand overlying clay[J]. Ocean Engineering, 2017(134): 62-76. |
| [11] |
VAITKUNAITE E, NIELSEN B N, IBSEN L B. Bucket foundation response under various displacement rates[J]. International Journal of Offshore and Polar Engineering, 2016, 26(2): 116-124. DOI:10.17736/10535381 |
| [12] |
刘永刚, 丁红岩, 张浦阳. 淤泥质黏土中复合筒型基础水平承载力试验研究[J]. 岩土工程学报, 2016, 38(12): 2315-2321. ( LIU Yonggang, DING Hongyan, ZHANG Puyang. Model tests on bearing capacity of composite bucket foundation in clay[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(12): 2315-2321. (in Chinese)) |
| [13] |
施晓春, 龚晓南, 徐日庆. 水平荷载作用下桶形基础性状的数值分析[J]. 中国公路学报, 2002, 15(4): 49-52. ( SHI Xiaochun, GONG Xiaonan, XU Riqing. Numerical analysis of properties of bucket foundation under horizontal forces[J]. China Journal of Highway and Transport, 2002, 15(4): 49-52. (in Chinese)) |
| [14] |
卢坤林, 杨扬. 考虑位移影响的主动土压力近似计算方法[J]. 岩土力学, 2009, 30(2): 553-557. ( LU Kunlin, YANG yang. Approximate calculation method of active earth pressure considering displacement[J]. Rock and Soil Mechanics, 2009, 30(2): 553-557. (in Chinese)) |
 2018
2018 
