板桩结构是码头三大结构型式之一,以结构形式简单、造价低廉、施工周期短等优点,在国外众多港口码头建设中得到广泛应用。然而,由于我国长期缺乏用于建造板桩岸壁的优质型钢以及大倾角斜桩施工技术不足,导致板桩码头在规模和结构形式上受到极大限制,板桩码头仅用于中小型码头泊位,其主要结构型式为钢筋混凝土单锚板桩码头和斜拉桩式板桩码头。自2000年以来,钢筋混凝土地连墙板桩码头结构设计水平和施工技术在我国得到快速发展,先后成功研发了半遮帘式、全遮帘式和分离卸荷式板桩码头结构,在渤海湾数十个大型深水泊位建设中得到成功应用[1]。结合这些板桩码头新结构工程的设计与优化需要,开展了一系列土工离心模型试验[2-8],不仅对各种设计方案进行了充分论证,而且从不同角度揭示了板桩码头结构与地基相互作用机制,加深了其工作机理的认识,为地连墙板桩码头结构设计优化提供了依据。
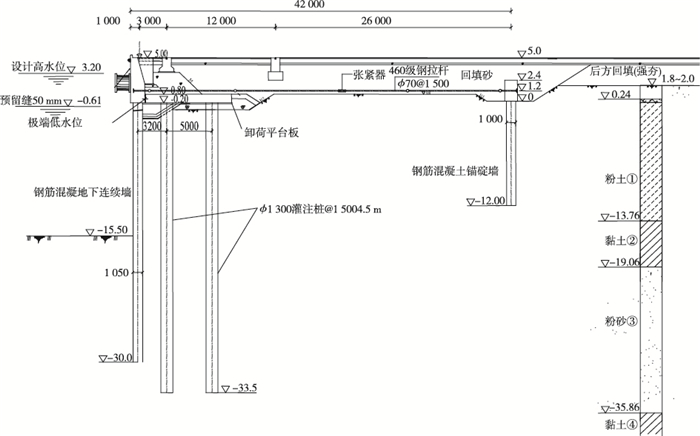
在上述板桩码头结构中,遮帘式板桩码头结构一般用于地基承载力较好的粉砂质地区,当地基中存在不良土层时,则选择适应能力更强的分离卸荷式板桩码头结构。盐城港滨海港区北区码头一期工程为10万t级通用泊位,码头前沿泥面标高-15.5 m,由于其码头地基中存在一层厚度约5.3 m黏土层,其标贯击数6.5击,允许承载力100 kPa,压缩系数0.78 MPa-1,属于高压缩性土,故码头结构采用了图 1所示的分离卸荷式地连墙板桩结构。其中钢筋混凝土地连墙、锚碇墙和卸荷承台板厚度分别为1.05, 1.00和1.00 m,两排钢筋混凝土灌注桩直径1.30 m,间距4.5 m,钢锚杆直径70 mm,间距1.5 m。鉴于高压缩性黏土层中线高程约-16.4 m,其埋深处于码头前沿泥面附近,对码头结构受力稳定影响较大,鉴于本工程是盐城港滨海港区第一个大型地连墙码头工程,故开展了4组土工离心模型试验对该码头设计方案合理性和码头结构稳定性进行验证,本文给出了其中最典型的1组模型试验及其分析结果。
|
图 1 原型码头结构断面(单位:标高,m;其他,mm) Figure 1 Prototype wharf structure section (unit: elevations in m; others in mm) |
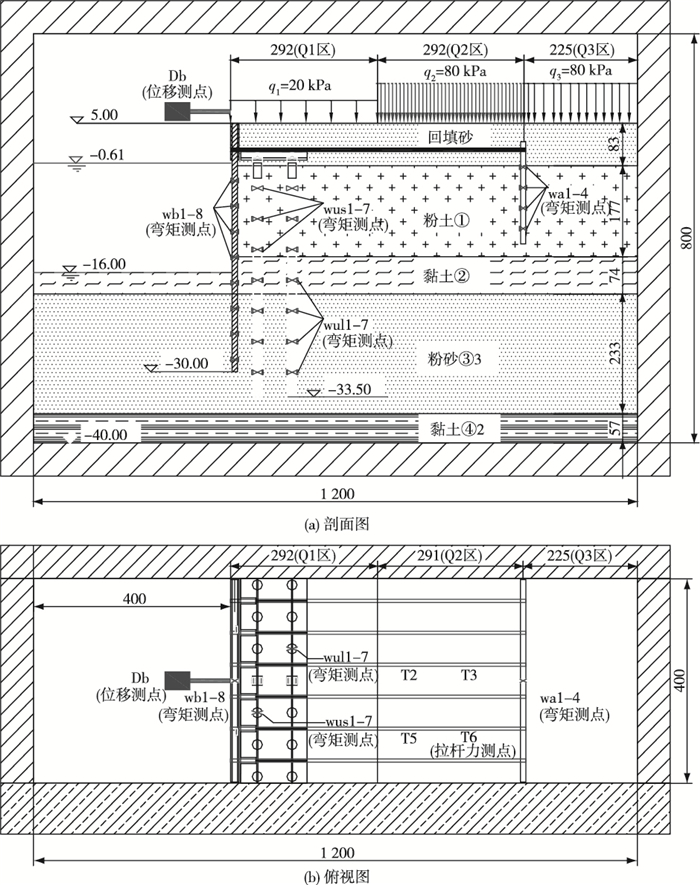
试验在南京水利科学研究院400 g-t土工离心机完成,该离心机旋转半径为5.5 m,最大离心加速度为200g,相应最大负荷为2 000 kg,容量400 g-t。图 1为所设计的10万t级卸荷式板桩码头结构原型断面。因码头沿岸线布置,模型布置可按平面应变问题考虑,故试验采用了大型平面应变型模型箱,其净空尺寸为1 200 mm(长)×400 mm(宽)×800 mm(高)。模型布置时,根据图 1所示的原型码头结构尺寸和受力后在地基中的影响范围,为避免模型箱端壁对模型地连墙结构物的边界约束影响[9],选定的原型与模型几何相似比为72,即n=72,其他物理量根据离心模型试验相似准则确定[5],模型布置见图 2。为了考虑原型港池开挖中的超挖影响,模型港池泥面线确定为-16.0 m(图 2)。
|
图 2 模型布置(单位:标高, m;其他,mm) Figure 2 Model layout (unit: elevations in m; others in mm) |
模型地基采用原型土料,在室内重塑制备而成。如图 1所示,地基土层自上往下分别为回填砂层、粉土层①、黏土层②、粉砂层③3、黏土层④2。其中回填砂层、粉土层①和粉砂层③3属于无黏性土层,采用压实法制备,按其重度进行控制(表 1)。黏土层②和④2属于黏性土层,采用预压排水固结法制备[10],按表 1中所要求的原位不排水强度值进行控制,即先将黏土土料制备成泥浆,然后注入模型箱内,移置于大型固结仪,待自重固结一定程度后,再在其上逐级施加预压荷载,使土层逐渐排水固结,期间定时监测土体强度的增长,直至其不排水强度达到所要求的目标值。
| 表 1 模型地基土层特性指标 Table 1 Properties of model soil ground |
从理论上说,土工离心模型中所有材料应选用与原型相同的材料进行制作,以确保两者性质完全一致。原型卸荷式板桩结构码头中的地连墙、锚碇墙和卸荷承台及直立灌注桩均为钢筋混凝土材料,按长度比例尺n=72缩制的这些模型结构件,其断面尺寸很小。若仍采用钢筋混凝土制作,这些结构件尺寸难以精确控制,更重要的是,在表面粗糙、尺寸很小的混凝土构件上难以粘贴应变片进行内力测量。考虑到钢筋混凝土和铝合金可近似视作弹性材料,且两者材料密度相近,因此,通常都是采用铝合金材料替代混凝土材料制作模型码头的结构件。
在板桩码头结构中,前板桩墙、锚碇墙和卸荷板都属于抗弯构件,因此,模型构件均按等抗弯刚度相似原理进行设计计算[2-6]。这样,用铝合金制作的模型地连墙、锚碇墙和卸荷承台板的尺寸,分别为414 mm(高)×10.7 mm(厚),167 mm(高)×10.2 mm(厚)和132 mm(长)×10.2 mm(厚),它们的宽度与模型箱宽度一致,都为400 mm。
卸荷平台下的直立圆截面灌注桩,既承受竖向荷载而受压,又抵抗侧向土压力作用承受侧向荷载而受弯。为了保持模型桩侧壁和土体之间的摩擦特性与原型一致,其外径需按几何比尺缩制,在此约束条件下再选择合适壁厚的铝合金管来模拟原型实心钢筋混凝土灌注桩。考虑到原型灌注桩侧向承受地基土体侧向位移而有较大的弯矩反应,因此,管壁厚度则根据桩体抗弯刚度相似原理进行调整。由于铝合金材料的弹性模量高于钢筋混凝土材料的弹性模量,因此,原型中的实心桩在模型中将由空心的铝合金管桩来模拟。设原型灌注桩的截面直径为ap,内径为bp,因为是实心桩,bp=0。模型桩截面直径为am,因ap与am之间必须保持几何相似,故am=ap/n。这时原型与模型桩截面惯性矩分别为:Ip=πap4/64,Im=π(am4-bm4)/64,这两者必须满足抗弯刚度相似关系要求,即满足EmIm=EpIp/n4,由此可以推导出模型桩截面内径为:
| ${{b}_{\text{m}}}={{a}_{\text{m}}}\sqrt[4]{(1-{{E}_{\text{p}}}/{{E}_{\text{m}}})~} $ | (1) |
对于直径ap=1 300 mm原型钢筋混凝土灌注桩,其弹性模量Ep=28 GPa,而模型桩采用铝合金制作,其弹性模量Em=70 GPa。在比尺n=72的模型中,外径am=1 300/72 =18 mm,按式(1)计算,bm≈16 mm。这样,就采用外径18 mm、壁厚1 mm的铝合金管制作模型桩,模型桩在卸荷板以下部分的长度为463 mm。
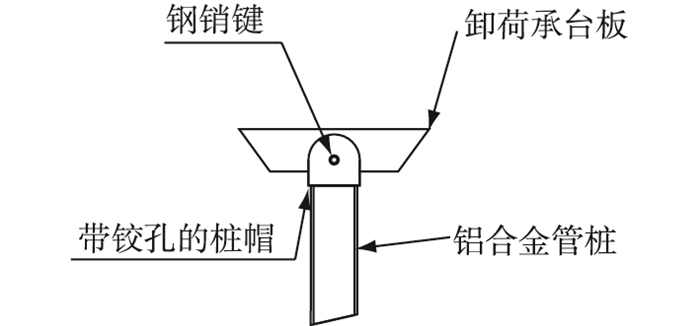
为了模拟原型卸荷平台与直立灌注桩之间的铰接,模型试验设计了文献[8]介绍的一种销键铰接,如图 3所示。
|
图 3 模型卸荷板与灌注桩的铰接 Figure 3 Sketch of connection between pile and relief plate |
板桩码头结构中的锚杆属于受拉构件,模型按等抗拉刚度相似原理进行设计[2-6]。已知原型460级钢锚杆直径为70 mm,模型锚杆采用同样的钢材料制作。为了配合模型直立灌注桩的布置,用1根模型锚杆代替3根原型锚杆,同时考虑锚杆拉力测试需要,根据以往测试经验,将圆截面锚杆变换为等面积的矩形截面锚杆。最终设计采用的模型钢锚杆截面尺寸为:7.4 mm(宽)×0.4 mm(厚),长度约586 mm。
1.3 模型测量NHRI 400 g-t大型土工离心机配备有专门的数据采集系统,可同时满足90个通道传感器的模型测量需要。模型试验主要测量的物理量包括地连墙、锚碇墙和两排直立灌注桩的弯矩、锚杆力和地连墙侧向变位,这些物理量的测点布置见图 2。其中,地连墙锚着点处的侧向位移,采用德国Wenglor公司的激光传感器测量,规格为YP11MGVL80,量程为50 mm,相应的精度为20 mm;弯矩和锚杆力通过粘贴微型应变计搭建全桥电路进行测量[3, 6]。如图 2所示,在地连墙上部布置了1个侧向位移测点Db,在地连墙墙身上布置了8个弯矩测点wb1~wb8,在锚碇墙墙身上布置了4个弯矩测点wa1~wa4,在第3根海侧灌注桩和第5根陆侧灌注桩上各布置7个弯矩测点wus1~wus7和wul1~wul7,在第2根和第4根锚杆上各布置了4个轴力测点T2~T3和T5~T6。
1.4 荷载模拟板桩结构码头受到的侧向荷载来自地连墙陆侧地基土体侧向位移所形成的土压力,其大小与直立凌空面高度以及墙前水位相关。工程码头面和港池泥面标高分别为5.0和-16.0 m,故凌空面高度为21.0 m,当港池水位处于极端低水位-0.61 m时,地连墙海陆侧两侧水压力和土压力共同形成的压力差达到最大,本次模型试验模拟这一最为恶劣的受力工况。对于港池水位,采用常规的溢流法进行控制,保持极端低水位。至于地连墙港池一侧的侧向卸载,受制于当前的设备技术水平,港池开挖尚不能在模型运转至设计加速度条件下模拟,仍采用在地面1g条件下开挖,其后通过升高离心加速度进行模拟。马险峰等对这种地面预开挖而后再升速的模拟方法进行过相关研究,其误差处于岩土工程可接受程度内,仍是当前最务实的做法[11]。
另外,码头面上的堆载是最主要的竖向荷载,原型码头面堆场分为2个区域,第1个区域位于前沿线后21 m范围内,堆货均载为20 kPa;第2个区域位于21m范围以外,均载为80 kPa。相应地,模型码头面第1个区域Q1为前沿线后长292 mm,宽400 mm范围,面积为0.116 8 m2,荷载集度为20 kPa,这一区域上的荷载采用质量法施加模拟,即在此面积上铺设铅砂,使其在设计加速度条件下产生20 kPa均布荷载,如图 2所示。码头面第2个区域位于第1个区域后,范围长516 mm,宽400 mm,荷载集度为80 kPa。为了考虑这一区域最不利荷载分布,即锚碇墙之前无堆载,其他区域满堆载,故以锚碇墙为界,将80 kPa面载区域划分为长291 mm的Q2区和长225 mm的Q3区,如图 2所示。分别在Q2区和Q3区放置尺寸大小合适的两只铁皮水盒,在模型运转至设计加速度后,按最不利的加载顺序模拟码头面竖向荷载的施加,即先给Q3区水盒注水,再给Q2区水盒注水,通过水盒产生的水荷载,实现这两个区域的码头面荷载模拟。
1.5 试验过程模型试验拟模拟自港池开挖形成的竣工期和投入营运的运行期。参照近年兴建的多个10万t级板桩码头泊位港池浚深形成所需时长,确定本次模型试验所模拟的原型码头前沿浚深挖泥时长为6个月,在n=72土工离心模型试验中,约需运行50 min。另外模拟原型码头投入营运7个月左右,约216 d,约需运行60 min。
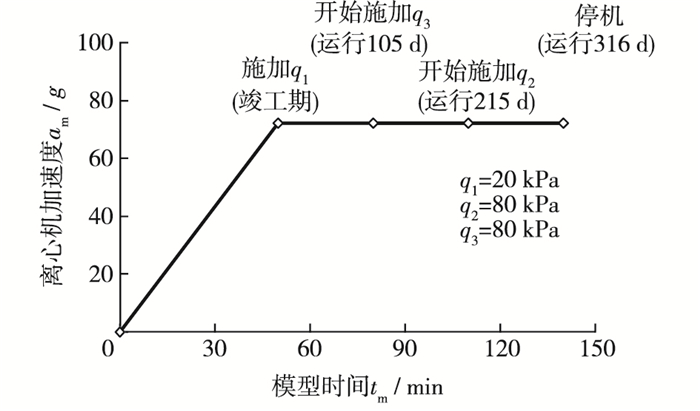
如前所述,为了模拟原型最不利的码头面荷载分布,离心加速度上升和荷载施加的时间过程见图 4。在码头面Q1区采用质量加载法,当模型加速度达到设计加速度72g时,码头面Q1区内的堆载q1也已同时施加。继续恒加速度运行30 min后,开始向Q3区的水盒内注水加载,相当于在原型港池形成108 d后开始在码头面上堆载q3,此次注水加载及之后运行共计30 min,该时长相当于原型时长108 d。最后,再向Q2区域的水盒注水,注水加载q2及之后运行共计30 min,又模拟原型时长108 d。
|
图 4 模型试验过程 Figure 4 Model test process diagram |
需要说明的是,下面所述弯矩、锚杆力和位移,已经按照文献[6]中给出的各物理量模型相似率,分别换算成原型尺度的数值,模型试验得到的码头性状特征值见表 2。
| 表 2 码头性状特征值 Table 2 Characteristic values of wharf behavior |
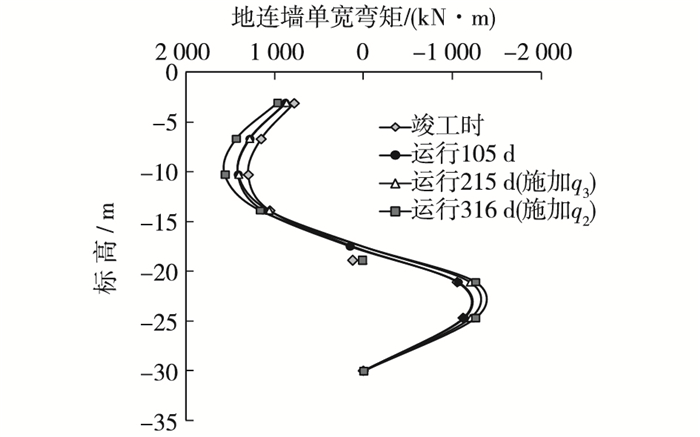
图 5是地连墙墙身单宽弯矩分布情况,图中给出了浚深形成港池竣工时(有q1),竣工后运行105 d(q1),215 d(q1和q3)和316 d(q1,q2和q3)的4条弯矩分布曲线。从图 5中4条曲线上下各部分的重合程度可以看到整个试验过程中地连墙墙身弯矩的发展变化,与竣工时相比,竣工后运行105 d时,地连墙墙身上部正弯矩稍有增长,但墙身下部基本未变。
|
图 5 地连墙单宽弯矩分布 Figure 5 Unit width bending moment of diaphragm wall |
在锚碇墙后场区域Q3内施加q3后继续运行至215 d,墙身上部弯矩未见明显变化,但墙身下部负弯矩增长,最大负弯矩点处的弯矩增量达-128 kN·m/m,表明后场区域Q3内的面载q3只对地连墙墙身下部有影响。
在码头面中间区域Q2内施加q2后继续运行至316 d,墙身上部正弯矩值和下部负弯矩值均出现明显增长,但上部正弯矩反应更显著,最大正弯矩点处的弯矩增量达154 kN·m/m,并且上部正弯矩增量明显多于墙身下部负弯矩增量,表明中间区域Q2内的面载q2对地连墙墙身上下部均有影响。
从图 5可见,地连墙在标高-10.0 m和-22.5 m的弯矩内力值是其弯矩分布曲线的极值点,施加q2前后,最大单宽弯矩正负值分别为1 405, -1 199 kN·m/m和1 558, -1 226 kN·m/m(表 2),均在钢筋混凝土地连墙弯矩设计值以内。面载q3和q2共同作用后,地连墙墙身上部最大正弯矩点处的增量为148 kN·m/m,占最大正弯矩值的9%;墙身下部最大负弯矩点处的增量为-191 kN·m/m,占最大负弯矩值的15%。
另外,图 5中4条弯矩曲线反弯点几乎重合,位于墙身标高约-17.5 m,即港池泥面线(-16.0 m)以下1.5 m。对照文献[6]中地连墙板桩码头结构模型试验结果,地连墙弯矩曲线反弯点位于墙身标高-17.2 m, 港池泥面线(-16.5 m)以下0.7 m处。试验结果中地连墙弯矩曲线反弯点较低的原因,在于地基土层中靠近泥面线的高压缩性黏土层,它的存在致使弯矩曲线特征点向下偏移。
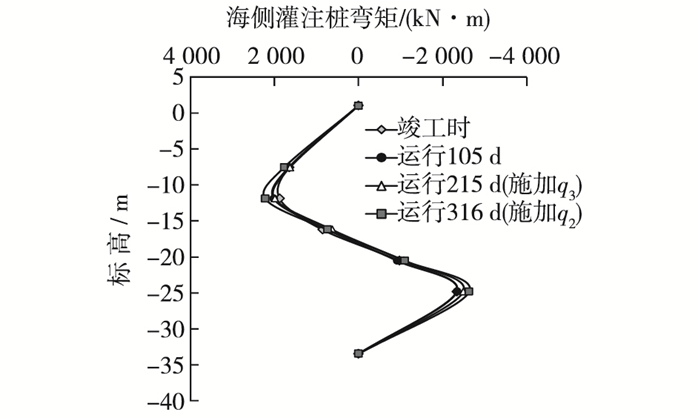
2.2 灌注桩桩身弯矩图 6和图 7是海陆两排灌注桩桩身弯矩分布,分别是竣工时(q1),竣工后运行105 d(q1), 215 d(q1和q3), 和316 d(q1,q2和q3)的4条桩身弯矩分布曲线。从上下各部分的重合程度可以看到不同阶段海侧桩桩身弯矩的发展变化,与竣工时相比,竣工后运行105 d时,海侧桩桩身上部正弯矩略有增长,但其下部基本未变。
|
图 6 海侧桩弯矩分布 Figure 6 Bending moment of seaside pile |

|
图 7 陆侧桩弯矩分布 Figure 7 Bending moment of landside pile |
从图 6可以看出,在锚碇墙后场区域Q3内施加q3后继续运行至215 d,海侧桩桩身上部弯矩并未明显变化,但桩身下部负弯矩出现了增长,在桩身下部的最大负弯矩点处,弯矩增量达-150 kN·m,表明区域Q3内的面载q3对海侧桩桩身下部有较强影响。在码头面中间区域Q2内施加q2后继续运行至316 d,海侧桩桩身上部正弯矩和下部负弯矩均出现了增长,但上部影响更明显,其上部的最大正弯矩点处,弯矩增量达231 kN·m,下部最大负弯矩点的增量为-132 kN·m,表明区域Q2内的面载q2对海侧桩桩身上下部均有影响,且上部弯矩反应更大。
施加q2前后,海侧灌注桩最大正负弯矩分别为1 983, -2 487 kN·m和2 214, -2 618 kN·m,相应位置标高分别约为-11.0和-24.5 m。面载q3和q2共同作用后,桩身上部最大正弯矩点处增量为204 kN·m,占最大正弯矩值的9%;桩身下部最大负弯矩点处的增量为-282 kN·m,占最大负弯矩值的11%。
从图 7可以看出,对于陆侧灌注桩,与竣工时相比,竣工后运行105 d时,桩身上部正弯矩略有增长,但其下部基本未变。在锚碇墙后场区域Q3内施加q3后继续运行至215 d,陆侧桩桩身下部弯矩出现明显增长,尤其是在桩身下部的最大负弯矩点处,弯矩增量达-456 kN·m,表明区域Q3内的面载q3对陆侧桩桩身下部影响显著。但在码头面中间区域Q2内施加q2后继续运行至316 d,陆侧桩桩身上部正弯矩出现了较明显增长,在桩身上部最大正弯矩点处,弯矩增量达223 kN·m,而下部桩身弯矩变化不多,表明区域Q2内的面载q2对陆侧桩桩身上部影响较为明显。总的来说,Q3区域内的面载q3对陆侧桩下部影响显著,Q2区域内的面载q2对桩身上部影响明显。
施加q2前后,最大正负弯矩分别为2 185, -2 363 kN·m和2 408, -2 401 kN·m,相应的位置标高分别约为-11.0和-24.5 m。面载q3和q2共同作用后,桩身上部最大正弯矩点处的增量为256 kN·m,占最大正弯矩值的11%;桩身下部最大负弯矩点处的增量为-493 kN·m,占最大负弯矩值的21%。
另外,图 6和7所示海陆两排灌注桩弯矩分布曲线中的反弯点位置标高分别约在-17.5和-18.0 m处。与文献[6]中两排灌注桩弯矩曲线反弯点位置(-12.5和7.0 m)相比,试验结果中灌注桩弯矩曲线反弯点位置明显较低,其原因仍是地基土层中靠近泥面线的高压缩性黏土层所致,它的存在使得两排灌注桩弯矩曲线特征点显著向下偏移,表明灌注桩将地基上部土体侧向位移作用更进一步向深部地基土体传递。
综上所述,两排灌注桩对码头面的80 kPa面载作用的弯矩反应非常明显。海陆两排桩最大正弯矩分别增大了9%和11%,其最大负弯矩数值则分别增大了11%和21%。Q3区域内的面载q3使两排桩下部负弯矩数值发生了增长,而Q2区域内的面载q2主要使两排桩的上部正弯矩发生了增长。
设置卸荷平台侧向群桩基础结构的目的,就是将原本作用于地连墙上的一部分土压力荷载转移传递至更深更广的土层中,确保地连墙和整个码头结构稳定,并控制地连墙水平位移量在允许范围内。文献[6]研究结果表明,设置卸荷平台群桩基础结构后,地连墙陆侧受到的土压力减小了,从而墙身弯矩反应和侧向位移相应减小。因此,卸荷平台群桩基础结构中的直立灌注桩桩身弯矩就是承担侧向土压力荷载后的反应标志。
下面以表 2中所列的两排灌注桩弯矩特征值为例,将其折合成单宽弯矩值,并将两者累加后与相应的地连墙特征值进行比较。在码头面3个区域的面载全部施加后,海侧桩和陆侧桩最大正弯矩分别达492和535 kN·m/m,合计达1 027 kN·m/m,是地连墙最大正弯矩值的66%,而海侧桩和陆侧桩最大负弯矩分别达-582和-534 kN·m/m,合计达-1 116 kN·m/m,是地连墙最大负弯矩值的88%。可见,卸荷平台下的两排灌注桩发挥了巨大的侧向承载作用,显著减轻了地连墙承担的侧向土压力荷载。
直径1.3 m钢筋混凝土灌注桩弯矩设计值约为2 900~3 050 kN·m,因此,两排灌注桩桩身弯矩反应未超出弯矩设计值,处于安全允许范围内。
2.3 锚碇墙墙身弯矩图 8是锚碇墙墙身弯矩分布,分别是竣工时(q1),竣工后运行105 d(q1), 215 d(q1和q3)和316 d(q1, q2和q3)的4条桩身弯矩分布曲线。所测得的锚碇墙墙身弯矩值都为负值,表现为墙身陆侧面受拉。图中前3条弯矩分布曲线比较接近,表明锚碇墙从竣工时直至在Q2区施加面载q2之前,锚碇墙墙身弯矩基本未出现明显变化,最大单宽负弯矩约-1 023 kN·m/m(表 2),在钢筋混凝土锚碇墙弯矩设计值以内。但在Q2区施加面载q2后,墙身弯矩数值出现明显变化,其最大负弯矩值点处的弯矩增量达-188 kN·m/m,最大单宽负弯矩约-1 210 kN·m/m(表 2),面载q2作用引起的弯矩增量占15%。

|
图 8 锚碇墙单宽弯矩分布 Figure 8 Unit width bending moment of anchor wall |
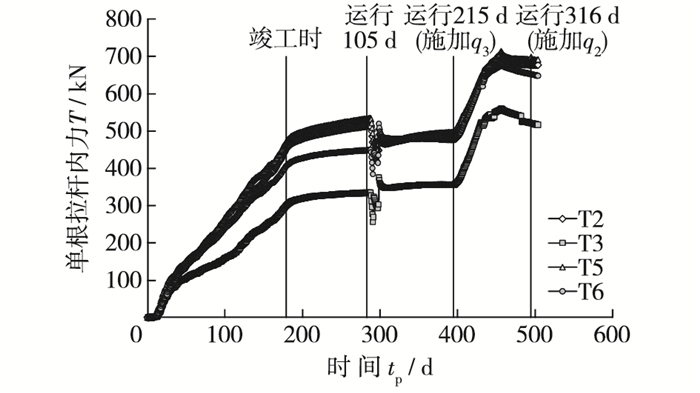
图 9是锚杆拉力随时间发展过程,在港池形成过程中,锚杆拉力增长最大,待竣工后,增长趋势明显放缓,逐渐趋于稳定。如图 9所示,拉力测点T2和T3位于同一根锚杆上,T2位于锚杆中点,T3偏向锚碇墙锚着点一侧。显然,T2处的拉力值明显大于T3处的拉力值,在施加Q3区域的面载q3和Q2区域的q2之前,T3/T2>85%。对于另一根测量锚杆上的测点T5和T6,锚杆拉力表现出相同的分布特征,在施加面载q3和q2之前,T6/T5>65%。这一特征表明同一根锚杆,其拉力从地连墙锚着点沿锚杆向锚碇墙锚着点逐渐变小。
|
图 9 锚杆力的发展曲线 Figure 9 Development curves of tension force of tie-rods with time |
然而,如图 9所示,在Q3区域施加面载q3后,4个测点处锚杆力出现了先降后升的突变过程,之后趋于平缓。从施加面载q3之后直到施加面载q2之前这段时间,位于锚杆中点处的2个测点T2和T5,其所在处锚杆力均出现了下降,增量分别约-19和-41 kN,而偏向锚碇墙锚着点的2个测点T3和T6,其所在处锚杆力均出现了上升,增量分别约21和28 kN。
在Q2区域施加面载q2后,4个测点处锚杆力均有增大过程,之后趋于平缓。位于锚杆中点处的2个测点T2和T5,其所在处锚杆力增幅较大,增量分别约为183和202 kN,而偏向锚碇墙锚着点的2个测点T3和T6,其所在处锚杆力增幅稍小,增量分别约为166和176 kN。
Q3区域施加面载q3后,位于锚杆中点2个测点处的锚杆拉力实测值平均值约为480 kN,而Q2区域施加面载q2后,位于锚杆中点2个测点处的锚杆拉力实测值平均值则约为610 kN(表 2)。对于直径70 mm的550级高强锚杆,锚杆力设计值可达1 900 kN,因此,锚杆受力处于安全允许范围内。
2.5 码头结构整体稳定性由于受空间限制,试验只对模型地连墙锚着点的侧向位移进行了测量。地连墙锚着点位移量主要是港池开挖施工期中产生积累的,竣工后只有少量位移,基本处于稳定,侧向位移量约45 mm。但在锚碇墙后方Q3区域施加面载q3后,地连墙锚着点侧向位移出现明显的增幅,侧向位移量达60 mm,增量约有10 mm,之后趋于平缓,而在锚碇墙前方Q2区域再施加面载q2后,地连墙锚着点侧向位移虽有增加,但增幅较小,最终位移量约61 mm(表 2)。
假设地连墙为刚体发生前倾,计算出的地连墙倾斜率为0.20%,该数值处于直立式板桩岸壁码头允许变形范围内[12]。模型试验完成后,通过检查发现,码头面无裂缝,结构整体完好,表明该工况条件下,码头结构整体稳定。
3 结语通过开展土工离心模型试验,成功模拟了盐城港滨海港所包含的高压缩性黏土层地基条件和板桩结构所承受的极端低水位和码头面最不利加载条件,观测了码头各构件的内力反应和地连墙侧向位移,结果表明,地连墙、锚碇墙和灌注桩弯矩以及锚杆拉力均趋于稳定,且处于各自安全允许范围内,只是地连墙和灌注桩弯矩反弯点位置比一般情况明显下移;地连墙锚着点位移和地连墙倾斜度均处于合理区间,码头结构整体稳定,充分验证了本板桩结构设计方案合理可靠,有效展示了分离卸荷式地连墙板桩码头结构对不利地基条件的适应能力。
(1) 卸荷式板桩码头结构与地基土体之间的相互作用是一个动态过程,港池开挖和面载施加会即刻引起构件较大的内力反应,但尚需一段时间的调整才能趋于平稳。试验发现,码头构件内力反应一般在竣工后100 d或面载施加后100 d基本达到稳定。
(2) 在离心模型运转过程中采用注水加载法模拟了真实的面载施加过程,码头面80 kPa面载作用显著,而且以锚碇墙为界,前后区域内面载效果不尽相同,后场Q3区域的面载对地连墙和灌注桩下部以及锚杆作用明显:最大正负弯矩绝对值增大,锚杆力减小,地连墙锚着点侧向位移增加;而中间Q2区域的面载对地连墙和灌注桩上部作用明显,最大正负弯矩绝对值增大,锚杆力增大。后场区域和中间区域的面载共同作用后,墙体和桩身的最大正负弯矩、锚杆力和地连墙锚着点侧向位移等特征值均增大,增幅一般在10%~20%。
(3) 两排灌注桩最大正弯矩合计值是地连墙最大正弯矩值的66%,最大负弯矩值是地连墙最大负弯矩值的88%,因此,卸荷承台群桩基础所发挥了显著的侧向承载作用。
需要说明的是,有多种因素会影响到离心模型试验测试结果,但鉴于离心模型试验中充分模拟了原型码头地基最不利条件和运行时最不利加载顺序,因此,试验结果能够预测并再现原型码头结构最不利工况中的工作性状。
| [1] |
刘永绣. 板桩式岸壁结构的设计理论与方法[M]. 北京: 人民交通出版社股份有限公司, 2014: 1-20. ( LIU Yongxiu. Design theories and methods for sheet-pile bulkhead[M]. Beijing: China Communications Press Co. Ltd, 2014: 1-20. (in Chinese))
|
| [2] |
李景林, 王剑平, 蔡正银, 等. 遮帘桩方案改造板桩码头离心模型试验研究[J]. 岩土工程学报, 2006, 28(8): 978-982. ( LI Jinglin, WANG Jianping, CAI Zhengyin, et al. Centrifuge model tests on sheet-piled wharf renovated by barrier pile project[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(8): 978-982. (in Chinese)) |
| [3] |
刘永绣, 吴荔丹, 徐光明, 等. 遮帘式板桩码头工作机制[J]. 水利水运工程学报, 2006(2): 8-12. ( LIU Yongxiu, WU Lidan, XU Guangming, et al. Working mechanism of sheet pile wharf with barrier piles[J]. Hydro-Science and Engineering, 2006(2): 8-12. (in Chinese)) |
| [4] |
XU G M, CAI Z Y, ZENG Y J, et al. Centrifuge modeling for a new type sheet pile bulkhead with barrier piles[C]//Proc Physical Modelling in Geotechnics—6th ICPMG'06. Talor & Francis Group, London, 2006: 1125-1129.
|
| [5] |
李景林, 蔡正银, 徐光明, 等. 遮帘式板桩码头结构离心模型试验研究[J]. 岩石力学与工程学报, 2007, 26(6): 1182-1187. ( LI Jinglin, CAI Zhengyin, XU Guangming, et al. Centrifuge modeling test on covered sheet-piled structure of wharf[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(6): 1182-1187. (in Chinese)) |
| [6] |
徐光明, 蔡正银, 曾友金, 等. 一种新型板桩码头结构的离心模拟[J]. 岩土力学, 2010, 31(增刊1): 48-52. ( XU Guangming, CAI Zhengyin, ZENG Youjin, et al. Centrifuge modeling for an innovative sheet-pile bulkhead of diaphragm[J]. Rock and Soil Mechanics, 2010, 31(Suppl1): 48-52. (in Chinese)) |
| [7] |
徐光明, 李士林, 刘永绣, 等. 板桩码头结构中桩体作用宽度试验研究[J]. 长江科学院院报, 2012, 29(1): 85-90. ( XU Guangming, LI Shilin, LIU Yongxiu, et al. Experimental investigation of equivalent breadth of pile in sheet-pile bulkhead[J]. Journal of Yangtze River Scientific Research Institute, 2012, 29(1): 85-90. (in Chinese)) |
| [8] |
徐光明, 李士林. 板桩码头中群桩基础联接型式的试验研究[J]. 岩石力学与工程学报, 2016, 35(增刊1): 3365-3371. ( XU Guangming, LI Shilin. Experimental study of head fixity conditions of pile group in sheet-pile bulkhead[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(Suppl1): 3365-3371. (in Chinese)) |
| [9] |
徐光明, 章为民. 离心模型中的粒径效应和边界效应研究[J]. 岩土工程学报, 1996, 18(3): 80-86. ( XU Guangming, ZHANG Weimin. A study of size effect and boundary effect in centrifugal tests[J]. Chinese Journal of Geotechnical Engineering, 1996, 18(3): 80-86. (in Chinese)) |
| [10] |
蒋敏敏, 徐光明, 顾行文. 离心模型试验饱和粘性土制备和固结分析[C]//第25届全国土工测试学术研讨会论文集. 杭州: 浙江大学电子音像出版社, 2008: 357-378. (JIANG Minmin, XU Guangming, GU Xingwen. Analysis of preparation and consolidation of saturated clay for centrifugal model test[C]//Proceedings of 25th National Symposium on New Geotechnical Testing. Hangzhou: Zhejiang University Electronic Audio and Video Press, 2008: 357-378. (in Chinese))
|
| [11] |
MA X F, HOU Y J, CAI Z Y, et al. Centrifuge modelling of geotechnical processes in soft ground using pragmatic approaches[C]//Proceedings of the 8th International Conference on Physical Modelling in Geotechnics. 2014: 139-151.
|
| [12] |
TSINKER G P. Handbook of port and harbor engineering: geotechnical and structural aspects[M]. ITP International Thomson Publishing: Chapman & Hall Press, 1997: 4775.
|
 2018
2018 