2. 西北农林科技大学 水利与建筑工程学院,陕西 杨凌 712100
黄土高原坐落于中国西北部,黄土沉积区面积为世界之最,跨晋陕甘青宁豫六省区,面积约40万km2。由于植被覆盖减少,土质蓬松,地形支离破碎,且降水多以短历时暴雨形式出现,使其成为世界上土壤侵蚀与水土流失程度最为严重的地域。因此,以典型小流域为研究对象,准确估算各类下垫面条件下的地表径流量,对进行黄土高原水土流失的预报和开展水土保持工程措施有着重要的生态意义和经济意义[1]。
SCS-CN(soil conservation service curve number)模型于19世纪30年代由美国农业部水土保持局根据当地环境开发,目前主要集中于地表径流预测、模型参数改进及与其他模型结合的研究。
(1) 地表径流预测。Karl Auerswald利用回归法计算CN值进行径流预测[2]。Bhuyan根据前5日降雨量预测前期土壤湿度,提高CN值精度,并在各种流域中进行径流预报[3]。张钰娴等根据50场实测降雨资料,研究初损率在合理范围内变化时不同坡度下的径流曲线数值[4]。李常斌等考虑了土地利用情况下的径流场资料,对标准SCS-CN模型进行推导反推得到CN值[5]。罗利芳等根据陕西安塞25个小区域实测降雨径流资料,计算黄土高原不同下垫面条件下的CN值,并分析CN值与各影响因子的关系[6]。这些模型获得的结果较为精确,但有一定的局限性,针对不同的流域,由于水文状况和土壤条件的区别,这些方法所建立的CN值不能适应其他流域。
(2)模型参数改进。Singh和Mishra考虑蒸散发,并改进初损估计值方法,对大尺度的降雨进行估算[7-8]。Sahu等考虑雨强与前5日降雨量的关系,改进初损值[9]。樊登星在北京山区坡面研究土壤侵蚀时利用反算法算得不同土地利用下初损率λ,并将前期土壤含水量M作为新参数引入模型中, 发现改进后的新径流曲线模型(SCS-CN-MS)具有一定适用性[10]。王白陆根据数理统计原理,利用标准差来优化模型[11]。范营营等通过径流对有效降雨的积分改进模型[12]。参数的修正并未解决大尺度流域的地表径流问题。
本次研究区选定为陕西省榆林市绥德城的韭园沟流域,该流域面积为70.7 km2,测站控制面积达到了70 km2,两者几近吻合,因此可直接将该测站数据用于整个流域,同时该流域的资料齐全,易获得。韭园沟流域属于陕北地区,是黄土高原中心地带的典型代表,地势特点明显(北高南低,西高东低),水土流失严重。在该流域采用SCS-CN模型开展径流模拟与预报研究,对黄土高原区上进行水土流失预报、水土保持措施实施和非点源污染负荷估算有着重要意义。
1 资料与方法介绍 1.1 流域概况及数据韭园沟地处绥德城东北方向,是位于无定河左岸的一条支沟,全流域面积70.7 km2,韭园沟测站以上控制面积为70.1 km2。流域内丘陵起伏,沟壑纵横,主沟纵贯整个流域,全长达18 km,平均宽度为3.89 km。5 km以上的支沟有10条,1 km以上的支沟有68条,200 m以上的支沟有257条。沟壑密度5.34 km/km2。丘陵最上层为黄土层,其次是红土层,而再往下的就是三叠纪的沙岩层。沟底至峁顶相对高差100~200 m。韭园沟流域土地贫瘠,地形支离破碎,是典型的黄土高原丘陵沟壑区第一副区。
韭园沟流域年均降水量为450 mm,大部分的降水量集中在7—9月,年平均温度9.3 ℃,绝对最高温度39 ℃,最低温度-27 ℃,无霜期150~180 d,一年中西北风偏多,最大风力12.5 m/s。本研究共收集了韭园沟流域1954年至1968年之间的81场降雨及其径流数据(其中1955年缺测)。
1.2 模型介绍王英引入雨强因子来修正降雨量函数,结合黄土高原的地表径流大都为超渗产流形式,经过一系列的试验研究后发现修正后的降雨量正相关于最大30 min雨强,并给出了一个较为适合黄土地区的降雨量修正函数,通过试验证明该模型的预报精度很高[13]。降雨量的修正式如下:
| $ {{P}_{\text{a}}}=\left( Py{{I}_{30}}/I \right){{y}^{\beta }} $ | (1) |
式中:Pa为修正后降雨量(mm);I30为次降雨中最大30 min的雨强(mm/h);I为次降雨平均雨强(mm/h);β为降雨强度修正参数。
将式(1)与标准SCS-CN公式相结合,推出基于雨强的下列计算式:
| $ Q=\left\{ \begin{matrix} \frac{{{\left( P{{\left( {{I}_{30}}/\bar{I} \right)}^{\beta }}-\lambda S \right)}^{2}}}{P{{\left( {{I}_{30}}/\bar{I} \right)}^{\beta }}+\left( 1-\lambda \right)S},&P{{\left( {{I}_{30}}/\bar{I} \right)}^{\beta }}>{{I}_{\text{a}}} \\ 0,&P{{\left( {{I}_{30}}/\bar{I} \right)}^{\beta }}\le {{I}_{\text{a}}} \\ \end{matrix} \right. $ | (2) |
所谓反算法(Back Calculation,简称BC)即将标准SCS-CN方程反推,推出以Ia/S为结果的形式,而Ia/S就是初损率λ,反解出的计算式如下:
| $ \lambda =\left( 2P-Q-\sqrt{{{Q}^{2}}+4QS} \right)/(2S)~ $ | (3) |
周淑梅等在黄土丘陵沟壑区典型小流域SCS方法研究中对初损率的取值采用反算法和事件分析法优化初损,算得的结果均小于标准初损率0.2,但事件分析法的计算值略大于反算法,经过误差分析和图形拟合验证后采用反算法得到的结果为0.1[14]。樊登星利用改进径流曲线模型(SCS-CN-MS),通过反算法计算大量典型降雨径流事件中不同土地利用条件下的初始损失系数λ,引入前期土壤含水量到模型中,并结合前期降雨指数模型(API)来算得前5日降雨量,以确定前期的土壤水分;结果表明,改进后的径流曲线模型在北京山区有着较好的适用性[10]。
1.3.2 验证方法(1) Nash-Sutcliffe公式 纳什效率系数(Nash-Sutcliffe efficiency coefficient, 简称NSE)可用于水文模型的验证,用E来表示计算值(预测径流量)与实际值(实测径流量)的接近程度,公式如下:
| $ E=1-\sum\limits_{i=1}^{n}{{{\left( {{Q}_{i}}-Q_{i}^{*} \right)}^{2}}}/\sum\limits_{i=1}^{n}{{{\left( {{Q}_{i}}-\tilde{Q} \right)}^{2}}} $ | (4) |
式中:Qi为实测第i场降雨在流域面积上产生的径流深(mm);Qi*为计算获得的第i场降雨在流域面积上产生的径流深(mm);
(2) 线性回归方程分析 在Excel中模拟预测径流深(Y轴)与实测径流深(X轴)的趋势线并与直线Y=X作比较。
(3) 最小平方差 任意拟定参数,代入公式获得计算值,将实际值与计算值相减后再平方求和,最小值对应的参数就是所寻求的最优参数。目标函数如下:
| $ \text{LSE}=\sum\limits_{i=1}^{n}{{{\left( {{Q}_{i}}-Q_{i}^{*} \right)}^{2}}} $ | (5) |
CN值又称为径流曲线数,可反映地表产流的能力。SCS模型对CN值的精确度要求很高,该参数综合考虑了前期雨量、前期土壤湿度、土地类型、土壤水分下渗率等各个因素,故而在不同的流域所对应的CN值有着很大的区别,由此可见,标准SCS模型中如何精确地寻找出CN值极为重要。本文鉴于黄土高坡较为特殊的地形与气候,参考了符素华等[15]对CN值确定方法的研究方法(平均值法、中值法、算术平均法、S对数频率曲线法和渐近线法)。
通过符素华等的大量试验数据对5种方法的对比分析发现[15]:从纳什效率系数看,渐近线法有一定的优势;从合格率和相关系数R看,算术平均法更有一定依据性。综合比较这两种方法的适用范围、计算量大小等,得出采用算术平均法计算CN值相比于其他4种方法更为科学合理。
对51场长系列降雨径流实测数据进行计算分析获得标准CN值为76.61。韭园沟流域地处陕西省北部,接受日照时间充足,是中国日照高值区之一,年平均日照时长2 593.5~2 914.4 h。该流域地形错乱,表层覆盖土壤为易受侵蚀的黄绵土,前期土壤湿度较小,AMC等级被划分为Ⅰ级,对应的径流曲线数为58.8,即标准CN值。相应的潜在最大保持量为178.1 mm。
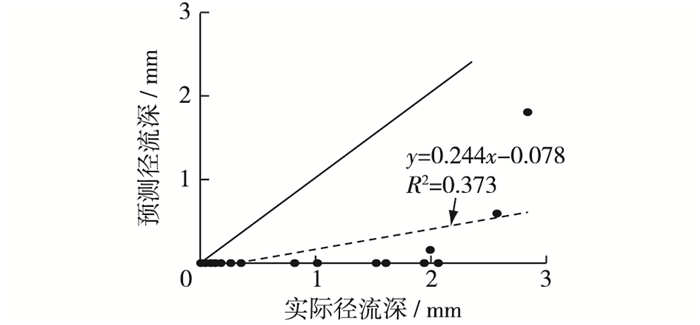
2.2 标准SCS模型验证将确定的标准CN值回代入标准SCS模型进行回归分析:选用1963年至1968年29场实测降雨数据,对参数率定后的标准模型进行验证(λ取为标准值0.2,S取178.1)(图 1)。模型验证发现,纳什效率系数为负,而这表明了实测值的平均值相对于模型的预报值在进行径流量估算时有着更好的效果。试验数据得到的趋势线斜率为0.244,截距为-0.079,明显可见预测值远小于实际值,结果对比见图 1。上述两种验证方法校验的结果不理想,归根结底,症结在于λ取0.2过大,使得大部分系列资料中的降水的初期损失量Ia大于降雨量P,导致预测径流量默认为0。在29组数据中,有24组的预测径流深为0,目前的SCS模型并不能准确预报径流,因此适当修正初损率λ变得尤为关键。
|
图 1 标准SCS模型实测值与径流值对比 Figure 1 Comparison of measured and predicted runoff values of standard SCS model |
国外学者Ponce,Hawkins等研究发现λ的取值一般在0~0.3,而Woodward也同样是认为λ取值小于0.2的概率高达90%。通过国内外学者们的大量研究也证实了50%左右的降雨事件初损率λ的取值范围为0.095~0.380[15]。
3 初损率λ的率定与优化 3.1 反算法优化模型参数及验证本次研究采用反算法,拟选定了韭园沟流域1954—1964年间的51场降雨事件。已知潜在最大保持量S为178.1 mm,结合51组P-Q数据并代入计算式(3),即可算得51组结果。将这一系列数据进行排序后取中值为0.075,即优化后的λ值取0.075。
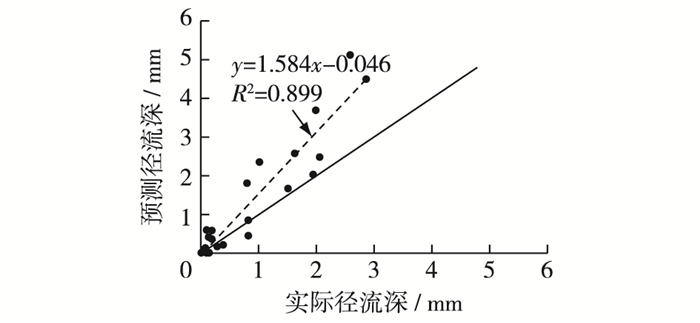
选定1963年至1968年29场实测降雨径流数据,代入初损率优化后的SCS模型进行模型检验,λ取为标准值0.075,CN值取58.8,S取178.1。利用纳什公式进行效率验证,发现算得纳什效率系数E为0.208,尽管改进后的模型效率已变为正,但是这样的模型预报精度仍需进一步优化。将实测径流深与预测径流深拟定回归方程,分析结果:斜率为1.585,截距为-0.046,明显看出预测值已超出于实际值;相关系数的平方R2达到了0.899,远高于之前的0.374,说明实测值与预测值的相关程度有了很大的提高。对比结果见图 2。综上两种验证方法校验的结果,反算法优化参数使得模型精度有所提高,但模型效率E还待提高。
|
图 2 反算法改进SCS模型实测值与径流值对比 Figure 2 Comparison of measured and predicted runoff values of improved SCS model by black calculation |
LSE(最小平方差)是把n场降雨径流资料里的实测值与预测值的差值平方后再累积而得。LSE愈小,则预测值愈接近实测值,模型的模拟度则愈高。利用MATLAB编程过程分为两个部分:①计算出每个初损率λ下每场降雨的径流预测值Q(i)以及对应这一系列数据的一个最小平方差LSE;②找出所有LSE中最小的值,并给出对应的λ。
本研究以LSE作为目标函数,以找到当LSE最小时对应的参数λ,该λ即为符合韭园沟流域的最优初损率λ。将流域1954—1964年间的51场实测降雨径流资料导入MATLAB,并转成mat文件。通过MATLAB软件粒子群优化算法,输出λ为0.13,LSE为30.04。
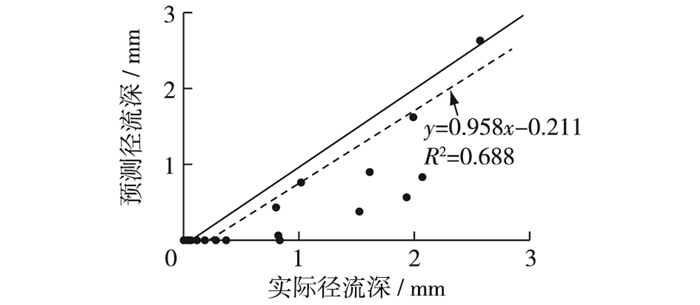
3.2.2 利用MATLAB优化后SCS模型的验证选定1963年至1968年29场实测降雨径流数据,代入初损率优化后的SCS模型中,λ取为标准值0.13。利用纳什公式进行效率验证,发现算得纳什效率系数E为0.504,通过采用MATLAB优化初损率后,模型的纳什有效系数与上次优化后相比,又有了明显的提高,此时的模型已具有一定的预报径流能力。将实测径流深与预测径流深拟定回归方程,分析结果得斜率为0.958,截距为-0.212,这表明预测径流深已非常接近于实际径流深;而相关系数的平方R2虽然有所减小,但这对模型整体精度并没有多大的影响。对比结果见图 3。综上两种验证方法校验的结果,采用MATLAB粒子群算法优化参数使得模型精度提高很多。在黄土高原小流域或小区域中,针对不同地区的降雨、土地类型、土壤质地、植被覆盖等因子各有不同,利用SCS模型估算径流时,需要根据当地适应性评价,重新拟定初损率λ。
|
图 3 利用MATLAB粒子群优化算法改进SCS模型实测值与预报值对比 Figure 3 Comparison of measured and predicted runoff values of improved SCS model by using MATLAB particle swarm optimization algorithm |
标准SCS-CN模型在预报径流时,因λ的率定不够精确,模型效率为负,其次未考虑前期土壤湿度在黄土高坡上对模型的影响。因此在资料充足的前提下,需探讨黄土高原丘陵沟壑区的符合该模型的前期土壤湿度等级划分标准;而通过反算法改进的SCS方法,模型效率提高到0.208,但其预报的径流深却已经高于实际的径流深;最后通过MATLAB来改进SCS-CN模型对小降水产流事件的预报能力显著提高,回归方程的斜率也已无限接近1,但模型效率E为0.504,相比之前的方法已经提高很多,但这还不是最理想的。3种径流模型的对比分析见表 1。
| 表 1 韭园沟流域3种径流预报模型的分析比较 Table 1 Comparison of three runoff forecast models for Jiuyuangou watershed |
陕西黄土高原地区属于干旱、半干旱气候带,地下水埋深较深,植被稀疏,水土流失严重,气候较干旱,降水集中且少,地面产流主要以超渗产流的形式存在。为了提高SCS模型精度,需引入雨强因子来修正降雨量函数。从20世纪50年代开始,对于黄土高坡上的降雨特征的研究就已经开始。吴发启等 研究发现各类组合指标P30I30与对黄土高原缓坡耕地上的降雨、产流、产沙的表征更为恰当。
选用1954年至1963年的韭园沟重点雨量筒汛期降水量摘录表上的44场符合要求的降雨。将重点雨量筒汛期降水量摘录表的小时段及其相应的降水量采用雨强过程线的积分,可由逐时段的雨量沿时程累加求得;各时段的雨量可由累积雨量过程线差分得到,除以相应的时段长,得各时段雨强,从而绘出降雨强度过程线。在累积雨量过程线上取时段长度为30 min,找到在这些时段中降雨量增加量最大的一段,即为I30。采用累积雨量过程线法转化出I30。
4.1 利用MATLAB粒子群优化算法改进函数 4.1.1 MATLAB粒子群优化算法率定λ, β选择1954年至1963年的44组数据,其中包括雨量、径流深、最大30 min雨强和平均雨强。以最小平方差作为目标函数,将雨量、径流深和Ia/ 这3组数据导入MATLAB转化成mat文件。通过粒子群优化算法,算出最优初损率λ为0.10,雨强修正参数β为-0.084,LSE为25.546。
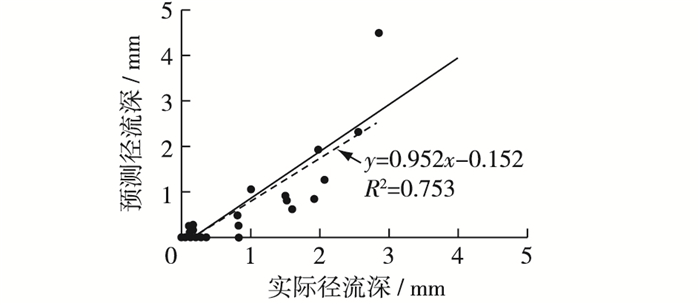
4.1.2 改进后函数的验证基于雨强因子修正降雨量后改进的SCS模型,在各个方面都要优于之前仅仅改进了初损率λ的那些模型。选定1963年至1968年33场符合要求实测降雨径流数据,代入基于雨强因子修正降雨量后改进的SCS模型中,λ取为标准值0.10,雨强修正系数β为0.084。利用纳什公式进行效率验证,发现算得纳什效率系数E提高到0.652,通过采用MATLAB粒子群优化算法优化初损率和雨强修正系数后,模型的纳什有效系数与上次优化后相比,又有了明显的提高,此时的模型预报径流的能力已经成熟。将实测径流深与预测径流深拟定回归方程,分析结果得:斜率为0.953,截距为-0.153,回归方程的斜率基本已接近1,而相关系数的平方R2相比于仅优化λ时也有了一定提升,此时可以认为预报径流量等于实际径流量。对比结果见图 4。无论是纳什公式,还是回归方程分析,这两种验证方法对改进后的新函数的验证效果都很好,改进后的SCS模型函数在黄土高原地区的径流深预报精度很高。
|
图 4 基于雨强改进后模型径流实测值与预报值的对比 Figure 4 Comparison of measured and predicted values of runoff based on improved rainfall intensity |
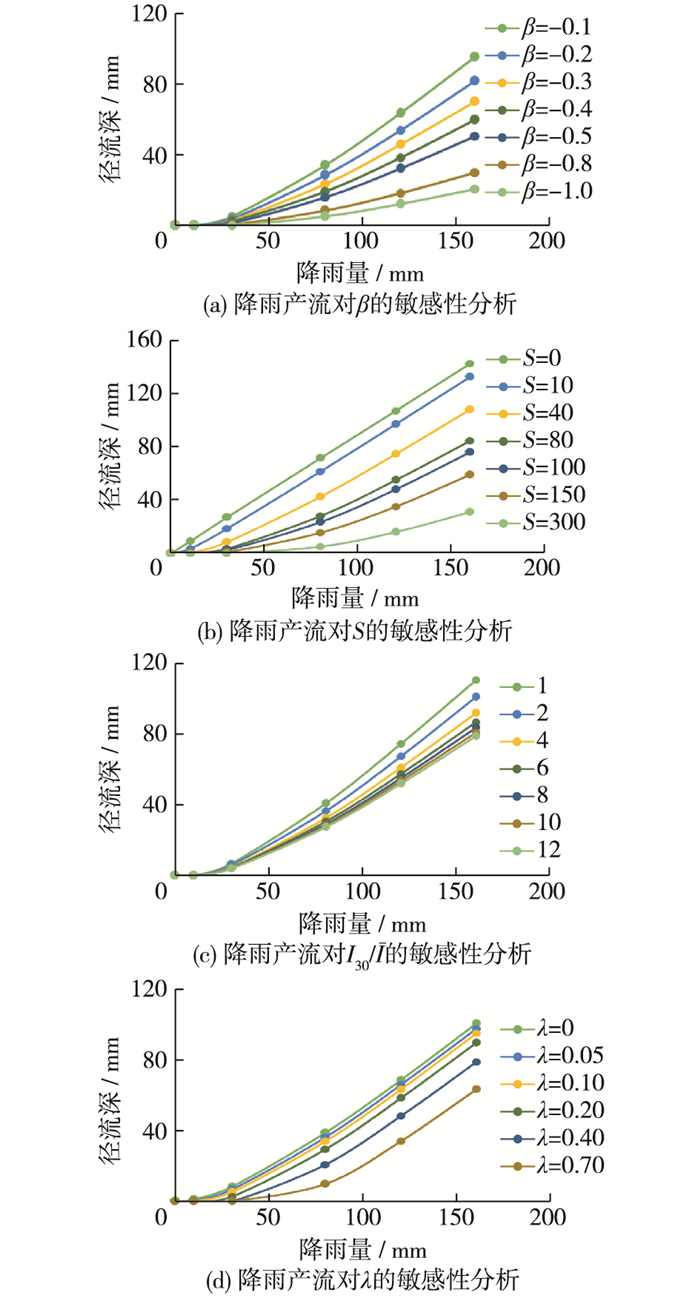
假定S=60,λ=0.1,I30/I=3,改变β的取值,在每个β值下,降雨的取值范围在0~160 mm,径流深随着降雨量的变化而变化,最终形成一簇光滑曲线。在β分别为-0.1,-0.2,-0.3,-0.4,-0.5,-0.8和-1.0时,得到的径流曲线见图 5(a):在相同降雨量的情况下,随着β值的增大,地表产流径流深也随之变大。
|
图 5 降雨产流的敏感性分析 Figure 5 Sensitivity analysis of rainfall runoff |
假定λ=0.1,β=-0.1,I30/I=3,改变S的取值,分别为0,10,40,80,100,150和300 mm,绘出在每个S值下的降水径流曲线(见图 5(b))。由图 5(b)可得:在相同降雨量的情况下,随着S值的增大,地表产流径流深也随之变大;当S=0 mm时,初损量Ia为0,此时径流深与降雨量呈一次线性关系,并且该直线经过坐标原点(0, 0);随着S的增大,径流深变化率也越来越小。
4.2.3 降雨产流对I30/I的敏感性假定S=60,β=-0.1,λ=0.1的前提下,改变I30/I的取值为1,2,4,6,8,10和12,绘出径流深关于降雨量的一簇曲线(见图 5(c))。由图 5(c)可得:在相同降雨量的情况下,随着最大30 min雨强与平均雨强两者的比值的增大,地表产流量愈来愈少;两者比值越小,径流量随降雨量的变化率却越大,反之则越小。
4.2.4 降雨产流对初损率λ的敏感性假定S=60,β=-0.1,I30/I=3的前提下,改变初损率λ的取值分别为0,0.05,0.10,0.20,0.40和0.70,绘制径流深关于降雨量的一簇光滑曲线(见图 5(d))。由图 5(d)可得:在相同降雨量的情况下,随着初损率λ的增大,地表径流逐渐减小;在小降雨事件中,随着初损率的增大,地表径流为0的可能性也就越大。
5 结语径流曲线法所含参数少,便于计算,适用于缺乏资料的地区,本次研究将该方法用于黄土高原地区韭园沟流域,通过对SCS-CN模型的改进,得到如下结论:
(1) 由于前期土壤湿润程度、土壤下渗率等数据获得困难,本研究采用算术平均法来确定最终标准CN值为58.8,但由于默认标准初损率0.2过大,使得大部分的小降雨事件中地表产流预报值小于实际值。尝试使用反算法来优化初损率,确定λ为0.075,但此时模型效率只有0.208。采用MATLAB软件结合粒子群算法来进一步优化初损率,结果λ为0.13,模型效率为0.504,相比于反算法提高了142%。
(2) 考虑到黄土高原上的降雨形式一般以短历时、高强度形式,而标准SCS-CN模型并未考虑到这一点,函数中并不存在雨强参数,故参考王英等在黄土丘陵沟壑区引入雨强因子修正降雨量函数之后,得到韭园沟流域的最终SCS模型,其中β为-0.084,λ为0.1。
模型效率为0.652,决定系数为0.753,利用雨强修正函数后的SCS模型相比于标准SCS模型,决定系数R2和模型效率E分别提高了101%和534%。
对改进后的降雨径流函数进行敏感性分析发现:①在相同降雨量的情况下,随着β值的增大,地表产流径流深也随之变大;在参数β变幅为±10%的前提下,敏感性系数可达到1.68,影响显著。②在相同降雨量的情况下,随着S值的增大,地表产流径流深也随之变大;当S=0时,初损量Ia为0,此时径流深与降雨量呈一次线性关系,并且该直线经过坐标原点(0, 0);当S=300时,径流深随降雨的变化很小;随着S的增大,径流深的变化率变小;一般CN取值为30~100,所以潜在最大保持量S取值范围很大,敏感系数在其变化范围内并不稳定。③在相同降雨量的情况下,随着最大30 min雨强与平均雨强两者比值的增大,地表产流量愈来愈少;两者比值越小,径流量随降雨量的变化率却越大,反之则越小;该参数对降雨产流影响较小。④在相同降雨量的情况下,随着初损率λ的增大,地表径流逐渐减小;在小降雨事件中,随着初损率的增大,地表径流为0的可能性也就越大。
| [1] |
王红艳, 张志强, 查同刚, 等. 径流曲线数(SCS-CN)模型估算黄土高原小流域场降雨径流的改进[J]. 北京林业大学学报, 2016, 38(8): 71-79. ( WANG Hongyan, ZHANG Zhiqiang, ZHA Tonggang, et al. Improvement of rainfall runoff in small watershed of Loess Plateau by using SCS-CN model[J]. Journal of Beijing Forestry University, 2016, 38(8): 71-79. (in Chinese)) |
| [2] |
AUERSWALD K, HAIDER J. Runoff curve numbers for small grain under german cropping conditions[J]. Journal of Environmental Management, 1996, 47(3): 223-228. DOI:10.1006/jema.1996.0048 |
| [3] |
MANKIN K R, KOELLIKER J K, BHUYAN S J. Watershed-scale AMC selection for hydrologic model[J]. Transactions of the ASAE, 2003, 46(2): 303-310. |
| [4] |
张钰娴, 穆兴民, 王飞. 径流曲线数模型(SCS-CN)参数λ在黄土丘陵区的率定[J]. 干旱地区农业研究, 2008, 26(5): 124-128. ( ZHANG Yuxian, MU Xingmin, WANG Fei. Calibration and validation to parameter λ of soil conservation service curve number method in hilly region of the Loess Plateau[J]. Agricultural Research in the Arid Areas, 2008, 26(5): 124-128. (in Chinese)) |
| [5] |
李常斌, 秦将为, 李金标. 计算CN值及其在黄土高原典型流域降雨-径流模拟中的应用[J]. 干旱区资源与环境, 2008, 22(8): 67-70. ( LI Changbin, QIN Jiangwei, LI Jinbiao. Application of computational curve number to precipitation-runoff simulation in a typical watershed in Chinese Loess Plateau[J]. Journal of Arid Land Resources and Environment, 2008, 22(8): 67-70. (in Chinese)) |
| [6] |
罗利芳, 张科利, 符素华. 径流曲线数法在黄土高原地表径流量计算中的应用[J]. 水土保持通报, 2002, 22(3): 58-61. ( LUO Lifang, ZHANG Keli, FU Suhua. Application of runoff curve number method on Loess Plateau[J]. Bulletin of Soil and Water Conservation, 2002, 22(3): 58-61. (in Chinese)) |
| [7] |
MISHRA S K, JAIN M K, BHUNYA P K, et al. Field applicability of the SCS-CN based Mishra-Singh general model and its variants[J]. Water Resources Management, 2005, 19(1): 37-62. DOI:10.1007/s11269-005-1076-3 |
| [8] |
MISHRA S K, PANDEY R P, JAIN M K, et al. A rain duration and modified AMC-dependent SCS-CN procedure for long duration rainfall-runoff events[J]. Water Resources Management, 2008, 22(7): 861-876. DOI:10.1007/s11269-007-9196-6 |
| [9] |
SAHU R K, MISHRA S K, ELODHO T I, et al. A modification to the initial abstraction in the existing SCS-CN methodology incorporating storm duration and antecedent rainfall[J]. Recent Advances in Water Resources Development and Management, 2005, 697-704. |
| [10] |
樊登星. 北京山区坡面土壤侵蚀响应特征及模型模拟研究[D]. 北京: 北京林业大学, 2014. (FAN Dengxing. Study on soil erosion response characteristics and model simulation of slope in Beijing mountain area[D]. Beijing: Beijing Forestry University, 2014. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10022-1014324730.htm
|
| [11] |
王白陆. SCS产流模型的改进[J]. 人民黄河, 2005, 27(5): 24-26. ( WANG Bailu. Improvement of SCS runoff model[J]. Yellow River, 2005, 27(5): 24-26. (in Chinese)) |
| [12] |
范营营, 胡铁松. SCS-CN模型的改进及在澎家滩流域的应用[J]. 中国农村水利水电, 2009(12): 11-14. ( FAN Yingying, HU Tiesong. The improvement of SCS-CN model and its application in Pengjiatan watershed[J]. China Rural Water and Hydropower, 2009(12): 11-14. (in Chinese)) |
| [13] |
王英. 径流曲线法(SCS-CN)的改进及其在黄土高原的应用[D]. 北京: 中国科学院研究生院(教育部水土保持与生态环境研究中心), 2008. (WANG Ying. Improvement of runoff curve method and its application in Loess Plateau[D]. Beijing: Graduate School of Chinese Academy of Sciences(Soil and Water Conservation and Ecological Environment Research Center, Ministry of Education), 2008. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-80129-2010210138.htm
|
| [14] |
周淑梅, 雷廷武. 黄土丘陵沟壑区典型小流域SCS-CN方法初损率取值研究[J]. 中国农业科学, 2011, 44(20): 4240-4247. ( ZHOU Shumei, LEI Tingwu. Calibration of SCS-CN initial abstraction ratio of a typical small watershed in the loess Hilly-Gully region[J]. Scientia Agricultura Sinca, 2011, 44(20): 4240-4247. (in Chinese)) |
| [15] |
符素华, 王向亮, 王红叶, 等. SCS-CN径流模型中CN值确定方法研究[J]. 干旱区地理, 2012, 35(3): 415-421. ( FU Suhua, WANG Xiangliang, WANG Hongye, et al. Method of determining CN value in the SCS-CN method[J]. Arid Land Geography, 2012, 35(3): 415-421. (in Chinese)) |
| [16] |
吴发启, 赵晓光, 刘秉正, 等. 黄土高原南部缓坡耕地降雨与侵蚀的关系[J]. 水土保持研究, 1999, 6(2): 53-60. ( WU Faqi, ZHAO Xiaoguang, LIU Bingzheng, et al. Relation between rainfall and soil erosion in the gentle slope land in the south part of loess plateau[J]. Research of Soil and Water Conservation, 1999, 6(2): 53-60. (in Chinese)) |
2. College of Water Resources and Architectural Engineering, Northwest Agriculture and Forestry University, Yangling 712100, China
 2018
2018 
