2. 南京水利科学研究院 港口航道泥沙工程交通行业重点实验室, 江苏 南京 210029
丁坝是传统的整治建筑物之一,通常用于疏导河道与保护河岸。丁坝的修建,势必造成原水流能量与动量的改变,而水流具有丁坝附近水流流速及水深以平衡丁坝作用力的能力。丁坝的作用力即为丁坝水流力,关系到丁坝结构的整体稳定性。
丁坝水流力通常采用拖曳力的形式表示[1],与Evett [2]公式形式类似。李社生[3]通过物理水槽试验主要以锁坝形式对齿型构件混合堤在不同流速、水深、堤高、堤长及流向条件时水流力进行研究。贝建忠等[4]通过数值模拟以锁坝形式对齿形构件在不同水流条件下进行了模拟研究。闫杰超等[5]通过数值模拟以丁坝形式对该齿形构件在不同流速、水深及坝长条件下水流力特性进行了研究,并对构件水流力的分布特性进行了探讨研究。但不同的水流力公式仅水流力系数不同。Azinfar等[6]通过研究淹没丁坝发现水流力系数并非常数,它与坝高、坝长、水深、流速以及丁坝形状等因素密切相关;还通过分析Oak淹没丁坝试验数据得到了与丁坝横纵比(坝高与坝长比值)、相对坝长、淹没度和弗劳德数相关的水流力系数公式,公式表明,水流力系数随着横纵比的增大而减小,随着相对坝长的增加而增加,随着淹没度的增加而减小,随着弗劳德数的增加而减小[7-8]。Azinfar[9]通过物理试验研究了淹没丁坝水流力系数与淹没度和相对坝长的关系,研究表明水流力系数随着相对坝长的增加而增加,随着淹没度的增加而减小。而后,Azinfar和Kells [10]通过物理试验研究了丁坝阻水比对水流力系数的影响。
目前,长江南京以下12.5 m深水航道整治工程引入了该新型淹没丁坝,但鲜有对其水流力及水流力系数进行系统研究的。因此,本文通过建立三维水动力模型,对新型淹没丁坝的水流力及水流力系数进行基础性的研究。
1 模型研究 1.1 物理模型研究 1.1.1 物理模型试验物理模型试验在国家重点实验室南京水利科学研究院长江下游模型试验厅完成。物理水槽根据数值水槽尺寸、试验厅和水流循环系统的供水能力等,确定为长40.0 m,宽3.5 m,高0.5 m,底面坡度为1/1 500,模型比尺为1:50。在水槽中断选取长为37 m的一段作为试验段,首部留2 m,尾部留1 m作为过渡段。试验水槽由量水堰、消能静水段、过渡段、试验段及尾水段组成。
1.1.2 水流力试验方法及结果丁坝水流总力测量采用南京水利科学研究院研发的总力(拉压力)传感器测量,试验采样频率设为20 Hz,采样时间为每次20 s(图 1)。为保证试验结果的可靠性,每组试验数据采集4~7次,并取其均值作为总力测量结果(表 1)。

|
图 1 齿形结构丁坝水流力测量布置示意 Figure 1 Sketch of the measureing layout of tooth-shaped spur dike |
| 表 1 物理试验水流力测量 Table 1 Measurement of flow force of physical experiment |
物理试验前首先对拟定的各种水流条件进行率定,得出上游端量水堰的读数及下游端尾门的量水堰读数;在水槽无水的情况下铺设碎石基床,将齿形构件放置在基床上,按照试验组次铺设齿形构件个数;将试验构件与测力设备连接好,并将其底部悬空吊挂在位于水槽侧墙的横架上,以保证测力构件处于悬浮状态,同时,用金属螺杆将总力传感器与铁架固定,以使测力仪的受力与作用于齿形构件上的水流力相平衡。在安装好测力构件与测力仪器之后,按照试验组次开始放水,放水的过程中将水槽尾门关闭,以保证试验断面的上下游水位同时抬升;当水槽尾门水位达到试验水位时,停止放水,待到水面稳定,在水流静定条件下对测力仪器进行调零;测力仪器调零之后,按各试验组次的水流条件调节上游调节量水堰和下游调节尾门进行试验,待水位平稳之后开始采集测力数据。对一定坝长中多个齿形构件依次采用上述方法进行水流力测量,最后求和得到整个丁坝的水流力。
1.2 数学模型 1.2.1 模型建立新型淹没丁坝的齿形构件采用混凝土预制而成,设计为“丰”字型对称形块体,两侧各有对称的三道横齿,称为三道横齿形构件。实际工程中构件长8.65 m,宽6.50 m,坝高8.50 m,由基床以上部分与基床部分组成,分别高7.0 m和1.5 m。基床由10~100 kg块石铺设,两侧坡度为1:1,坝身两侧均由200~300 kg棱体块石铺设,坡度为1:2。本文通过模型概化采用ANSYS Fluent对数值模型进行构建,其中,齿形结构模型与实际工程中齿形结构的尺寸一致,流体区域尺寸的确定则综合考虑了物理试验场地的实际条件、丁坝流场结构的完整性以及实际计算机的性能等,最终确定流体区域总长700 m,宽175 m,其中坝前长300 m,坝后长400 m。模型如图 2所示。

|
图 2 模型建立示意 Figure 2 Sketch of model building |
本文数值模拟利用有限体积法求解连续性方程和雷诺时均N-S方程,并采用RNG k-ε湍流模型来封闭方程组,自由液面则采用VOF法求解单元液相体积分数确定。由于流动为非定常流,故采用显式VOF方案,近壁流动采用标准的壁面函数法。方程离散时压力差值采用Body Force Weighted格式,湍动能与耗散率的离散采用一阶迎风格式,压力速度耦合采用PISO算法。收敛标准为计算各变量残差小于0.000 01。具体网格划分、模拟方法及模型验证已在文献[5]中详细介绍,本文将不再赘述。
1.2.3 数值模拟组次设置为深入系统地对新型结构丁坝进行研究,本文从不同水深、流速及坝长条件出发,对新型结构丁坝水动力及水流力特性展开研究,其中水深h为13~16 m,流速V为1.5~3.0 m/s,坝长b为8.7~43.3 m。模拟组次共17组,具体条件如表 2所示。
| 表 2 数值模拟组次 Table 2 Groups of numerical simulation |
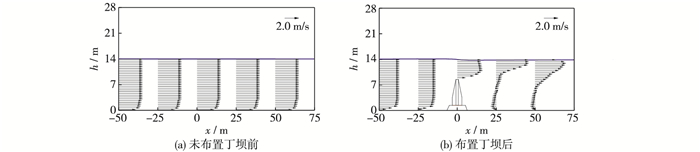
如图 3(a)所示,以数模组次3为例,当数值水槽无丁坝布置时,模拟的纵断面流速分布曲线呈对数律型,外部湍流区流速分布均匀。如图 3(b)所示,水槽布置丁坝后,当水流行近至丁坝断面,水平流速逐渐减小,并伴随着水位壅高;当水流经过坝顶时,流速增加明显;坝后出现一定范围的流域的表底层流速方向相反,且表层流速多大于底层流速,水流呈面流式流态。
|
图 3 布置丁坝前后速度矢量变化 Figure 3 Change of velocity vector with and whthout submerged spur dike |
如图 4所示,以来流流速V=2.0 m/s,h=14 m,齿形构件个数分别为2~5块单侧铺丁坝为例,由于丁坝的阻水作用,随着水流动能部分或全部转化为势能,丁坝与布置岸之间流速减小明显;当水流绕至坝头附近,水流快速下泄,流速则明显增大;坝后水流由于受到丁坝的掩护作用,流速变化剧烈,呈三维紊动流态,且坝后较远处流速基本恢复为来流速度V=2.0 m/s。同时,随着丁坝坝长或齿形构件个数的增加,丁坝对水流的影响范围逐渐增大,坝前流速随着坝长的增加而相应减小,坝后流速亦随坝长的增加而相应减小。

|
图 4 不同坝长条件下自由表面流速分布 Figure 4 Distribution of flow velocity of free surface with different lengths of submerged spur dike |
如图 5所示,以来流流速V=2.0 m/s,h=14 m,齿形构件个数分别为2~5块单侧铺丁坝为例,当河道布置丁坝后,由于丁坝的阻水作用,水流在丁坝与布置岸之间形成壅水区,坝前断面水深从坝根到坝头逐渐减小,并向水槽对岸水面渐趋平缓,当坝前水流绕至坝头时快速下泄,水深减小明显;而坝后水流由于受到丁坝的掩护作用,坝前壅高水流漫过坝顶形成跌水,水流呈三维紊动流态,且坝后较远距离水深逐渐恢复为来流条件水深14m。同时,随着丁坝坝长或齿形构件个数的增加,丁坝对水流的影响范围逐渐增大,坝前壅水高度随着坝长的增加而相应增大,坝后跌水值亦随坝长的增加而相应增大。

|
图 5 不同坝长条件下水深分布规律 Figure 5 Distribution law of water depth with different lengths of submerged spur dike |
根据不同来流流速、水深与坝长条件下共17个组次的模拟结果,首先分析来流流速、坝长及水深对新型淹没丁坝水流力的影响。
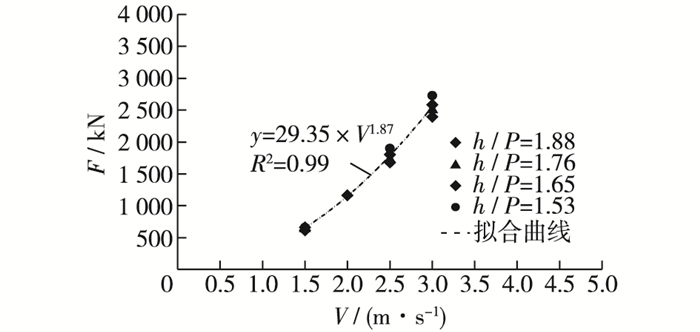
如图 6所示,淹没丁坝水流力大小与来流流速关系密切,且随着流速的增加而增加;在相同坝长与来流流速条件下,淹没丁坝水流力大小随着水深的增加呈减小的趋势,这是由于随着水深增加,丁坝上下游水面波动减小,导致丁坝水流力减小的缘故。由图中拟合曲线可知,水流力与来流流速呈二次方关系,这与文献[6, 8]对丁坝或者潜堤水流力随流速变化规律的研究成果一致。
|
图 6 丁坝水流力随流速变化的响应关系 Figure 6 Responding relationship of flow force of submerged spur dike varying with flow velocity |
如图 7所示,随着丁坝坝长的增加,3种坝型丁坝所受的水流力逐渐增加。由于丁坝坝长的增加,过流断面面积减小,丁坝对水流的压缩加剧,导致丁坝所受水流力增大;由于3道横齿形丁坝与两道横齿形丁坝结构类似,差别在于横齿个数的不同,因此,3道横齿形丁坝的水流力与李社生[3]对两道横齿形丁坝的水流力随坝长变化的研究结果一致,本文3道横齿形丁坝的水流力模拟结果略大于两道横齿形丁坝的水流力,其原因可归于两种齿形丁坝的结构差异;而从Azinfar[9]研究矩形平板丁坝的水流力随坝长变化趋势来看,相同坝长条件下,矩形平板丁坝的水流力明显大于另外两种结构丁坝的水流力,Azinfar[7]研究分析Oak[8]对矩形平板丁坝与三角形丁坝试验结果发现三角形丁坝由于坡度的存在,其水流力明显小于矩形平板丁坝的水流力,因此,本文研究丁坝基床及其坡度的存在对水流的阻挡作用起到抑制作用,其坝型相对安全。

|
图 7 丁坝水流力随坝长变化的响应关系曲线 Figure 7 Responding relationship of flow force of submerged spur dike varying with its length |
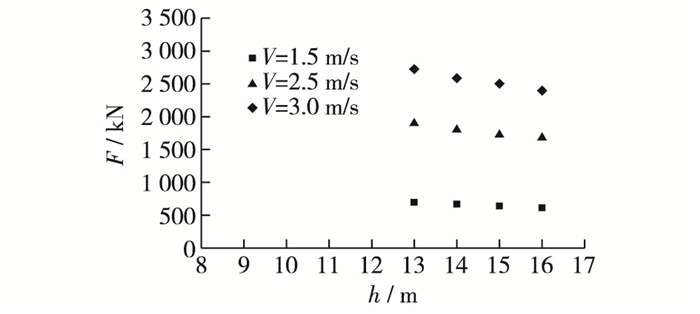
如图 8所示,随着水深的增加,淹没丁坝水流力逐渐减小。由于水深的增加,淹没丁坝上下游水面波动减缓,水面坡降减小,同时坝头及坝后紊动减弱,导致水流力减小,因此,增加水深或者降低丁坝坝顶高程可减小水流对丁坝的作用。由图 8亦可见,随着流速的增加,丁坝水流力增加明显,这也说明流速是丁坝水流力最主要的影响因素;同时,从丁坝水流力随水深的变化趋势来看,水深对水流力的影响小于坝长与流速的影响,且随着水深继续增加,其水流力将趋于常数或略微减小。
|
图 8 水流力与水深变化的关系 Figure 8 Relationship between flow force of submerged spur dike and water depth |
通常采用类似Evett等[2]的计算式表达水流力:
| $ {{F}_{\text{D}}}=\frac{1}{2}\rho {{C}_{\text{D}}}A{{V}^{2}} $ | (1) |
式中:FD为水流力;ρ为水的密度;CD为水流力系数;A为丁坝迎流面积;V为来流流速或坝后水流恢复段平均流速。
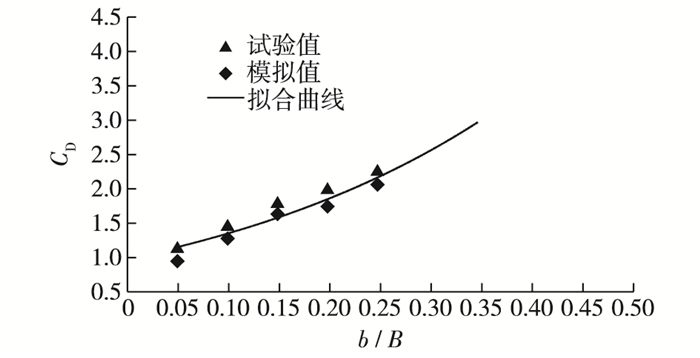
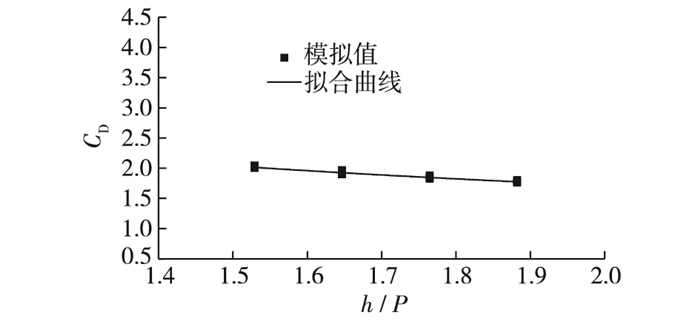
由式(1)可知,丁坝水流力求解的关键在于水流力系数CD的计算。丁坝水流力系数的大小通常由相对坝长、淹没度以及丁坝形状决定。相对坝长表示丁坝对河道或渠道的约束作用,通常采用坝长b与河宽B的比值表示相对坝长b/B。淹没度表示水流对丁坝的淹没程度,通常采用坝顶水深h与坝高P的比值表示淹没度h/P。丁坝形状对水流力系数的影响可用形状系数Δ表示,通常被视为常数项处理。因此,为了计算丁坝水流力系数,通过对模拟结果进行分析,采用控制变量法分别得到CD与相对坝长b/B、淹没度h/P的响应关系曲线如图 9与图 10所示。
|
图 9 丁坝水流力系数与相对坝长的关系(h/P=1.65) Figure 9 Relationship between flow force coefficient and relative length of submerged spur dike (h/P=1.65) |
|
图 10 丁坝水流力系数与淹没度的关系(b/B=0.25) Figure 10 Relationship between flow force coefficient and submerged ratio of submerged spur dike (b/B=0.25) |
在淹没度h/P一定的条件下,淹没丁坝水流力系数CD随相对坝长b/B的增加而增加。李社生[8]通过物理试验对齿形与半圆形潜堤水流力系数研究得出水流力系数与相对堤长呈指数函数关系,且随着相对堤长的增加而增加。Azinfar[9]研究认为随着相对坝长的增加,水流力系数相应增加,且在水深较低的情况下增加更加明显,而在相对坝长b/B一定的条件下,丁坝水流力系数CD随淹没度h/P的增加而减小。Yossef[11]与Van broekhoven[12]通过研究得出随着淹没度增加,淹没丁坝水流力系数相应减小。综合分析研究上述成果,得到水流力系数的拟合公式:
| $ {{C}_{\text{D}}}=1.24\text{exp}\left( 3.17b/B \right){{\left( h/P \right)}^{-0.605}} $ | (2) |
为了进一步分析相对坝长b/B、淹没度h/P与水流力系数CD之间的敏感性影响,将水流力系数函数定义为:
| $ {{C}_{\text{D}}}={{\varphi }_{1}}{{\varphi }_{2}} $ | (3) |
| $ {{\varphi }_{1}}={{f}_{1}}(b/B)~ $ | (4) |
| $ {{\varphi }_{2}}={{f}_{2}}(h/P) $ | (5) |
为了单独分析相对坝长b/B、淹没度h/P对水流力系数CD的影响,通过建立如下函数式将相对坝长b/B与淹没度h/P从水流力系数CD中分离出来进行分析。
| $ {{\varphi }_{1}}=\frac{{{C}_{\text{D}}}}{1.24{{\left( \frac{h}{P} \right)}^{-0.61}}} $ | (6) |
| $ {{\varphi }_{2}}=\frac{{{C}_{\text{D}}}}{1.24\text{exp}\left( 3.17\frac{b}{B} \right)~} $ | (7) |
式(6)与(7)允许单独分析一个变量对水流力系数的影响,得到不同因素与水流力系数的敏感性关系。
图 11为φ1随b/B变化关系曲线,曲线关系可用幂指数函数表示为
| $ {{\varphi }_{1}}=3.63{{\left( b/B \right)}^{0.38}} $ | (8) |

|
图 11 φ1随b/B变化响应关系 Figure 11 Relationship between φ1 and b/B |
Shaw[13]通过研究输水隧道里侧墙对平板拖曳力系数的影响关系发现,平板拖曳力系数与开孔率存在幂指数函数关系。由图 11可知,首先,当相对坝长b/B或者坝长b趋近于零时,意味着渠道或河道将不受丁坝的影响,此时φ1接近零;当相对坝长b/B趋近于1或者坝长b趋近于河宽B时,φ1将有最大值。其次,随着b/B增大,φ1呈现增大的趋势。Azinfar[6]通过研究1-b/B对水流力系数的影响发现当b/B接近0时,意味着丁坝不存在,其函数值φ2接近1,同时,其函数值φ2随着开孔率1-b/B的增加而减小。
如图 12所示,水流力系数随着淹没度的增加而减小。由于随着水深增加,丁坝上下游自由液面波动减小,丁坝水流力则相应减少。通过对数据点进行外部预测发现,当淹没度h/P趋近于2.0时,φ2值趋于常数,表示此时淹没度对水流力系数没有影响或影响很小。因此,φ2的函数关系可以表示为:
| $ {{\varphi }_{2}}=\text{ln}{{\left( {{h}_{2}}/P \right)}^{-0.57}}+1 $ | (9) |

|
图 12 φ2随h/P变化响应关系 Figure 12 Relationship between φ2 and h/P |
本文通过流体计算软件Fluent建立了三维数值模型,并结合物理水槽试验与理论分析的方法,对新型齿形结构丁坝在不同水流条件下的水动力特性及水流力特性进行研究,得到以下结论:
(1) 丁坝水流力与来流流速、坝长与水深响应关系密切。当流速增加时,水流力相应增加,且水流力与流速成二次幂关系;当坝长增加时,丁坝水流力也相应增加;但当水深增加时,丁坝水流力相应减小。
(2) 新型淹没丁坝水流力系数随着相对坝长的增加而增加,随着淹没度的增加而减小。
(3) 为分析无量纲数相对坝长与淹没度分别对水流力系数的敏感性,通过独立化分析方法,发现随着b/B增大,φ1呈增大趋势,当相对坝长b/B趋近于1时,φ1将有最大值;随着h/P增大,φ2呈减小趋势,当淹没度h/P趋近于2.0时,φ2值趋于常数,表示此时淹没度对水流力系数没有影响或影响很小;φ1随着b/B变化的敏感性大于φ2随着h/P变化的敏感性,相对坝长对水流力系数的影响大于淹没度。
| [1] |
AYA S, FUJITA I, MIYAWAKI N. 2-D Models for flows in the river with submerged groins[C]//Managing Water: Coping with Scarcity and Abundance, 2011: 829-834.
|
| [2] |
EVETT J. Fundamentals of fluid mechanics[M]. USA: McGraw-Hill College, 1987.
|
| [3] |
李社生. 航道整治建筑物新型堤身水流力试验研究[D]. 南京: 河海大学, 2014. (LI Shesheng. The experimental research of new structure's hydrodynamic of waterway remediation[D]. Nanjing: Hohai University, 2014. (in Chinese))
|
| [4] |
贝建忠, 孙克俐, 李元音, 等. 基于CFX的齿型构件混合堤翻坝水流力分析[J]. 港工技术, 2017, 54(1): 7-11. ( BEI Jianzhong, SUN Keli, LI Yuanyin, et al. Analysis of current force over a composite dike with tooth-shape structures by using CFX software[J]. Port Engineering Technology, 2017, 54(1): 7-11. (in Chinese)) |
| [5] |
闫杰超, 夏云峰, 张蔚, 等. 齿型构件混合堤正交丁坝水流力数值模拟[J]. 水运工程, 2017(4): 1-7. ( YAN Jiechao, XIA Yunfeng, ZHANG Wei, et al. The numerically simulation on drag force of the orthogonal spur dike with toothed mixture embankment[J]. Port and Waterway Engineering, 2017(4): 1-7. (in Chinese)) |
| [6] |
AZINFAR H, KELLS J A. Backwater effect due to a single spur dike[J]. Canadian Journal of Civil Engineering, 2007, 34(1): 107-115. DOI:10.1139/l06-117 |
| [7] |
AZINFAR H, KELLS J A. Backwater prediction due to the blockage caused by a single, submerged spur dike in an open channel[J]. Journal of Hydraulic Engineering, 2008, 134(8): 1153-1157. DOI:10.1061/(ASCE)0733-9429(2008)134:8(1153) |
| [8] |
OAK A G, SMITH C D. Backwater effect due to overtopping a spur dike[C]//Proceedings of the Annual Conference of the Canadian Society for Civil Engineering, Winnipeg, Man. Canadian Society for Civil Engineering (CSCE), Montréal, Que, 1994, 1: 136-145.
|
| [9] |
AZINFAR H. Flow resistance and associated backwater effect due to spur dikes in open channels[D]. Saskatoon: Saskatchewan, 2010.
|
| [10] |
AZINFAR H, KELLS J A. Drag force and associated backwater effect due to an open channel spur dike field[J]. Journal of Hydraulic Research, 2011, 49(2): 248-256. DOI:10.1080/00221686.2011.552470 |
| [11] |
YOSSEF M F M. Morphodynamics of rivers with Groynes[M]. Netherlands: Delft University, 2005.
|
| [12] |
BROEKHOVEN R W A V. Het effect van kribverlaging op de afvoercapaciteit van de Waal ten tijde van hoogwater[M]. Netherlands: TU Delft, 2007.
|
| [13] |
SHAW T L. Effect of side walls on flow past bluff bodies[J]. Journal of the American Veterinary Medical Association, 1971, 209(4): 767-771. |
2. Key Laboratory of Port, Waterway and Sedimentation Engineering of Ministry of Transport, Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2018
2018 