目前,我国长江、西江等黄金水道航道整治任务艰巨而繁重,逐步由以往的单滩或局部河段整治转向长河段的系统整治,因而迫切需要进行长河段泥沙模型试验,研究解决诸多工程中的关键技术问题。然而,对于长江中下游河段泥沙模型,因原型河道泥沙粒径很细,为满足泥沙运动相似要求,须采用轻质沙作为模型沙,由此产生了模型水流运动时间比尺和泥沙冲淤时间比尺不一致,即所谓的时间变态,从而影响到水流运动与泥沙冲淤的相似性,最终造成模型河床冲淤变形与原型河道不相似,甚至对长河段模型,使得试验无法进行,有可能成为最突出的相似性偏离问题。
关于泥沙模型时间变态问题,目前已有不少相关研究成果。近几十年来,欧美发达国家由于较少进行泥沙模型试验,因而大多数为我国学者的研究成果。例如,王兆印等[1]曾以流速形式表达连续方程,分析了时间变态影响的部分性质,所得一些试验资料与有关试验结果相同;吕秀贞等[2]定性和定量地分析了涨、落峰过程中模型沿程水位、流速及水流挟沙能力的偏离程度;张红武等[3]论述了黄河高含沙模型时间变态问题及解决途径的可能性;陈稚聪等[4]分析了时间变态与水流挟沙力关系;惠遇甲等[5]也分析了时间变态对模型相似影响,并提出相应的对策;邵学军等[6]通过模型试验和数值模拟计算,探讨了划分恒定流和非恒定流历时比例问题,并以三峡上引航道冲沙模型为实例,提出新方法;虞邦义等[7]利用淮河中游河段模型进行了相关研究,分析了时间变态引起的河段沿程水位、比降、流速和水流挟沙力等参数的偏离趋势;渠庚等[8-9]以长江防洪实体模型试验为例,采用一维数学模型计算的方法,分析了长河段河工模型时间变态对水流运动和河床冲淤变形的影响,并开展了不同时间变态率对洪水传播过程影响的试验研究,提出了改善时间变态效应的模型控制方法;张丽春[10]和高祥宇[11]则进行了时间变态问题理论上的深入研究。纵观上述研究,大多是时间变态对模型水流泥沙运动相似性的影响,所以目前对该问题的认识较为清晰,但关于时间变态校正方法及其效果的研究较少,仅有几个不成熟或不完善的措施或设想,并且相关研究多采用数学模型模拟物理模型试验为手段,无法反映模型水流延滞性和实际控制对试验结果的影响,特别是对长河段泥沙模型而言,这种影响往往成为关键的技术难点。因而,深入展开时间变态校正措施的研究,具有迫切的现实意义,同时在泥沙模拟理论和试验技术方面具有重要的学术价值。
1 时间变态成因及其影响根据河工模型相似理论,对于长江中下游河段泥沙模型,需满足以下水流和泥沙运动相似条件:
| $ 水流重力相似:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{V}}=\lambda _{H}^{1/2} $ | (1) |
| $ 水流阻力相似:\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{n}}=\lambda _{H}^{7/6}/{{\left( {{\lambda }_{V}}{{\lambda }_{L}} \right)}^{1/2}} $ | (2) |
| $ 水流运动时间相似:\ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{{{t}_{1}}}}={{\lambda }_{L}}/{{\lambda }_{V}} $ | (3) |
| $ 水流运动连续性相似:\ \ \ \ \ \ \ \ \ {{\lambda }_{Q}}={{\lambda }_{L}}{{\lambda }_{H}}{{\lambda }_{{{t}_{1}}}} $ | (4) |
| $ 泥沙起动相似:\ \ \ \ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{{{V}_{0}}}}={{\lambda }_{V}} $ | (5) |
| $ 泥沙沉降相似:\ \ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{\omega }}={{\lambda }_{V}}{{\lambda }_{H}}/{{\lambda }_{L}} $ | (6) |
| $泥沙悬浮相似:\ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{\omega }}={{\lambda }_{V}}~({{\lambda }_{H}}/\lambda _{L})^{\frac{1}{2}} $ | (7) |
| $ 输沙率相似:\ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{{{S}_{*}}}}={{\lambda }_{S}} $ | (8) |
| $ 河床变形时间相似:\ \ \ \ \ \ \ \ \ \ \ {{\lambda }_{{{t}_{2}}}}={{\lambda }_{{{\gamma }_{0}}}}{{\lambda }_{L}}/({{\lambda }_{V}}{{\lambda }_{S}}) $ | (9) |
由上述9个相似条件可知,推移质泥沙模型和悬移质泥沙模型均存在2个时间比尺,即水运动流时间比尺λt1和分别由推移质泥沙冲淤或悬移质泥沙冲淤产生的河床冲淤时间比尺λt2或λt3。所谓时间变态,是指水流运动时间比尺与河床冲淤时间比尺两者的不一致。定义M=λt2/λt1,M为河床变形时间比尺与水流运动时间比尺之比,即为时间变态率。
由式(9)有:
| $ M=\frac{{{\lambda }_{{{t}_{2}}}}}{{{\lambda }_{{{t}_{1}}}}}=\frac{{{\lambda }_{{{\gamma }_{0}}}}{{\lambda }_{L}}}{{{\lambda }_{S}}{{\lambda }_{V}}{{\lambda }_{{{t}_{1}}}}}=\frac{{{\lambda }_{{{\gamma }_{0}}}}}{{{\lambda }_{S}}} $ | (10) |
由上述相似条件,若不存在时间变态,两个时间比尺相等,即M=1,则有λγ0/λS=1,只有在正态模型中采用天然沙为模型沙时才能成立。但是,对于长江中下游此类平原细沙河流,受场地和试验设备等条件限制,一般采用变态模型,同时为满足起动和沉降、悬浮相似条件,并保证模型沙颗粒形态、休止角等特性与原型沙接近,不得不选用轻质沙,由此就会造成M>1。对于许多泥沙模型,河床冲淤时间比尺λt2为水运动流时间比尺λt1的数十倍甚至百倍。可见泥沙模型时间变态问题是客观存在的,主要是选用轻质沙和模型变态所引起,与模拟河段长度和其他因素无关。
泥沙模型试验操作中,水流强度由水流运动时间比尺控制,而水流作用时间则由河床变形时间比尺控制。通常是将天然河流非恒定的水沙过程概化为若干个恒定的梯级,各梯级中模型水流为恒定流,水流时间比尺失去意义。但在各梯级转换期间模型水流必然是非恒定流,尤其是在涨水和落水期间的梯级,如果存在时间变态,模型水流当地加速度项缩小为原来的1/M,使得实际水位、流速和流量过程线发生变形,可能会导致水流不相似,随着M的增大,不相似程度会增加,从而导致河床变形不相似。因而,时间变态的影响主要体现在一级流量转换过渡至另一级流量的非恒定流期间,关键是转换期的时间长短,或是在整个梯级概化的水沙过程中非恒定时间所占的比例。
关于泥沙模型时间变态对泥沙模型试验相似性的影响,已有不少相关研究,取得较清晰的认识,主要是:泥沙模型存在时间变态时,在概化梯级转换期间,涨峰过程使得模型沿程水位偏低,进口段流速偏大,中、下游段流速偏小;降峰过程则相反,模型沿程水位偏高,上游进口段流速偏小,中下游段流速偏大。从涨落峰全过程来看,在相应于天然洪峰时段内,时间变态影响的结果主要受涨峰过程控制,落峰过程还来不及反映,则往往又开始受接踵而来的下一个洪峰的影响。因而导致沿程流速、水位、挟沙能力和河床冲淤量的偏离,并直接影响到河床冲淤变形相似。对于长河段或是洪漫滩宽阔的河段,由于水流槽蓄作用较大,这种影响则会表现更明显,甚至前一个水文级尚未调整好,但已到了应调整下一个水文级的时间了,也即所谓的模型调整流量的时间不够,使得试验无法操作。因而,时间变态问题有可能成为长河段泥沙模型最突出的相似性偏离问题。
2 时间变态消减措施及存在问题如前述,选择轻质模型沙是泥沙模型时间变态最主要的原因,对于大多数平原细沙河流泥沙模型是无法回避的问题。处理时间变态问题最基本的方法就是将原型非恒定的水沙过程进行梯级概化,各梯级按恒定流水沙条件施放。虽然早期试验的原因可能是无法准确进行非恒定流控制,但更重要的是采用恒定梯级概化水沙过程,在客观上避免了时间变态的影响,可实现恒定梯级水沙过程下的模型河床变形与原型基本相似。但如此方法并未避免恒定梯级水沙过程转换期的模型水流、泥沙运动和河床冲淤变形的不相似性,甚至对于长河段模型因受时间变态影响而无法操作运行试验,因而,有必要进一步采取其他措施予以校正或消除或减弱这种影响。
关于消除或减弱泥沙模型时间变态措施的研究,至目前为数很少,根据我国近几十年泥沙模型试验的实践,所提出的相关措施大致有以下几种。
(1) 模型设计方面的考虑 依据黄河中游有关河段模型试验实践,张红武等[4]从模型比尺或模型沙选择出发,尽量使λt2≈λt1,从而避免时间变态的影响,实现水沙运动和河床冲淤变形的相似。此方法的基本点是认为引起时间变态的主要原因是利用不合适的含沙量比尺计算公式所致,因而根据黄河高含沙河流或枢纽库区淤积河段实际情况,模型设计时,选用合适的挟沙力公式计算原型输沙量,通过预备试验确定模型挟沙能力,如此得到λt2≈λt1。陈稚聪等[5]则针对长江枢纽淤积模型,建议选择重度较大的模型沙,尽量使原型沙的重度与模型沙的重度接近,即使λγ0接近1。这两种方法均存在一定的局限性。前一方法有其特定条件,所选用的挟沙力公式仅适用于高含沙河流,对于类似长江中下游平原细沙河流难以适用,因而无法设计得到λt2≈λt1;后一方法仅在理论上成立,但平原细沙河流一般河床质很细,如采用重质模型沙,就要求模型沙颗粒更细,不仅选沙困难,而且模型沙颗粒过细,即可能存在强黏性,造成起动不相似,引起更大的相似性偏离问题。
(2) 模型边界控制措施 从模型边界控制入手,或是通过调整恒定流和非恒定流的作用时间比例,或是改变模型进口流量控制和尾门水位控制,保证主要水动力的时间(即恒定梯级时间),使模型水流造床作用尽量与原型接近。前一方法由邵学军等[7]通过三峡水库上游引航道模型(正态模型1:180)试验总结提出,此方法方向正确,但对于长江中下平原细沙河流,往往是涨落水的非恒定流期间河床冲淤变化大,如何划分和调整恒定流和非恒定流的作用时间比例,需要大量的探索和试验作依据。后一方法是惠遇甲等[6]通过长江葛洲坝枢纽回水变动区泥沙模型试验中总结提出,控制模型进口流量和尾门水位,适当改变流量变换期间的水流过程,即涨水阶段适当加大进口流量、加速提高尾门水位;落水阶段适当减少进口流量、加速消落尾门水位,使模型水流过程在短时间(5~10 min)内达到控制值。这些措施能够在一定程度上纠正时间变态的影响,在时间和空间上都有助于达到泥沙冲淤过程相似的要求,但未根本解决问题,模型进口与尾门调节作用是有限的,且这些校正措施本身可能会引起新的偏差,尤其是对于长河段模型及2个时间比尺相差过多的模型,因而合理性和适用性受到质疑。
(3) 沿程实行补水或排水措施 从缩短概化梯级时间(即非恒定流时间)的角度出发,在模型沿程实行补(排)水的措施,即在流量变换(非恒定流)期间,模型沿程进行均匀补水或排水,在不破坏模型地形的前提下,使模型水流过程在短时间(5~10 min)内达到控制值。此办法首先由王兆印等[7]提出,也得到许多认同,应具有较好的合理性和可行性,但由于该项措施供排水设备量大且控制复杂,仅停留在设想层面,目前尚无实例。
(4) 调整模型水沙过程概化方式 由于模型水沙过程的恒定梯级概化并没有统一或固定的方式,基本上是根据试验人员的经验初定,再通过河床变形验证试验来确定,因而可采用恒定流与非恒定流相结合的方式进行模型水沙过程的梯级概化,只要使主要水沙过程时间尽量与原型接近,就可保证模型相似性。鉴于此,模型试验总时间和恒定流期间按河床变形时间比尺λt2控制,流量稳定期采用长时段梯级概化方式控制,涨落水期间采用短时段(甚至逐日)梯级概化方式控制。此办法虽然在理论上有一定的缺陷,但只要试验结果偏差在允许范围内,仍属于较为切实可行的方法,但目前还尚无实例,需要大量试验成果予以支撑。
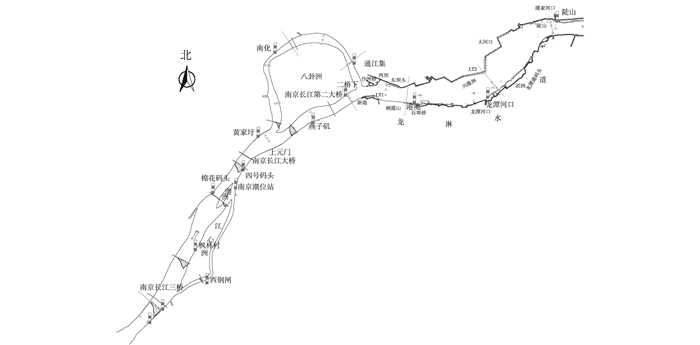
3 实例及消减措施探讨本文以长江南京河段模型为实例,基于前文消减时间变态影响第4种措施的思路,进行水沙过程概化方式调整及模型相似性的探索研究。如图 1,南京河段模型范围上起长江三桥以上约3 km,下迄龙潭水道上段的九乡河,全长约43 km,包括梅子洲左、右汊,潜洲左、右汊以及八卦洲左、右汊。南京河段多年平均流量为28 300 m3/s,三峡水库蓄水后2003—2009年多年平均含沙量为0.18 kg/m3,多年平均输沙量为1.48亿t;年内汛期5—10月径流占全年的70%以上,悬移质含沙量的变化与径流的年内变化基本同步;河床质为中细沙,中值粒径0.15 mm,悬沙床沙质起主要造床作用,中值粒径为0.09 mm。
|
图 1 长江南京河段模型范围 Figure 1 Scope of Nanjing reach model of the Yangtze River |
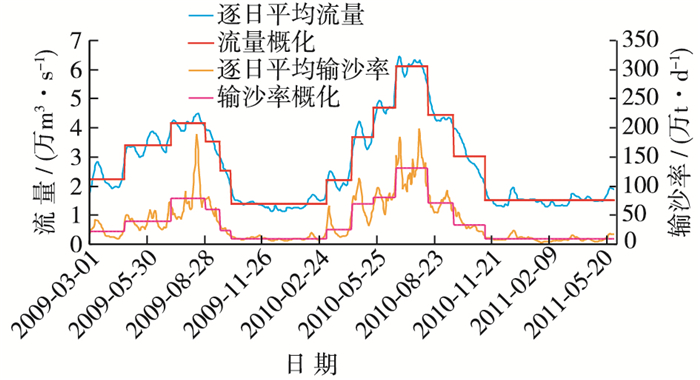
模型平面比尺为1:480,垂直比尺为1:120;选用防腐木屑为模型沙,颗粒密度为1 140 kg/m3;干密度为400 kg/m3,最终确定的模型水流和泥沙比尺见表 1。依据2009年3月至2011年6月实测水沙和河床地形资料,按常规方法对水沙过程进行恒定梯级概化(见图 2),试验验证表明模型水流运动及河床冲淤变形与原型基本一致,相似性较好。
| 表 1 模型水流和泥沙比尺 Table 1 Flow and sediment scales of the model |
|
图 2 模型水沙过程恒定梯级概化 Figure 2 Generalized constant step of water and sediment process of the model |
依据消减时间变态影响第4种措施的思路,同样针对2009年3月至2011年6月水沙过程,模型试验总时间仍按河床冲淤时间比尺λt2确定,但期间水沙过程则按逐日平均进行概化,即将模型水沙过程的概化梯级时段长度设为1 d,也就是模型进口流量、加沙量和尾门水位均按图 2中的逐日平均值进行自动控制,模型进口流量大小基本由水流运动时间比尺控制确定,并根据实际情况及时予以调整。通过观测试验过程中模型各处水流特征和试验结束后最终地形,检验其与验证试验(即水沙过程恒定梯级概化试验)结果的区别,以及与原型河道实测数据的差异。分析2种水沙过程概化方式的试验结果,可得到以下几点认识:
(1) 按逐日平均概化水沙过程,模型中水流属于非恒定流,上、中、下各处水位和深泓垂线平均流速随时变化,但与常规的恒定梯级概化试验结果相比,沿程水位和流速处于同一个量级之中,模型水流总量及涨、落水期的水量基本接近,同时,模型上、中、下各段河床断面冲淤变形相差也不大,冲淤量变化在5%以内,处于模型控制允许的误差范围。这表明按2种水沙过程概化方式进行模型试验,河道水流、泥沙运动特征和河床冲淤变化总体特征基本相同。
(2) 按2种水沙过程概化方式进行试验,模型水流和河床冲淤变化均与天然原型基本相似,符合水利和水运行业模型试验规程的相似性要求。
(3) 按水沙过程恒定梯级概化方式进行试验,在涨落水期的流量转换期,如过渡段时间小于5 min,水流将出现突变现象,说明时间变态影响较为明显,对于水沙过程过于尖瘦的情况,若恒定概化梯级时间过短则反而失真严重;按水沙过程逐日平均概化进行试验,由于模型水流随时调整,上、中、下各处基本上未出现重大突变现象,基本可规避时间变态这一问题。
(4) 2种方式的试验结果对比表明,按逐日平均概化方式进行泥沙试验基本可行,因而有望在长河段模型试验中解决或消除时间变态所带来的涨水水量不足和落水水量难消的难题。但是,水沙过程按逐日平均概化进行泥沙模型试验,涉及到模型非恒定流输沙问题,在相似性理论方面尚存在值得探讨的问题,此方式究竟在多长河段模型中适用,或是其削弱时间变态影响的量化程度,以及其中模型各项水流、泥沙各项比尺的变化过程等等问题,亦有待更多的实践予以检验。
4 结语本文针对泥沙模型时间变态影响及其消减措施的问题,采用理论分析和实例试验相结合的方法,进行了较为全面和深入的探讨,主要得到以下几点结论:
(1) 泥沙模型时间变态问题是客观存在的,主要是选用轻质沙和模型变态所引起,与模拟河段长度和其他因素无关。关于时间变态对模型水流泥沙运动相似性的影响,目前认识较为清楚,但对于消减措施研究不足,存在较多问题,尤其对长河段泥沙模型,甚为突出。
(2) 关于消除或减弱泥沙模型时间变态影响的措施或设想,主要有模型设计方面的考虑、模型边界控制措施、沿程实行补水或排水措施、调整模型水沙过程概化方式的措施等,虽各自有一定依据,但均存在不足或缺陷。
(3) 长江南京河段泥沙模型试验结果表明,按水沙过程逐日平均概化方式进行动床泥沙试验,与常规的恒定梯级概化试验相比,水流、泥沙运动和河床冲淤变化特征和规律基本接近,且与天然原型基本相似。因此,说明这种试验方法基本可行,有望在长河段模型试验中解决或消除时间变态所带来的涨水水量不足和落水水量难消的难题,但在相似性理论方面尚存在值得探讨的问题,还有待更多的实践予以检验。
| [1] |
王兆印, 黄金池. 泥沙模型试验中的时间变态问题及其影响[J]. 水利学报, 1987(10): 48-53. ( WANG Zhaoyin, HUANG Jinchi. Time deformation problem in sediment model test and its influence[J]. Journal of Hydraulic Engineering, 1987(10): 48-53. DOI:10.3321/j.issn:0559-9350.1987.10.006 (in Chinese)) |
| [2] |
吕秀贞, 戴清. 泥沙河工模型时间变态的影响及其误差校正途径[J]. 泥沙研究, 1989(2): 12-24. ( LYU Xiuzhen, DAI Qing. A study on time scale distortion of sediment physical model and the measures to correct its dissimilarity[J]. Journal of Sediment Research, 1989(2): 12-24. (in Chinese)) |
| [3] |
张红武, 江恩惠. 黄河高含沙洪水模型的相似律[M]. 郑州: 河南科学技术出版社, 1994. ( ZHANG Hongwu, JIANG Enhui. Similarity law on flood model of high sediment concentration in the Yellow River[M]. Zhenzhou: Henan Science and Technology Press, 1994. (in Chinese))
|
| [4] |
陈稚聪, 安毓琪. 河工模型中时间变态与水流挟沙力关系的试验研究[J]. 人民长江, 1995, 26(8): 51-54, 63. ( CHEN Zhicong, AN Yuqi. Experimental study on relation between time scale distortion in river model test and sediment-carrying capacity[J]. Yangtze River, 1995, 26(8): 51-54, 63. (in Chinese)) |
| [5] |
惠遇甲, 王桂仙. 河工模型试验[M]. 北京: 中国水利水电出版社, 1999. ( HUI Yujia, WANG Guixian. River engineering model test[M]. Beijing: China Water and Power Press, 1999. (in Chinese))
|
| [6] |
邵学军, 王睿禹, 李俊凯. 非恒定流冲沙模型时间比尺变态及其修正方法[J]. 水力发电学报, 2007, 26(6): 96-100, 82. ( SHAO Xuejun, WANG Ruiyu, LI Junkai. Time scale distortion in a movable-bed unsteady flow test and its improvement methods[J]. Journal of Hydroelectric Engineering, 2007, 26(6): 96-100, 82. (in Chinese)) |
| [7] |
虞邦义, 吕列民, 俞国青. 河工模型时间变态问题试验研究[J]. 泥沙研究, 2006(2): 22-28. ( YU Bangyi, LYU Liemin, YU Guoqing. Experiment investigation on time scale distortion in river model tests[J]. Journal of Sediment Research, 2006(2): 22-28. (in Chinese)) |
| [8] |
渠庚, 郭熙灵, 龙超平, 等. 泥沙实体模型时间变态问题的研究[J]. 水利学报, 2007, 38(11): 1318-1323. ( QU Geng, GUO Xiling, LONG Chaoping, et al. Study on time scale distortion problem in sediment model test[J]. Journal of Hydraulic Engineering, 2007, 38(11): 1318-1323. DOI:10.3321/j.issn:0559-9350.2007.11.008 (in Chinese)) |
| [9] |
李发政, 孙贵洲, 渠庚. 长河段河工模型时间变态影响及水沙过程控制方式研究[J]. 长江科学院院报, 2011, 28(3): 75-80. ( LI Fazheng, SUN Guizhou, QU Geng. Research on influence of time scale distortion and control model of water-sediment process in long river reach physical model[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(3): 75-80. (in Chinese)) |
| [10] |
张丽春. 泥沙物理模型试验时间变态问题的研究[D]. 北京: 清华大学, 2000. (ZHANG Lichun. Study on the problem of time distortion in physical modeling of sediment transport[D]. Beijing: Tsinghua University, 2000. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=Y360043
|
| [11] |
高祥宇. 泥沙物理模型时间变态影响研究[D]. 南京: 南京水利科学研究院, 2014. (GAO Xiangyu. Study on influence of time distortion in physical modeling[D]. Nanjing: Nanjing Hydraulic Research Institute, 2014. (in Chinese))
|
 2018
2018 