大坝变形最能直观可靠地反映其服役性态,对大坝变形原型观测资料进行分析处理并建立实时预报模型是大坝安全监控领域中的前沿性研究内容[1-2]。限于当前监测技术及分析理论制约,常规统计模型中主要考虑水压、温度及时效的影响[3],而对其结构损伤、流固耦合、节理裂隙及量测等不确定信息影响的考虑欠佳,在拟合精度与预报能力上难以进一步提高。因此,如何根据大坝原型观测资料建立较为精确的大坝变形预报模型,对及时掌握大坝服役性态和确保大坝长期安全运行具有重要意义[4-5]。
当前,基于大坝变形观测资料建立预报模型的方法较多,模糊数学[6]、BP神经网络[7]、时间序列[8]、灰色理论[9]、D-S证据理论[10]、人工蜂群算法[11]、遗传算法[12]、混沌理论[13-14]、系统优化模型[15]等方法在大坝变形分析预报中得到了广泛应用。但上述方法多针对大坝变形及其主要影响因素信息的挖掘,在大坝变形与其影响因子之间的复杂非线性关系及不确定信息因素影响等方面考虑欠佳[16]。同时,实际工程监测中,监测数据难免受到环境等因素影响而存在噪声,进一步限制了模型预报精度的提升。伴随计算机技术与监测信息处理技术的发展,支持向量机[17-19]、谱分析[20]等方法有效应用于原型监测数据中有效成分的提取,但多针对较为平稳的系统信号,对于看似随机但却表现出确定非线性的随机信号考虑不足。
考虑到大坝变形观测数据的演化与内外环境影响因素之间蕴含的依存关系亟待挖掘,采用多尺度小波分析技术对变形观测数据进行分解,分解后所得系统信号频率较低,具有较为明显的趋势性与规律性,该信号内蕴了水压、温度等周期性因子的影响;随机信号频率较高、非线性特征明显,包含了时效等不确定信息与噪声因素的影响。基于上述特征,分别利用ARIMA模型与BP神经网络对变形观测数据内蕴含的系统信号与随机信号分项训练预报,并将两者预报值相叠加,得到了基于BP-ARIMA的混凝土坝多尺度变形组合预报值。以某碾压混凝土坝为研究对象,分析所建组合模型的预报精度,以验证该模型的科学性与有效性。
1 大坝变形观测数据的多尺度小波预处理小波分析[21]是一种时频分析方法,主要思想是认为监测信号中不同频率分量具有不同时变特性,高频分量具有随时间变化迅速的频谱特征,低频分量具有随时间变化缓慢的频谱特征,据此规律非均匀划分时间轴和频率轴,可在不同时频区得到较合理的时间和频率分辨率,具有良好的多分辨率分析特点[22-23]。小波技术可根据系统信号和随机信号的频率特征实现二者分离,将时域信息与频域信息有机结合,在提取信号频率特征的同时保持了时域特征[24]。
受水位、温度与时效等因子及仪器量测精度不确定性等因素的影响,大坝变形观测数据常包含系统信号与随机信号,两种信号具有明显不同的频率特征,系统信号频率较低,具有较为明显的趋势性与规律性,常认为是水压、温度等周期性影响因子作用的结果;随机信号频率较高,非线性特征明显,大坝服役期间坝体及坝基材料参数演变、坝体内部结构损伤、节理裂隙、流固耦合以及仪器量测误差等不确定性因素是导致其离散性较高的主要原因。设大坝变形观测资料S(H, T, θ)满足S(H, T, θ)∈L2(R),以3层分解为例对S(H, T, θ)进行小波分解,其分解过程如图 1所示。
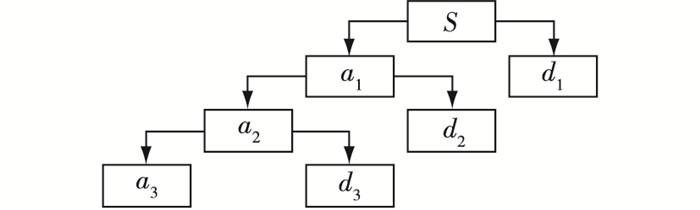
|
图 1 小波分解示意 Figure 1 Schematic diagram of wavelet decomposition |
由图 1可知,S(H, T, θ)经小波逐层分解后得到了低频信号a3和高频信号d1,d2,d3,故原型观测信号在分解尺度J下的分解表达式为:
| $ S\left( {H, T, \theta } \right) = A_{_J}^{^d}f + \sum\limits_{j \le J} {{D_j}} f $ | (1) |
式中:AJdf为轮廓信号,即系统信号;
| $ A_{_J}^{^d}f = \sum\limits_{k \in Z} {\left\langle {S\left( {H, T, \theta } \right), {\varphi _{J, k(x)}}} \right\rangle } {\varphi _{J, k}}\left( x \right) = \sum\limits_{k \in Z} {{c_{J, k}}{\varphi _{J, k}}\left( x \right)} $ | (2) |
| $ {D_j}f = \sum\limits_{k \in Z} {\left\langle {S\left( {H, T, \theta } \right), {\mathit{\Psi }_{J, k(x)}}} \right\rangle } {\mathit{\Psi }_{J, k}}\left( x \right) = \sum\limits_{k \in Z} {{d_{J, k}}} {\mathit{\Psi }_{J, k}}\left( x \right) $ | (3) |
式中:φJ, k(x)为尺度函数;cJ, k为尺度展开系数;ψJ, k(x)为小波函数;dJ, k为小波展开数;k为分解层数;Z为整数集。
2 BP-ARIMA变形组合预报模型的构建 2.1 随机信号的BP神经网络预报BP神经网络是指采用误差反向传播算法(Back Propagation,BP)的多层前馈型神经网络,具有较强的计算能力,可以表达多种复杂的映射。随机信号具有较强的非线性特征,是某种依赖关系的直接体现,视为非平稳序列,组合各阶高频信号序列利用BP神经网络进行拟合预报。本文采用3层BP神经网络结构,网络学习的过程具体如下:
(1) 对于给定神经元xj,网络的输入与输出分别为
| $ {y_j} = {W_{ji}}{x_j} + {\theta _j} $ | (4) |
| $ {Z_j} = \frac{1}{{1 + {\rm{exp}}(-\sum {W_{ji}}{x_j}-{\theta _j})}} $ | (5) |
式中:W为二者之间的权重;θ为阈值。
(2) 计算各层节点误差信号
| $ {\gamma _j} = (Z{^\circ _j}- {Z_j})\frac{{{\rm{exp}}(- \sum {W_{ji}}{x_j}- {\theta _j})}}{{{{[1 + {\rm{exp}}(-\sum {W_{ji}}{x_j}-{\theta _j})]}^2}}} $ | (6) |
式中:Z°j为神经元的期望输出。
(3) 权值修正
| $ W_{_{ji}}^{^{{\rm{new}}}} = W_{_{ji}}^{^{{\rm{old}}}} + \alpha {\gamma _j}{Z_j} $ | (7) |
式中:α为学习率。
(4) 网络收敛判别
| $ E = \frac{1}{2}\sum\limits_{i = 1}^n {[{{({Z_j}-Z{^\circ _j})}^2}]} $ | (8) |
式中:Zj和Zj°分别表示实际输出与期望输出;n为样本总数。当神经网络自学习获得的网络收敛判别依据E小于给定拟合误差时,结束网络训练。
2.2 系统信号的ARIMA模型预报ARIMA模型是将ARMA(p, q)模型与差分运算有机结合起来,具有精度较高的短期预测功能,是描述非平稳时间序列的重要方法[25],也常写作ARIMA(p, d, q)模型。建模的基本思想是使用差分法对非平稳时间序列进行平稳化处理,通过观察相关函数截尾和拖尾特征、自回归阶数(p)、差分次数(d)和移动平均阶数(q)3个参数,进而对时间序列进行预测分析。系统信号较为平滑,为近似平稳的时间序列,该组随机变量一方面表现出预报数据在时间上的延伸,另一方面受环境扰动亦表现出自身的变动规律。ARIMA模型结构如下:
| $ \left\{ \begin{array}{l} (1-{\phi _1}B-{\phi _2}{B^2}-\cdots - {\phi _p}{B^p}){\nabla ^d}{x_t} = (1 - {\theta _1}B - {\theta _2}{B^2} - \cdots - {\theta _q}{B^q}){\delta _t}\\ E({\delta _t}) = 0, Var({\delta _t}) = \sigma _{_\varepsilon }^{^2}, E({\delta _s}{\delta _t}) = 0, s \ne t \end{array} \right. $ | (9) |
式中:xt(t=0, 1, 2, …, n)为系统信号,xt与xt-i(i=1, 2, …, p)相关,δt为ARIMA模型误差,δt与δt-j(j=1, 2, …, q)相关;B为延迟算子且满足Bnxt=xt-n;d为差分算子,dd=(1-B)d;ϕ1, ϕ2, …, ϕp为自回归系数,θ1, θ2, …, θq为滑动平均系数。δt满足:
| $ {\delta _t} = {\theta _1}{\delta _{t-1}} + {\theta _2}{\delta _{t-2}} + \cdots + {\theta _q}{\delta _{t-q}} - {\phi _t} - {\phi _1}{x_{t - 1}} - {\phi _2}{x_{t - 2}} - \cdots - {\theta _p}{x_{t - p}} - {x_t} $ | (10) |
满足式(9)的模型即为ARIMA(p, d, q)模型。ARIMA预报模型的建立主要通过以下4个步骤实现:
(1) 平稳性检验与平稳化处理。采用时间序列的散点图、自相关函数(ACF)、偏自相关函数图(PACF)和单位根ADF检验时间序列的平稳性,若数据序列非平稳,并存在一定的增长或下降趋势,则需对数据进行d阶差分处理,即序列平稳化处理。
(2) 模型识别与定阶。平稳性检验或d阶差分平稳化处理后,根据自相关函数ACF和偏自相关函数PACF分析确定适合该序列的ARIMA(p, d, q)模型形式,即判断模型形式为AR(p), MA(q)或ARMA(p, q)模型。在确定模型形式后,一般采用AIC标准定阶对其阶数进行定阶,AIC标准的定阶方法为
| $ AIC\left( {p, q} \right) = \mathop {{\rm{min}}}\limits_{0 \le m, n \le L} AIC\left( {m, n} \right) = {\rm{min}}\left\{ {N{\rm{ln}}{{{\rm{ \mathsf{\hat σ} }}}^2} + 2\left( {m + n + 1} \right)} \right\} $ | (11) |
式中:L为预先给定的模型阶数上限;
(3) 参数估计。模型参数包括ϕ1, ϕ2, …, ϕp和θ1, θ2, …, θq及
据计算残差
| $ {x_t} = \sum\limits_k^p {{\phi _k}{x_{t-k}}} + {{\hat \delta }_t} + \sum\limits_k^q {{\theta _k}} {{\hat \delta }_{t-k}} $ | (12) |
式中:k=p+1,p+2, …, N;t=L+1, L+2, …, N;
目标函数
| $ Q\left( {\phi, \theta } \right) = {({\delta _t}-\sum\limits_k^p {{\phi _k}} {\delta _{t-k}}-\sum\limits_k^q {{\theta _k}} {{\hat \varepsilon }_{t - k}})^2} $ | (13) |
对式(13)极小化可得
| $ {{\hat \sigma }_2} = \frac{1}{{N-L}}Q({{\hat \phi }_1}, {{\hat \phi }_2}, \cdots, {{\hat \phi }_p}, {{\hat \theta }_1}, {{\hat \theta }_2}, \cdots, {{\hat \theta }_q}) $ | (14) |
φ,θ的最小二乘估计计算方法定义为:
| $ \begin{array}{l} x = \left[{\begin{array}{*{20}{c}} {{x_{L + 1}}}\\ {{x_{L + 2}}}\\ \vdots \\ {{x_N}} \end{array}} \right], \hat x = \left[{\begin{array}{*{20}{c}} {{x_L}}&{{x_{L-1}}}& \cdots &{{x_{L-P + 1}}}\\ {{x_{L + 1}}}&{{x_L}}& \cdots &{{x_{L-P + 2}}}\\ \vdots&\vdots &{}& \vdots \\ {{x_{N - 1}}}&{{x_{N - 2}}}& \cdots &{{x_{N - P}}} \end{array}} \right], \\ \hat \delta = \left[{\begin{array}{*{20}{c}} {{{\hat \delta }_L}}&{{{\hat \delta }_{L-1}}}& \cdots &{{{\hat \delta }_{L-P + 1}}}\\ {{{\hat \delta }_{L + 1}}}&{{{\hat \delta }_L}}& \cdots &{{{\hat \delta }_{L-P + 1}}}\\ \vdots&\vdots &{}& \vdots \\ {{{\hat \delta }_{N - 1}}}&{{{\hat \delta }_{N - 2}}}& \cdots &{{{\hat \delta }_{N - P}}} \end{array}} \right], \beta = \left[\begin{array}{l} \phi \\ \theta \end{array} \right] \end{array} $ | (15) |
目标函数(13)则可写作
| $ Q\left( {\phi, \theta } \right) = \left| {x-\hat x\varphi-\hat \delta \theta } \right| = {\left| {x-\left( {\hat x, \hat \delta } \right)\beta } \right|^2} $ | (16) |
故,根据
| $ \left[\begin{array}{l} \phi \\ \theta \end{array} \right] = \left[{\begin{array}{*{20}{c}} {{{\hat x}^{\rm{T}}}\hat x}&{{{\hat x}^{\rm{T}}}\hat \delta }\\ {\hat \delta \hat x}&{{{\hat \delta }^{\rm{T}}}\hat \delta } \end{array}} \right]\left[{\begin{array}{*{20}{c}} {{{\hat x}^{\rm{T}}}\hat x}\\ {{{\hat \delta }^{\rm{T}}}\hat x} \end{array}} \right] $ | (17) |
(4) 诊断与检验。模型诊断与检验的目的是根据拟合时段的残差,分析模型精度以检验其适用性。自相关函数法对模型进行统计检验的基本思想是训练值与ARIMA模型估计值的残差序列
| $ {Q_M} = N\sum\limits_{k = 1}^M {\rho _{_\varepsilon }^{^2}\left( k \right)} $ | (18) |
式中:N为样本容量;ρε2(k)为样本自相关系数,M取N/10[26]。对于给定的显著性水平α, 查表得Xα2(M)<QM,则在显著性水平α上否定假设H0,重新选择较为合适的模型;反之,认为模型拟合良好,经过上述步骤获得较优的预测模型后,即可用于残差序列系统信号的预报。
2.3 BP-ARIMA混凝土坝变形组合预报模型的构建结合上述理论,将大坝变形实测资料利用多尺度小波分解后所得的随机信号与系统信号分别结合BP神经网络与ARIMA模型进行训练和预报,并按照相应日期将其预报值进行叠加,至此得到了基于BP-ARIMA模型的混凝土坝变形组合预报值。本文提出基于多尺度小波分解与重构的BP-ARIMA混凝土坝变形组合预报模型构建流程如图 2所示。
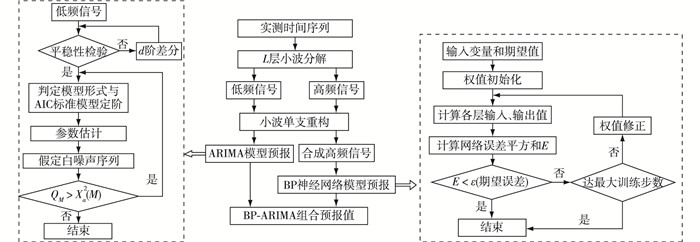
|
图 2 模型构建流程 Figure 2 Flowchart of model formation |
某混凝土重力坝最大坝高113.0 m,坝顶高程179.0 m,正常蓄水位与校核洪水位高程分别为173.0和177.8 m,调节库容与总库容分别为11.22亿m3和20.35亿m3。该坝布置了包括变形、渗流、温度以及应力应变等较为全面的监测项目,用以监测大坝变位的项目主要有正、倒垂线、引张线和视准线等,其中水平顺河向、垂直水流向位移量利用正、倒垂线监测,布置方案见图 3。
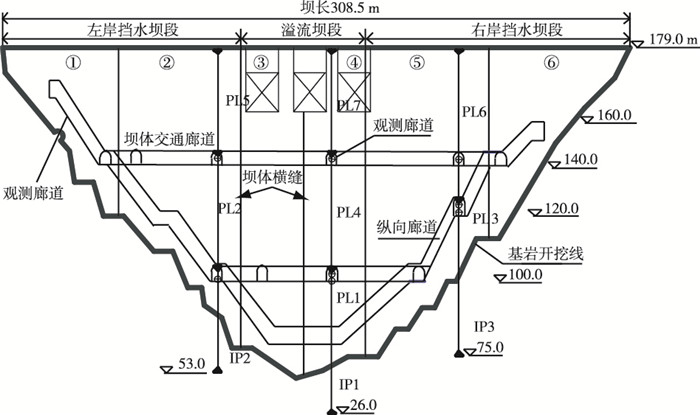
|
图 3 大坝变形监测布置方案 Figure 3 Arrangement of measuring points |
选取2#坝段2006年6月1日至2008年5月31日正垂线测点PL2(140 m)水平位移自动化监测序列进行分析,剔除异常干扰值,并经等时间间隔处理后,得到一个包含689组数据的位移实测序列,以前670组监测数据作为模型训练样本,后19组数据进行预报。监测时段内上游水位过程线与测点实测位移过程线如图 4所示。
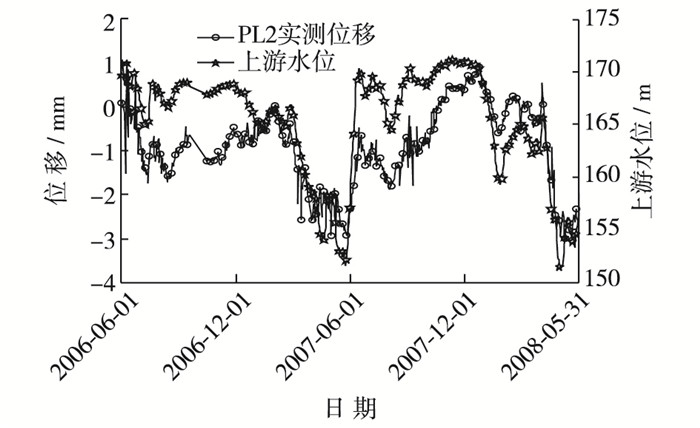
|
图 4 PL2测点位移实测过程线与上游水位过程线 Figure 4 Hydrograph of upstream water level and measured deformation of PL2 |
由图 4可知,测点PL2位移实测序列与水深序列变化趋势完全一致,当上游水深减小时,坝体向上游的位移增大;反之,坝体向下游的位移增大。为尽量减少实测信号的损失,根据工程经验,选取MATLAB小波分析工具箱中dbN小波系的db4小波对测点位移实测信号进行3层分解,获得1组系统信号序列a3,3组随机信号序列d1,d2,d3,分解所得的系统信号与随机信号序列长度与水平位移自动化监测序列长度相等,其分解结果见图 5。

|
图 5 PL2测点小波3层分解 Figure 5 Decomposition results of residual sequence of PL2 |
由图 5可知,系统信号序列a3平滑度较好,变化趋势与大坝变形观测数据一致,随机信号序列d1,d2,d3较离散,但表现出一定的周期性,初步分析应是受水位、温度等周期性因素影响。为便于对各频段信号分别建模计算,将上述分解所得随机信号序列按相应日期叠加进行重构,合成结果如图 6所示。
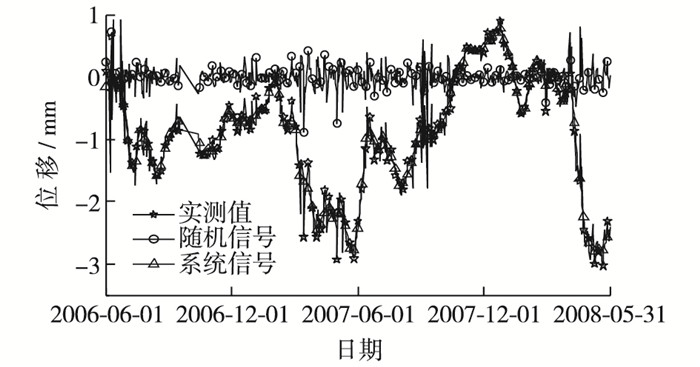
|
图 6 PL2测点信号合成曲线 Figure 6 Reconstruction result of residual sequence of PL2 |
由图 6可知,随机信号表现出明显的离散性,为非稳定性数据,采用BP神经网络建模分析;系统信号较位移实测序列更平滑、稳定性更好,采用ARIMA方法建模分析。将2种方法所得的拟合预报值叠加即为组合预报值。其中,ARIMA模型的参数为p=0,d=2,q=7;BP神经网络采用由表示条件属性输入的输入层、决策属性输出的输出层和隐藏层3层结构实现,输入层对应坝体位移的主要影响因子,如水压、温度与时效,有9个节点;输出层对应相应坝体位移,有1个节点;隐含层节点数取11。BP神经网络收敛曲线如图 7所示,其参数设置为:网络最大训练次数为2 000;训练的最大允许误差为0.005;网络学习速率为0.01。
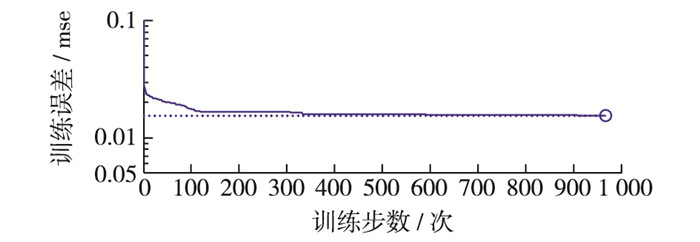
|
图 7 网络训练过程收敛曲线 Figure 7 Network training process convergence curve |
为了验证组合模型预报结果的有效性,同时建立了PL2测点的回归模型与BP模型,3种方法拟合及预报结果如图 8所示,残差序列对比见图 9。
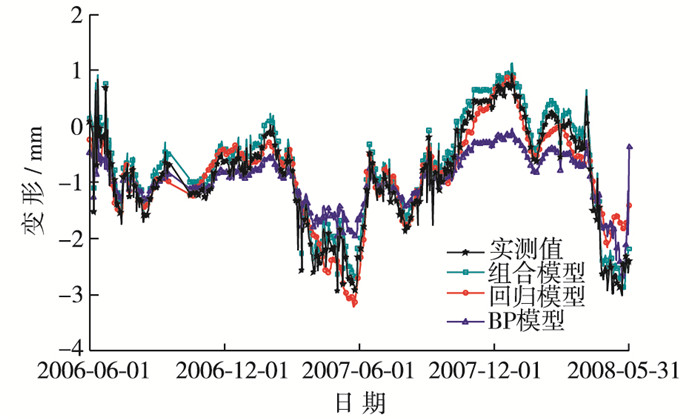
|
图 8 PL2测点变形拟合及预报结果 Figure 8 Displacement fitting and forecast results of PL2 |

|
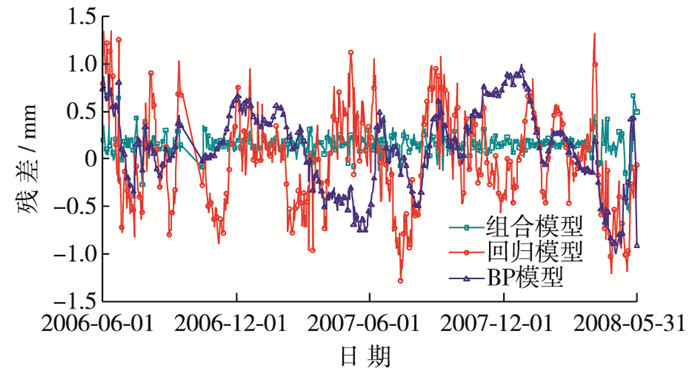
图 9 PL2测点残差序列对比 Figure 9 Contrast diagram of residual sequences of PL2 |
为进一步验证所建模型的预报结果,运用本文方法,以PL5(179.0 m)测点为参照点预报其相应时段的大坝变位,并将其拟合与预报结果及残差序列分别绘制于图 10和11。同时,对3种模型的预报精度进行深入比较,分别量化计算了PL2与PL5测点的模型预报结果统计指标,如平均误差(mean error, ME)、均方误差(mean square error, MSE)和平均绝对百分误差(mean absolute percentage error, MAPE),如表 1所示。
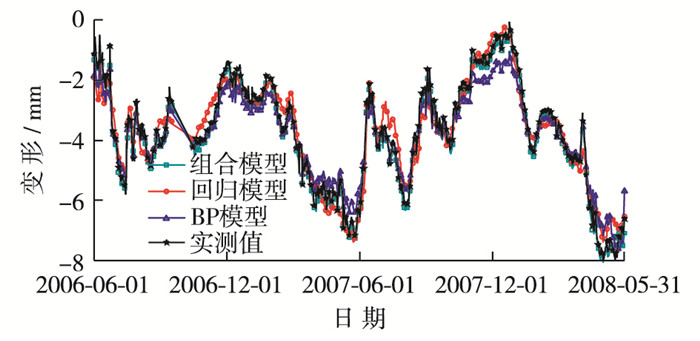
|
图 10 PL5测点变形拟合及预报结果 Figure 10 Displacement fitting and forecast results of PL5 |
|
图 11 PL5测点残差序列对比 Figure 11 Contrast of residual sequences of PL5 |
| 表 1 3种预报模型的统计指标比较 Table 1 Statistical indexes of three forecast models |
通过PL2与PL5测点的实例分析,由图 8~11可见3种模型的拟合值、预报值与实测值变化规律一致,表明本文所建模型的有效性。同时,较回归模型、BP模型相比,组合预报模型的拟合值和预报值更贴近变形实测值,且其拟合与预报误差更小,说明该模型较常规监测模型的预报精度更优,由此验证了所建立的组合预报模型的合理性和科学性。表 1中的统计指标进一步佐证了组合模型相较回归模型与BP模型,有效地减小了预报误差,提高了预报精度。究其原因主要有以下两点,首先,本文所建组合预报模型充分捕捉了大坝变形观测资料中所蕴含的有效成分,有效克服了常规模型信息挖掘手法单一的缺陷;其次,采用小波分析技术对其进行分解与重构,并采用BP神经网络与ARIMA对所分解信号分频训练,充分挖掘了监测资料中所蕴含的时变特性与混沌特性。
4 结语(1) 本文结合小波分析技术、BP神经网络理论与ARIMA模型建立了基于BP-ARIMA的混凝土坝多尺度变形组合预报模型,较常规模型而言,该模型可以捕捉到变形监测信号中绝大部分数据特征,有效弥补了常规模型信息挖掘手法单一的缺陷。
(2) 采用ARIMA模型和BP神经网络对不同特征信号的训练优势分项建立预报模型,充分提取了监测信息中所蕴含时变特性与混沌特性。工程实例表明,文中所建模型的拟合与预报精度较常规模型有明显提高,从而佐证了所建模型的有效性。
(3) 本文所建方法计算简便高效,亦为高边坡及水工建筑物中等其他监控指标的拟定与预报提供了新方法,在实际工程领域中具有一定的推广应用价值。
| [1] |
丛培江, 顾冲时, 谷艳昌. 大坝安全监控指标拟定的最大熵法[J]. 武汉大学学报(信息科学版), 2008, 33(11): 1126-1129. ( CONG Peijiang, GU Chongshi, GU Yanchang. Maximum entropy method for determining dam safety monitoring indices[J]. Geomatics and Information Science of Wuhan University, 2008, 33(11): 1126-1129. (in Chinese)) |
| [2] |
曹茂森, 邱秀梅, 夏宁. 大坝安全诊断的混沌优化神经网络模型[J]. 岩土力学, 2006, 27(8): 1344-1348. ( CAO Maosen, QIU Xiumei, XIA Ning. A chaos-optimized neural network model for dam safety monitoring[J]. Rock and Soil Mechanics, 2006, 27(8): 1344-1348. (in Chinese)) |
| [3] |
吴中如. 水工建筑物安全监控理论及其应用[M]. 北京: 高等教育出版社, 2003. ( WU Zhongru. Safety monitoring theory and its application of hydraulic structures[M]. Beijing: Higher Education Press, 2003. (in Chinese))
|
| [4] |
徐伟, 何金平. 基于多尺度小波分析的大坝变形自回归预测模型[J]. 武汉大学学报(工学版), 2012, 45(3): 285-289. ( XU Wei, HE Jinping. Forecast model of dam deformation based on multi-scale wavelet analysis and autoregressive method[J]. Engineering Journal of Wuhan University, 2012, 45(3): 285-289. (in Chinese)) |
| [5] |
张豪, 许四法. 基于经验模态分解和遗传支持向量机的多尺度大坝变形预测[J]. 岩石力学与工程学报, 2011, 30(增刊2): 3681-3688. ( ZHANG Hao, XU Sifa. Multi-scale dam deformation prediction based on empirical mode decomposition and genetic algorithm for support vector machines (GA-SVM)[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(Suppl2): 3681-3688. (in Chinese)) |
| [6] |
黎良辉, 魏博文, 徐镇凯. 考虑混凝土坝位移动力突变盲点的安全监控模型[J]. 人民长江, 2013, 44(13): 58-62. ( LI Lianghui, WEI Bowen, XU Zhenkai. Safety monitoring model for concrete dam considering blind spot in dynamic mutation of deformation[J]. Yangtze River, 2013, 44(13): 58-62. DOI:10.3969/j.issn.1001-4179.2013.13.015 (in Chinese)) |
| [7] |
ZHANG Fan, HU Wusheng. Application of neural network merging model in dam deformation analysis[J]. Journal of Southeast University(English Edition), 2013, 29(4): 441-444. |
| [8] |
张俊, 殷坤龙, 王佳佳, 等. 基于时间序列与PSO-SVR耦合模型的白水河滑坡位移预测研究[J]. 岩石力学与工程学报, 2015, 34(2): 382-391. ( ZHANG Jun, YIN Kunlong, WANG Jiajia, et al. Displacement prediction of Baishuihe landside based on time series and PSO-SVR model[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 382-391. (in Chinese)) |
| [9] |
张正虎, 袁孟科, 邓建辉, 等. 基于改进灰色-时序分析时变模型的边坡位移预测[J]. 岩石力学与工程学报, 2014, 33(增刊2): 3791-3797. ( ZHANG Zhenghu, YUAN Mengke, DENG Jianhui, et al. Displacement prediction of slope based on improved grey-time series time-varying model[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(Suppl2): 3791-3797. (in Chinese)) |
| [10] |
何金平, 马传彬, 施玉群. 高拱坝多效应量改进型D-S证据理论融合模型[J]. 武汉大学学报(信息科学版), 2012, 37(12): 1397-1400. ( HE Jinping, MA Chuanbin, SHI Yuqun. Multi-effect quantity fusion model of high arch dam based on improved D-S evidence theory[J]. Geomatics and Information Science of Wuhan University, 2012, 37(12): 1397-1400. (in Chinese)) |
| [11] |
梅泽宇, 许青, 康飞. 基于人工蜂群算法-逐步回归模型的大坝变形监测[J]. 防灾减灾工程学报, 2013, 33(6): 651-656, 670. ( MEI Zeyu, XU Qing, KANG Fei. Dam deformation monitoring based on stepwise regression model with artificial bee colony algorithm[J]. Journal of Disaster Prevention and Mitigation Engineering, 2013, 33(6): 651-656, 670. (in Chinese)) |
| [12] |
周伟, 花俊杰, 常晓林, 等. 水布垭高面板堆石坝运行期工作性态评价及变形预测[J]. 岩土工程学报, 2011, 33(增刊1): 65-70. ( ZHOU Wei, HUA Junjie, CHANG Xiaolin, et al. Estimation of work status and deformation prediction of Shuibuya CFRD[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(Suppl1): 65-70. (in Chinese)) |
| [13] |
魏博文, 熊威, 李火坤, 等. 融合混沌残差的大坝位移蛙跳式组合预报模型[J]. 武汉大学学报(信息科学版), 2016, 41(9): 1272-1278. ( WEI Bowen, XIONG Wei, LI Huokun, et al. Dam deformation forecasting of leapfrog combined model merging residual errors of chaos[J]. Geomatics and Information Science of Wuhan University, 2016, 41(9): 1272-1278. (in Chinese)) |
| [14] |
魏博文, 彭圣军, 徐镇凯, 等. 顾及大坝位移残差序列混沌效应的GA-BP预测模型[J]. 中国科学(技术科学), 2015, 45(5): 541-546. ( WEI Bowen, PENG Shengjun, XU Zhenkai, et al. The GA-BP prediction model considering chaos effect of dam displacement residual[J]. Science China (Technological Sciences), 2015, 45(5): 541-546. (in Chinese)) |
| [15] |
ZHENG K H, WANG Z Q. Application of systematical optimization GM (1, 1) model based on lifting wavelet in dam displacement forecast[J]. Applied Mechanics and Materials, 2014, 488-489(3): 759-764. |
| [16] |
XI G Y, YUE J P, ZHOU B X, et al. Application of an artificial immune algorithm on a statistical model of dam displacement[J]. Computers and Mathematics with Applications, 2011, 62(10): 3980-3986. DOI:10.1016/j.camwa.2011.09.057 |
| [17] |
姜振翔, 徐镇凯, 魏博文. 基于小波分解和支持向量机的大坝位移监控模型[J]. 长江科学院院报, 2016, 33(1): 43-47. ( JIANG Zhenxiang, XU Zhenkai, WEI Bowen. A monitoring model of dam displacement based on wavelet decomposition and support vector machine[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(1): 43-47. DOI:10.11988/ckyyb.20140690 (in Chinese)) |
| [18] |
RANKOVIC ' V, GRUJOVIC ' N, DIVAC D, et al. Development of support vector regression identification model for prediction of dam structural behaviour[J]. Structural Safety, 2014, 48(48): 33-39. |
| [19] |
SU H Z, CHEN Z X, WEN Z P. Performance improvement method of support vector machine-based model monitoring dam safety[J]. Structural Control and Health Monitoring, 2016, 23(2): 252-266. DOI:10.1002/stc.1767 |
| [20] |
李双平, 张斌. 基于小波与谱分析的大坝变形预报模型[J]. 岩土工程学报, 2015, 37(2): 374-378. ( LI Shuangping, ZHANG Bin. Forecast model for dam deformation based on wavelet and spectral analysis[J]. Chinese Journal of Geotechnical Engineering, 2015, 37(2): 374-378. DOI:10.11779/CJGE201502024 (in Chinese)) |
| [21] |
罗德河, 郑东健. 大坝变形的小波分析与ARMA预测模型[J]. 水利水运工程学报, 2016(3): 70-75. ( LUO Dehe, ZHENG Dongjian. Wavelet analysis and ARMA prediction model for dam deformation[J]. Hydro-Science and Engineering, 2016(3): 70-75. (in Chinese)) |
| [22] |
REN F, WU X, ZHANG K, et al. Application of wavelet analysis and a particle swarm-optimized support vector machine to predict the displacement of the Shuping landslide in the Three Gorges, China[J]. Environmental Earth Sciences, 2015, 73(8): 4791-4804. DOI:10.1007/s12665-014-3764-x |
| [23] |
FAN W, QIAO P. Vibration-based damage identification methods: a review and comparative study[J]. Structural Health Monitoring, 2011, 10(1): 83-111. DOI:10.1177/1475921710365419 |
| [24] |
CHENY, OYADIJI S O. Delamination detection in composite laminate plates using 2D wavelet analysis of modal frequency surface[J]. Computers and Structures, 2017, 179: 109-126. DOI:10.1016/j.compstruc.2016.10.019 |
| [25] |
YAN Q, MA C. Application of integrated ARIMA and RBF network for groundwater level forecasting[J]. Environmental Earth Sciences, 2016, 75(5): 1-13. |
| [26] |
SHUMWAY R H, STOFFER D S. Time series analysis and its applications: with R examples[M]. Springer Science and Business Media, 2010.
|
 2018
2018 
