在水利水电工程、矿山工程和核废料填埋工程中,面临着大量的裂隙岩体渗流问题。对裂隙岩体渗流问题认识不清造成过许多重大工程事故,如1959年法国Malpasset拱坝由于坝肩扬压力异常发生溃坝,造成500余人的死亡和300亿法郎的经济损失。裂隙岩体在漫长的地质演化过程中,发展成为多裂隙切割而成的“不连续体”,渗流主要发生在相互连通的裂隙网络中。因此,研究裂隙网络渗流、开发更符合实际情况的裂隙网络渗流模型,具有重要的理论和现实意义。
岩体裂隙系统的几何参数通常通过对野外岩石露头进行统计调查获得。由于采样范围有限,因而获得的裂隙几何参数的分布模型包含了很大的不确定性,为了减少这种不确定性,使之更好地反映真实情况,通常做法是采用离散裂隙网络模型(DFN)[1]来拟合裂隙几何参数的统计分布。
目前运用蒙特卡罗法模拟裂隙网络方面,Dowd等[2]介绍了一种基于高斯结构的新方法,模拟过程中考虑了不同裂隙组之间的空间相关性:Xu等[3]给出了三维裂隙网络模拟技术;李爱华等[4]通过Fortran程序编制了随机裂隙网络模拟程序。目前,离散裂隙网络模型渗流分析方面的研究有待进一步深入。黄勇等[5]应用蒙特卡罗法随机生成裂隙网络系统,基于交叉裂隙网络的流量守恒定理,推导了随机裂隙网络的渗流模型;王晋丽等[6]根据裂隙几何参数分布的统计特性,基于蒙特卡罗模拟技术建立了二维裂隙网络渗流模型,在不同边界条件下分析了二维裂隙网络中的流体流动。Liu等[7]提出了一种代表岩体裂隙网络几何特征的分形模型,将分形特征与裂隙网络的等效渗透率联系起来,使用蒙特卡罗法生成包含分形维数的裂隙网络模型,其尺寸遵循一定幂律分布。
然而,在以往的DFN建模工作中裂隙各几何参数,如裂隙位置、迹长、方向和水力开度等这些参数通常被认为是不相关的。上述研究在模拟随机裂隙网络时也都没有考虑裂隙迹长和开度的相关性,但一些研究人员通过对现场测绘结果的观察推断裂隙的长度和孔径之间存在一定相关关系[8-11],这种相关性对裂隙网络的生成和渗流分析具有重大影响,甚至导致分析结果出现较大误差。鉴于此,本文在传统离散裂隙网络模型基础上,引入裂隙迹线长度和开度的相关性函数,建立一种具有参数相关性的裂隙网络模型,模拟出更符合实际的裂隙场,对随机裂隙网络模型的发展能够有所补充,并基于此分析了两种开度条件下裂隙网络的渗流,对裂隙网络渗流分析具有一定指导意义。
1 裂隙的几何参数和假设 1.1 裂隙位置在DFN数值模拟中裂隙的位置通常被假定为服从泊松分布[12],为了反映裂隙的位置,采用生成服从泊松分布的裂隙中心点来表达,其泊松过程通过基于递归算法生成的随机数来实现,递推公式如下:
| $ {R_{i + 1}} = 27{R_i}-{\rm{INT}}(27{R_i}) $ | (1) |
式中:Ri为[0, 1]之间随机分布的均匀数,INT(x)为取整函数,即取内部函数的x整数部分,初始值R0由线性同余法生成。如果裂隙中心点生成空间定义二维直角坐标系,且范围在[xa1,xa2]和[ya1,ya2]之内,根据直角坐标系的定义,可以生成裂隙中心点坐标(xi,yi),表达式为:
| $ {x_i} = {x_{a1}} + {R_{i + 1}}({x_{a1}}-{x_{a2}}) $ | (2) |
| $ {y_i} = {y_{b1}} + {R_i}({y_{b1}}-{y_{b2}}) $ | (3) |
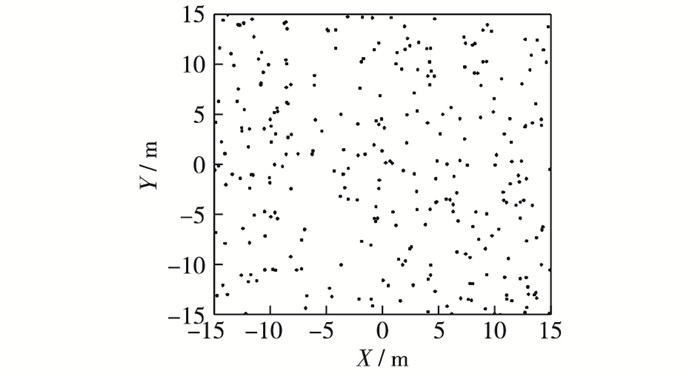
该算法产生裂隙的中心坐标应用于所有正方形DFN模型。图 1为尺寸30 m×30 m的DFN数值模型中裂隙中心点的位置坐标。图中裂隙密度为0.45/m2。
|
图 1 泊松过程确定的裂隙中心位置(案例尺寸30 m×30 m) Figure 1 Locations of fracture center determined by a Poisson process (example at 30 m×30 m scale) |
在野外露头调查过程中,通过分析一些较大规模裂隙的几何特征,文献[13]给出了裂隙迹长按幂律分布的累积概率密度函数:
| $ L = {(L_{_{{\rm{min}}}}^{^{-D}} + F(L_{_{{\rm{max}}}}^{^{-D}}-L_{_{{\rm{min}}}}^{^{ - D}}))^{ - \frac{1}{D}}} $ | (4) |
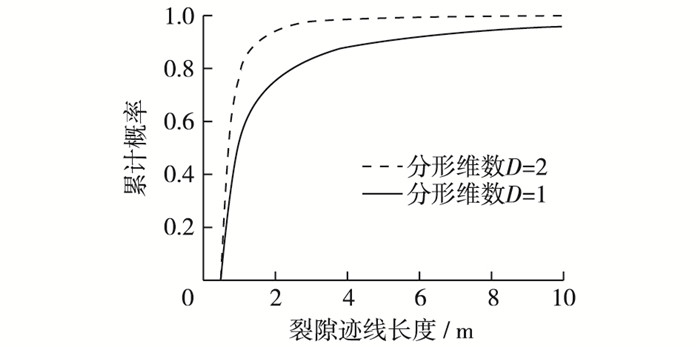
式中:L为裂隙的迹线长度,Lmax和Lmin为最大和最小裂隙迹长,取值范围为0.5~250 m[13],F是区间为[0, 1]的随机均匀分布;D是拟合的分形维数[14],一般取2.2±0.2,图 2显示了随着分形维数D取不同的值,裂隙迹长累积概率曲线的变化,D取值为2,取值1作为比较。
|
图 2 不同分形维数D对裂隙迹线长度的影响 Figure 2 Effects of different fractal dimension D on fracture trace length |
根据文献[12],裂隙走向遵循Fisher分布,这在离散裂隙网络数值建模中被普遍采用,其平均方位角的偏差角累积概率密度函数由下式给出:
| $ \theta = {\rm{co}}{{\rm{s}}^{- 1}}\left\{ {\frac{{{\rm{ln}}[{\rm{exp}}K-F{\rm{ }}({\rm{exp}}K-{\rm{exp}}\left( {-K} \right))]}}{K}} \right\} $ | (5) |
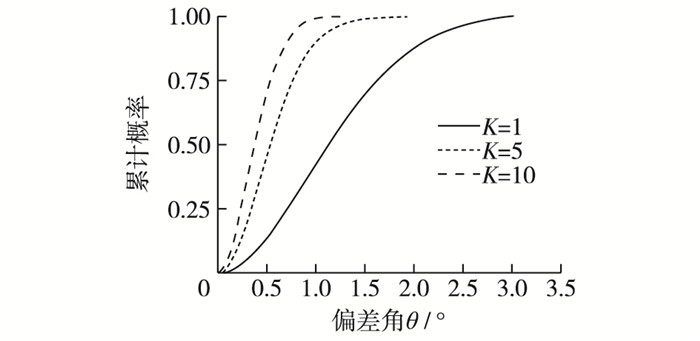
式中:K为Fisher常数;F是区间为[0, 1]的随机均匀分布。由图 3可见,偏差角θ随K变大而减小,当K=10时接近75 %的裂隙走向偏差角θ<0.5 rad,说明区域内某一组裂隙整体走向变异性不大,而当K=1和K=5时,裂隙走向偏差角θ普遍较大,有的甚至达到3 rad,与原走向相反。
|
图 3 不同Fisher常数K对裂隙方位角的偏差角θ的影响 Figure 3 Influences of different Fisher constant K on deviation angle θ of fracture |
假定通过单个裂隙的流体运动遵循立方定律,可以从实验室剪切流试验间接计算出裂隙开度[15]:
| $ h = \sqrt 3 \frac{{12Q\upsilon }}{{gwi}} $ | (6) |
式中:h为裂隙开度; Q为流量(m3/s); w为流道宽度(m); υ为流体运动黏滞系数(m2/s); i为水力梯度; g为重力加速度(m/s2)。为了简化计算,将裂隙开度当作恒定值,根据标准液压试验结果[16-17],裂隙开度服从对数正态分布,其密度函数为:
| $ {f_{{\rm{LN}}}}\left( h \right) = \frac{1}{{\sqrt {2{\rm{ \mathsf{ π} }}} b}}{\rm{exp}}(-{({\rm{ln}}h-a)^2}/(2{b^2})), 0 \le h \le \infty $ | (7) |
式中:a和b为对数正态分布的一阶矩和二阶矩,在使用野外露头调查中的裂隙几何特征数据进行DNF数值模拟时,截断裂隙迹长和开度的分布函数是不能避免的。本文研究中,假设裂隙开度截断分布函数为:
| $ {f_{{\rm{LNTR}}}}\left( h \right) = \frac{{{f_{{\rm{LN}}}}\left( h \right)}}{{\int\limits_{{h_{\rm{a}}}}^{{h_{\rm{b}}}} {{f_{{\rm{LN}}}}} \left( h \right){\rm{d}}h}}, {h_{\rm{a}}} \le h \le {h_{\rm{b}}} $ | (8) |
式中:h为裂隙开度,ha和hb分别为裂隙开度的上下限,分别取为1和200 μm。当开度值小于ha和大于hb时,截断分布函数的值为0。对数正态分布的截断累积分布函数为:
| $ {F_{{\rm{LNTR}}}}\left( h \right) = \int\limits_{{h_{\rm{a}}}}^h {{f_{{\rm{LNTR}}}}} \left( h \right){\rm{d}}h $ | (9) |
经过代数运算,上式可写为:
| $ {F_{{\rm{LNTR}}}}\left( h \right) = (g\left( h \right)-g({h_{\rm{a}}}))/(g({h_{\rm{b}}})-g({h_{\rm{a}}})) $ | (10) |
其中
| $ h = {\rm{exp}}(\sqrt 2 b{\rm{erfinv}}\{ F[g({h_{\rm{b}}})-g({h_{\rm{a}}})] + g({h_{\rm{a}}})\} + a) $ | (11) |
式中:erfinv(x)是逆误差函数; F是[0, 1]之间的随机数。
1.5 裂隙开度与迹长的关系出于简单考虑,裂隙开度与迹线长度通常被假定为不相关。但国外学者在对黏土拉伸变形过程中的断裂模式进行研究时,发现了裂隙的长度和开度的相关性特征[8-11],并提出了裂隙开度与裂隙迹线长度的幂律相关函数:
| $ h = a{l^\beta } $ | (12) |
式中:β为特征指数,其取值为0.5~2.0。通过研究裂隙开度与长度的相关性[11],指出随着裂隙长度和位移的增加, 裂隙的中值宽度趋于增加,裂隙迹长的截断累积概率密度函数可定义为:
| $ {F_{{\rm{LNTR}}}}\left( l \right) = \frac{{{l^{-D}}-l_{_{{\rm{min}}}}^{^{-D}}}}{{l_{_{{\rm{max}}}}^{^{ - D}} - l_{_{{\rm{min}}}}^{^{ - D}}}} = \frac{{g\left( h \right) - g({h_{\rm{a}}})}}{{g({h_{\rm{b}}}) - g({h_{\rm{a}}})}} = F $ | (13) |
式中:Lmax和Lmin为最大和最小裂隙迹长,根据文献[18],将式(13)代入式(11)中,得到了一个基于裂隙开度对数正态分布函数和迹长幂律分布函数的相关函数:
| $ h = {\rm{exp}}(\sqrt 2 b{\rm{erfinv}}\{ (\frac{{{l^{- D}}- l_{_{{\rm{min}}}}^{^{- D}}}}{{l_{_{{\rm{max}}}}^{^{ - D}} - l_{_{{\rm{min}}}}^{^{ - D}}}}[g({h_{\rm{b}}})-g({h_{\rm{a}}})] + g({h_{\rm{a}}})\} + a) $ | (14) |
式中:D为裂隙的分形维数,ha和hb分别为裂隙开度大小的上下限(同式(8)中取值一致),初始值由式(6)给出。因此,a和b可以直接作为输入参数,然后通过式(14)计算出裂隙开度。
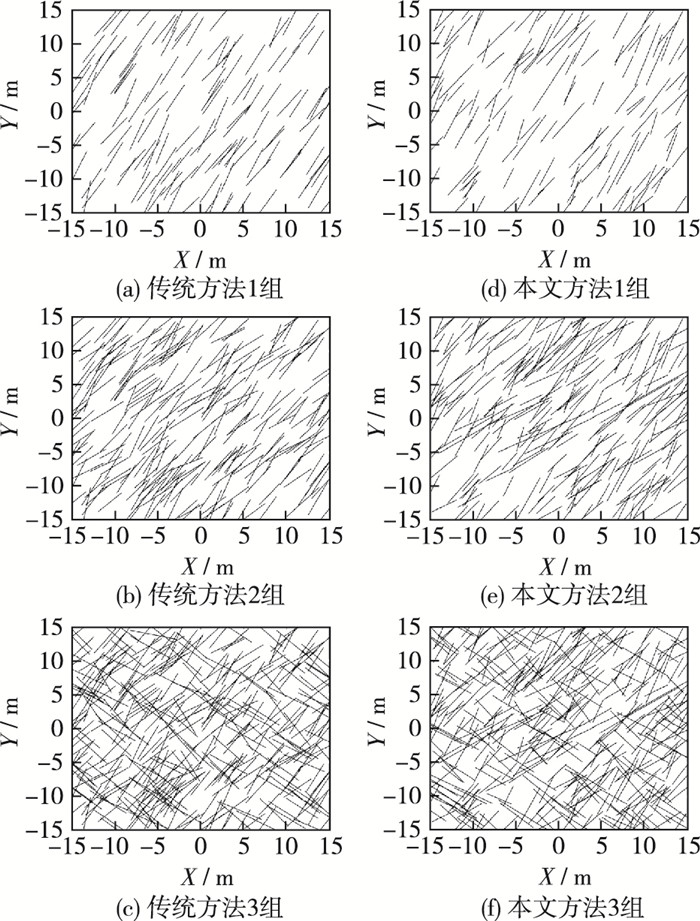
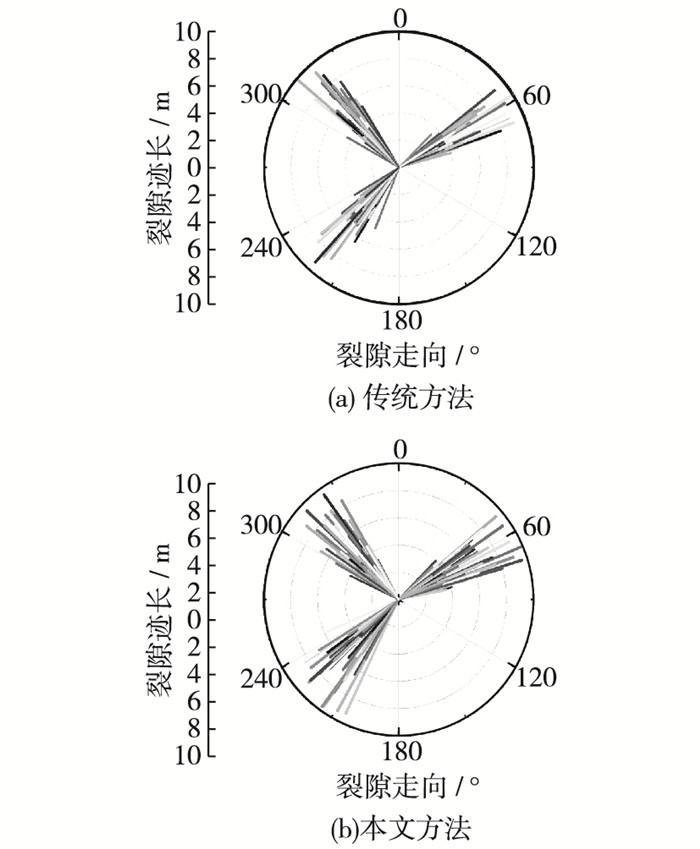
2 随机裂隙网络数值模拟本文研究的裂隙数据源(表 1)基于湖北省黄石市金山店铁矿项目[19]。该矿采用分段崩落法生产,长期开采后在地表形成多个大面积的塌陷区,由于塌陷区相互交叉覆盖,造成大量裂隙贯穿地表,裂隙分布很具有代表性。为了更直观地观察两种裂隙生成方法的不同,基于表 1中裂隙的初始几何参数生成随机裂隙网络,为了消除尺寸效应的影响,采用了统一30 m×30 m的边界尺寸。图 4为文献[19]中传统裂隙生成方法和本文所提出的裂隙生成方法生成的裂隙,可见,传统的随机裂隙网络分布更均匀,这是因为后者通过基于递归算法生成的随机数来实现裂隙的位置,即前一个裂隙位置对后一个裂隙位置的生成有影响,而不像传统裂隙生成方法直接采用随机均匀分布来实现,相应的迹长和走向的玫瑰图如图 5所示,图中显示本文方法生成的裂隙网络中同一裂隙组内的各裂隙走向变异性更大,变化区间尺度大概为30°~35°,而传统方法生成的裂隙网络中同一裂隙组内的各裂隙走向变异性更小,变化区间尺度为25°~30°,因此,裂隙生成方法较传统方法生成了走向变异性更大的裂隙网络,这是因为计算裂隙走向时对结果进行偏差角估计而造成的,从而能够更好地模拟实际地质裂隙随机网络[12]。
| 表 1 裂隙几何参数 Table 1 Fracture parameters used for DFN generation |
|
图 4 随机裂隙网络 Figure 4 Random fracture network |
|
图 5 裂隙迹长和走向的玫瑰图 Figure 5 Fracture trace length and rose diagrams of direction |
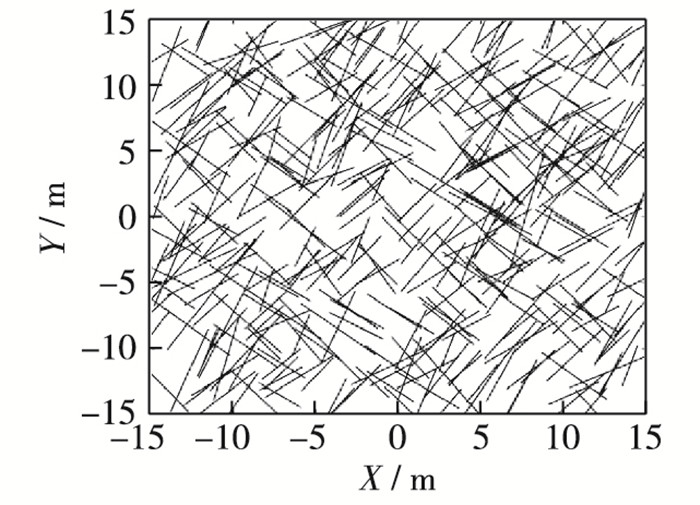
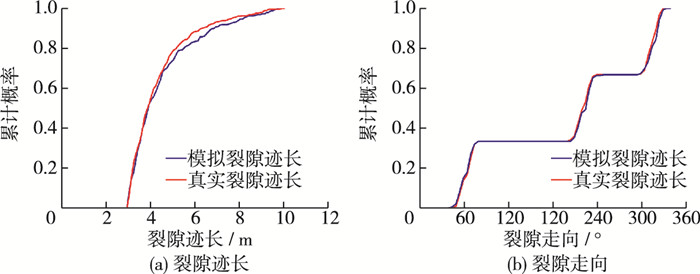
选取的真实裂隙场是通过对裂隙进行现场露头调查,统计分析裂隙几何参数的特性,最后用布尔模拟方法随机生成的一个二维裂隙场[20](图 6)。为了方便比较,真实场的宽度、长度均取为30 m,总裂隙率约为15%。与真实场进行比较时假设所有裂隙的张开度均相同。根据表 1所示统计数据,该裂隙真实场的裂隙走向大致可以分为3组,分别为: 40° ~70°,190°~240°以及290°~330°,而裂隙迹长介于0~12 m。将本文所用方法的模拟结果与真实场统计特征进行比较,对比如图 7,可以看出模拟结果与真实场标准曲线之间拟合效果很好,误差在5%以内。因此,这种随机方法能很好地模拟真实裂隙场,并可应用于后续的裂隙网络渗流分析。
|
图 6 二维真实裂隙场 Figure 6 Two-dimensional real fracture |
|
图 7 裂隙统计特征结果对比 Figure 7 Comparison between statistical characteristics of fracture |
在离散裂隙网络中,岩体中的渗流分布取决于随机网络中裂隙的几何参数和连通率,根据裂隙渗流规律,可知无交叉或者只和1条裂隙交叉的裂隙对渗流没有影响,因此不能作为岩体中的渗流通道,所以在进行裂隙网络渗流分析前要删减和截断那些没有作用的裂隙,提取出随机网络中的连通裂隙,图 8显示了经过净化处理后形成的连通裂隙网络。

|
图 8 二维真实裂隙场 Figure 8 Two-dimensional real fracture |
假定岩块不透水,流体只在连通裂隙中流动。在二维直角坐标系中,对裂隙网络中任一点的总水头,可以定义[21]为:
| $ \phi = z + p/{r_{\rm{w}}} $ | (15) |
式中:z为垂直坐标;p为裂隙中水的压力;rw为水的重度,工程中一般取值为1×104 N/m3。本次研究不考虑裂隙交叉点及裂隙表面粗糙度的影响,假定岩体中单个裂隙的渗流是一维运动。根据Darcy定律,裂隙ij内的流速可表示为
| $ {u_{ij}} =-{k_{ij}}\partial \phi /\partial L $ | (16) |
式中:kij为裂隙ij的渗透系数;L为裂隙迹长。则利用局部立方定律,得到kij-hij函数关系式
| $ {k_{ij}} = {h_{ij}}^2g/\left( {12\upsilon } \right) $ | (17) |
式中:hij为裂隙隙宽;g为重力加速度,一般取值为9.8 m/s2;υ为水的运动黏滞系数,一般取值范围为0.72×10-6~1.516×10-6 m2/s,υ取25°下的近似值0.897×10-6 m2/s。单裂隙内水的流动应满足连续性方程:
| $ \partial {u_{ij}}/\partial L = 0 $ | (18) |
根据质量守恒原理,裂隙交叉点总流量的代数和为0,即
| $ \sum {h_{ij}}{u_{ij}} = 0 $ | (19) |
根据表 1生成DNF模型,采用作者之前开发的裂隙网络渗流计算程序[21],在裂隙网络模型基础上对岩体渗流进行研究。由于在作者之前的研究中对该计算程序已有验证,因此直接采用该方法,而不对其计算合理性进行重复验证。假定模型右侧边界水头为40 m,左侧边界水头为10 m,顶部边界和底部边界均不透水。为了研究裂隙开度与迹长的相关性对岩体裂隙渗透特性的影响,比较两种情况:(1)裂隙的隙宽根据相关性计算式(14)得出;(2)所有裂隙的隙宽为常数65 μm。
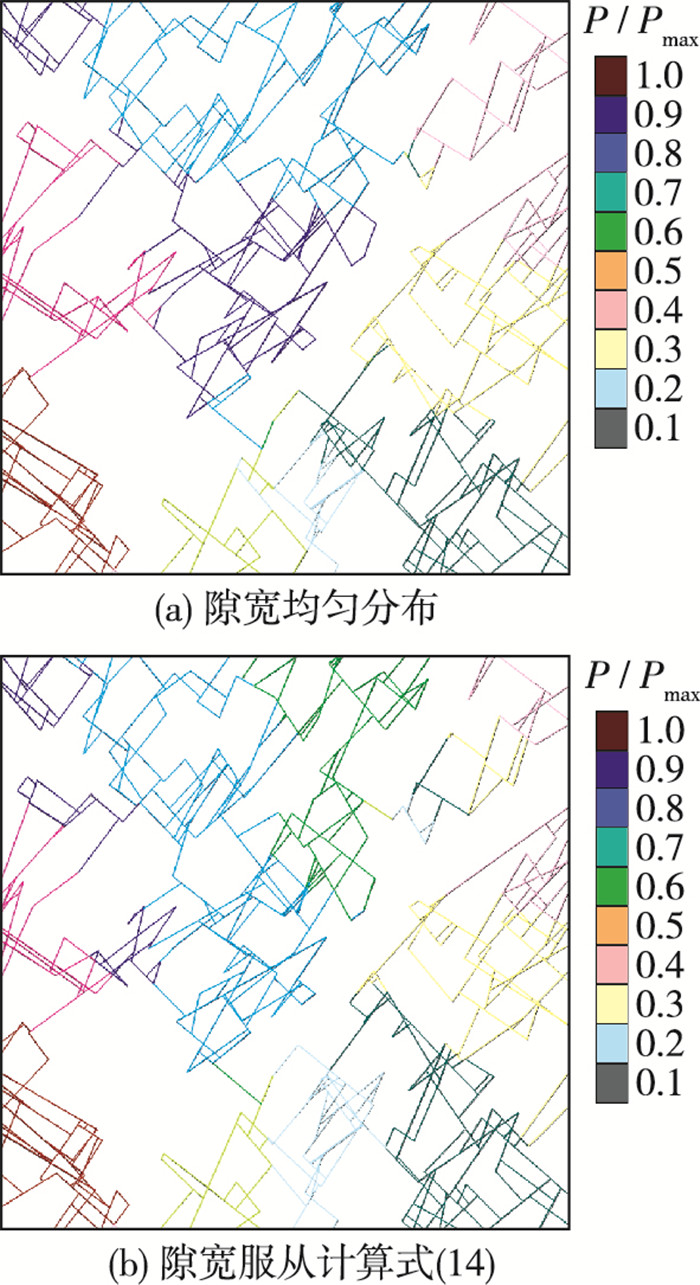
图 9显示了两种不同裂隙开度条件下裂隙网络内部流量分布,图 10给出了裂隙网络模型下游边界裂隙出口的流量分布,可以看出隙宽均匀分布时裂隙网络模型内部及下游出口的流量分布比较均匀,且渗透率较大,而对于裂隙隙宽根据相关性计算式(14)得出的情况,裂隙网络模型内部及下游出口的流量分布差异性较大,优势流路径较为突显,渗流主要由开度较大和迹长较长的裂隙所控制,细小裂隙的流量较小,导水效果很差,图 11给出了裂隙网络内部水压力的分布,裂隙网络左下角的水压力最大,向网络模型右上方向逐步递减,符合渗流水压力规律,证明了程序的有效性。

|
图 9 裂隙网络内部流量分布 Figure 9 Discharge distribution in DFN model |

|
图 10 下游边界出口裂隙流量分布 Figure 10 Discharge distribution in each fracture intersecting left vertical boundary of model |
|
图 11 裂隙网络内部水压力分布 Figure 11 Water pressure distribution in DFN model |
基于蒙特卡罗法,引入裂隙迹线长度和开度的相关性函数,建立了一种新的二维裂隙网络生成算法,并对生成的裂隙网络进行了渗流分析。通过与不考虑相关性的传统随机裂隙网络方法比较,得出以下结论:
(1) 随机裂隙网络生成通过基于递归算法生成的随机数来实现裂隙的位置,取代传统裂隙生成方法中的随机均匀分布,同时对裂隙走向进行偏差角估算,使得裂隙网络分布更符合实际。
(2) 基于黏土拉伸模式中裂隙开度和迹长的幂律相关函数,同时结合裂隙迹长的累积概率密度函数,提出了裂隙开度和迹长的相关函数,使得随机裂隙网络生成更符合物理规律,对随机裂隙网络模型的发展能够有所补充。
(3) 通过将模拟结果与真实场统计特征进行比较,发现模拟结果与真实场标准曲线之间拟合效果很好,误差在5%以内。可见本方法能很好地实现对真实裂隙场的模拟,验证了改进算法的有效性。
(4) 对复杂裂隙网络渗流过程的分析表明,考虑开度和迹长的相关性能反映裂隙网络渗流的结构特征,从而证明了所提方法的合理性。
| [1] |
CUNDALL P A. A computer model for simulating progressive, large scale movement in blocky rock systems[C]//Symp. ISRM, Nancy, France, 1971: 129-136.
|
| [2] |
DOWD P A, XU C, MARDIA K V, et al. A comparison of methods for the stochastic simulation of rock fractures[J]. Mathematical Geology, 2007, 39(7): 697-714. DOI:10.1007/s11004-007-9116-6 |
| [3] |
XU C, DOWD P. A new computer code for discrete fracture network modelling[J]. Computers & Geosciences, 2010, 36(3): 292-301. |
| [4] |
李爱华, 朱江. 基于二维裂隙网络模拟的岩块搜索与岩层追踪方法[J]. 水利水运工程学报, 2014(6): 65-70. ( LI Aihua, ZHU Jiang. A rock block auto-searching and rock layer auto-tracing method based on 2D fracture network simulation[J]. Hydro-Science and Engineering, 2014(6): 65-70. (in Chinese)) |
| [5] |
黄勇, 周志芳. 岩体渗流模拟的二维随机裂隙网络模型[J]. 河海大学学报(自然科学版), 2004, 32(1): 91-94. ( HUANG Yong, ZHOU Zhifang. 2-D stochastic fracture network model for simulation of seepage through fissured rocks[J]. Journal of Hohai University(Natural Science), 2004, 32(1): 91-94. (in Chinese)) |
| [6] |
王晋丽, 陈喜, 黄远洋, 等. 岩体裂隙网络随机生成及连通性研究[J]. 水文地质工程地质, 2013, 40(2): 30-35. ( WANG Jinli, CHEN Xi, HUANG Yuanyang, et al. A study of stochastic generation and connectivity of fracture network in rock mass[J]. Hydrogeology and Engineering Geology, 2013, 40(2): 30-35. (in Chinese)) |
| [7] |
LIU R, JIANG Y, LI B, et al. A fractal model for characterizing fluid flow in fractured rock masses based on randomly distributed rock fracture networks[J]. Computers and Geotechnics, 2015, 65: 45-55. DOI:10.1016/j.compgeo.2014.11.004 |
| [8] |
HATTON C G, MAIN I G, MEREDITH P G. Non-universal scaling of fracture length and opening displacement[J]. Nature, 1994, 367: 160-162. DOI:10.1038/367160a0 |
| [9] |
RENSHAW C E, PARK J C. Effect of mechanical interactions on the scaling of fracture length and aperture[J]. Nature, 1997, 386(6624): 482. DOI:10.1038/386482a0 |
| [10] |
VERMILYE J M, SCHOLZ C H. Relation between vein length and aperture[J]. Journal of Structural Geology, 1995, 17(3): 423-434. DOI:10.1016/0191-8141(94)00058-8 |
| [11] |
STONE D. Sub-surface fracture maps predicted from borehole data: An example from the Eye-Dashwa pluton, Atikokan, Canada[C]//International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts. Pergamon, 1984, 21(4): 183-194.
|
| [12] |
PRIEST S D. Discontinuity analysis for rock engineering[M]. Springer Science and Business Media, 2012.
|
| [13] |
ADLER P M, THOVERT J F. Fractures and fracture networks[M]. Springer Science and Business Media, 1999.
|
| [14] |
周创兵, 熊文林. 不连续面的分形维数及其在渗流分析中的应用[J]. 水文地质工程地质, 1996(6): 1-6. ( ZHOU Chuangbing, XIONG Wenlin. Fractal dimension of discontinuous surface and its application in seepage analysis[J]. Progress in Hydrogeology, 1996(6): 1-6. (in Chinese)) |
| [15] |
MIN K B, JING L, STEPHANSSON O. Determining the equivalent permeability tensor for fractured rock masses using a stochastic REV approach: method and application to the field data from Sellafield, UK[J]. Hydrogeology Journal, 2004, 12(5): 497-510. DOI:10.1007/s10040-004-0331-7 |
| [16] |
DVERSTORP B, ADNERSSON J. Application of the discrete fracture network concept with field data: Possibilities of model calibration and validation[J]. Water Resources Research, 1989, 25(3): 540-550. DOI:10.1029/WR025i003p00540 |
| [17] |
CACAS M C, LEDOUX E, MARSILY G, et al. Modeling fracture flow with a stochastic discrete fracture network: Calibration and validation: 2. The transport model[J]. Water Resources Research, 1990, 26(3): 491-500. |
| [18] |
DE DREUZY J R, DAVY P, BOUR O. Hydraulic properties of two-dimensional random fracture networks following a power law length distribution 2. Permeability of networks based on lognormal distribution of apertures[J]. Water Resources Research, 2001, 37(8): 2079-2095. DOI:10.1029/2001WR900010 |
| [19] |
刘海军. 基于蒙特卡罗法的岩体裂隙网络模型及渗透张量的研究[D]. 哈尔滨: 哈尔滨工业大学, 2011. (LIU Haijun. Studies on discrete fracture network modeling based on Monte-carlo and permeability tensor of rock masses[D]. Harbin: Harbin Institute of Technology, 2011. (in Chinese)) http://www.wanfangdata.com.cn/details/detail.do?_type=degree&id=D260256
|
| [20] |
张弛, 吴剑锋, 陈干, 等. 裂隙网络生成的随机模拟研究[J]. 水文地质工程地质, 2015, 42(4): 12-17. ( ZHANG Chi, WU Jianfeng, CHEN Gan, et al. A comparative study of stochastic modeling for generating fracture networks[J]. Hydrogeology and Engineering Geology, 2015, 42(4): 12-17. (in Chinese)) |
| [21] |
姚池, 姜清辉, 叶祖洋, 等. 裂隙网络无压渗流分析的初流量法[J]. 岩土力学, 2012, 33(6): 1896-1903. ( YAO Chi, JIANG Qinghui, YE Zuyang, et al. Initial flow method for unconfined seepage problems of fracture networks[J]. Rock and Soil Mechanics, 2012, 33(6): 1896-1903. (in Chinese)) |
 2018
2018 
