2. 河海大学 水利水电学院,江苏 南京 210098
水工闸门结构振动是水利工程中普遍存在的问题[1-3]。闸门在动水荷载作用下运行时,难免会遇到动压力的“水锤效应”,这种流固耦合现象可能会引起闸门结构振动特性的变化,对其结构的动力稳定产生不利影响[4-5]。运用动力特性分析方法研究闸门在动水荷载作用下的动力响应、动力稳定性及安全可靠性具有重要意义[6-7]。但由于问题的复杂性,闸门结构的动力设计目前还没有统一标准[1, 8-9]。某水闸工程金属结构设备包括工作闸门、埋件、启闭机和锁定设备以及检修叠梁。因该工作闸门是一种新水工门型,且体型尺寸大,接近超大型弧形闸门,闸门启闭及运行过程中闸下水流条件复杂,闸门常受门底泄流所形成的水流漩滚的冲击作用。闸门启闭及局部开启运行条件下的水流动力荷载以及水流脉动引起的闸门振动将直接影响闸门的安全运行。基于此,通过数值仿真计算方法,研究了该闸门结构的动力特性。
1 工程概况某新型闸门门叶为弧面和平面围成的封闭空箱。门叶固定在闸门两侧的支撑结构上,支撑结构与支铰相连,支铰固定在闸墩内,在液压启闭机操作下,闸门绕支铰旋转。弧形钢闸门宽22 m,高7.76 m,正向挡水时最大设计总水压力约2 307 kN,反向挡水时最大设计总水压力约5 404 kN。闸门由门叶、两侧圆盘形支撑结构和支铰组成,质量为230 t。门叶为焊接的钢结构。面板布置在江侧,面板外缘弧面半径为5.5 m,沿门叶高度方向布置若干横梁以及纵隔板及横肋,门叶最大厚度1.71 m。门叶两端与支撑结构相连,为防止支撑结构突出闸墩,将支撑结构设置在闸墩内的圆形壁龛内,壁龛深1.0 m。闸门两侧的支撑圆盘为焊接结构,圆心处设置闸门支铰,高程为2.775 m,支铰设计成全密封结构并采用自润滑关节轴承。为了简化水工体型,将支铰轴用螺栓固定在焊接钢制圆筒上,预埋在闸墩二期混凝土内。门叶底、侧止水均采用V形水封橡皮;在闸门侧面,上下各设置一个弹性侧轮,用于保证闸门平稳启闭。止水面采用不锈钢。水闸平面布置见图 1,翻转式弧形门向下开启时闸门状态见图 2。

|
图 1 水闸平面布置 Figure 1 Sluice layout |

|
图 2 翻转式弧形门向下开启时闸门状态 Figure 2 Gate condition with inverted arc door opened downward |
水工闸门结构的动力特性参数(模态参数)主要包括自振频率、振型及阻尼等[10]。其中,自振频率是引起闸门产生共振的主要不利因素,因自振频率和振型相互对应,阻尼对闸门结构的影响不大[11],所以实际工程中,一般不考虑阻尼力的影响。参考文献[12]中无阻尼自由振动方程:
| $ \mathit{\boldsymbol{M\ddot \delta }} + \mathit{\boldsymbol{K\delta }} = 0 $ | (1) |
式中:M, K分别为质量矩阵和刚度矩阵;
闸门自由振动可以看成是一系列简谐振动的叠加,设这种简谐振动为:
| $ \mathit{\boldsymbol{\delta }} = \mathit{\boldsymbol{\phi }} \cos\omega t $ | (2) |
式中:ϕ为加速度振幅;ω为简谐振动频率。
将式(2)代入式(1),可得到如下的齐次方程:
| $ \left( {\mathit{\boldsymbol{K}}-\omega _{_i}^{^2}\mathit{\boldsymbol{M}}} \right){\boldsymbol{\phi} _i} = 0 $ | (3) |
式中: ωi (i=1, 2, …, n)为n个自由度的闸门对应的n个自振频率,又称为闸门结构的特征值;ϕi为i阶自振频率对应的振型,又称为特征向量。
闸门自由振动时,闸门结构中各节点的振幅ϕi不全为零,所以式(3)中括号内矩阵的行列式值必为零,由此可以得到闸门自振频率的方程为:
| $ \left| {\mathit{\boldsymbol{K}}-\omega _{_i}^{^2}\mathit{\boldsymbol{M}}} \right| = 0 $ | (4) |
式(4)是关于ωi2的n次代数方程,因而可解出结构的n个自振频率。对于每个自振频率,由式(3)可以确定一组各节点的振幅值φij= [ϕi1, ϕi2, …, ϕin]T,它们之间保持固有的比值,但绝对值可以任意变化。
2.2 附加质量的模拟附加质量是Westergaard在对水体-坝体基础上提出的一种考虑水体对结的作用的一种简化计算方法[12-13]。由于闸门可以看成是一种特殊的可移动坝体,因此根据Westergaard附加质量公式[14-15]编制了相应的子程序模拟附加质量的作用,施加到结构挡水面相应的节点上。
3 有限元建模 3.1 闸门有限元模型在建立闸门结构三维有限元模型时,取x轴方向指向水流方向,y轴方向垂直水流方向指向河流的左岸,z轴垂直指向上方,所采用的坐标系符合笛卡尔坐标系右手螺旋法则。壳单元的局部坐标系与整体坐标系的转换如下:将固定坐标系平移到壳单元表面,x投影到表面上的即为局部坐标系x轴,法线方向即为z方向,用右手螺旋法则确定y方向。若x轴与平面夹角较小,则取固定坐标系z轴投影到面上为局部坐标系x轴。
闸门结构面板(弧形面板、直面板)、主横梁、纵向隔板、两侧面板、两侧支板、腹板均采用空间任意四边形板壳单元模拟;闸门支铰、转轮和吊耳均采用8节点六面体单元模拟。水闸计算模型节点总数为83 729,单元总数为85 411,其中8节点实体单元总数为3 336,4节点面单元总数为82 075。动力计算时,在支铰处施加法向约束,环向可自由转动,并约束与液压杆启闭机连接处的吊点。水闸闸门结构整体模型网格见图 3。

|
图 3 闸门结构整体模型网格 Figure 3 Model mesh of sluice gate structure |
进行闸门动力分析时,考虑结构的自重和内河、外河水脉动压力的作用。水闸脉动压力试验共设置了15个测点,弧形面板8个测点,直面板7个测点(图 4)。以高程z为自变量,以脉动压力值为因变量,在弧形面板、直面板上分别找几个不同高程的测点,分段线性拟合脉动压力与高程的关系式。通过Fortran语言编写脉动压力线性插值子程序,利用商业有限元软件ABAQUS的二次开发功能pressure/User-defined,将模型试验测定离散的水流脉动压力数据转化为作用在闸门上的水动力荷载。

|
图 4 闸门脉动压力试验测点布置 Figure 4 Layout of measured points for gate fluctuating pressure |
边界条件为:吊耳处(与液压启闭机连接的吊耳)约束x,y,z方向;支铰内部建立局部坐标系,法向约束支铰,吊点处固定坐标约束x,y(以支铰的圆心(0, 0, 2.775)为坐标原点,在该铰平面内找两个点确定局部柱坐标)。
3.3 计算参数闸门选用的钢材为Q345(16Mn, 16Mnq)钢,其容许应力[1]对应的闸门面板厚度介于(40~63]之间。计算模型参数如下:钢材的容许应力σ为220 MPa,抗剪强度τ为130 MPa,局部承压σcd为330 MPa,密度ρ为7 850 kg/m3,弹性模量E为210 GPa,泊松比μ为0.296 3。
3.4 计算工况(1) 自振特性分析工况 自振特性在计算过程中主要考虑以下2个工况:工况1,不考虑流固耦合时该水闸结构的自振特性分析;工况2,考虑流固耦合的起吊工况下不同开度(门顶高程3.5,2.5,1.5和0.5 m)时的自振特性分析。
(2) 动力计算工况 由于闸门结构的自振频率代表了结构振动的内因,下面应用前述附加质量模拟考虑了水体对结构的影响,求解闸门在不同开度起吊工况下的自振特性。闸门动力计算工况见表 1。
| 表 1 动力计算工况 Table 1 Dynamic calculation working conditions |
通过建立Linear perturbation线性摄动分析步,进行了考虑和不考虑水流作用的自振特性分析。
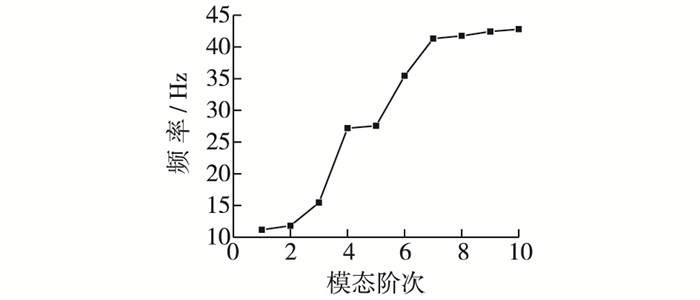
挡水工况下不考虑水流作用的闸门自振频率变化曲线(无水)见图 5,闸门不同开度下自振频率变化曲线(有水)见图 6。
|
图 5 闸门结构自振频率变化曲线(无水) Figure 5 Variation of natural frequency of sluice gate structure (anhydrous) |
|
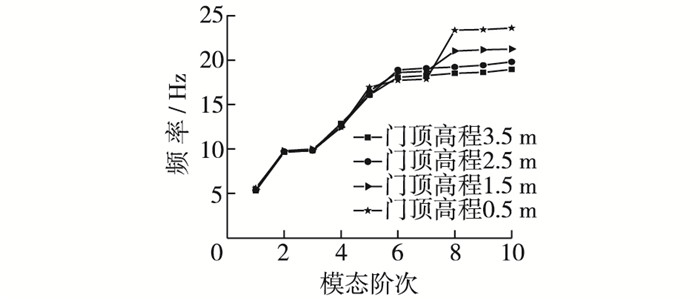
图 6 闸门不同开度下自振频率变化曲线(有水) Figure 6 Variation of natural frequency under different opening of sluice gate |
由计算结果可以看出:闸门自振的基频比较高,不计水体作用挡水工况下,基频为11.188 Hz,考虑水体影响,不同开度下分别为5.284 4,5.338 3,5.461 6和5.598 4 Hz。一般而言,在考虑流固耦合作用下,自振频率较不考虑流固耦合效应均有所降低。由于闸门双向挡水,而且门顶还要溢流,流固耦合效应对闸门基频的影响较大。闸门向下开启时,随着开度的增大(门顶高程减小),闸门的自振频率有所增加。
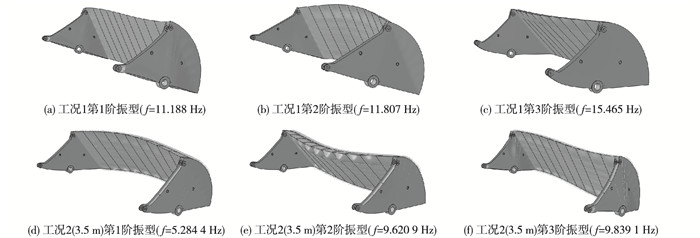
4.2 振型分析由于高阶频率对结构的动响应贡献较小,这里只展示典型工况下前3阶的振型图(见图 7)。由于工况2不同开度情况下较多,这里只展示门顶高程3.5 m开度下考虑水体影响的前3阶振型图。
|
图 7 典型工况下前3阶的振型 Figure 7 First three order vibration mode diagrams of typical working conditions |
由计算结果可知,工况1第1阶振型闸门沿着横河向扭动,第2阶振型闸门挡水面板整体向外河外凸,第3阶振型闸门面板整体向内河外凸,吊耳向上扭曲;工况2(3.5 m)第1阶振型挡水面板整体向外河外凸,吊耳向上扭曲;第2阶振型闸门面板整体向内河外凸,吊耳向上扭曲;第3阶振型闸门沿着横河向扭动。
5 脉动压力频谱分析各工况试验所用时间为12 s,采用时间步长为0.007 812 5 s,几何比尺为20,根据重力相似准则可知,压强比尺为20。由水闸各测点脉动压力时程试验数据分析发现,弧形面板、直面板的测点脉动压力测值在同一高程的脉动压力值基本相同。
根据频谱分析理论,对水流脉动压力时域曲线进行频谱分析,功率谱图中的纵坐标用相对值表示,主要是为了显示优势频率所在位置。在功率谱图中随图给出了优势频率的大小。由计算结果可知高程较低测点的脉动压力试验值较大,脉动压力的优势频率主要处在0.3~1 Hz,10~20 Hz,30~50 Hz。由于工况较多,这里给出了工况1典型测点的脉动压力时域曲线和功率谱曲线,由图 8可见,测点11和6的优势频率是15.979 Hz。

|
图 8 不同测点脉动压力时域曲线和功率谱曲线 Figure 8 Pulse pressure time domain curves and power spectrum curves of different measuring points |
由结构动力学可知,当结构的自振频率与激励频率接近时,结构可能产生危险性振动,一般认为两者错开20%以上时,就不会发生危害性振动。闸门在工况1下考虑流固耦合的闸门自振频率前5阶为5.284 4, 9.620 9, 9.839 1,12.865 0,16.073 0 Hz,在频率为12.865和16.073 Hz的激励荷载作用下,可能产生共振,但是高阶频率对结构的动响应贡献较小,即使与激励频率接近,结构的动响应一般也不会很大,不会产生危害性破坏。
6 结构动力计算结果根据Westergaard附加质量公式[11-12]编制了相应的子程序模拟附加质量的作用,施加到结构挡水面相应的节点上来计算水流对闸门结构的影响。采用时程分析方法,求解闸门结构在脉动水流作用下各个工况闸门各个构件的动位移动应力及其分布。由于增量步较多,根据odb结果文件去找出各个部件的应力、位移最大值,工作量太大,因此编写了结果处理程序。能快速方便地找出各个单元节点所有分析步中应力、位移的最值。
6.1 闸门结构动位移计算分析根据上述各个工况的不同情况,重点挑出6种不同代表性的危险工况予以研究,即3种水位下的最大开度及最小开度。工况1,工况4,工况5,工况7,工况8,工况10。对闸门结构的动位移进行计算。典型工况1弧形面板的x向、y向、z向位移云图,其分布规律分别见图 9。通过对闸门结构的动位移计算,得到总动位移统计结果见表 2。

|
图 9 工况1弧形面板位移云图 Figure 9 Displacement nephogram of arc panel of working condition 1 |
| 表 2 闸门各构件位移最大值及所在工况 Table 2 Maximum displacements of each component of gate and corresponding working conditions |
由表 2可见,闸门x向最大位移25.1 mm,出现在工况5(内河挡水位3.5 m,外河挡水位1.03 m,闸门门顶高程为2.5 m)直面板的下部中间位置;y向最大位移为4.9 mm,出现在工况4(内河挡水位4.1 m,外河挡水位2.15 m,闸门开度门顶高程为0.5 m)两侧面板与弧形面板接缝附近中部。z向最大位移为38.1 mm,发生在工况4的弧形面板上部中间位置。
6.2 闸门结构动应力计算分析根据上述各个工况的不同情况,对闸门结构的动应力进行计算,计算结果见表 3。
| 表 3 所有工况闸门各构件应力最值及其所在工况 Table 3 Maximum and minimum stress of gate components and corresponding working conditions |
由表 3可见,平面正应力最大值为320.267 MPa,表现为y向平面压应力,出现在工况4(内河挡水位4.1 m,外河挡水位2.15 m,闸门开度门顶高程为0.5 m)翼缘边缘拐角处;工况5(内河挡水位3.5 m,外河挡水位1.03 m,闸门开度门顶高程为3.5 m)翼缘边缘拐角处出现y向平面正应力253.133 MPa,工况8横肋处出现x向压应力242 MPa。最大平面剪应力为269.675 MPa,出现在工况5吊耳处。稍微超出材料允许强度,其他部件均满足强度要求。
7 结语本文基于随机振动分析方法对某水工弧形空腔闸门进行结构动力数值仿真分析。研究了该大尺寸新型闸门结构的动力特性,评价了其振动安全性,主要研究内容和结果如下:
(1) 取得了闸门自振的基频等模态参数,不计水体作用挡水工况下,基频为11.188 Hz,考虑水体影响,不同开度下分别为5.284 4~5.598 4 Hz。一般而言,在考虑流固耦合作用下,自振频率较不考虑流固耦合效应均有所降低。这是由于闸门双向挡水,而且门顶还要溢流,流固耦合效应对闸门基频的影响较大。闸门向下开启时,随着开度的增大(门顶高程减小),闸门自振频率有所增加。
(2) 根据频谱分析理论,对水流脉动压力时域曲线进行了频谱分析,发现弧形面板、直面板的测点脉动压力测值在同一高程的脉动压力值基本相同,但在门宽方向会存在相位差,因此在闸门振动响应计算时,脉动压力荷载的输入可能对计算结果的影响较大,进一步研究中会考虑脉动压力的相位差影响。
(3) 闸门各构件位移最大值出现的最不利工况分别为工况5和4;各构件应力最大值所在的工况分别为工况4,5和8。其中闸门结构局部应力较大,超出结构容许应力,需对闸门结构进行修改优化,否则结构局部强度不满足要求,其他部件均满足强度要求。
| [1] |
SL74-2013水利水电工程钢闸门设计规范[S]. (SL74-2013 Specification for design of steel gate in hydraulic and hydroelectric engineering[S]. (in Chinese))
|
| [2] |
张维杰, 严根华, 陈发展, 等. 深孔弧形闸门静动力特性及流激振动[J]. 水利水运工程学报, 2016(2): 111-119. ( ZHANG Weijie, YAN Genhua, CHEN Fazhan, et al. Static and dynamic characteristics of high pressure radial gate and its flow-induced vibration[J]. Hydro-Science and Engineering, 2016(2): 111-119. (in Chinese)) |
| [3] |
辛华荣, 王建, 严根华, 等. 大型平面有轨对拉式弧形闸门流激振动特性及抗振措施[J]. 水利水运工程学报, 2012(6): 87-94. ( XIN Huarong, WANG Jian, YAN Genhua, et al. Flow-induced vibration characteristics of large and flat rail pull radial gate and vibration control measures[J]. Hydro-Science and Engineering, 2012(6): 87-94. (in Chinese)) |
| [4] |
钱声源, 田宏吉, 王家骐, 等. 某在役弧形闸门不平衡启门力数值分析研究[J]. 人民长江, 2015, 46(22): 83-87, 94. ( QIAN Shengyuan, TIAN Hongji, WANG Jiaqi, et al. Numerical analysis of imbalanced uplifting force of an arc gate in service[J]. Yangtze River, 2015, 46(22): 83-87, 94. (in Chinese)) |
| [5] |
刘计良. 高水头弧形钢闸门主框架强度及动力稳定性分析方法研究[D]. 杨凌: 西北农林科技大学, 2015. (LIU Jiliang. Study on analysis methods for strength and dynamic stability of the main frames of steel radial gates with high water head[D]. Yangling: Northwest Agriculture and Forestry University, 2015. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10712-1015333662.htm
|
| [6] |
庞崇安, 王震. 大型弧形闸门的水下爆破冲击荷载及动力响应分析[J]. 水力发电, 2017, 43(6): 80-84, 114. ( PANG Chong'an, WANG Zhen. Analysis of underwater blasting shock loading and dynamic response of large scale radical gate[J]. Water Power, 2017, 43(6): 80-84, 114. (in Chinese)) |
| [7] |
陈琼, 李云, 刘本芹, 等. 高水头船闸一字闸门水动力特性数值模拟[J]. 水利水运工程学报, 2017(1): 87-94. ( CHEN Qiong, LI Yun, LIU Benqing, et al. Numerical simulation of hydrodynamic characteristics of single-leaf gate of high-head navigation lock[J]. Hydro-Science and Engineering, 2017(1): 87-94. (in Chinese)) |
| [8] |
张林让, 蒋昱州, 曾平, 等. 向家坝导流底孔平面封堵闸门流激振动问题研究[J]. 长江科学院院报, 2011, 28(10): 186-192. ( ZHANG Linrang, JIANG Yuzhou, ZENG Ping, et al. Study on flow-induced vibrations of the slide plane gate at the bottom outlet of Xiangjiaba Dam[J]. Journal of Yangtze River Scientific Research Institute, 2011, 28(10): 186-192. DOI:10.3969/j.issn.1001-5485.2011.10.033 (in Chinese)) |
| [9] |
蒋寅军, 宋一乐, 王朝晖, 等. 乌江思林水电站溢流坝弧形工作闸门流激振动试验[J]. 武汉大学学报(工学版), 2010, 43(4): 467-471. ( JIANG Yinjun, SONG Yile, WANG Zhaohu, et al. Experiment of fluid-induced vibration at spillway radial gate of Silin Hydropower Station at Wujiang river[J]. Engineering Journal of Wuhan University, 2010, 43(4): 467-471. (in Chinese)) |
| [10] |
严根华, 陈发展. 涌潮荷载作用下大型桁架式平面闸门动力响应仿真分析[J]. 水利水电科技进展, 2010, 30(3): 42-46, 57. ( YAN Genhua, CHEN Fazhan. Simulation of dynamic responses of large truss-plane gates under tidal surge loads[J]. Advances in Science and Technology of Water Resources, 2010, 30(3): 42-46, 57. DOI:10.3880/j.issn.1006-7647.2010.03.011 (in Chinese)) |
| [11] |
顾云, 严根华, 赵建平. 上卧式闸门水弹性振动试验研究[J]. 振动、测试与诊断, 2009, 29(3): 333-339, 373. ( GU Yun, YAN Genhua, ZHAO Jianping. Hydro-elastic vibration test of a lying-up gate[J]. Journal of Vibration, Measurement & Diagnosis, 2009, 29(3): 333-339, 373. (in Chinese)) |
| [12] |
姬锐敏. 长沙枢纽弧形闸门静动力特性研究[D]. 长沙: 长沙理工大学, 2013. (JI Ruimin. Static and dynamic characteristics research for Changsha hub radial gate[D]. Changsha: Changsha University of Science & Technology, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10536-1013300410.htm
|
| [13] |
李火坤, 练继建. 水工弧形闸门流激振动特性物模-数模联合预测与安全分析[J]. 水力发电学报, 2007, 26(3): 69-76. ( LI Huokun, LIAN Jijian. Joint prediction and safety analysis of the flow-induced vibration of hydraulic radial gate using physical and numerical model[J]. Journal of Hydroelectric Engineering, 2007, 26(3): 69-76. (in Chinese)) |
| [14] |
王均星, 焦修明, 陈炜. 龙滩工程底孔弧形闸门的自振特性[J]. 武汉大学学报(工学版), 2008, 41(5): 31-34. ( WANG Junxing, JIAO Xiuming, CHEN Wei. Free vibration characteristics of bottom outlet radial gate for Longtan project[J]. Engineering Journal of Wuhan University, 2008, 41(5): 31-34. (in Chinese)) |
| [15] |
徐磊. 基于ABAQUS的四节点三维附加质量单元开发[J]. 水电能源科学, 2011, 29(6): 100-102. ( XU Lei. Development of four nodes 3-D added mass element in ABAQUS[J]. Water Resources and Power, 2011, 29(6): 100-102. (in Chinese)) |
2. College of Water Conservancy and Hydropower Engineering, Hohai University, Nanjing 210098, China
 2018
2018 