2. 江苏省水利厅,江苏 南京 210029
我国很多入海河口建有挡潮闸,用以挡潮蓄淡、排洪除涝和抵挡风暴潮。潮汐河口建闸也使得闸下河段动力环境发生改变。由于受到闸门反射作用,闸下河段上溯潮波由前进波转为驻波,与此同时,上溯潮波沿程不断受到底摩擦、地形变浅等影响,产生明显变形[1-2]。其中,地形影响产生的潮汐涨落潮不对称性和闸下反射作用产生的驻波因对闸下潮汐水流运动和泥沙输运产生明显影响,被很多研究者解释为闸下淤积的重要原因之一[3-4]。然而,对于闸下河段风暴潮传播会不会产生与潮波传播类似的变形,闸下风暴潮水位是否存在类似变化,目前关注相对较少。由于风暴潮预警一般针对沿海岸地区至河口及口内,因此关注闸下风暴潮变化对于风暴潮防护、防洪排水等具有实际意义。
江苏沿海地区风暴潮频发,风暴期间外海水位抬升,河口地区暴雨汇流和上游径流向海排洪受阻,极易产生河口地区的洪涝灾害。苏北沿海地势低洼,入海河流众多、河口挡潮闸密集,其中以里下河地区最为突出。里下河地区河网密布,地势极低,历史上洪水灾害时有发生。境内主要排水通道有射阳河、黄沙河、新洋河和斗龙河,下游分别设置射阳河闸、新洋河闸、黄沙河闸、斗龙河闸、大丰闸等大小挡潮闸10余座,承担着地区引水灌溉、防洪排涝、通航运输等任务。本文在江苏沿海风暴潮模型基础上,建立里下河地区风暴潮数学模型,以“9711”台风风暴潮为例,计算分析射阳河、新洋河和斗龙河闸下风暴潮水位的变化,并与潮汐水位变化进行比较,分析风暴潮波传播变形与潮波变形的异同;并在此基础上模拟外海风暴潮对闸下排洪过程的影响,为建闸河口防洪排水提供理论参考。
1 模型简介 1.1 基本方程在笛卡尔坐标系下,采用静压假定、刚盖假定和Boussineq近似,并认为水流垂线不均匀分布产生的积分修正系数为1.0,描述水流基本运动方程的Navier-Stokes方程可简化为沿水深平均的平面二维浅水方程:
| $ ~\frac{\partial h}{\partial t}+\frac{\partial h\bar{u}}{\partial x}+\frac{\partial h\bar{v}}{\partial y}=0 $ | (1) |
| $ \begin{align} &\frac{\partial h\bar{u}}{\partial t}+\frac{\partial h{{{\bar{u}}}^{2}}}{\partial x}+\frac{\partial h\bar{v}\bar{u}}{\partial y}=f\bar{v}h-gh\frac{\partial \eta }{\partial x}-\frac{h}{{{\rho }_{0}}}\frac{\partial {{p}_{\text{a}}}}{\partial x}+ \\ &\frac{1}{{{\rho }_{0}}}~\left( {{\tau }_{\text{s}x}}-{{\tau }_{\text{b}x}} \right)-\frac{1}{{{\rho }_{0}}}\left( \frac{\partial {{S}_{xx}}}{\partial x}+\frac{\partial {{S}_{xy}}}{\partial y} \right)+\frac{\partial }{\partial x}\left( h{{T}_{xx}} \right)+\frac{\partial }{\partial y}\left( h{{T}_{xy}} \right) \\ \end{align} $ | (2) |
| $ \begin{align} &\frac{\partial h\bar{v}}{\partial t}+\frac{\partial h\bar{u}\bar{v}}{\partial x}+\frac{\partial h{{{\bar{v}}}^{2}}}{\partial y}=-f\bar{u}h-gh\frac{\partial \eta }{\partial y}-\frac{h}{{{\rho }_{0}}}\frac{\partial {{p}_{\text{a}}}}{\partial y}+ \\ &\frac{1}{{{\rho }_{0}}}~\left( {{\tau }_{\text{s}y}}-{{\tau }_{\text{b}y}} \right)-\frac{1}{{{\rho }_{0}}}\left( \frac{\partial {{S}_{yx}}}{\partial x}+\frac{\partial {{S}_{yy}}}{\partial y} \right)+\frac{\partial }{\partial x}\left( h{{T}_{yx}} \right)+\frac{\partial }{\partial y}\left( h{{T}_{yy}} \right) \\ \end{align} $ | (3) |
式中:h=η+d为总水深,η为潮位,即以参考基面为准的水面位置,d为海底到参考基面的距离;u,v分别为x,y方向垂线平均流速;t为时间;f为科氏系数, f=2ωsinφ,ω为地球自转的角速度,φ为所在地区的纬度;g为重力加速度;pa为大气压;ρ0为水体密度;τsx,τsy为水体表面风应力项;τbx,τby为底部摩擦项;Sxx,Sxy,Syx,Sxx为波浪辐射应力分量[5]。
水体表面风应力项表示为:
其中:ρa为空气密度;W10为海面10 m风速;W10x,W10y分别为x,y方向上的分量;cd为风应力系数。
底部摩擦项表示为:
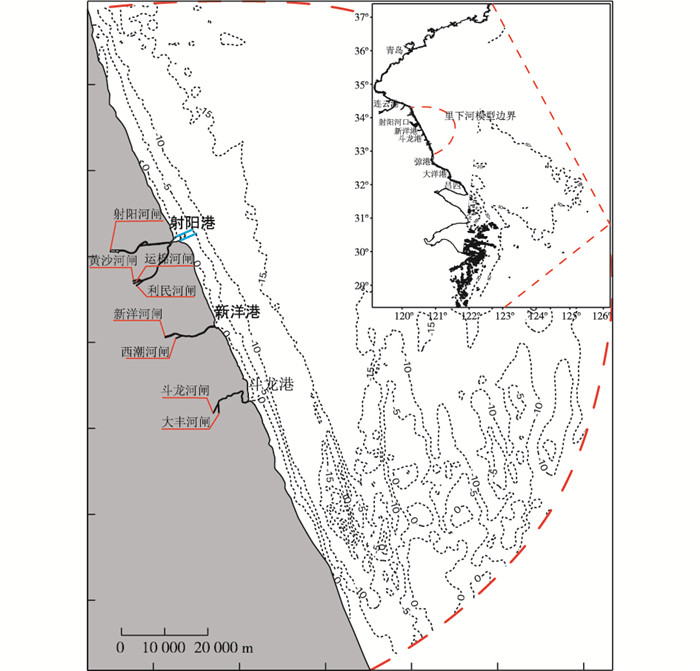
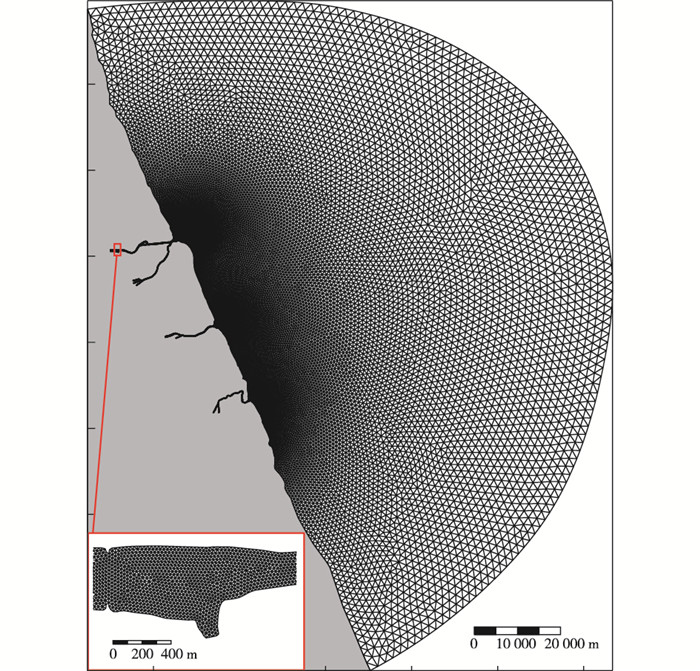
风暴潮模型采用大-中-小模型嵌套的方法。大模型为西北太平洋风暴潮模型[6],模型范围90°E~160°E,0°N ~60°N;大模型计算提供中模型边界条件。中尺度模型为江苏沿海模型(图 1),采用球坐标下的Adcirc模式[7];模型为局部模型提供边界条件。里下河局部模型范围见图 1,上游边界取在闸门附近位置,下游边界在外海距离河口约50 km。网格采用非均匀三角形网格,局部闸门网格在10 m左右,外海边界网格在1 000 m左右(见图 2)。模型采用Mike 21水流计算模块进行计算,其中闸门过流模拟采用模块中的gate建筑物模拟(表 1,85国家高程基面,下同),参数选取参考表 1(将航孔进行合并)。计算闸下水位变化时,将闸门关闭;研究排水影响时,将闸门开启。计算时紊动扩散系数采用Smagorinsky公式计算(系数为0.28),底部曼宁系数根据经验取为1/60。
|
图 1 中尺度风暴潮模型和局部数学模型范围 Figure 1 Domains of middle-scale storm surge model and local model |
|
图 2 局部模型网格 Figure 2 Meshs of local model |
| 表 1 各闸门尺寸参数 Table 1 Size parameters of sluice gate |
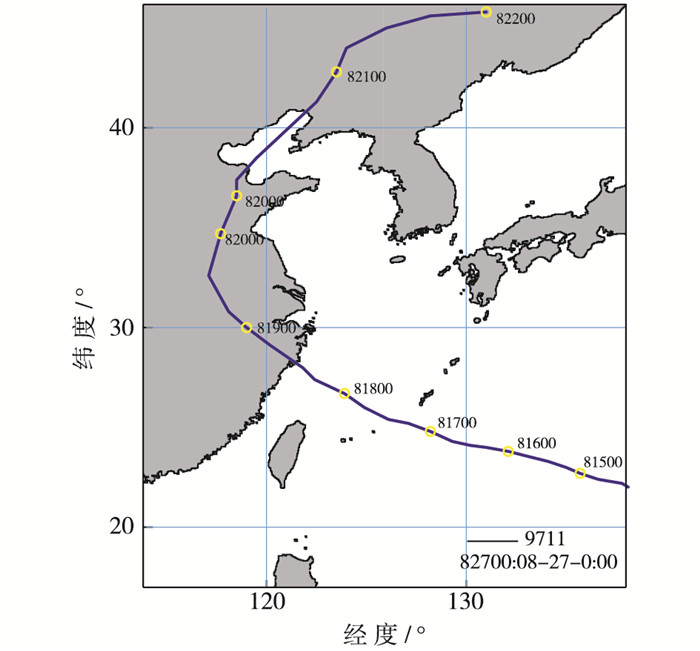
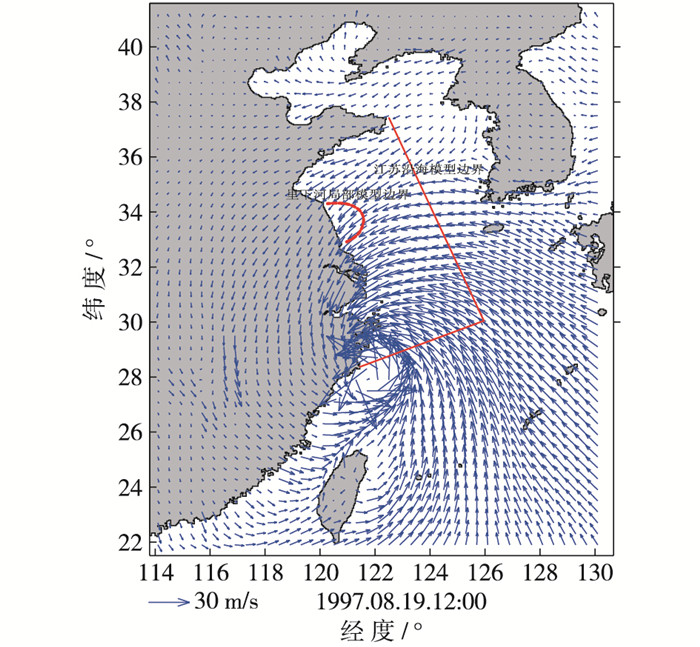
台风风场采用Holland模式[8-9],背景风场采用日本气象厅第二代全球气候再分析数据JAR-55。“9711”台风路径见图 3,台风登陆时风场见图 4。
|
图 3 “9711”台风路径 Figure 3 Trace of "9711" typhoon |
|
图 4 台风登陆时风场 Figure 4 Wind fields during of typhoon landfall |
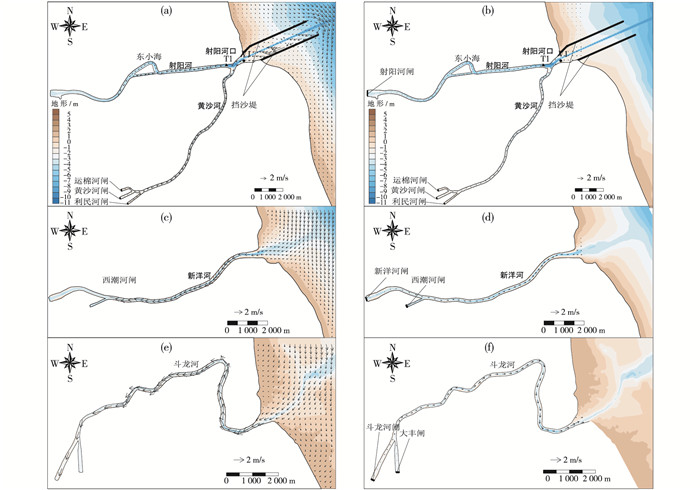
利用2006年8月射阳河口口内实测潮位和流速对局部模型进行验证,验证结果见图 5(T1和V1位置见图 6)。从验证结果可以看出,数学模型计算结果与实测结果比较一致,表明模型边界条件和参数设置合理。图 6为局部模型模拟的涨落潮流场(验证期间,射阳河口拦沙堤未建;为与目前现状一致,流场图为拦沙堤建成后工况)。由图可见,口外涨潮流沿河道上溯,由口门向口内流速大体呈先增后减趋势,在闸门处涨潮流速逐渐减小趋于0;落潮流速规律类似,但量值较小。

|
图 5 里下河局部模型潮位和流速验证(2006-08-09T16:00/2006-08-10T23:00) Figure 5 Tidal level and velocity verification of Lixiahe local model (2006-08-09T16:00/2006-08-10T23:00) |
|
图 6 里下河涨、落潮流场(a, c, e为涨潮;b, d, f为落潮) Figure 6 Flow fields of flood tide (a, c, e, ) and ebb tide (b, d, f) at Lixiahe |
由于局部模型范围内缺少站点风暴潮实测资料,给出江苏沿海风暴潮模型的验证情况。图 7为连云港站风暴潮水位和增水实测过程与计算过程比较,可以看出数学模型计算结果与实测结果吻合较好。

|
图 7 江苏沿海风暴潮数学模型验证 Figure 7 Storm surge verification of Jiangsu coastal model |
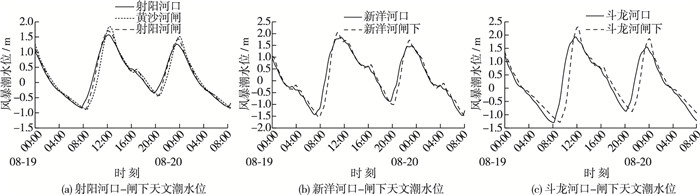
为更好地对比闸下风暴潮变化,首先计算了潮汐水位变化,计算潮汐边界条件为“9711”台风风暴增水期间的预报天文大潮(1997-08-19T00:00/1997-08-20T08:00),结果见图 8和表 2。计算结果显示:①在实例潮型下,各入海河流挡潮闸下高潮位均有所抬升,幅度为0.14~0.28 m;低潮位基本呈降低趋势,幅度约0.10 m;潮差均有所增加,幅度为9%~15%。②高潮位抬升幅度和潮差增加由北向南呈逐渐增加趋势,黄沙河闸下高潮位和潮差抬升幅度明显大于射阳河。③相对河口而言,闸下低潮时滞后60~70 min,高潮时则滞后10~20 min,因此,闸下水位涨潮历时比河口缩短50 min左右,而落潮历时则延长50 min左右。
|
图 8 河口-闸下天文潮过程比较 Figure 8 Comparisons between tidal level hydrographs during astronomical tide along mouth and downstream of tide sluice |
| 表 2 闸下潮汐变化 Table 2 Tidal level variations in downstream of tide sluice |
潮波由河道上溯过程中主要受到底摩擦、浅水变形、潮波反射等作用,其中底摩擦使得潮波振幅减小,高潮位降低,低潮位升高;而地形通过浅水项使得高潮时提前、低潮时滞后,即涨潮历时缩短,落潮历时延长,潮波不对称性加强。边界反射(闸门)使得潮波呈驻波性质,潮差增加,流速与潮位相位发生变化[10]。因此,闸下潮波的变化反映了浅水非线性效应、底摩擦、河口变形以及边界反射等相互作用的结果[11-12],即与河道地形、河槽宽度、河道形态、闸门位置等有关。本例中闸下河段长度分别为射阳河16.2 m,黄沙河13.9 m,新洋河11.5 m,斗龙河13.2 m;闸下河段宽度射阳河220 m,黄沙河120 m,新洋河170 m,斗龙河130 m;闸下河段平均底高程射阳河-3.7 m,黄沙河-2.4 m,新洋河-2.1 m,斗龙河-2.0 m。黄沙河、斗龙河宽度较窄,水深地形较浅,闸下潮汐水位变化相对显著。
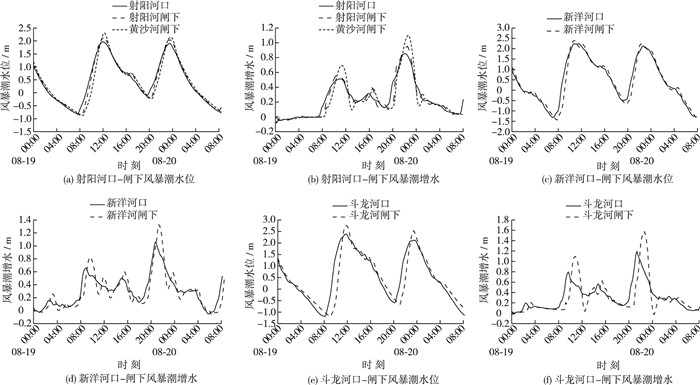
2.2 闸下风暴潮特征图 9为风暴潮水位和增水过程,表 3为里下河四港闸下与河口风暴潮水位特征值比较。可以看出:①闸下风暴潮的变化与潮汐变化特征几乎一致,但幅度有所增加。其中,闸下高潮位抬升幅度为0.15~0.37 m,最大增水增幅12%~32%。②不同河口之间高潮位和增水抬升幅度分布规律与潮汐变化一致。由北向南呈增加趋势。由于河道较窄、河底地形较浅,黄沙河闸下高潮位和增水抬升幅度相对较大。③闸下风暴潮水位同样存在潮时滞后、涨落潮历时不等的特征。滞后时间与潮汐过程基本一致。
|
图 9 闸下风暴潮过程比较 Figure 9 Comparisons between storm surge hydrographs along mouth and downstream of tide sluice |
| 表 3 闸下风暴潮变化 Table 3 Storm surge variations in downstream of tide sluice |
对比闸下风暴潮与潮汐变化可以看出,闸下风暴潮变化趋势与潮汐特征几乎完全一致,亦即闸下风暴潮高潮位和最大增水同样呈抬升趋势,而抬升幅度比潮汐水位和潮差更为明显。这说明作用于潮波变形的浅水非线性效应、底摩擦、河口变形以及边界反射等因素同样作用于风暴潮波在河道内的传播过程;且各因素综合作用使得闸下风暴潮变化趋势更为突出。
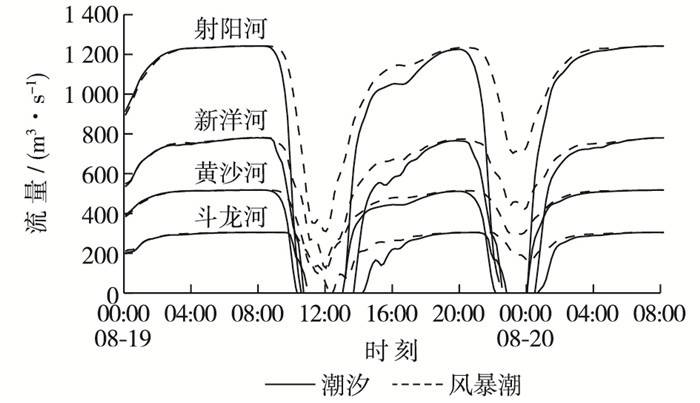
3 风暴潮对闸下排水影响以“9711”台风风暴潮为例,分析外海风暴潮对射阳河、新洋河和斗龙河闸下河道排水的影响。计算时,考虑到闸顶高程,设定闸上游水头为1.8 m,相当于闸门完全开启时的下沿。模拟了外海在天文潮和风暴潮作用下的排水过程,见图 10。可以看出,在天文潮条件下,设定闸上排洪条件时,河口闸均可排水。在1997-08-19T00:00/1997-08-20T08:00共32 h内,射阳河闸、黄沙河闸(包括运棉河闸和利民河闸)、新洋河闸和斗龙河闸排水总流量分别为89.4×106, 37.4×106, 54.5×106和21.8×106 m3。计算结果显示,“9711”风暴潮条件下,相同时间内,射阳河闸、黄沙河闸(包括运棉河闸和利民河闸)、新洋河闸和斗龙河闸排水量分别为71.6×106,30.1×106,42.0×106和16.7×106 m3;减少比例分别为19.9%,19.5%,23.0%和23.3%,即下降20%~25%。
|
图 10 潮汐、风暴潮条件下闸下排洪流量过程 Figure 10 Hydrographs of flood discharge from tide sluice under conditions of tide with storm surge |
以江苏里下河地区为例,通过平面二维数学模型模拟了里下河主要入海河流闸下潮汐水位和风暴潮水位过程,分析了闸下水位相比河口水位过程的变化特征,得出以下结论:
(1) 相对河口而言,由于受到底摩擦、浅水变形、潮波反射等相互作用影响,闸下潮汐水位存在明显变化:高潮位抬升,低潮位下降,潮差增加;涨潮历时缩短,落潮历时延长。潮汐水位变化幅度与河道地形、河槽宽度、河道形态、闸门位置等有关。
(2) 闸下风暴潮变化趋势与潮汐特征几乎完全一致,闸下风暴潮高潮位和最大增水同样存在抬升趋势,且抬升幅度相比潮汐水位和潮差更为显著。闸下河段风暴潮波受到浅水非线性效应、底摩擦、河口变形以及边界反射等因素作用更为突出。
(3) 风暴潮过程对于闸下排水具有显著影响。在与闸门顶高程一致的上游水位条件下,相比天文潮过程,计算实例中的风暴潮过程可影响闸门过流流量的20%~25%。
| [1] |
王向明, 张新周, 窦希萍, 等. 建闸河口闸下潮波变形数值模拟研究[J]. 水运工程, 2012(9): 18-23, 29. ( WANG Xiangming, ZHANG Xinzhou, DOU Xiping, et al. Numerical simulation of tidal wave deformation downstream sluice in estuary[J]. Port & Waterway Engineering, 2012(9): 18-23, 29. (in Chinese)) |
| [2] |
李明亮, 汪亚平, 朱国贤, 等. 中小型建闸河口的闸下水体悬沙输运过程:以新洋港河口为例[J]. 海洋通报, 2013, 32(6): 657-667. ( LI Mingliang, WANG Yaping, ZHU Guoxian, et al. Suspended sediment transport in small and medium estuaries with the sluice gate: a case study of the Xinyanggang Estuary, China[J]. Marine Science Bulletin, 2013, 32(6): 657-667. DOI:10.11840/j.issn.1001-6392.2013.06.008 (in Chinese)) |
| [3] |
张金善, 黄建维, 罗肇森, 等. 我国建闸河口闸下淤积问题及其对策[C]//中国海洋学会, 中国海洋湖沼学会海岸河口分会. 第九届全国河口海岸学术研讨会论文集(摘要), 2006. (ZHANG Jinshan, HUANG Jianwei, LUO Zhaosen, et al. Sediment siltation downstream tidal barriers and it's countermeasures in China[C]//Chinese Marine Institute, Chinese Institute of Oceanology and limnology in Coastal and Estuarine Branch. Proceedings of the Ninth National Symposium on Estuarine and Coastal Research (abstract), 2006. (in Chinese)) http://cpfd.cnki.com.cn/Article/CPFDTOTAL-EGVE200601002024.htm
|
| [4] |
徐雪松, 窦希萍, 陈星, 等. 建闸河口闸下淤积问题研究综述[J]. 水运工程, 2012(1): 116-121. ( XU Xuesong, DOU Xiping, CHEN Xin, et al. Overview of siltation downstream estuarine floodgates[J]. Port & Waterway Engineering, 2012(1): 116-121. (in Chinese)) |
| [5] |
LONGUET-HIGGINS M S, STEWART R W. Radiation stresses in water waves; a physical discussion, with applications[C]//Deep Sea Research and Oceanographic Abstracts, Elsevier, 1964, 11(4): 529-562. http://www.sciencedirect.com/science/article/pii/0011747164900014
|
| [6] |
章卫胜, 张金善, 林瑞栋, 等. 中国近海潮汐变化对外海海平面上升的响应[J]. 水科学进展, 2013, 24(2): 243-250. ( ZHANG Weisheng, ZHANG Jinshan, LIN Ruidong, et al. Tidal response of sea level rise in marginal seas near China[J]. Advances in Water Science, 2013, 24(2): 243-250. (in Chinese)) |
| [7] |
BLAIN C A, LINZELL R S, CHU P, et al. Validation Test Report for the ADvanced CIRCulation Model (ADCIRC) v45. 11[R]NRL/MR/7320-10-9205. Washington, DC: Naval Research Laboratory, 2010.
|
| [8] |
HOLLAND G J. An analytic model of the wind and pressure profiles in hurricanes[J]. Monthly Weather Review, 1980, 108(8): 1212-1218. DOI:10.1175/1520-0493(1980)108<1212:AAMOTW>2.0.CO;2 |
| [9] |
HOLLAND G J, BELANGER J I, FRITZ A. A revised model for radial profiles of hurricane winds[J]. Monthly Weather Review, 2010, 138(12): 4393-4401. DOI:10.1175/2010MWR3317.1 |
| [10] |
陈宗镛, 路季平. 一维水域潮波运动非线性和底摩擦效应的探讨[J]. 黄渤海海洋, 1988, 6(1): 1-6. ( CHEN Zongyong, LU Jiping. A study of nonlinear frictional effects on tidal propagation of one-dimensional water regions[J]. Journal of Oceanography of Huanghai & Bohai Seas, 1988, 6(1): 1-6. (in Chinese)) |
| [11] |
钱力强, 杜勇, 俞光耀. 一维水域潮波运动的变浅效应[J]. 海洋与湖沼, 1995, 26(增刊1): 32-39. ( QIAN Liqiang, DU Yong, YU Guangyao. On the shallow effect of the tidal in one-dimensional region[J]. Oceanologia Et Limnologia Sinica Supplement, 1995, 26(Suppl1): 32-39. (in Chinese)) |
| [12] |
杜勇, 陈宗镛, 叶安乐. 一种变截面河口中非线潮波的的研究[J]. 海洋学报, 1989, 11(6): 669-681. ( DU Yong, CHEN Zongyong, YE Anle. A study of nonlinear tidal wave in estuary with variable cross-section[J]. Acta Oceanologica Sinica, 1989, 11(6): 669-681. (in Chinese)) |
2. Water Resources Department of Jiangsu Province, Nanjing 210029, China
 2018
2018 
