2. 河海大学港口海岸与近海工程学院, 江苏 南京 210098;
3. 大连理工大学海岸与近海工程国家重点实验室, 辽宁 大连 116024
桩基础作为土木工程中最常用的基础结构形式,因其能较好地适应各种地质条件及荷载情况,且具有承载力高、沉降小等优点,被广泛应用于各类土木工程结构中[1-2]。在桩基础研究与设计中大多只考虑其竖向静荷载承载能力,而随着近岸与海洋资源的开发,在深水环境条件下,开敞式港口码头、海上采油平台等工程结构除承受静荷载外,在极端波浪、风以及地震等环境荷载作用下,结构还承受较大的水平动力荷载[3-7]。尤其在地震荷载作用下,饱和地基中超孔隙水压力的上升能显著加速地基承载力的下降,直至液化临界状态后完全丧失承载力,造成结构物失稳破坏[8-10]。在过去数十年发生的主要地震中,如日本的Niigata地震,Loma Prieta地震,Kobe地震等,由地基液化所导致的港口建筑、桥梁以及各类海洋平台结构的破坏案例均有所报道[11-12]。因此,研究地基液化产生机理,确保地基拥有足够的承载能力已成为结构抗震设计中的重要课题。
考虑到超孔隙水压的上升作为土体骨架与孔隙水耦合作用的结果[8],因此准确模拟土体在循环荷载作用下的非线性响应成为解决地基液化问题的必要前提。在土的弹塑性模型发展史上,基于临界状态理论[13]发展而来的剑桥模型是第1个基于试验且能够准确描述正常固结黏性土力学特性的经典土力学本构模型[14],并被广泛应用于土木与岩土工程实践中[15],但由于剑桥模型参数均基于正常固结重塑土三轴试验得到,因此严格意义上只适用于正常固结重塑土。然而在地震荷载或其他动力循环加载作用下,土体经历弹性卸载后即进入超固结状态。作为土体应力历史的反映,其对当前土体的力学特性有着不可忽略的影响[15]。为研究超固结土的力学特性,Nakai[16]与Asaoka[17]等学者通过引入下负荷面(subloading surface)概念,在剑桥模型基础上通过考虑超固结因素的影响提出了下负荷面剑桥模型,为研究循环交变荷载作用下的超固结演化规律以及在超固结状态影响下的土体力学特征提出了一个可行的理论框架[18]。
鉴于饱和地基地震液化的巨大影响以及土体循环加载下的复杂非线性特性,本文分别通过排水以及非排水循环加载试验对超固结土体强度以及超固结状态的发展规律进行了详细分析。并在此基础上,通过引入下负荷面剑桥模型本构关系,建立了饱和地基环境条件下的桩-土耦合体系在地震作用下的三维非线性动力有限元数值模型,通过数值模拟研究了饱和地基条件下桩柱结构的地震动力响应特性,对超固结因素的影响作用进行了详细对比分析。
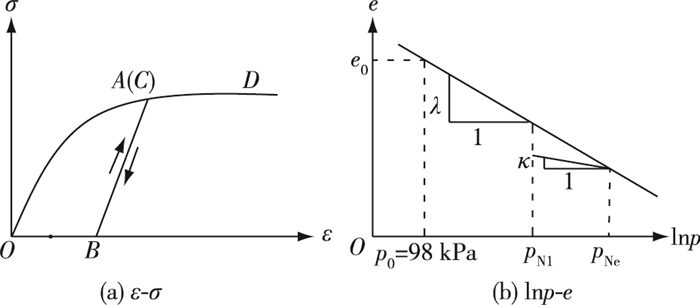
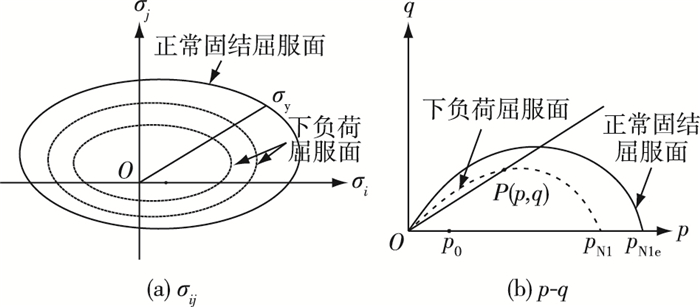
1 超固结下负荷面剑桥模型在剑桥模型以及其他经典土力学弹塑性理论中,在土的卸载及再加载过程中,其应力应变关系被假定为弹性关系(图 1(a)),而实际上即使在再加载过程中也会产生塑性应变。同时考虑到正常固结土一旦卸载,即变成超固结状态(图 1(b))。在经典弹塑性理论中,只存在一个屈服面,即正常固结屈服面(图 2(a)),若某一点应力状态处在此屈服面内(超固结状态),则假定其为弹性,这与实际试验观测现象不符。为解决这个问题很多学者提出了不同的模型。其中下负荷面模型的物理意义最为明确[14],可用状态变量的概念精确定义塑性势,且假定下负荷屈服面经过现有应力点并和正常屈服面几何相似,而且随应力变化而变化,因此也不需要判定应力状态是否到达屈服面,简化判定标准。
|
图 1 经典剑桥弹塑性理论加载过程曲线 Figure 1 Load curve of soil of classic Cam-clay model |
|
图 2 应力状态与下负荷面屈服面的关系 Figure 2 Stress condition and subloading yielding surface of soil |
尽管基于重塑黏土三轴试验发展而来的剑桥模型的应用范围存在局限性,未能考虑超固结因素的影响,但仍然成为现代诸多弹塑性理论模型的基础。剑桥模型采用塑性体应变硬化规律,以塑性体积应变εVp为硬化参数,且假定塑性变形符合相关联流动法则,其屈服函数为[14]:
| $ f = f\left( {p, q, \varepsilon _{\rm{V}}^{\rm{p}}} \right) = {C_{\rm{p}}}\ln \frac{p}{{{p_0}}} + {D^*}\eta-\varepsilon _{\rm{V}}^{\rm{p}} = 0 $ | (1) |
式中:εVp为硬化参数;CP=(λ-κ)/(1+e0),e0为参考大气压p0(98 kPa)下的孔隙比(图 1),λ=0.434Cc,κ=0.434Cs,Cc和Cs分别为土体的压缩系数与膨胀系数;D*=CP/M*;M*为临界状态下的剪切应力比;p和q为平均有效应力和剪应力,η=q/p为剪切应力比。
对图 2(b)中处于超固结状态的应力点P(p, q),由于下负荷剑桥模型假设下负荷屈服面与正常固结屈服面几何相似,则通过P点的下负荷屈服面fs可表示为:
| $ {f_{\rm{s}}} = {C_{\rm{p}}}\ln \frac{p}{{{p_{{\rm{N1}}}}}} + {D^*}\frac{q}{p} = 0 $ | (2) |
式中:pN1为下负荷屈服面与p轴的交点,而pN1e则为正常固结屈服面与p轴的交点。
根据应力关系,下负荷屈服面fs可写为:
| $ {f_{\rm{s}}} = {C_{\rm{p}}}\left[{\ln \frac{p}{{{p_0}}}-\left( {\ln \frac{{{p_{{\rm{N1e}}}}}}{{{p_0}}}-\ln \frac{{{p_{{\rm{N1e}}}}}}{{{p_{{\rm{N1}}}}}}} \right)} \right] + {D^*}\frac{q}{p} = 0 $ | (3) |
通过超固结状态变量
| $ {f_{\rm{s}}} = \ln \frac{p}{{{p_0}}} + \frac{1}{{{M^*}}}\frac{q}{p}-\frac{1}{{{C_{\rm{p}}}}}\varepsilon _{\rm{V}}^{\rm{p}}-\ln R = 0 $ | (4) |
将方程变换到一般应力空间:
| $ {f_{\rm{s}}} = \ln \frac{{{\sigma _m}}}{{\sigma _{m0}^*}} + \frac{{\sqrt 3 }}{{{M^*}}}\frac{{\sqrt {{J_2}} }}{{{\sigma _m}}}-\frac{1}{{{C_{\rm{p}}}}}\varepsilon _{\rm{V}}^{\rm{p}}-\ln R = 0 $ | (5) |
式中:σm=σii/3,J2=sijsij/2,sij=σij-σm。对于超固结状态参数R的发展,根据Nakai和Asaoka等[16-17]的建议,取dR=Udεdp,其中dεdp为塑性剪切应变增量,
通过协调方程联合Hooke定律可得到下负荷面剑桥模型的弹塑性本构关系(其中Eijkl为弹性刚度张量,εkl,εkle和εklp分别为总应变张量、弹性应变张量和塑性应变张量):
| $ \begin{array}{l} {\rm{d}}{\sigma _{ij}} = {E_{ijkl}}{\rm{d}}\varepsilon _{kl}^{\rm{e}} = {E_{ijkl}}\left( {{\rm{d}}{\varepsilon _{kl}}-{\rm{d}}\varepsilon _{kl}^{\rm{p}}} \right)\\ \;\;\;\;\;\;\; = {E_{ijkl}}{\rm{d}}{\varepsilon _{kl}}-{E_{ijkl}}\Lambda \frac{{\partial f}}{{\partial {\sigma _{kl}}}} \end{array} $ | (6) |
| $ \mathit{\Lambda = }\frac{{\frac{{\partial f}}{{\partial {\sigma _{ij}}}}{E_{ijkl}}{\rm{d}}{\varepsilon _{kl}}}}{{{h^{\rm{p}}} + \frac{{\partial f}}{{\partial {\sigma _{ij}}}}{E_{ijkl}}\frac{{\partial f}}{{\partial {\sigma _{kl}}}}}}, {h^{\rm{p}}} = \frac{1}{{{C_{\rm{p}}}}}\left\{ {\frac{{\partial f}}{{\partial {\sigma _{mm}}}}-\frac{{{m_{\rm{R}}}\ln R}}{R}\frac{1}{{{\sigma _m}}}} \right\} $ |
通过模型本构关系的建立,得到以下加载准则:①加载时,|dεijp|>0,Λ>0及
为验证模型的可靠性以及研究超固结因素对土体力学和液化特性的影响,本文在下负荷面剑桥模型下,分别通过排水与非排水循环加载试验进行了数值模拟试验研究。试验土以藤森黏土为例[17],主要参数λ=0.09,κ=0.02,e0=0.88,M*=1.36,mR=2.1,泊松比ν=0.2,γ=20.4 kN/m3。
2.1 单调加载下数值模拟验证图 3为平均主应力一定条件下(98 kPa)的三轴压缩试验结果[17]与下负荷面剑桥模型预测值对比结果,其中OCR为超固结比。

|
图 3 模型预测与三轴试验结果对比 Figure 3 Comparison of model predicted results and triaxial tests results |
由图 3可见,下负荷面剑桥模型很好地模拟了超固结土的应力软化及剪胀现象。4种不同超固结状态土的屈服强度计算值分别达到1.36,1.53,1.72和1.92(图 3(a))。相较于重塑土,超固结土的屈服强度得到显著提高,屈服强度与超固结比间表现出明显的正相关性。而在加载屈服过程中,随着加载过程中超固结比的衰减(图 3c),土体的加载响应开始软化,并在完全屈服后均趋于同一应力水平。图 3(b)给出了加载屈服过程中土体的体积压缩过程曲线。从图中压缩曲线的发展规律可以看出,在加载初始阶段,所有土体在剪切应力作用下均经历了1个明显的体积压缩过程。其中正常固结土的孔隙比压缩量达到3.5%,而对于超固结土,随着加载过程中超固结状态的不断衰减(图 3(c)),使得孔隙比朝着增长的方向发展(Δe),并在屈服后表现出明显的剪胀特性,尤其在高超固结比条件下,其剪胀现象表现得更为显著(Δe=1.19%, 2.41%, 3.21%)。
2.2 循环加载数值模拟试验通过单调加载试验对比研究可以看出,通过考虑超固结因素的影响,下负荷面剑桥模型对超固结土在单调加载下的屈服过程和剪胀现象能够做出准确描述。而在循环交变荷载作用下,考虑到土体的屈服过程同时伴随着超固结状态的演化发展,尤其在饱和非排水加载条件下,伴随着超孔隙水压的升高与有效应力的减小能加速土体的软化进程,直至达到液化状态后完全失去承载能力。为进一步研究土体的循环加载响应与液化特性,以及初始超固结比的影响作用,本文分别在排水和非排水条件下对3种超固结比条件下(OCR=1,2,4)土体的循环交变荷载作用下的应力应变响应关系、可压缩性以及相应的孔压、超固结比状态的发展规律进行了数值对比试验研究。试验加载幅值σ1-σ3为100 kPa,应变加载步长Δεd=0.002,总试验步数为2 000步。
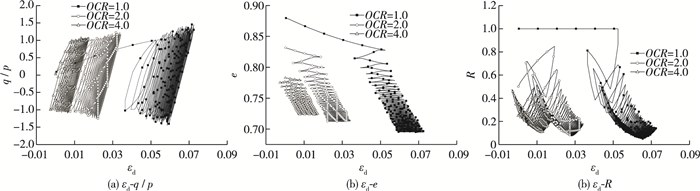
图 4即为三轴排水条件下的循环加载试验结果,从图中试验结果的对比可以看出,相较于正常固结土,随着超固结比的提高,超固结土在循环加载过程中表现出更小的塑性变形与非线性特性,且在循环加载过程中伴随着超固结状态逐渐达到稳定状态后(图 4(c)),其应力应变关系也随之达到稳定状态。同样从土体压缩过程曲线(图 4(b))也可以看出,在正常固结土中,孔隙比压缩量达到0.18,而在超固结土下其压缩量分别为0.12和0.06,相较于正常固结土,超固结土表现出更低的可压缩性。
|
图 4 排水三轴压缩试验 Figure 4 Drained triaxial tests under cyclic loading |
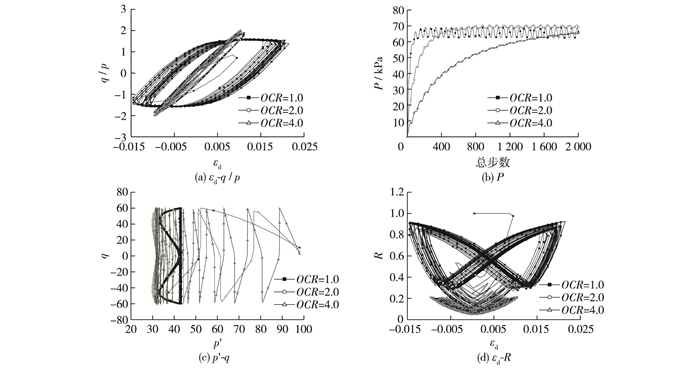
图 5为非排水条件下循环加载试验结果,与排水试验条件下所有土体均被压缩至最终稳定状态不同,在非排水条件下随着超孔隙水压的上升,尤其在正常固结条件下,土体应力应变响应曲线表现为更大的回滞圈。图 5(b)给出了循环加载过程中超孔隙水压的发展过程曲线,从图中对比可见,由于正常固结土的高可压缩性,使得土体加载应力转移至孔隙水上,导致土体有效应力随之减小(图 5(c)),并最终影响土体应力应变关系响应曲线。同样从超固结比的演化过程曲线(图 5(d))的对比也可以看出,由于非排水条件加载下土体无法压缩至最终稳定状态,在循环加载过程中相应的超固结比演化在循环荷载作用下表现出更加明显的波动过程。
|
图 5 非排水三轴压缩试验 Figure 5 Undrained tests under cyclic loading |
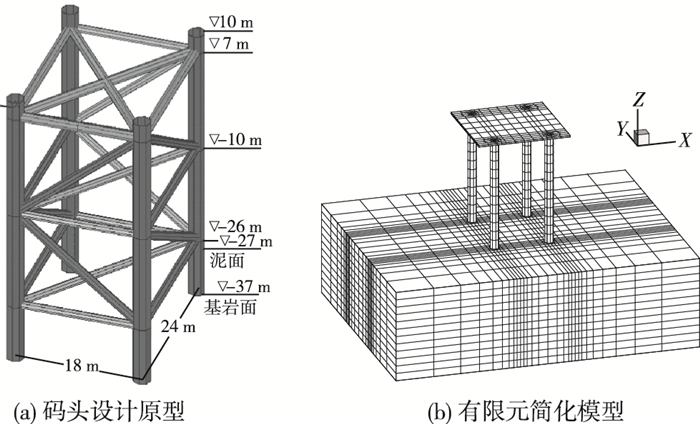
通过对超固结因素的研究可以看出,土体的超固结状态能够显著影响土体的力学特性,尤其在循环非排水条件下考虑土体超固结因素后能显著影响土体的超孔隙水压上升速率、加速土体的软化过程。为进一步研究超固结因素在饱和地基下桩柱结构地震响应中的影响作用,在ADINA81有限元程序的基础上开发了剑桥模型和下负荷面剑桥模型,并以一简化四桩柱码头结构为例对结构的非线性地震响应进行了模拟研究。码头计算原型为离岸深水港岩基浅埋轻型的四桩钢管结构码头(6(a))[19],在本文的数值模型中,为简化计算模型,仅保留了钢管桩码头的主桩结构,并对上部结构的荷载进行了简化。其中码头结构模型上部结构距离泥面35 m,桩柱在地面以下部分长20 m,结构自重2 000 kN,流体的影响以附加水质量的形式简化考虑。钢管桩桩径为2.8 m,壁厚32 mm,弹性模量210 GPa,材料密度7 800 kg/m3,桩柱结构成18 m×24 m布置(图 6)。地基土以藤森黏土为例,计算域取100 m×40 m×30 m,在截断面上采取黏弹性边界以模拟半无限空间中地震波的运动。输入地震波采用Loma波[9]进行模拟计算(图 7)。为更好对比研究结构的非线性地震响应,本文数值模拟中将Loma波放大至0.2g作为入射波进行对比计算。
|
图 6 桩柱码头原型与简化有限元模型网格 Figure 6 Prototype of the pipe pier and simplified finite element mesh model |
|
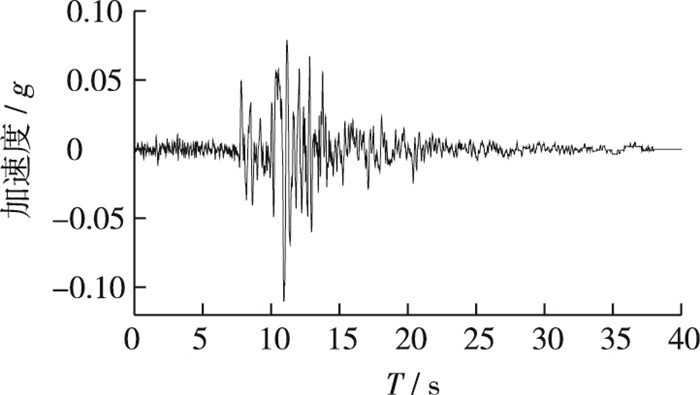
图 7 输入地震波加速度时程曲线 Figure 7 Time-history of input seismic acceleration |
以下负荷面剑桥模型计算结果为例给出了震后地基中超孔隙水压比的分布云图(见图 8(a))。从图中超孔隙水压分布可以看出,受桩土间动力耦合作用的影响,桩侧附近土体的超孔隙水压显著高于远场地基,且随着深度的增加,桩柱与自由场间运动差异减小,相应的超孔隙水压比差异随之降低。为进一步对比研究不同模型下超孔隙水压分布规律,图 8(b)给出了桩柱附近以及地基远场在深度方向上的超孔隙水压比分布。从图中曲线对比可以看出,超孔隙水压比在地表处达到最大值,尤其在近场处受桩土动力耦合作用的影响,地表附近已达到液化状态。而随着地基深度的加深,超孔隙水压比呈现出明显的指数衰减趋势。在5 m深处,在剑桥模型和下负荷面剑桥模型下近场超孔隙水压比分别达到0.91和0.60,随着深度的继续增加,在20 m深度位置相应的超孔隙水压比分别降低为0.36和0.30。而通过不同模型地基下超孔隙水压曲线对比可以看出,在考虑超固结影响因素后,在地震作用下地基表现出了更好的抗液化能力。

|
图 8 地基中超孔隙水压比分布 Figure 8 Distribution of excess pore water pressure ratios |
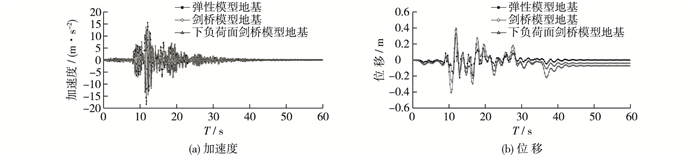
图 9给出了不同模型下结构顶点动力响应对比,为更好对比研究结构的非线性地震响应,本文同时在理想弹性地基(E=3(1-2ν)(1+e0)p/κ)假设下对结构的地震响应进行了数值模拟,并将其计算结果作为参考背景对结构的非线性响应进行了对比分析。从图中对比结果可以看出,结构的地震动力响应峰值加速度分别达到18.36, 12.91和14.34 m/s2,相应的位移峰值为0.29, 0.41和0.34 m。相较于理想弹性地基,在考虑土体非线性因素后,随着地基土的屈服,结构模型的整体刚度降低,尤其在剑桥模型下表现得更加明显,结构加速度响应更小,而由于地基承载力的下降,结构在地震作用下表现出更高的位移响应,并在震后表现出更显著的塑性位移(0,0.07和0.04 m)。
|
图 9 桩柱结构顶点动力响应 Figure 9 Dynamic response of structure's top node |
为进一步研究地震作用下桩柱结构的受力情况,通过桩柱截面上的应力积分,图 10给出了桩柱的弯矩包络图。同样为方便对比桩柱结构中的弯矩,图中弯矩值均以弹性地基计算结果作为参照基准以相对值给出。从图中弯矩曲线可以看出,在整个桩身中弯矩包络曲线存在两个明显的峰值,且在泥面附近处达到最大值。相较于理想弹性地基模型,剑桥模型与下负荷面剑桥模型地基下最大弯矩值分别达到1.36和1.10。通过本文结构算例的地震动力响应与受力结果对比可以看出,在考虑超固结因素后,下负荷面剑桥模型模拟计算结果介于弹性模型与剑桥模型之间,相较于剑桥模型,地基表现出了更好的抗液化与承载能力。

|
图 10 桩柱弯矩包络图 Figure 10 Bending moment envelope of pile |
通过考虑超固结因素的影响,本文在下负荷面剑桥模型下对超固结土力学强度、可压缩性,以及非排水循环加载试验下超孔隙水压的发展规律进行了数值模拟研究。并在ADINA81程序基础上通过剑桥模型和下负荷面剑桥模型本构关系模块的开发,对饱和地基条件下桩柱结构的地震响应进行了有限元数值模拟研究,得到以下主要结论:
(1) 通过对超固结状态演化过程的模拟,下负荷面剑桥模型能够准确模拟出超固结土单调加载屈服过程中的应力软化以及体积剪胀等特性。相较于正常固结土,随着超固结比的增大,土体的屈服强度也相应得到显著提高,但在土体最终屈服退化为正常固结状态后,超固结土与正常固结土的屈服应力趋于一致。
(2) 在排水循环荷载作用下,随着土体被压缩至其稳定密实状态的同时达到更高超固结状态,且相较于正常固结土,由于超固结土较小的初始孔隙比,在循环加载下表现出更低的可压缩性; 在非排水循环加载下,相较于正常固结土,超固结土能够更好地维持其初始稳定状态,表现出更好的受力与抗液化特性。
(3) 在饱和地基桩柱结构地震模拟数值算例中,受桩土间动力耦合作用的影响,桩柱结构近场地基的超孔隙水压要显著高于远场地基。同时通过不同土体本构模型下模拟计算结果的对比可以看出:下负荷面剑桥模型下得到的地震响应模拟结果介于理想弹性模型与剑桥模型之间; 相较于剑桥模型,在考虑超固结因素后,由于超固结土更好的抗液化以及力学特性,随着相应模型下地基承载能力的提高,结构的地震响应与受力情况均得到明显改善。
| [1] |
KAUSEL E. Early history of soil-structure interaction[J]. Soil Dynamics and Earthquake Engineering, 2010, 30(9): 822-832. DOI:10.1016/j.soildyn.2009.11.001 |
| [2] |
ASHOUR M, ARDALAN H. Piles in fully liquefied soils with lateral spread[J]. Computers and Geotechnics, 2011, 38(6): 821-833. DOI:10.1016/j.compgeo.2011.05.001 |
| [3] |
刘祚秋, 周翠英, 温少荣, 等. 桩-土-承台结构在波浪力作用下的力学效应分析[J]. 岩土力学, 2005, 26(7): 1109-1112. ( LIU Zuoqiu, ZHOU Cuiying, WEN Shaorong, et al. Stress state analysis of the structure of piles, soil and base slab under wave loads[J]. Rock and Soil Mechanics, 2005, 26(7): 1109-1112. (in Chinese)) |
| [4] |
尚守平, 余俊, 王海东, 等. 饱和土中桩水平振动分析[J]. 岩土工程学报, 2007, 29(11): 1696-1702. ( SHANG Shouping, YU Jun, WANG Haidong, et al. Horizontal vibration of piles in saturated soil[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(11): 1696-1702. DOI:10.3321/j.issn:1000-4548.2007.11.017 (in Chinese)) |
| [5] |
MEMARPOUR M M, KIMIAEI M, SHAYANFAR M, et al. Cyclic lateral response of pile foundations in offshore platforms[J]. Computers and Geotechnics, 2012, 42(3): 180-192. |
| [6] |
DAMGAARD M, BAYAT M, ANDERSEN L V, et al. Assessment of the dynamic behaviour of saturated soil subjected to cyclic loading from offshore monopile wind turbine foundations[J]. Computers and Geotechnics, 2014, 61(3): 116-126. |
| [7] |
EI-DIN M N, KIM J. Sensitivity analysis of pile-founded fixed steel jacket platforms subjected to seismic loads[J]. Ocean Engineering, 2014, 85(15): 1-11. |
| [8] |
唐亮, 凌贤长, 徐鹏举, 等. 土体液化动力分析数值模型[J]. 哈尔滨工业大学学报, 2010, 42(4): 521-524. ( TANG Liang, LING Xianzhang, XU Pengju, et al. Numerical model for dynamic analysis of soil liquefaction[J]. Journal of Harbin Institute of Technology, 2010, 42(4): 521-524. DOI:10.11918/j.issn.0367-6234.2010.04.004 (in Chinese)) |
| [9] |
王睿, 张建民, 张嘎. 液化地基侧向流动引起的桩基础破坏分析[J]. 岩土力学, 2011, 32(增刊1): 501-506. ( WANG Rui, ZHANG Jianmin, ZHANG Ga. Analysis of failure of piled foundation due to lateral spreading in liquefied soils[J]. Rock and Soil Mechanics, 2011, 32(Suppl1): 501-506. (in Chinese)) |
| [10] |
HEIDER Y, AVCI O, MARKERT B, et al. The dynamic response of fluid-saturated porous materials with application to seismically induced soil liquefaction[J]. Soil Dynamics and Earthquake Engineering, 2014, 63: 120-137. DOI:10.1016/j.soildyn.2014.03.017 |
| [11] |
刘惠珊. 桩基抗震设计探讨—日本阪神大地震的启示[J]. 工程抗震与加固改造, 2000, 22(3): 27-32. ( LIU Huishan. A discussion on seismic design of pile foundation[J]. Earthquake Resistant Engineering and Retrofitting, 2000, 22(3): 27-32. (in Chinese)) |
| [12] |
FUKUSUMI T, OZAKI H, KOBAC M. Influence of the ground profile on the reduction of earthquake motion at the filled man-made islands in the Kobe harbor during the 1995 Hyogoken Nambu earthquake[J]. Journal of Soil Dynamics and Earthquake Engineering, 2002, 22(9): 893-899. |
| [13] |
ROSCOE K H, SCHOFIELD A, WROTH C P. On the yielding of soils[J]. Geotechnique, 1958, 8(1): 22-53. DOI:10.1680/geot.1958.8.1.22 |
| [14] |
张锋. 计算土力学[M]. 北京: 人民交通出版社, 2007: 173-174. ( ZHANG Feng. Computational soil mechanics[M]. Beijing: China Communication Press, 2007: 173-174. (in Chinese))
|
| [15] |
姚仰平, 张丙印, 朱俊高. 土的基本特性、本构关系及数值模拟研究综述[J]. 土木工程学报, 2012, 45(3): 127-150. ( YAO Yangping, ZHANG Bingyin, ZHU Jungao. Behaviors, constitutive models and numerical simulation of soils[J]. China Civil Engineering Journal, 2012, 45(3): 127-150. (in Chinese)) |
| [16] |
NAKAI T, HINOKIO M. A simple elastoplastic model for normally and over consolidated soils with unified material parameters[J]. Soils and Foundations, 2004, 44(2): 53-70. DOI:10.3208/sandf.44.2_53 |
| [17] |
ASAOKA A, NAKANO M, NODA T. A super/subloading yield surface approach to compaction/liquefaction of sand and secondary consolidation of clay[C]//Geomechanics II-Testing, Modeling and Simulation, Proceedings of the Second GI-JGS workshop, Osaka: ASCE Geotechnical Special Publication, 2006: 201-218. http://cedb.asce.org/CEDBsearch/record.jsp?dockey=153965
|
| [18] |
CHOO H, BURNS S E. Effect of overconsolidation ratio on dynamic properties of binary mixtures of silica particles[J]. Soil Dynamics and Earthquake Engineering, 2014, 60: 44-50. DOI:10.1016/j.soildyn.2014.01.015 |
| [19] |
张卫平, 孙昭晨, 梁书秀. 离岸深水港轻型码头在波浪作用下动力响应研究[J]. 水运工程, 2014(3): 74-79. ( ZHANG Weiping, SUN Zhaochen, LIANG Shuxiu. Dynamic response research of offshore deepwater light pier under wave action[J]. Port and Waterway Engineering, 2014(3): 74-79. (in Chinese)) |
2. College of Harbor, Coastal and Offshore Engineering, Hohai University, Nanjing 210098, China;
3. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China
 2018
2018 
