来自河流上游的淡水和来自河口外的盐水相遇,因密度差异,形成淡水在表盐水在底的水体分层现象。在径流淡水持续供给和周期性潮汐动力的作用下,盐淡水水体层化混合发生周期性的变化,改变了河口垂向水流结构及河口余流场分布,进而影响河口物质和能量的输运过程。
纵观国内外各大河口,均存在着盐淡水混合的现象[1-5],因径流量和潮动力强度的差异,水体的分层混合现象有所区别。美国的James河口潮动力弱,水体分层现象显著[6];中国的瓯江河口潮动力强,径流量较小,盐淡水混合比较充分,水体分层现象相对弱[7]。Simpson等[1]在研究Liverpool湾时总结提出了影响河口盐淡水分层混合的三大主要控制因子:河口环流、潮汐应变和潮汐紊动,随后应用在英国Rhine河口[2],美国York河口[3]等的层化混合机制研究中。时钟等[8]也将Simpson的潮汐应变理论应用于长江口水体层化混合机制的研究中,认为在长江口水体层化混合过程中,潮汐应变具有一定的作用。Scully等[9]总结得出对于大多数河口,落潮期潮汐应变的作用将引起更强的水体分层。Trowbridge等[10]利用测量的Hudson河口下游的流速、密度和压力梯度数据,研究了河口水体紊动、垂向流速的结构及河口动量平衡的问题。Li等[11]采用大涡模拟的方法研究了河口横向密度梯度对水体混合的影响,并重现了水体周期性分层的现象。
磨刀门是珠江河口的八大口门之一,也是西江的主要出海口,在潮汐和径流的共同作用下,垂向各层不同密度水体在此产生周期性的分层混合现象,该现象将直接影响磨刀门的水动力条件,进而影响其泥沙、污染物等物质的输运,为此根据磨刀门水道枯季大潮水文测量资料,开展盐致层化混合现象研究,确定层化混合程度的变化及其动力机制。
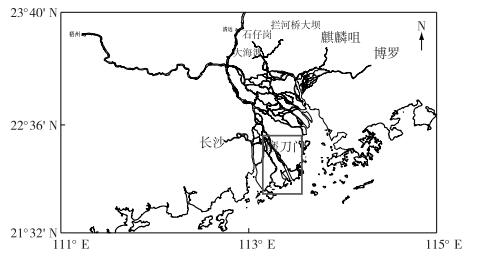
1 研究区域珠江河口由八大口门组成,包括东四口门和西四口门,磨刀门属于其西四口门之一,位于西江下游,具体位置见图 1。磨刀门水道长约45 km,水深变化范围为5~13 m。总体上宽度小于3 km,并且在接近口门处自西向东分成三叉:河洲水道,磨刀门水道和洪湾水道。口门处向海一侧有拦门沙存在,使得水深最浅达3 m。
|
图 1 研究区域地理位置 Figure 1 Location of research area |
珠江河口的八大口门中磨刀门为径流最强的口门,年平均径流量为883.9亿m3,占西江和北江总流量的31.85%。流量有明显的季节性,多年平均流量为7 400 m3/s,枯季为3 420 m3/s,洪季为11 400 m3/s。磨刀门也是珠江河口八大口门中潮差最小的口门,口门处潮差约1.1 m。
本次研究区域为磨刀门水道竹排沙水位站以下的盐水入侵影响范围河段,约28 km。
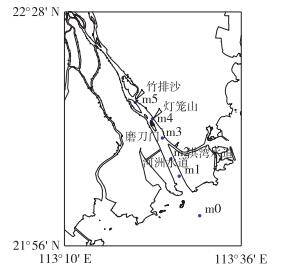
2 实测资料采用磨刀门水道水文测量时间为2009-01-12T14:00/2009-01-13T18:00(共28 h)的资料,测量期间上游西江马口站径流量为3 560~3 200 m3/s,处于枯季大潮期。研究区域共布设6个测点,包括m0, m1, m2,m3,m4,m5,位置分布如图 2所示,测点m0位于磨刀门外,m1,m2测点位于洪湾水道下游,m3,m4,m5测点位于洪湾水道上游。测量内容包括垂线水深、流速、流向以及盐度,除m0采用垂向3点法测量,其余测点的后三项数据均按6点法测得,包括水面,0.2h,0.4h,0.6h,0.8h和水底(h为水深),所有数据均为每小时观测1次。
|
图 2 研究区域地形及测点位置 Figure 2 Topography of research area and locations of gauge stations |
层化混合特征指标是反应河口垂向各层不同密度水体层化混合程度的依据,不同学者根据各自的分析需要,提出了评价层化混合程度的特征指标,其中常用的有整体Richardson数、梯度Richardson数、层化势能函数φ等。
(1) 整体Richardson数 整体Richardson数(Rio)反映垂向各层不同密度水体层化混合的平均状态,可表示为[12]:
| $ Rio = - \frac{{g\Delta \rho H}}{{\bar \rho {{\left( {\Delta U} \right)}^2}}} $ | (1) |
式中:g为重力加速度; Δρ和ΔU为水体表底层的密度差和流速差,
整体Richardson数可以用来判断垂向各层不同密度水体层化或混合的整体状态,当Rio < 1时,处于混合状态,反之处于层化状态。
(2) 梯度Richardson数 梯度Richardson数(Ri)描述了垂向浮力效应与垂向紊动效应的相对关系,表达式如下[13]:
| $ Ri = - \frac{g}{\rho }\frac{{\partial \rho }}{{\partial z}}{\left( {\frac{{\partial u}}{{\partial z}}} \right)^{ - 2}} $ | (2) |
式中:z为垂向距离; u为各层流速。
梯度Richardson数可以用于判断垂向各层的层化混合状态,具有鉴别密度跃层的功能。Nepf和Geyer研究Hudson河时[14],指出层化混合状态临界值为Ri=0.4,即当Ri>0.4时,层化作用较大,水体趋于稳定; 当Ri < 0.4时,混合强烈,紊动导致水体垂向密度趋于一致。此临界值视不同河口而定,可以肯定的是梯度Richardson数越大,其层化越强,反之混合越强。
(3) 势能函数φ 势能函数φ由Simpson提出,认为河口垂向各层不同密度水体层化混合是势能和动能转化的结果,该势能为某一位置瞬时密度分层状态发生完全混合所需要的能量,可表示为:
| $ \varphi = \frac{g}{H}\int\limits_0^H {\left( {\bar \rho - \rho } \right)z{\rm{d}}z} $ | (3) |
式中:φ为水体势能函数。
可以看出,水体密度分层越发育,势能函数φ越大。
层化混合各指标中,水体密度利用Millero等的海水状态方程求得:
| $ \rho = {\rho _0} + AS + B{S^{3/2}} + C{S^2} $ | (4) |
式中:ρ0,A,B,C皆为水体温度的函数; S为水体盐度; T为水温,在此取恒定常温(10 ℃,下为恒定)。
| $ \begin{array}{l} {\rho _0} = 999.842\;594 + 6.793\;952 \times {10^{ - 2}}T - 9.095 \times {10^{ - 3}}{T^2} + 1.001\;685 \times {10^{ - 4}}{T^3} \\- 1.120\;083 \times {10^{ - 6}}{T^4} + 6.536\;332 \times {10^{ - 9}}{T^5} \end{array} $ |
| $ A = 8.244\;93 \times {10^{ - 1}} - 4.0899 \times {10^{ - 3}}T + 7.6438 \times {10^{ - 5}}{T^2} - 8.2467 \times {10^{ - 7}}{T^3} \\+ 5.3875 \times {10^{ - 9}}{T^4} $ |
| $ B = - 5.724\;66 \times {10^{ - 3}} + 1.022\;7 \times {10^{ - 4}}T - 1.6545 \times {10^{ - 6}}{T^2},C = 4.831\;4 \times {10^{ - 4}} $ |
层化混合机制分析采用Simpson势能理论,即导致垂向各层不同密度水体层化混合的动力因子包括:河口环流、潮汐应变、潮汐紊动以及风搅动,其中河口环流促进水体层化; 潮汐应变涨潮时促进水体混合,落潮时促进水体层化; 潮汐紊动由水流与地形摩擦导致,削弱层化; 风搅动由风和水体表面摩擦导致,促进水体混合。
(1) 河口环流 河流淡水入海引起河口水平盐度梯度,水平盐度梯度驱使表层低浓度水体向海,底部高浓度水体向陆的剪切环流。假定水平密度梯度与水深无关,则有:
| $ \frac{{\partial \rho }}{{\partial t}} = - u\frac{{\partial \rho }}{{\partial x}};\frac{{\partial \bar \rho }}{{\partial t}} = - \bar u\frac{{\partial \bar \rho }}{{\partial x}} $ | (5) |
剪切环流对势能函数φ的贡献可推导如下:
| $ \frac{{\partial \varphi }}{{\partial t}} = \frac{g}{H}\int\limits_0^H {\left( {\frac{{\partial \bar \rho }}{{\partial t}} - \frac{{\partial \rho }}{{\partial t}}} \right)z{\rm{d}}z} = \frac{g}{H}\frac{{\partial \rho }}{{\partial x}}\int\limits_0^H {\left( {u - \bar u} \right)z{\rm{d}}z} $ | (6) |
式中:
根据河口环流的稳态结构理论[16],在假定径流为定常流,压力梯度与摩擦力相平衡且底部边界无滑移的条件下,水体垂向流速分布可用下式表示:
| $ u\left( \xi \right) = \frac{{g{H^3}}}{{48{N_{\rm{Z}}}\rho }}\frac{{\partial \rho }}{{\partial x}}\left( {1 - 9{\xi ^2} - 8{\xi ^3}} \right) $ | (7) |
式中:ξ为水深相对坐标,ξ=z/H,NZ=2.5×103|
将式(7)代入式(6),得到由河口环流导致的水体势能变化率:
| $ {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{\rm{E}}} = \frac{{{g^2}{H^4}}}{{320{N_{\rm{Z}}}\rho }}{\left( {\frac{{\partial \rho }}{{\partial x}}} \right)^2} $ | (8) |
(2) 潮汐应变 Bowden和Fairbairn[17]采用的水体垂向流速分布公式为:
| $ u\left( \xi \right) = \bar u\left( {a - b{\xi ^2}} \right) $ | (9) |
式中:a,b为经验常数,a=1.15,b=0.425。
代入式(6),得到由潮汐应变引起的水体势能变化率为:
| $ {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{\rm{STR}}}} = 0.031gH\bar u\frac{{\partial \rho }}{{\partial x}} $ | (10) |
(3) 潮汐紊动 潮汐紊动是由水体与底床摩擦以及水体各层之间的剪切流所导致的,并由底层向上传递,破坏水体分层,加剧混合。潮汐紊动引起的水体势能变化率为[18]:
| $ {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{\rm{STI}}}} = \frac{{ - e{C_{\rm{D}}}\rho {{\left| {\bar u} \right|}^3}}}{H} $ | (11) |
式中:e为潮汐混合系数,e=3.8×10-3; CD为底部拖曳力系数,CD=2.5×10-3。
(4) 风搅动 风搅动对混合的促进作用主要影响水体表面,对于风速较小且风区为河道型水域的地区,可忽略该项作用[2]。结合磨刀门水道特点,在此忽略风应力对水体紊动的影响。
结合以上影响水体层化混合的因素,得到河口区域的水体混合所需能量的变化率计算式为:
| $ \frac{{\partial \varphi }}{{\partial t}} = {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{\rm{E}}} + {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{\rm{STR}}}} + {\left( {\frac{{\partial \varphi }}{{\partial t}}} \right)_{{\rm{STI}}}} = \frac{{{g^2}{H^4}}}{{320{N_{\rm{Z}}}\rho }}{\left( {\frac{{\partial \rho }}{{\partial x}}} \right)^2} + 0.031gH\bar u\frac{{\partial \rho }}{{\partial x}} + \frac{{ - e{C_{\rm{D}}}\rho {{\left| {\bar u} \right|}^3}}}{H} $ | (12) |
考虑到水体分层主要发生在磨刀门水道,因此选取测点m1,m2,m3,m5进行分析。
4.1 水动力变化特征图 3为磨刀门各测点的潮位、流速逐时变化过程,表 1为各测点涨、落潮过程特征数据。可以看出各测点的潮位和流速均发生半日周期性变化,根据对灯笼山水位站的潮位调和分析得出全日分潮对半日分潮比值,(HK1+HO1)/HM2=1.6,属于不规则半日潮; 潮流调和分析结果显示,测点m1和m2全日分潮流速对半日分潮流速比值(WK1+WO1)/WM2=0.89和0.82,属于不规则半日潮流。从河口至上游,潮差沿程减小,涨、落潮沿水深平均流速逐渐减小,说明潮动力逐渐减弱。各测点落潮历时要大于涨潮历时,并且从m1至m5点涨潮历时逐渐减小,落潮历时逐渐增加,存在明显的不对称性现象。表层流速过程和底层流速过程存在明显的相位差,m2和m3点该现象最显著,该两点在涨憩左右时刻,底层尚表现为涨潮流时,表层已发生落潮,这势必对依赖于淡水和盐水的层化混合现象产生重要影响。
| 表 1 磨刀门水道各测点涨落潮过程特征值 Table 1 Characteristic values during flood-ebb cycle in the Modaomen waterway |

|
图 3 磨刀门水道各测点流速剖面随时间变化(单位:m/s) Figure 3 Time series of velocity profile in the Modaomen waterway (unit: m/s) |
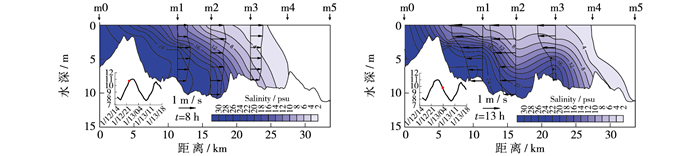
图 4为涨、落潮垂向流速剖面,可以看出在涨潮阶段,垂向流速梯度相对较小,最大流速并非出现在水面,而是出现在盐跃层界面以下,m1和m2测点该现象特别明显,在盐跃层界面上的流速要小于界面下; 落潮阶段盐跃层位置的垂向流速梯度大大增强,最大流速出现在盐跃层以上低盐度区,高盐度区流速不大,m1和m3测点该现象特别明显。因此,无论是涨潮期还是落潮期,存在高流速梯度的盐跃层均是上下水体之间发生动量交换和物质交换的位置。
|
图 4 涨、落潮期间磨刀门水道垂向流速剖面和盐度等值线 Figure 4 Velocity profile and salinity contour along the Modaomen waterway at the flood and ebb time |
图 5为磨刀门各测点盐度逐时变化过程,可以看出涨落潮期间均存在着表层盐度低,底层盐度高的分层现象,形成盐水楔,所不同的是其形状和位置在涨落潮时期所有差异。各测点盐度过程呈现与潮动力相应的周期性变化规律,盐度峰值出现在涨憩后1~2 h。Hansen和Rattary[19]提出无量纲参数

|
图 5 磨刀门水道各测点盐度剖面随时间变化(psu) Figure 5 Time series of salinity profiles in Modaomen waterway |
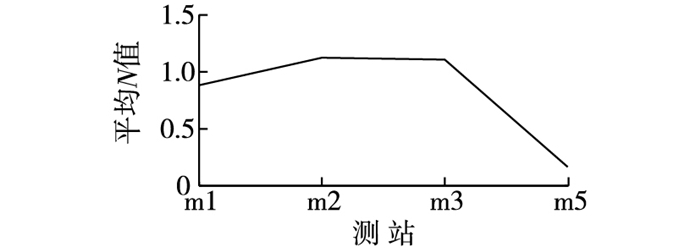
如图 6所示,从河口向上游,各测点平均N值先增后减。根据判别标准,当N≥1时,河口类型为高度分层型; 当1>N≥0.01时,河口类型为部分混合型; N<0.01时,河口类型为强混合型,磨刀门河口平均N值为0.69,因此磨刀门河口属于部分混合型河口。
|
图 6 各测点盐度分层系数 Figure 6 Salinity stratification N along the Modaomen waterway |
平面上,沿着河道方向各测点盐度从河口至上游总体呈现逐渐减小的趋势,但是在落潮过程中,出现了上游m3的盐度大于下游m2的盐度的情况,如图 7所示,发生此现象的原因是磨刀门水道、洪湾水道及河洲水道的盐水上溯存在相位差,在磨刀门水道落潮初期,来自洪湾水道和河洲水道的盐水依然还在注入磨刀门水道,导致上游m3的盐度大于下游m2,且高盐度区位于底部。
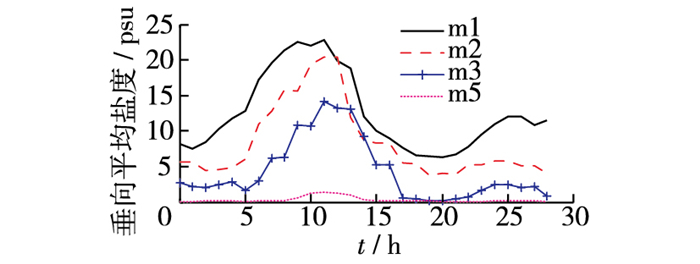
|
图 7 各测点平均盐度变化 Figure 7 Averaged salinity variation |
如前所述,磨刀门河口属于部分混合型河口,为此进一步从整体Richardson数、梯度Richardson数和势能函数φ3个层化混合指标来分析磨刀门水道水体层化混合时空变化特征。
4.3.1 整体Richardson数图 8为磨刀门水道各测点整体Richardson数和沿水深平均流速随时间变化图,为了方便,图中整体Richardson数做了对数处理,因此lgRio=0可作为判断水体层化与混合的临界值,正值处于层化状态,负值处于混合状态。

|
图 8 磨刀门水道各测点整体Richardson数随时间变化 Figure 8 Time series of overall Richardson number for gauge stations in the Modaomen waterway |
由图 8可知,各测点整体Richardson数随着潮动力发生周期性变化。lgRio正峰值均出现在涨憩时刻附近,此时水体层化最强。此后随着落潮流速的增强,lgRio值逐渐减小,混合增强,负极值一般位于落急之后1~3 h。随着落潮流速的减小,尽管lgRio还是负值,尚处于混合状态,但层化作用不断增强,落憩左右至混合层化临界值,即lgRio=0。再次进入涨潮阶段,垂向水体已经由混合状态进入分层状态,并且分层逐渐增强,至涨憩时刻附近,lgRio再次达到正峰值。测点m1,m2,m3层化混合状态维持时间比例约为2:1,大部分时间水体处在层化状态; 测点m5层化混合状态维持时间比例约为1:5,绝大部分时间水体处在混合状态。与图 5中的盐度比较,前3个测点的盐度相对较大,层化现象明显且稳定; 上游m5点水体受径流控制作用,盐度很小,层化现象很不明显。
4.3.2 梯度Richardson数图 9为磨刀门水道各测点梯度Richardson数等值线图。

|
图 9 磨刀门水道各测点垂向梯度Richardson数随时间变化 |
为方便表述,采用lgRi数绘制,以临界值0.4或1推算,层化混合临界值取对数后分别为:-0.398和0。在磨刀门水道,可采用大值作为判别层化混合的临界值。
若以lgRi=0等值线为标准,从m1到m5,小于0的部分面积先减小后增大,说明水体的层化先增强后减弱,最大值发生在测点m2和m3,说明最强层化区域位于洪湾水道、河洲水道和磨刀门水道连接区段。靠近m1测点,垂向紊动作用强,在落憩时刻垂向表现出最大范围的混合,越往上游由于径流引起的势能增强,潮动力减弱,层化效应也就越强。m5水体含盐度很低,所以垂向的分层现象不是很明显,水体仅在涨憩至落急之前,出现明显分层,其余时间均为混合状态。利用梯度Richardson数的时空变化,还可以看出磨刀门水道盐跃层的时空分布特征。从m1点至m5点,可以看出最大lgRi中心在不断地下沉,这也体现了磨刀门盐水楔的时空变化,盐跃层存在的时间发生在涨潮-涨憩-落潮时期。根据图 3、图 4和图 5,盐跃层位置处的垂向流速梯度和盐度均发生较大变化,对照图 9,可将lgRi=0作为盐跃层位置的判定标准。
4.3.3 势能函数φ势能函数φ既能体现垂向密度分层发育程度,也能反映盐度梯度势能的输移。图 10为磨刀门水道各测点相关参数随时间变化过程。
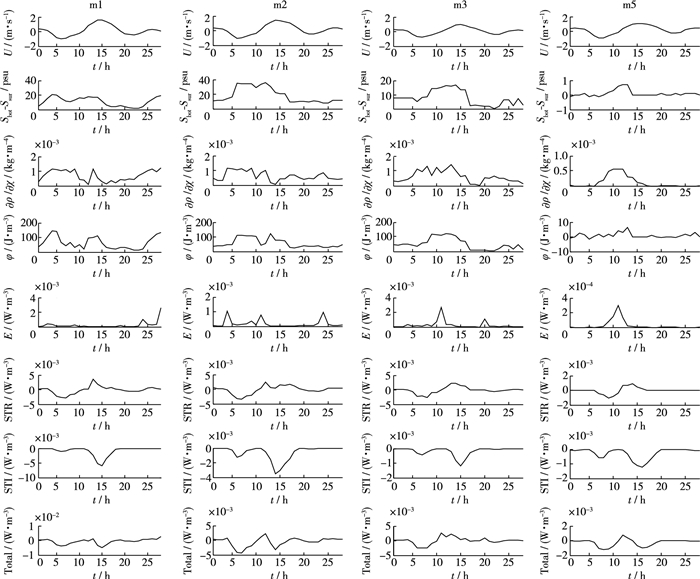
|
图 10 磨刀门水道各测点相关参数随时间变化 Figure 10 Time series of related parameters for gauge stations in the Modaomen waterway |
从图 10可见,势能函数φ值的沿程变化特征:m1至m5势能函数φ值逐渐减小; 各测点势能函数峰值出现时间有所差异,m1点出现了2次峰值,第1次出现在落憩和涨急之间,第2次出现在涨憩和落急之间,m2点势能函数峰值第1次出现在涨急时刻,第2次出现在落急时刻,m3,m5点势能函数峰值出现时刻逐渐依次向后推移。以上特征说明盐致密度势能在潮汐作用下由河口向上游传输能量,势能能量逐渐消耗减少,各位置势能传输存在相位差,对比流速和盐度过程,其能量的传输与盐度传输更趋于一致。
4.4 势能变化机制分析计算导致磨刀门水道测点势能函数变化的各动力因子:河口环流、潮汐应变和潮汐紊动及三项之和,结果如图 10所示。
4.4.1 河口环流引起势能变化率大潮期间,各测点的河口环流引起势能变化率均大于等于0,说明河口环流不断促进水体层化。河口环流引起的势能变化率在涨憩、落憩转流时刻附近出现极值。盐水在潮动力作用下向上游输送,在涨潮期,盐水上溯导致水平密度梯度增大,如图 10第3行所示,而涨憩、落憩转流时刻,水体垂向平均流速小,导致转流时刻河口环流引起的势能变化率出现极值,因涨憩时刻水深更大,涨憩时刻的河口环流引起势能变化率极值也要比落憩时刻的极值更大,此现象在测点m3, m5表现更为明显。对比图 9、图 10,河口环流引起势能变化率极值出现时期正好也是层化混合特征指标的峰值时期,河口环流促使水体表层淡水向海输运,底层盐水向陆输运,导致河口垂向水体层化加强。表 2为磨刀门水道各测点势能变化率特征值统计,可以看出各测点的河口环流引起势能变化率的平均值和极值,均为从河口向上游先增大后减少,至m3测点达到最大,至m5测点达到最小,原因是上游测点水体盐度很小,水平密度梯度小导致。
| 表 2 磨刀门水道各测点势能变化率特征值 Table 2 Characteristic values of potential energy rate in the Modaomen waterway |
如图 10,潮汐应变引起势能变化率的变化过程与流速有着良好的对应关系。涨潮流流速向陆,势能变化率为负值,潮汐应变促使水体混合; 落潮时径流和潮汐的运动方向均向河口外,表层流速大,底层流速小产生相位差,潮汐应变引起势能变化率为正值,促进水体的层化。潮汐应变引起势能变化率正、负极值基本出现在落急、涨急时刻。潮汐应变引起势能变化率所表现出的随涨落潮周期变化的特性,将在水体垂向引起周期性层化。如表 2所示,不同测点潮汐应变引起的层化势能变化率均大于河口环流引起的层化势能变化率,但两者量级相当。潮汐应变引起势能层化量值从河口向上游,各测点数值总体也是先增大后减小,说明潮汐应变引起层化作用在m2和m3点效果最为显著; 潮汐应变引起的垂向水体混合作用,也是在m2点最为显著。总结认为,潮汐应变促使水体层化混合周期性变化在盐淡水主要混合区最为强烈。
4.4.3 潮汐紊动引起势能变化率如图 10所示,潮汐紊动引起势能变化率均为负值,潮汐紊动不断促进各层水体交换混合。潮汐紊动引起势能变化率极值出现在涨急、落急时刻,流速越大,与底床摩擦越强烈,进而紊动越剧烈,混合越强,其中落急时刻潮汐紊动引起势能变化率大于涨急时刻。如表 2所示,磨刀门水道从河口向上游,各测点潮汐紊动引起势能变化率总体逐渐减小,因潮汐紊动的能量主要取决于潮动力,因此分析认为上述原因是向上游沿程潮动力逐渐减弱所致。
4.4.4 讨论综合上述影响因子,决定各测点水体层化混合随着涨落潮周期性变化的是总势能变化率,即河口环流、潮汐应变和潮汐紊动三项之和。如图 10所示,磨刀门水道各测点的层化混合特征指标与总势能变化率的正负交替有着良好的对应关系。总势能变化率的最大值代表此时水体层化增长最大,基本在涨憩或涨憩后1~2 h,其具体出现时刻与河口环流和潮汐应变产生的层化效应哪项为主导有很大的关系; 总势能变化率的负极值位置与潮汐紊动引起势能变化率的极值有较好的对应关系,最小值的位置在涨急或落急时刻,但具体并不确定,与河口环流、潮汐应变和潮汐紊动三者各自引起的势能变化率的相对大小有关。同时,在磨刀门水道落潮初期,来自洪湾水道和河洲水道的盐水依然还在注入磨刀门水道,增大磨刀门水道水体的密度梯度,增强潮汐应变作用。对比m1~m5各测点河口环流、潮汐应变和潮汐紊动引起势能变化率层化部分和混合部分量值可知落潮阶段,潮汐应变的层化作用要大于河口环流的层化作用; 涨潮阶段,潮汐应变的混合作用要大于潮汐紊动的混合作用,因此认为磨刀门水道水体层化混合周期性变化的控制动力因子是潮汐应变。
5 结语依据珠江磨刀门水道2009年枯季大潮的实测数据,分析了磨刀门水道水动力基本特征,探讨了磨刀门水道枯季大潮期间垂向各层不同密度水体层化混合周期性变化的机制,总结如下:
(1) 磨刀门水道枯季大潮期间,潮动力呈现不规则半日特性; 盐跃层处垂向流速梯度变化明显; 表底层流速过程存在相位差,出现底涨表落的现象。
(2) 盐度呈现周期性变化,盐水楔存在明显; 落潮初期洪湾水道和河洲水道对磨刀门水道的盐水注入加剧水体层化; 磨刀门河口盐度分层系数平均值为0.69,属部分混合型河口。
(3) 采用Simpson势能理论,分析得到河口环流、潮汐应变和潮汐紊动是水体层化混合周期性变化的影响因子; 河口环流加剧水体层化,潮汐紊动促进水体混合,潮汐应变在涨潮时促进混合,在落潮时促进层化,是引起垂向各层不同密度水体周期性层化混合现象的主控因子。
| [1] |
SIMPSON J H, BROWN J, MATTHEWS J, et al. Tidal straining, density currents, and stirring in the control of estuarine stratification[J]. Estuaries and Coasts, 1990, 13(2): 125-132. DOI:10.2307/1351581 |
| [2] |
SIMPSON J H, BURCHARD H, FISHER N R, et al. The semi-diurnal cycle of dissipation in a ROFI: model-measurement comparisons[J]. Continental Shelf Research, 2002, 22(11-13): 1615-1628. DOI:10.1016/S0278-4343(02)00025-0 |
| [3] |
SIMPSON J H, WILLIAMS E, BRASSEUR L H, et al. The impact of tidal straining on the cycle of turbulence in a partially stratified estuary[J]. Continental Shelf Research, 2005, 25(1): 51-64. DOI:10.1016/j.csr.2004.08.003 |
| [4] |
张重乐, 沈焕庭. 长江口咸淡水混合及其对悬沙的影响[J]. 华东师范大学学报(自然科学版), 1988(4): 83-88. ( ZHANG Chongle, SHEN Huanting. Mixing of salt-and fresh-water in the Changjiang estuary and its effects on suspended sediment[J]. Journal of East China Normal University(Natural Science), 1988(4): 83-88. (in Chinese)) |
| [5] |
WANG X H, WANG H. Tidal straining effect on the suspended sediment transport in the Huanghe(Yellow River) Estuary, China[J]. Ocean Dynamics, 2010, 60(5): 1273-1283. DOI:10.1007/s10236-010-0298-y |
| [6] |
SHEN J, LIN J. Modeling study of the influences of tide and stratification on age of water in the tidal James River[J]. Estuarine Coastal & Shelf Science, 2006, 68(1): 101-112. |
| [7] |
JIANG H Z, SHEN Y M, WANG S D. Numerical study on salinity stratification in the Oujiang River Estuary[J]. Journal of Hydrodynamics, 2009, 21(6): 835-842. DOI:10.1016/S1001-6058(08)60220-6 |
| [8] |
李霞, 胡国栋, 时钟, 等. 长江口南支南港的北槽枯季水体中混合、层化与潮汐应变[J]. 水运工程, 2013(9): 79-88, 94. ( LI Xia, HU Guodong, SHI Zhong, et al. Mixing, stratification and tidal straining in dry season within the north passage of the south branch/south channel of the Changjiang River estuary[J]. Port & Waterway Engineering, 2013(9): 79-88, 94. (in Chinese)) |
| [9] |
SCULLY M E, GEYER W R, LERCZAK J A. The influence of lateral advection on the residual estuarine circulation: A numerical modeling study of the Hudson River estuary[J]. Journal of Physical Oceanography, 2009, 39(1): 107-124. DOI:10.1175/2008JPO3952.1 |
| [10] |
TROWBRIDGE J H, GEYER W R, BOWEN M M, et al. Near-bottom turbulence measurements in a partially mixed estuary: Turbulent energy balance, velocity structure, and along-channel momentum balance[J]. Journal of Physical Oceanography, 1999, 29(12): 3056-3072. DOI:10.1175/1520-0485(1999)029<3056:NBTMIA>2.0.CO;2 |
| [11] |
LI M, TROWBRIDGE J H, GEYER W R. Asymmetric tidal mixing due to the horizontal density gradient[J]. Journal of Physical Oceanography, 2008, 38(2): 418-434. DOI:10.1175/2007JPO3372.1 |
| [12] |
BOWDEN K F. Turbulent mixing in estuaries[J]. Ocean Management, 1981, 6(2-3): 117-135. DOI:10.1016/0302-184X(81)90033-0 |
| [13] |
STACEY M T, RIPPETH T P, NASH J D. Turbulence and stratification in estuaries and coastal seas[J]. Treatise on Estuarine and Coastal Science, 2011, 9-35. |
| [14] |
NEPF H M, GEYER W R. Intratidal variations in stratification and mixing in the Hudson estuary[J]. Journal of Geophysical Research Atmospheres, 1996, 1011(C5): 12079-12086. |
| [15] |
MILLERO F J, POISSON A. International one-atmosphere equation of state of seawater[J]. Deep-sea Research, 1981, 28: 625-629. DOI:10.1016/0198-0149(81)90122-9 |
| [16] |
OFFICER C B. Physical oceanography of estuaries and associated coast waters[M]. New York: John Wiley and Sons, 1976.
|
| [17] |
BOWDEN K F, FAIRBAIRN L A. A determination of the frictional forces in a tidal current[J]. Proceedings of the Royal Society A, 1952, 214(1118): 371-392. DOI:10.1098/rspa.1952.0175 |
| [18] |
SIMPSON J H, BOWERS D G. Models of stratification and frontal movement in shelf seas[J]. Deep-Sea Research, 1981, 28(7): 727-738. DOI:10.1016/0198-0149(81)90132-1 |
| [19] |
HANSEN D V, RATTRAY J M. Gravitational circulation in straits and estuaries[J]. Journal of Marine Research, 1965, 23: 104-122. |
 2018
2018 