2. 大连理工大学 海岸与近海工程国家重点实验室, 辽宁 大连 116024;
3. 浙江大学 海洋学院, 浙江 杭州 310058
沿岸流作为近岸流的一种,人们很早就已经认识这一水动力现象[1-3],从波浪辐射应力的概念出发分析沿岸流,是对沿岸流研究的重要发展。该方法认为,波浪斜向入射,从深水区传到浅水区,因水深减小引起浅水变形,使得波高增大,最终发生破碎,而波浪破碎后通过破波带时,为平衡辐射应力梯度,将沿岸波动动量转化为时均沿岸流动从而产生了波生沿岸流。刘秋兴等[4]指出波浪辐射应力对于近岸风暴增减水起着十分重要的作用,郑金海等[5-6]总结了波浪辐射应力理论的应用和研究进展,并给出了波浪辐射应力张量的垂向变化。对于规则波作用下辐射应力的计算,Longuet-Higgins和Stewart[7]已经给出成熟的结果,对于不规则波作用下的辐射应力,李孟国等[8]给出了综合考虑多种变形因素的近岸多向不规则波传播数学模型,唐军等[9]考虑到入射波浪的随机性,采用JONSWAP[10]波浪谱对入射处单向不规则波浪要素进行离散,基于抛物型缓坡方程中的波浪势函数等参数计算波浪辐射应力[11],并对数值模拟结果进行了验证。相对于规则波,不规则波更能反映实际波浪的运动状况,本文通过将不规则波视为一系列规则波(微幅波)的叠加给出不规则波作用下辐射应力的计算方法,包含不规则波辐射应力的精确计算方法和近似计算方法,并对两种计算方法进行了分析比较,在此基础上进一步用试验结果[12]对不规则波辐射应力近似计算方法中的关键变量波能进行了验证。结果表明窄谱情况下,近似计算方法已有很好的精度,可节省大量的计算时间,从而提高计算效率。
1 不规则波辐射应力精确计算方法本节通过将不规则波视为一系列规则波(微幅波)的叠加来计算不规则波的辐射应力。首先考虑单向不规则波,其波面升高可表达为:
| $ \eta \left( {x,t} \right) = \sum\limits_{i = 1}^\infty {{A_i}\cos \left( {{k_i}x - {\omega _i}t + {\varepsilon _i}} \right)} = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^\infty {{A_i}\exp \left( {i{\theta _i}} \right)} } \right\} $ | (1) |
式中:θi=kix-ωit+εi;Ai为组成波的波幅,由波浪能量谱S(ω)确定;Re表示对复数取实部。
| $ {A_i} = \sqrt {2S\left( {{\omega _i}} \right)\Delta \omega } $ | (2) |
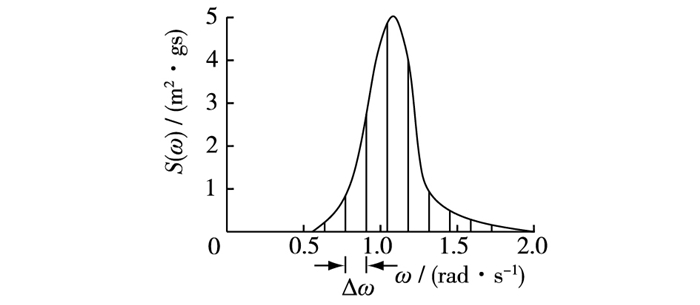
式中:ki和ωi分别为组成波的波数和频率;εi为随机相位(在0~2π间平均分布)。式(1)是将不规则波看作一系列规则波(微幅波)的叠加。各组成波的频率和波幅由将波能谱分割成宽为Δω的条形的中心频率和面积确定,见图 1。这里的分割是等间距的,Δω为常数。
|
图 1 波浪能量谱及其分割 Figure 1 Wave energy spectrum and its division |
因为控制体两个铅垂侧面上
| $ \rho \frac{\partial }{{\partial x}}\overline {\int_z^\eta {\tilde u\tilde w{\rm{d}}z} } - \overline {\rho {{\tilde w}^2}} = \bar p - \rho g\left( { - z + \bar \eta } \right) $ | (3) |
可得x和y方向的辐射应力为
| $ {S_{xx}} = \rho \int_{ - h}^0 {\left( {\overline {{{\tilde u}^2}} - \overline {{{\tilde w}^2}} } \right){\rm{d}}z} + \rho g\overline {{\eta ^2}} /2 + \rho \int_{ - h}^0 {\int_z^0 {\partial \overline {\tilde u\tilde w} /\partial x{\rm{d}}z{\rm{d}}z} } $ | (4) |
| $ {S_{yy}} = \rho \int_{ - h}^0 {\left( {\overline {{{\tilde v}^2}} - \overline {{{\tilde w}^2}} } \right){\rm{d}}z} + \rho g\overline {{\eta ^2}} /2 + \rho \int_{ - h}^0 {\int_z^0 {\partial \overline {\tilde u\tilde w} /\partial x{\rm{d}}z{\rm{d}}z} } $ | (5) |
式中:
由波浪水质点的速度势函数
| $ \mathit{\Phi }\left( {x,z,t} \right) = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^\infty {\frac{{{A_i}g}}{{i{\omega _i}}}\frac{{\cosh {k_i}\left( {z + h} \right)}}{{\cosh {k_i}h}}\exp \left( {i{\theta _i}} \right)} } \right\} $ | (6) |
可得
| $ \tilde u\left( {x,z,t} \right) = \frac{{\partial \mathit{\Phi }}}{{\partial x}} = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^\infty {\frac{{g{A_i}{k_i}}}{{{\omega _i}}}\frac{{\cosh {k_i}\left( {z + h} \right)}}{{\cosh {k_i}h}}\exp \left( {i{\theta _i}} \right)} } \right\} $ | (7) |
| $ \tilde w\left( {x,z,t} \right) = \frac{{\partial \mathit{\Phi }}}{{\partial x}} = {\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^\infty {\frac{{g{A_i}{k_i}}}{{i{\omega _i}}}\frac{{\sinh {k_i}\left( {z + h} \right)}}{{\cosh {k_i}h}}\exp \left( {i{\theta _i}} \right)} } \right\} $ | (8) |
由两复数β1和β2的运算公式(式中“*”表示复数共轭)
| $ {\mathop{\rm Re}\nolimits} \left\{ {{\beta _1}} \right\}{\mathop{\rm Re}\nolimits} \left\{ {{\beta _2}} \right\} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{\beta _1}{\beta _2}} \right\} + \frac{1}{2}\left\{ {{\beta _1}\beta _2^ * } \right\} $ | (9) |
可得
| $ \overline {{{\tilde u}^2}} - \overline {{{\tilde w}^2}} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{g^2}\sum\limits_{i = 1}^\infty {\sum\limits_{j = 1}^\infty {\left( {\frac{{{A_i}{k_i}}}{{{\omega _i}}}} \right)\left( {\frac{{{A_j}{k_j}}}{{{\omega _j}}}} \right)\exp \left( {i\left( {{\theta _i} - {\theta _j}} \right)} \right)} } \frac{{\cosh \left( {{k_i} - {k_j}} \right)\left( {z + h} \right)}}{{\cosh \left( {{k_i}h} \right)\cosh \left( {{k_j}h} \right)}}} \right\} $ | (10) |
| $ \frac{{\partial \overline {\tilde u\tilde w} }}{{\partial x}} = - \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {{g^2}\sum\limits_{i = 1}^\infty {\sum\limits_{j = 1}^\infty {\frac{{{A_j}{k_j}}}{{{\omega _j}}}\frac{{{A_i}{k_i}}}{{{\omega _i}}}\exp \left( {i\left( {{\theta _i} - {\theta _j}} \right)} \right)\left( {{k_i} - {k_j}} \right)} } \frac{{\sinh {k_j}\left( {z + h} \right)\cosh {k_i}\left( {z + h} \right)}}{{\cosh \left( {{k_j}h} \right)\cosh \left( {{k_i}h} \right)}}} \right\} $ | (11) |
| $ \overline {{\eta ^2}} = \frac{1}{2}{\mathop{\rm Re}\nolimits} \left\{ {\sum\limits_{i = 1}^\infty {\sum\limits_{j = 1}^\infty {{A_i}{A_j}\exp \left( {i\left( {{\theta _i} - {\theta _j}} \right)} \right)} } } \right\} $ | (12) |
将式(10)和(12)代入式(4)和(5)可得
| $ \begin{array}{*{20}{c}} {{S_{xx}} = \frac{1}{2}\rho g\sum\limits_{i = 1}^\infty {\left\{ {A_i^2\left( {2{n_i} - \frac{1}{2}} \right) + \sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^\infty {{A_i}{A_j}\left( {\frac{{{k_j}{\omega _i}/{\omega _j} - {k_i}{\omega _j}/{\omega _i}}}{{{k_i} - {k_j}}} + \frac{1}{2}} \right)\cos \left( {{\theta _i} - {\theta _j}} \right)} + } \right.} }\\ {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^\infty {\frac{{{A_i}{A_j}}}{{{{\bar c}_i}{{\bar c}_j}}}\left( {{\theta _i} - {\theta _j}} \right)\left[ {\frac{1}{{{k_i} + {k_j}}}\left( {{k_j} - {k_i}\tanh \left( {{k_i}h} \right)\tanh \left( {{k_j}h} \right)} \right)} \right.} - }\\ {\left. {\left. {\frac{{k_i^2 + k_j^2}}{{\left( {{k_i} + {k_j}} \right)h\left( {k_i^2 - k_j^2} \right)}}\left( {\frac{{2{k_i}{k_j}}}{{k_i^2 + k_j^2}}\tanh {k_i}h - \tanh {k_j}h} \right)} \right]} \right\}} \end{array} $ | (13) |
| $ \begin{array}{*{20}{c}} {{S_{yy}} = \frac{1}{2}\rho g\sum\limits_{i = 1}^\infty {\left\{ {A_i^2\left( {{n_i} - \frac{1}{2}} \right) + \sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^\infty {{A_i}{A_j}\left( {\frac{{k_j^2{\omega _i}/{\omega _j} - k_i^2{\omega _j}/{\omega _i}}}{{k_i^2 - k_j^2}} + \frac{1}{2}} \right)\cos \left( {{\theta _i} - {\theta _j}} \right)} + } \right.} }\\ {\sum\limits_{\begin{array}{*{20}{c}} {j = 1}\\ {j \ne i} \end{array}}^\infty {\frac{{{A_i}{A_j}}}{{{{\bar c}_i}{{\bar c}_j}}}\cos \left( {{\theta _i} - {\theta _j}} \right)\left[ {\frac{1}{{{k_i} + {k_j}}}\left( {{k_j} - {k_i}\tanh \left( {{k_i}h} \right)\tanh \left( {{k_j}h} \right)} \right)} \right.} - }\\ {\left. {\left. {\frac{{k_i^2 + k_j^2}}{{\left( {{k_i} + {k_j}} \right)h\left( {k_i^2 - k_j^2} \right)}}\left( {\frac{{2{k_i}{k_j}}}{{k_i^2 + k_j^2}}\tanh {k_i}h - \tanh {k_j}h} \right)} \right]} \right\}} \end{array} $ | (14) |
式中:
| $ {{\bar c}_i} = \frac{{{\omega _i}/{k_i}}}{{\sqrt {gh} }},{{\bar c}_j} = \frac{{{\omega _j}/{k_j}}}{{\sqrt {gh} }},{n_i} = \frac{1}{2}\left( {1 + \frac{{2{k_i}h}}{{\sinh 2{k_i}h}}} \right) $ |
对以α角度入射的行进波,可应用二维张量坐标变换得到相应的辐射应力张量,此时
| $ S = \left( {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \alpha } \end{array}} \right)\left( {\begin{array}{*{20}{c}} {{S_{xx}}}&0\\ 0&{{S_{yy}}} \end{array}} \right){\left( {\begin{array}{*{20}{c}} {\cos \alpha }&{ - \sin \alpha }\\ {\sin \alpha }&{\cos \alpha } \end{array}} \right)^{ - 1}} $ | (15) |
上面精确的计算方法可单独考虑不规则波的每一个组成波,但每一个时间步都要对各组成波进行累积求和,计算量较大。这里对其进行简化近似,以达到计算速度和精度都合适的结果。该方法是针对窄波能谱情况,即波谱S(ω)只在峰频ω附近才有较大数值。这样的波谱所对应波面具有明显波群特征。
由波浪能量谱S(ω)确定波面η(x, t)的表达式之后,可得波面时间历程的包络表达式为
| $ A\left( {x,t} \right) = \sqrt {{\eta ^2} + {{\bar \eta }^2}} $ | (16) |
式中:
同样可近似按规则波的结果计算各时刻各位置的辐射应力,对以α角度入射的行进波,有
| $ S = {E_{\rm{w}}}\left( {x,t} \right)\left[ {\begin{array}{*{20}{c}} {n{{\cos }^2}\alpha + \frac{1}{2}\left( {2n - 1} \right)}&{\frac{n}{2}\sin 2\alpha }\\ {\frac{n}{2}\sin 2\alpha }&{n{{\sin }^2}\alpha + \frac{1}{2}\left( {2n - 1} \right)} \end{array}} \right] $ | (17) |
由不规则波辐射应力的计算表达式可知,相对不规则波辐射应力的精确计算方法,该近似方法得到的辐射应力结果有两处近似:一处来自式(17)中各时刻各位置的波能Ew(x, t)的计算,它是假定初始时刻的波能以峰频对应的传播速度cg向前传播近似得到;另一处来自式(17)中辐射应力计算表达式中的波能传递率n=(1+2kph/sinh2kph)/2,它是由峰频对应的波数近似计算得到。这种方法以峰频代替各组成波的频率,只有在窄波能谱的情况下才有较好的精度。该方法的优点是将不规则波近似看成规则波计算,原有的规则波结果可直接应用,计算速度比精确的计算方法要快得多。本文试验中的不规则波采用JONSWAP谱生成,通过后面的分析可知,试验所生成的不规则波也为窄波能谱,用该计算方法能快速达到较好精度的结果。
3 两种计算方法的分析比较为了分析不规则波辐射应力近似方法的计算精度和适用范围,这里采用改进的JONSWAP型谱[10]来生成不规则波,其表达式如下:
| $ S\left( f \right) = {\beta _j}H_{1/3}^2T_{\rm{p}}^{ - 4}{f^{ - 5}}\exp \left[ { - \frac{5}{4}{{\left( {{T_{\rm{p}}}f} \right)}^{ - 4}}} \right]\gamma \exp \left[ { - {{\left( {f/{f_{\rm{p}}} - 1} \right)}^2}/\left( {2{\sigma ^2}} \right)} \right] $ | (18) |
| $ {\beta _j} = \frac{{0.062\;38}}{{0.23 + 0.033\;6\gamma - 0.185\left( {1.9 + \gamma } \right) - 1}}\left( {1.094 - 0.019\;15\ln \gamma } \right) $ | (19) |
| $ {T_{\rm{p}}} = \frac{{{T_{{H_{1/3}}}}}}{{1 - 0.132{{\left( {\gamma + 0.2} \right)}^{ - 0.559}}}} $ | (20) |
式中:f为波浪频率;fp为谱峰频率;Tp为谱峰周期;TH1/3为有效周期;H1/3为有效波高;γ为谱峰因子;σ为峰型系数,当f≤fp时,σ取0.07,当f>fp时,σ取0.09。
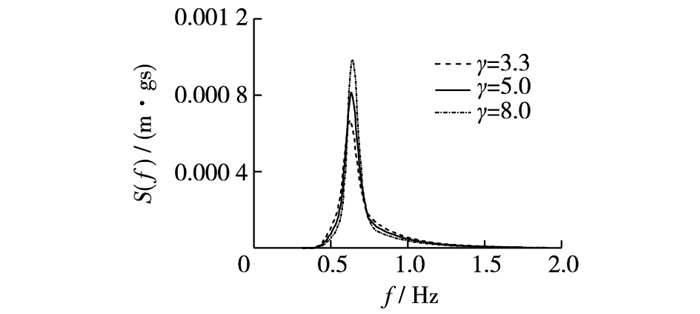
为了避免所模拟的组成波波浪频率成周期性重复,在各频率划分区间范围内随机选取频率作为该区间的代表频率。该谱式的优点在于一旦选定γ值,即可由设计波要素确定谱形。这里选取3个谱峰因子γ,其值分别为3.3,5.0和8.0来进一步分析比较,其他参数(TH1/3取1.5 s,H1/3取4.49 cm,水深h=0.045 m,波浪入射方向与岸线法线夹角α=30°)保持不变,由此得到不同谱峰因子γ对应的频谱图如图 2所示,谱峰因子γ值越大,相应的谱分布越窄。
|
图 2 不同谱峰因子γ对应的频谱 Figure 2 Spectrum diagrams for different spectral peak factors |
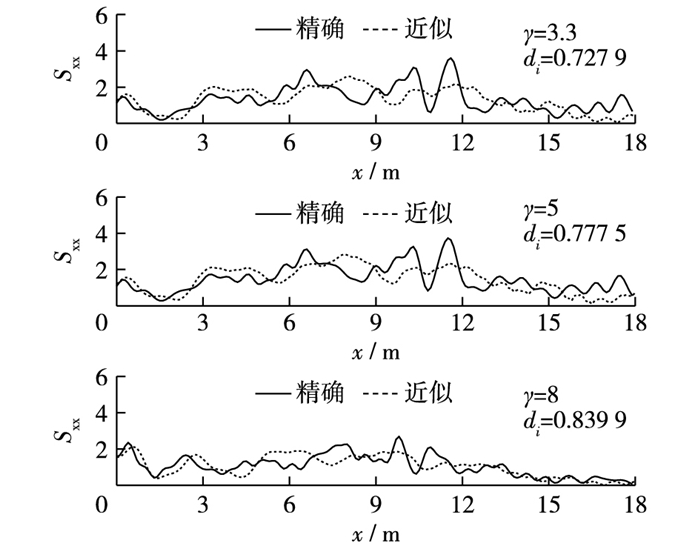
图 3给出了谱峰因子γ取值为3.3,5.0和8.0时,经初始位置x=0 m处(不规则波入射边界处)传播20 s后,不规则波辐射应力Sxx沿垂直岸方向精确计算结果与近似计算结果的比较。为衡量不规则波辐射应力近似计算结果与精确计算结果的接近程度,图中也给出了采用Wilmott[13]提出的统计参数di来加以判断,参数di值在0~1之间,值等于1表示二者完全吻合,其值越接近于1,二者结果越接近,其计算表达式为
| $ {d_i} = 1 - \frac{{\sum\limits_{i = 1}^N {{{\left( {\beta \left( i \right) - \alpha \left( i \right)} \right)}^2}} }}{{\left( {\sum\limits_{i = 1}^N {{{\left( {\left| {\beta \left( i \right) - \bar \alpha } \right| + \left| {\alpha \left( i \right) - \bar \alpha } \right|} \right)}^2}} } \right)}} $ | (21) |
|
图 3 不规则波辐射应力精确计算结果与近似计算结果比较 Figure 3 Comparison between accurate and approximate calculation results of irregular wave radiation stress |
式中:α(i)和β(i)分别为精确计算和近似计算方法对应的结果;
由图 3可见,随着谱峰因子γ值增大,谱分布变窄(图 2),统计参数di值由0.727 9逐渐增大到0.839 9,这表明谱分布越窄,不规则波辐射应力Sxx的近似计算方法与精确的计算方法计算结果更为接近。对于其他方向的辐射应力(Syy,Sxy)也有与其一致的规律,因篇幅所限,这里不再给出。总体而言,针对由JONSWAP谱(谱峰因子γ=3.30)产生不规则波的试验波况,不规则波辐射应力的近似计算方法与精确计算方法的结果也较吻合,误差较小(di >0.7)。但进一步比较会发现,不规则波波浪从入射边界(x=0 m)开始传播至离入射边界4 m(x=4 m)之间,不规则波辐射应力的精确计算与近似计算较为一致,当不规则波波浪从x=4 m位置继续向前传播后,精确计算方法计算所得的辐射应力结果相对近似计算结果有更多频率更高幅值更大的波动,这些波动能更能精准地反应各时刻各位置辐射应力的实际状况,这对于进一步研究沿岸流不稳定运动有重要意义。
4 波能近似计算方法试验验证通过由试验[12]所测波面升高时间历程转化得到的波能来验证本文波能近似计算方法的准确性。首先给出由试验测量得到的波面升高时间历程η(t)来确定所对应波能的方法。试验中沿垂直岸方向布置了浪高仪,可以用来记录各个位置的波面升高历程数据η(t),经Hilbert变换[10]可得η°(t),利用A(t)=(η2(t)+η°2(t))1/2可得波浪的波包线,进而由Ew(t)=1/2ρgA2(t)可求得浪高仪所在位置随时间变化的波能Ew(t)。
数值计算中,入射边界直接取离岸最远处第一个浪高仪(距离岸线22 m)所测的波面升高时间历程数据η(t)经转化后得到的随时间变化的波能Ew(t),按第2节中的近似处理方法,假定波群以峰频向前传播,由波能量守恒方程可计算得到任一时刻任一位置的波能Ew(t)。
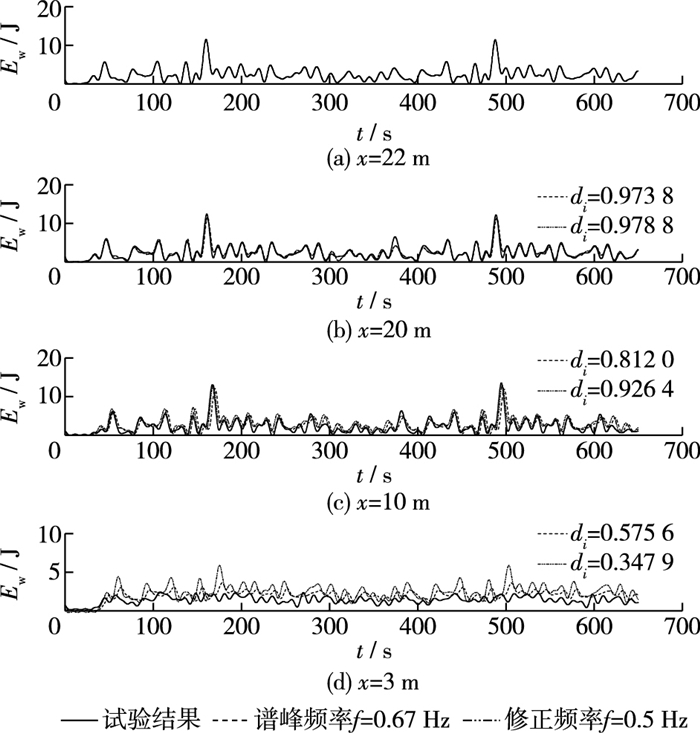
图 4给出了不规则波况(Tp=1.5 s, Hrms=4.49 cm)不同位置计算得到的波能和试验所测波面升高经Hilbert变换后所得的波能滤波(低通滤波截断频率为0.1 Hz)后值的比较。图 4(a)为距离岸线22 m处的波能,同时也是入射边界处的波能,二者重合;图 4(b)处于平底地形段,二者吻合较好,相应的峰值频率位置基本重合,能量大小也符合较好;图 4(c)处于平面斜坡地形段,此时波浪未破碎,二者吻合仍较好,但相对于平底地形段吻合稍差,表现为相应的峰值频率位置稍有偏差,能量大小偏差也比平底地形段大;图 4(d)处于平面斜坡地形段,此时波浪已破碎,二者偏差较大,试验结果中波能的高频峰值位置和能量大小,在数值计算结果中已很难与其一一对应,但数值计算结果基本能反映试验结果中的平均波能。总体来说,数值计算结果与试验结果吻合较好,尤其是在波浪破碎以前,这表明波能近似计算方法假定波群以峰频对应的波群速度向前传播是合理的,这其中各位置计算得到的峰频时间点和试验结果存在较小的时间差可进一步通过修正波群以接近峰频对应的波群速度向岸传播来减小误差,图 4也同时给出了修正传播频率fp=0.5Hz的计算结果,由图 4中距离岸线10 m处计算结果和试验结果的比较可知,波浪破碎前,修正后计算得到的峰频大小及时间点和试验结果更加接近。图 4中也给出了波能近似计算方法及其修正后的结果相对于试验测量转换得到的波能结果接近程度的统计参数di。通过比较可发现,修正后的di的值大于修正前的结果,但波浪破碎后没有得到改善,这和前面描述的结论一致。故在以后的不规则波辐射应力计算时,可采用近似计算方法来实现快速计算,同时也能得到较好的计算精度。需要指出的是波浪破碎后,两种数值计算结果均与试验结果有较大偏差(di < 0.6),主要是由于波浪破碎能量耗散模型很难准确地模拟波浪破碎过程所致。
|
图 4 波能近似计算方法和试验所得的波能滤波后比较 Figure 4 Comparison of wave energy after filtering between approximation calculation method and experimental result |
本文给出不规则波作用下辐射应力的精确计算方法和近似计算方法,对两种计算方法进行了分析比较,并用试验结果对近似计算方法中的波能计算进行了进一步验证。结果表明:窄谱情况下,近似计算方法已拥有较好的精度,可节省大量计算时间,从而大幅提高计算效率,针对由JONSWAP谱(谱峰因子γ取3.3以上)产生不规则波,均可看作是窄谱情况,尤其当数值计算网格很多,计算平均沿岸流场时可直接采用不规则波辐射应力的近似计算方法。精确计算方法的计算速度远远慢于近似计算方法,但它更能精准地反应各时刻各位置辐射应力的波动状况,这能更好地解释沿岸流运动过程中某些不稳定波动现象,对于进一步研究沿岸流不稳定运动有重要意义。
| [1] |
VISSER P J. Laboratory measurements of uniform longshore currents[J]. Coastal Engineering, 1991, 15(5): 563-593. |
| [2] |
WANG Yan, ZOU Zhili. An experimental and numerical study of bimodal velocity profile of longshore currents over mild-slope barred beaches[J]. Ocean Engineering, 2015, 106: 415-423. DOI:10.1016/j.oceaneng.2015.06.038 |
| [3] |
陈志春. 波流耦合作用下近岸流现象研究[D]. 天津: 天津大学, 2005. (CHENG Zhichun. Research on nearshore currents with wave-current interaction[D]. Tianjin: Tianjin University, 2005. (in Chinese))
|
| [4] |
刘秋兴, 于福江, 王培涛, 等. 辐射应力对台风风暴潮预报的影响和数值研究[J]. 海洋学报, 2011, 33(5): 47-53. ( LIU Qiuxing, YU Fujiang, WANG Peitao, et al. Numerical study on storm surge forecasting considering wave-induced radiation stress[J]. Acta Oceanologica Sinica, 2011, 33(5): 47-53. (in Chinese)) |
| [5] |
郑金海, 严以新. 波浪辐射应力理论的应用和研究进展[J]. 水利水电科技进展, 1999, 19(6): 6-8. ( ZHENG Jinhai, YAN Yixin. Research and application of wave-induced radiation stress theory[J]. Advances in Science and Technology of Water Resources, 1999, 19(6): 6-8. (in Chinese)) |
| [6] |
郑金海, 严以新. 波浪辐射应力张量的垂向变化[J]. 水动力学研究与进展, 2001, 16(2): 246-253. ( ZHENG Jinhai, YAN Yixin. Vertical variations of wave-induced radiation stresses tensor[J]. Journal of Hydrodynamics, 2001, 16(2): 246-253. (in Chinese)) |
| [7] |
LONGUET-HIGGINS M S, STEWART R W. Radiation stresses in water waves; a physical discussion with applications[J]. Deep Sea Research and Oceanographic Abstracts, 1964, 11(4): 529-562. DOI:10.1016/0011-7471(64)90001-4 |
| [8] |
李孟国, 时钟, 李文丹. 综合考虑多种变形因素的近岸多向不规则波传播数学模型—Ⅰ.模型的建立[J]. 水动力学研究与进展, 2006, 21(4): 444-450. ( LI Mengguo, SHI Zhong, LI Wendan. A mathematical model for irregular multi-directional wave propagation incorporating multi-factors of transformation in the coastal waters—Ⅰ. setup of the model[J]. Journal of Hydrodynamics, 2006, 21(4): 444-450. (in Chinese)) |
| [9] |
唐军, 沈永明, 崔雷, 等. 随机波浪作用下近岸波流场的数值模拟[J]. 力学学报, 2008, 40(4): 454-463. ( TANG Jun, SHEN Yongming, CUI Lei, et al. Numerical simulation of random wave-induced near-short currents[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(4): 454-463. (in Chinese)) |
| [10] |
俞聿修. 随机波浪及其工程应用[M]. 大连: 大连理工大学出版社, 2003. ( YU Yuxiu. Random wave and its engineering application[M]. Dalian: Dalian University of Technology Press, 2003. (in Chinese))
|
| [11] |
郑永红, 沈永明, 邱大洪. 结合抛物型缓坡方程计算波浪辐射应力[J]. 海洋学报, 2000, 22(6): 110-116. ( ZHENG Yonghong, SHEN Yongming, QIU Dahong. Calculation of wave radiation stresses connected with the parabolic mild-slope equation[J]. Acta Oceanologica Sinica, 2000, 22(6): 110-116. (in Chinese)) |
| [12] |
沈良朵, 邹志利, 唐志波, 等. 缓坡海岸平均沿岸流实验研究与数值模拟[J]. 船舶力学, 2016, 20(8): 973-982. ( SHEN Liangduo, ZOU Zhili, TANG Zhibo, et al. Experimental study and numerical simulation of mean longshore current for mild slope[J]. Journal of Ship Mechanics, 2016, 20(8): 973-982. (in Chinese)) |
| [13] |
WILMOTT C J. On the validation of models[J]. Physical Geography, 1981, 2(2): 184-194. |
2. State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China;
3. Ocean Engineering, Zhejiang University, Hangzhou 310058, China
 2018
2018 
