2. 南京水利科学研究院 水文水资源与水利工程科学国家重点实验室,江苏 南京 210029;
3. 汉江水利水电(集团)有限责任公司水库调度中心,湖北 武汉 430048
洪水灾害是当今世界上最严重的自然灾害之一,防洪减灾研究一直是世界各国政府与学术界所普遍关注的重大问题[1-2]。洪灾风险评估是防洪减灾领域的重要基础性工作[3-4]。从洪灾的形成机制看,致灾因子危险性、承灾体脆弱性和洪灾损失风险三者及其关系,组成了洪灾风险系统[5-6],其中承灾体脆弱性是联系致灾因子危险性和洪灾损失风险的重要桥梁,是洪灾风险评估的关键部分[5, 7],因此分析洪灾脆弱性对于减少洪灾损失意义重大。洪灾脆弱性分析旨在分析自然、经济、社会与环境系统之间的相互耦合作用及其对洪灾的驱动力、抑制作用和响应能力,其主要内容包括承灾体暴露性、敏感性和防灾减灾能力三个方面[8-9]。
对脆弱性的研究,始于20世纪80年代,源于对当时学术界盛行的致灾因子论的反思[10]。1975年,G.F.White首次将防灾减灾研究从单纯致灾因子分析扩展到人类自身面对洪灾时的脆弱性[11]。此后,灾害的研究逐渐关注自然环境、社会、经济等因素,如Cutter等通过将美国卡罗来纳州南部乔治敦郡的自然脆弱性与社会脆弱性的空间差异分布图进行叠置, 分析了该区域的灾害脆弱性[12]。汪朝辉等选取汛期降雨量、单位面积生产总值、易涝面积、水田占总土地面积的比例,森林覆盖率,人均国内生产总值,单位面积水库和塘坝总库容这7项指标,通过数学模型对湖南省119个县(市)进行洪灾脆弱性评估[13]。葛怡等利用Hoovering改进模式,评价了长沙地区水灾社会脆弱性[14]。殷杰等构建了上海黄浦江流域的7种主要承灾体经济损失脆弱性方程和人口脆弱性方程,分析了上海黄浦江流域风暴洪水经济损失和人口脆弱性分布[10]。郭凤清等通过各类承灾体的洪灾损失和洪水特征之间的关系,分析了潖江蓄洪区承载体脆弱性[15]。
目前有关洪灾脆弱性评价的方法主要包括曲线法和指标体系法两类。洪灾脆弱性曲线法是依据已发生洪水灾情建立的脆弱性曲线来评价区域洪灾脆弱性,分析结果与事实较为吻合。但由于脆弱性曲线的建立,需要大量的洪灾损失数据,这些资料往往难以获取,且计算结果往往是资料统计单元的区域整体洪灾脆弱性,不能反映洪灾脆弱性在区域内的空间差异,也难以建立未发生洪水灾害区域的脆弱性曲线[7-8]。指标体系法,基于洪灾脆弱性指标体系计算洪灾脆弱性指数,立足于洪灾脆弱性结构要素之间的层次性和关联性,对数据资料要求低、操作简便,也能反映区域洪灾脆弱性的整体宏观状况[16]。但该类方法因在评价指标选择、指标权重确定等方面带有一定程度主观性,从而影响评价结果的准确性[14]。为此,本文运用突变理论,采用突变级数综合评价法对洪灾脆弱性进行评价,该方法汲取了指标体系法的优点,且只需考虑各评价指标间的相对重要性,无需确定各评价指标的具体权重值,即可实现合理评价,避免了确定评价指标权重值的主观性[17-21]。同时,相比于其他洪灾脆弱性评价方法,突变级数综合评价法过程清晰,计算简单,更便于实际应用。
1 基于突变理论的区域洪灾脆弱性评价方法 1.1 突变理论基本思想突变理论是20世纪70年代发展起来的,以奇点理论、拓扑学及结构稳定性等数学理论为基础,主要研究自然界和社会现象中的各种形态、结构的非连续性突变的新数学学科。突变理论用一组参数描述系统所处的状态,当系统处于稳定状态时,该系统状态函数取一个极值;当参数在某个范围内变化,该函数有不止一个极值时,系统必然就处于不稳定状态,所以可以通过计算状态函数的极值来考察某一系统是否稳定[17]。其中,描述系统状态的函数称为势函数,称势函数导数为零的点为临界点,在三维空间中,临界点构成的曲面称为临界曲面(或平衡曲面);可能出现突变的因素称为状态变量,引发突变的因素称为控制变量。雷内·托姆用拓扑学理论证明了势函数的不同性质取决于控制变量的个数,当控制变量个数不大于4时,势函数有7种形式,称其为突变理论的7种突变模型,这7种突变模型被统称为初等突变模型[18]。7种初等突变模型中,最常用的是尖点型突变、燕尾型突变和蝴蝶型突变(见表 1)。
| 表 1 三类常用的初等突变模型 Table 1 Three commonly used models of elementary catastrophe |
在初等突变模型中,对势函数V(x)求一阶导数,并令V′(x)=0,得到临界点方程,对势函数V(x)求二阶导数,并令V″(x)=0,得到奇点集方程[19]。将两方程联立消除x后,可推导出分歧集方程[19](见表 1)。由于初等突变模型中各控制变量和状态变量的取值范围不一致,不可直接采用分歧方程进行评价计算,需对其进行归一化处理[20]。归一化公式是初等突变模型进行综合评价的基本运算公式,针对不同的突变模型归一化公式如下[21]:
| $ 尖点突变:{X_a} = {a^{1/2}}, {\rm{ }}{X_b} = {b^{1/3}} $ | (1) |
| $ 燕尾突变:{X_a} = {a^{1/2}}, {X_b} = {b^{1/3}}, {\rm{ }}{X_c} = {c^{1/4}} $ | (2) |
| $ 蝴蝶突变:{X_a} = {a^{1/2}}, {\rm{ }}{X_b} = {b^{1/3}}, {X_c} = {c^{1/4}}, {X_d} = {d^{1/5}} $ | (3) |
基于突变理论的区域洪灾脆弱性评价方法是以初等突变模型演化出来的多目标综合评价和多准则决策方法,其计算步骤如下:
(1) 建立区域洪灾脆弱性评价指标体系。根据系统形成机制建立评价指标体系,对于难以量化的一维控制量指标可将其分解为若干层可以实测的多维指标,依据逻辑分类分出各指标的主次关系,按照先主后次的原则构建树状递阶层次结构模型。由洪灾脆弱性组成结构出发,从暴露性、敏感性、防灾减灾能力3个方面选取指标构建洪灾脆弱性评价指标体系。暴露度反映了研究对象对洪水的暴露程度,敏感性反映了研究对象易于受洪灾影响的程度,防灾减灾能力反映了研究对象应对洪灾的能力和从灾害事件中恢复的能力[22]。论文借鉴相关研究成果[11, 13, 22-23],根据研究区域的自然与社会经济发展特点,以及数据的可获得性,共选择11个变量作为评价指标,见表 2。
| 表 2 洪灾脆弱性评价指标体系 Table 2 Evaluation index system of flood vulnerability |
(2) 评价指标一致无量纲化处理[24]。对评价指标数据进行一致无量纲化处理,将其转变为0~1之间的正向指标。对于越大越优型评价指标,采用式(4)处理:
| $ {r_{ij}} = [{x_{ij}}-{\rm{min}}({x_{ij}})\left] / \right[{\rm{max}}({x_{ij}})-{\rm{min}}({x_{ij}})] $ | (4) |
对于越小越优型评价指标,采用式(5)处理:
| $ {r_{ij}} = [{\rm{max}}({x_{ij}})-{x_{ij}}\left] / \right[{\rm{max}}({x_{ij}})-{\rm{min(}}{x_{ij}})] $ | (5) |
式中:max(xij),min(xij)分别为同一评价指标下不同评价对象的评价指标值xij中的最大值和最小值。
(3) 利用归一化公式进行综合评价[25]。根据建好的区域洪灾脆弱性评价指标体系,选取初等突变模型,并利用归一化公式,由最底层向最终评价目标层进行递归运算,求出总突变级数进行评价。在进行各层次突变级数计算时需遵循两条准则。非互补准则:评价指标之间作用不可互相替代时,按“大中取小”原则取值作为上层指标值;互补准则:评价指标之间可相互弥补其不足时,取其均值作为上层指标值[19]。
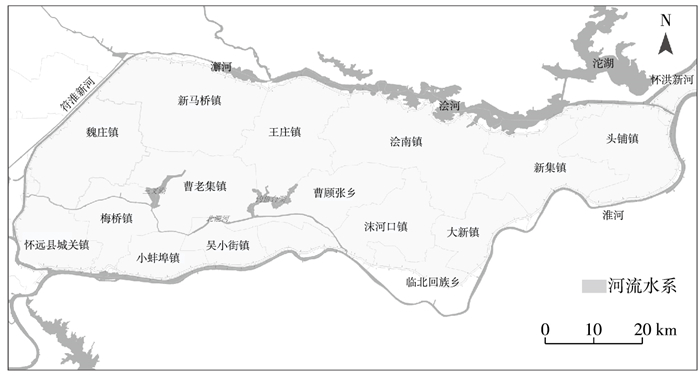
2 实例研究怀洪南片防洪保护区是全国重点防洪保护区之一,位于安徽省境内,是淮河左堤及怀洪新河右堤保护的区域,面积约为1 480 km2,防洪保护区内涉及1区3县15个乡镇(如图 1)[26]。怀洪南片防洪保护区地势总体趋势是北高南低。固镇县、怀远县城和五河县浍南镇地面高程较高,高程在19.0 m左右,低洼地区主要分布在钓鱼台湖河及五河县城附近地区,高程为13.0~14.0 m,其他区域高程为15.0~16.0 m。防洪保护区内降雨集中,汛期6—9月降水量占年降水量的50%~75%,暴雨强度大、持续时间长、范围大且洪水总量大,往往形成流域性暴雨洪水。怀洪南片防洪保护区分别于1950,1952,1954,1956,1962,1963,1965,1990,1991,1996,1998,2001,2003,2005,2007年发生较大洪水15次,平均约4年一次,洪涝灾害损失严重,因此,对怀洪南片防洪保护区进行合理的洪灾管理势在必行。洪灾脆弱性反映了暴露于洪水中的承灾体易于遭受洪水破坏和从洪灾中恢复的能力,对洪灾脆弱性进行分析评价,可确定研究区各乡镇的洪灾脆弱性程度和空间分布,为怀洪南片防洪保护区的洪灾管理提供指导,对于防洪减灾具有重要的意义。根据数据的可获得性,以乡镇作为评价单元进行洪灾脆弱性评价。表 3是依据《2015年蚌埠市统计年鉴》数据经过空间处理获得的各评价单元的评价指标数据集。
|
图 1 怀洪南片防洪保护区研究范围 Figure 1 Study area of Huaihongnanpian flood protection area |
| 表 3 研究区评价指标原始数据 Table 3 Original data of evaluation index in study area |
首先,将表 3的各指标原始数值运用式(4)和(5)进行一致无量纲化处理,转换成[0, 1]范围内的正向指标,然后根据突变理论递归运算的准则,运用归一公式逐层进行归一化运算处理,直至得到最高层评价指标,评价结果见表 4。以怀远县城关镇为例,具体计算过程如下。
| 表 4 各乡镇洪灾脆弱性指标值 Table 4 Flood vulnerability index values of each township |
由表 1可知,最底层指标C1,C2,C3,C4构成蝴蝶突变,根据式(3)有:XC1=(0.237 339)1/2=0.487 174,XC2=(0.518 119)1/3=0.803 174,XC3=(1)1/4 =1,XC4=(0)1/5=0,由于各控制变量之间可以互相弥补不足,综合起来共同对上一层评价指标产生作用,因此按“互补准则”取均值,得B1=(XC1+XC2+XC3+XC4)/4= 0.572 587。同理可计算出B2=0.323 419,B3=0.828 588。同样,准则层B1,B2,B3构成燕尾突变,根据式(2)有:XB1=(0.572 587)1/2=0.756 694,XB2=(0.323 419)1/3=0.686 417,XB3=(0.828 588)1/4 =0.954 079,按照“互补准则”,求得怀远县城关镇最终的洪灾脆弱性指标值为0.799 1。其余各镇以此类推,可求得洪灾脆弱性评价指标值(见表 4)。
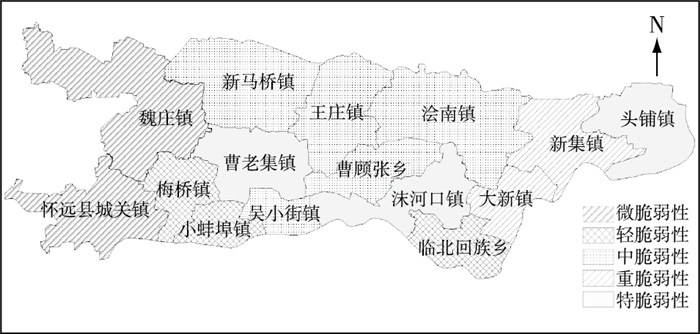
2.2 洪灾脆弱性等级的确定将洪灾脆弱性指数在ArcGIS中采用自然断点法分为5级:微脆弱性(Ⅰ)、轻脆弱性(Ⅱ)、中脆弱性(Ⅲ)、重脆弱性(Ⅳ)和特脆弱性(Ⅴ),各等级的取值区间分别为[0.799 1, 0.827 7],[0.839 4,0.859 8],[0.884 8,0.897 1],[0.908 1,0.914 1],[0.919 6,0.928 7],防洪保护区洪灾脆弱性等级空间分布如图 2所示。洪灾脆弱性等级结果见表 4。
|
图 2 研究区洪灾脆弱性空间分布 Figure 2 Spatial distribution of flood vulnerability in study area |
为验证突变级数综合评价法评价结果的可靠性,本文将基于熵权的模糊优选法应用到研究区15个乡镇的洪灾脆弱性评价中[24, 27-28]。基于熵权的模糊优选法结合了熵权法和模糊优选法的优点,利用评价对象的评价指标构成的特征值矩阵来确定权重及相对优属度,计算结果无主观因素的影响,科学客观。在本实例中,使用基于熵权的模糊优选法时,评价指标、一致无量纲处理公式和指标间的相对重要性关系与突变级数综合评价法完全一致。具体评价步骤为:首先将表 3的数据利用式(4)和式(5)进行一致无量纲化处理,得到相对优属度矩阵,然后根据文献[18]中计算熵权的式(6.40),(6.42)和(6.43)确定权重,最后将计算的权重代入文献[18]的式(6.35)确定各乡镇洪灾脆弱性优先顺序。计算得洪灾脆弱性评价指标值见表 4,洪灾脆弱性等级的确定同样使用自然断点法(见表 4)。
由表 4可以看出,对于这两种洪灾脆弱性评价方法,除了小蚌埠镇、临北回族乡、曹顾张乡、大新镇及吴小街镇这5个乡镇的洪灾脆弱性等级存在细微差别外,其他乡镇的洪灾脆弱性等级完全一致,这在一定程度上验证了突变级数综合评价法计算结果的可靠性。
突变级数综合评价法结果表明:研究区15个乡镇中,微脆弱性等级的乡镇有2个,怀远县城关镇和魏庄镇,占研究区总面积的21.3%;轻脆弱性等级的乡镇有3个,小蚌埠镇、梅桥镇和临北回族乡,占研究区总面积的11.2%;中脆弱性等级的乡镇有5个,分别为新马桥镇、王庄镇、曹顾张乡、浍南镇和吴小街镇,占研究区总面积的36.6%;重脆弱性等级的乡镇有2个,大新镇和新集镇,占研究区总面积的10.7%;特脆弱性等级的乡镇有3个,曹老集镇,头铺镇和沫河口镇,占研究区总面积的20.2%。中等及中等脆弱性以上的乡镇面积占研究区总面积的67.5%,说明怀洪南片防洪保护区内大部分地区的洪灾脆弱性程度偏高。
由表 4可见,除了小蚌埠镇和吴小街镇的防灾减灾能力指标明显小之外,其余乡镇防灾减灾能力指标大致相同,说明防灾减灾能力不是影响洪灾脆弱性水平的主导要素。暴露度指数高的乡镇有小蚌埠镇、吴小街镇、曹老集镇、头铺镇和沫河口镇,其中,小蚌埠镇和吴小街镇的防灾减灾能力指标明显小于其他乡镇,降低了二者的洪灾脆弱性水平。怀远县城关镇,魏庄镇和梅桥镇的敏感性指标较其他乡镇相比低,且暴露度指标也低,也就是说这3个乡镇暴露于洪灾中的可能性小,也不易于受洪水影响,3个乡镇的洪灾脆弱性处于中等偏下水平。
特脆弱性等级的乡镇是头铺镇、沫河口镇和曹老集镇。怀洪南片防洪保护区地势北高南低,低洼地区主要分布在北淝河、钓鱼台湖及五河县城附近地区,当洪水灾害发生时,地处低洼地势的头铺镇、沫河口镇、曹老集镇容易被洪水淹没,暴露于洪水中。同时,这3个乡镇的农业人口比重大,经济以农业为主,当汛期发生洪涝灾害时,农作物易于受洪水影响而减产,导致经济损失。以上分析表明,研究区内洪灾脆弱性水平高的地区,地势低,承灾体容易暴露于洪灾之中,且受灾区内承灾体易于受洪水影响,整体防灾抗灾水平不高。
微脆弱性等级的乡镇是怀远县城关镇和魏庄镇。怀远县城关镇和魏庄镇地势较高,高程约为18.48 m,承灾体暴露度低。怀远县城关镇经济以工业和第三产业为主,农业比重很低,对洪灾的敏感性低,汛期暴雨洪水对其威胁小。同时,怀远县城关镇地处县城,路网发达,避难所及医疗救助机构密集,对洪灾的防御和适应能力较高。而魏庄镇虽然经济以农业为主,但其所处地势高,在很大程度上削弱了洪灾对其造成的影响,降低了魏庄镇的洪灾脆弱性等级。
根据研究区洪灾脆弱性组成和分布,可因地制宜地采取不同措施降低各乡镇的洪灾脆弱性。例如吴小街镇,该镇经济水平较高,有一定的防灾减灾能力,但其暴露度和敏感性指数高,要降低吴小街镇的洪灾脆弱性水平,可通过加高堤防或改善种植结构和生产模式等方式。洪灾脆弱性等级中等以上的乡镇,例如头铺镇,暴露度,敏感性及防灾减灾能力指数都较高,需要采取综合措施降低洪灾脆弱性水平,如加高堤防,增强农田基础建设及河流渠道输排水能力,调整区域农作物种植结构,完善洪水预警机制和救灾应急预案,加强洪灾自救的宣传工作等。
3 结语(1) 从20世纪70年代至今,突变理论已经有40余年的发展历程,经过这40多年的不断探索和完善,突变理论已经具有相当深厚的数学基础,在其概念和方法被越来越普遍地理解和接受的同时,突变理论在实际生产中的应用也越来越广泛。突变级数综合评级法作为一种多指标评价方法,其指标值的量化是根据各指标在归一公式中的内在作用机理进行的,无需确定具体的指标权重,减少了主观因素的影响,使评价结果更趋于实际。较其他评价方法而言,突变级数综合评价法过程清晰,计算简单,更便于实际应用。
(2) 本文采用突变级数综合评价法得到的计算结果与基于熵权的模糊优选法计算结果非常接近,且经分析与怀洪南片防洪保护区实际情况相吻合,验证了突变级数综合评价法的合理性和准确性,为区域洪灾脆弱性评价提供了一种新方法。
(3) 突变级数综合评价法计算结果表明,怀洪南片防洪保护区内大部分地区的洪灾脆弱性程度偏高,其中特脆弱性等级的乡镇为头铺镇、沫河口镇、曹老集镇,重脆弱性等级的乡镇为大新镇、新集镇,中脆弱性等级的乡镇为新马桥镇、王庄镇、曹顾张乡、浍南镇、吴小街镇,轻脆弱性等级的乡镇为小蚌埠镇、梅桥镇、临北回族乡,微脆弱性等级的乡镇为怀远县城关镇、魏庄镇。经分析,地势的高低及农业比重的大小对洪灾脆弱性影响较大,故对防洪保护区的各乡镇进行洪灾管理时,要重点关注处于低洼地势并以农业为主的乡镇的防洪减灾工作,可通过增强农田基础建设及河流渠道输排水能力,调整区域农作物种植结构,合理分配物资和管理投入力度等措施降低高脆弱性乡镇的脆弱性水平。所以,研究成果对于降低防洪保护区内各乡镇的洪灾脆弱性具有指导作用,对防洪保护区的减灾投资及洪灾管理具有重要意义。
| [1] |
毛德华, 何梓霖, 贺新光, 等. 洪灾风险分析的国内外研究现状与展望(Ⅰ)——洪水为害风险分析研究现状[J]. 自然灾害学报, 2009, 18(1): 139-149. ( MAO Dehua, HE Zilin, HE Xinguang, et al. Review and prospect of research on flood risk analysis at home and abroad(Ⅰ): status quo of research on risk analysis of flood hazard[J]. Journal of Natural Disasters, 2009, 18(1): 139-149. (in Chinese)) |
| [2] |
邹强. 洪灾风险综合分析与智能评价的理论与方法[D]. 武汉: 华中科技大学, 2013. (ZOU Qiang. Study on the theory and method of comprehensive analysis and intelligent assessment of flood disaster risk[D]. Wuhan: Huazhong University of Science and Technology, 2013. (in Chinese))
|
| [3] |
魏一鸣, 杨存键, 金菊良. 洪水灾害分析与评估的综合集成方法[J]. 水科学进展, 1999, 10(1): 25-30. ( WEI Yiming, YANG Cunjian, JIN Juliang. Integrated method for analysis and evaluation of flood disaster[J]. Advances in Water Science, 1999, 10(1): 25-30. (in Chinese)) |
| [4] |
魏一鸣, 范英, 金菊良. 洪水灾害风险分析的系统理论[J]. 管理科学学报, 2001, 4(2): 7-11, 44. ( WEI Yiming, FAN Ying, JIN Juliang. System theory of flood disaster risk analysis[J]. Journal of Management Sciences in China, 2001, 4(2): 7-11, 44. (in Chinese)) |
| [5] |
金菊良, 宋占智, 周玉良, 等. 水旱灾害风险评估方法体系及其实证研究[J]. 水利水电科技进展, 2015, 35(5): 142-151. ( JIN Juliang, SONG Zhanzhi, ZHOU Yuliang, et al. Risk assessment method system for flood and drought disasters and its application[J]. Advances in Science and Technology of Water Resources, 2015, 35(5): 142-151. DOI:10.3880/j.issn.1006-7647.2015.05.020 (in Chinese)) |
| [6] |
金菊良, 郦建强, 周玉良, 等. 旱灾风险评估的初步理论框架[J]. 灾害学, 2014, 29(3): 1-10. ( JIN Juliang, LI Jianqiang, ZHOU Yuliang, et al. Research on the theoretical framework of drought risk assessment[J]. Journal of Catastrophology, 2014, 29(3): 1-10. (in Chinese)) |
| [7] |
石勇, 许世远, 石纯, 等. 洪水灾害脆弱性研究进展[J]. 地理科学进展, 2009, 28(1): 41-46. ( SHI Yong, XU Shiyuan, SHI Chun, et al. A review on development of vulnerability assessment of floods[J]. Progress in Geography, 2009, 28(1): 41-46. DOI:10.11820/dlkxjz.2009.01.006 (in Chinese)) |
| [8] |
KARAGIORGOS K, THALER T, HVBL J, et al. Multi-vulnerability analysis for flash flood risk management[J]. Natural Hazards, 2016, 82(1): 1-25. DOI:10.1007/s11069-016-2176-5 |
| [9] |
周扬, 李宁, 吴文祥. 自然灾害社会脆弱性研究进展[J]. 灾害学, 2014, 29(2): 128-135. ( ZHOU Yang, LI Ning, WU Wenxiang. Research progress on social vulnerability to natural disasters[J]. Journal of Catastrophology, 2014, 29(2): 128-135. (in Chinese)) |
| [10] |
殷杰, 尹占娥, 于大鹏, 等. 风暴洪水主要承灾体脆弱性分析——黄浦江案例[J]. 地理科学, 2012, 32(9): 1155-1160. ( YIN Jie, YIN Zhan'e, YU Dapeng, et al. Vulnerability analysis for storm induced flood: a case study of huangpu river basin[J]. Scientia Geographica Sinica, 2012, 32(9): 1155-1160. (in Chinese)) |
| [11] |
游温娇, 张永领. 洪灾社会脆弱性指标体系研究[J]. 灾害学, 2013, 28(3): 215-220. ( YOU Wenjiao, ZHANG Yongling. Research on index system of social vulnerability for flood hazard[J]. Journal of Catastrophology, 2013, 28(3): 215-220. (in Chinese)) |
| [12] |
CUTTER S L, MITCHELL J T, SCOTT M S. Revealing the vulnerability of people and places: a case study of Georgetown County, South Carolina[J]. Annals of the Association of American Geographers, 2015, 90(4): 713-737. |
| [13] |
汪朝辉, 王克林, 熊鹰, 等. 湖南省洪涝灾害脆弱性评估和减灾对策研究[J]. 长江流域资源与环境, 2003, 12(6): 586-592. ( WAN Zhaohui, WANG Kelin, XIONG Ying, et al. Assessment of the vulnerability of flood-waterlogging disaster and countermeasures of disaster reduction in Hunan province[J]. Resources and Environment in the Yangtze Basin, 2003, 12(6): 586-592. (in Chinese)) |
| [14] |
葛怡, 史培军, 刘婧, 等. 中国水灾社会脆弱性评估方法的改进与应用—以长沙地区为例[J]. 自然灾害学报, 2005, 14(6): 54-58. ( GE Yi, SHI Peijun, LIU Jing, et al. Improvement and application of vulnerability assessment methodology for flood hazards in China: using Changsha prefecture as a case study[J]. Journal of Natural Disasters, 2005, 14(6): 54-58. (in Chinese)) |
| [15] |
郭凤清, 曾辉, 丛沛桐, 等. 潖江蓄洪区洪灾承灾体脆弱性分析[J]. 灾害学, 2014, 29(3): 102-107. ( GUO Fengqing, ZENG Hui, CONG Peitong, et al. Vulnerability analysis of hazard-affected bodies in Pajiang flood storage area[J]. Journal of Catastrophology, 2014, 29(3): 102-107. (in Chinese)) |
| [16] |
樊运晓, 罗云, 陈庆寿. 承灾体脆弱性评价指标中的量化方法探讨[J]. 灾害学, 2000, 15(2): 78-81. ( FAN Yunxiao, LUO Yun, CHEN Qingshou. Discussion on quantification method of evaluating vulnerability indexes of hazard bearing body[J]. Journal of Catastrophology, 2000, 15(2): 78-81. (in Chinese)) |
| [17] |
张业民. 突变理论在岩土与结构工程中的若干应用[D]. 大连: 大连理工大学, 2008. (ZHANG Yeming. Catastrophe theory applied in several geo-technic and structure engineering area[D]. Dalian: Dalian University of Technology, 2008. (in Chinese))
|
| [18] |
范留明, 耿鹏超. 突变理论在边坡工程应用的研究进展[J]. 地球科学进展, 2015, 30(11): 1268-1277. ( FAN Liuming, GENG Pengchao. The application and research progress of catastrophe theory in slope engineering[J]. Advances in Earth Sci-ence, 2015, 30(11): 1268-1277. (in Chinese)) |
| [19] |
李绍飞, 孙书洪, 王向余. 突变理论在海河流域地下水环境风险评价中的应用[J]. 水利学报, 2007, 38(11): 1312-1317. ( LI Shaofei, SUN Shuhong, WANG Xiangyu. Application of catastrophe theory to risk assessment of groundwater environment for river basin[J]. Journal of Hydraulic Engineering, 2007, 38(11): 1312-1317. DOI:10.3321/j.issn:0559-9350.2007.11.007 (in Chinese)) |
| [20] |
刘聚涛, 高俊峰, 姜加虎, 等. 基于突变理论的太湖蓝藻水华危险性分区评价[J]. 湖泊科学, 2010, 22(4): 488-494. ( LIU Jutao, GAO Junfeng, JIANG Jiahu, et al. Catastrophe theory based risk evaluation of blue-green algae bloom of different regions in Lake Taihu[J]. Journal of Lake Science, 2010, 22(4): 488-494. (in Chinese)) |
| [21] |
周绍江. 突变理论在环境影响评价中的应用[J]. 人民长江, 2003, 34(2): 52-54. ( ZHOU Shaojiang. Application of catastrophe theory in environmental impact assessment[J]. Yangtze River, 2003, 34(2): 52-54. (in Chinese)) |
| [22] |
陈萍, 王兴玲, 陈晓玲. 基于栅格的鄱阳湖生态经济区洪灾脆弱性评价[J]. 地理科学, 2012, 32(8): 958-964. ( CHEN Ping, WANG Xingling, CHEN Xiaoling. Flood vulnerability assessment of Poyang Lake economical ecological zone at raster level[J]. Scientia Geographica Sinica, 2012, 32(8): 958-964. (in Chinese)) |
| [23] |
李绍飞, 冯平, 孙书洪. 突变理论在蓄滞洪区洪灾风险评价中的应用[J]. 自然灾害学报, 2010, 19(3): 132-138. ( LI Shaofei, FENG Ping, SUN Shuhong. Application of catastrophe theory to evaluation of flood risk in detention basin[J]. Journal of Natural Disasters, 2010, 19(3): 132-138. (in Chinese)) |
| [24] |
方国华, 黄显峰. 多目标决策理论、方法及其应用[M]. 北京: 科学出版社, 2011. ( FANG Guohua, HUANG Xianfeng. Multi-objective decision theory, method and application[M]. Beijing: Science Press, 2011. (in Chinese))
|
| [25] |
李继清, 张玉山, 纪昌明, 等. 突变理论在长江流域洪灾综合风险社会评价中的应用[J]. 武汉大学学报(工学版), 2007, 40(4): 26-30. ( LI Jiqing, ZHANG Yushan, JI Changming, et al. Application of catastrophe theory to social assessment of integrated flood disaster risks in Yangtze River[J]. Engineering Journal of Wuhan University, 2007, 40(4): 26-30. (in Chinese)) |
| [26] |
南京水利科学研究院. 怀洪南片防洪保护区洪水风险图编制成果报告[R]. 南京: 南京水利科学研究院, 2016. (Nanjing Hydraulic Research Institute. Flood risk map compilation report of Huaihongnanpian flood protection area[R]. Nanjing: Nanjing Hydraulic Research Institute, 2016. (in Chinese))
|
| [27] |
张欣, 王宏丽, 李凯, 等. 熵权法及模糊优选法在日光温室墙体综合性能评价中的应用[J]. 中国农业大学学报, 2015, 20(5): 235-240. ( ZHANG Xin, WANG Hongli, LI Kai, et al. The application of weighted entropy and fuzzy optimization method in the evaluation of comprehensive performance of north wall in Chinese green house[J]. Journal of Chinese Agricultural University, 2015, 20(5): 235-240. (in Chinese)) |
| [28] |
陈艳萍, 吴凤平, 吴丹. 基于模糊优选和TOPSIS法的流域初始水权分配模型[J]. 河海大学学报(自然科学版), 2009, 37(4): 467-471. ( CHEN Yanping, WU Fengping, WU Dan. Initial water rights allocation model for basins based on fuzzy optimization and TOPSIS methods[J]. Journal of Hohai University(Natural Sciences), 2009, 37(4): 467-471. (in Chinese)) |
2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing Hydraulic Research Institute, Nanjing 210029, China;
3. Reservoir Dispatching Center of Hanjiang Water Conservancy and Hydropower Co., Ltd., Wuhan 430048, China
 2018
2018 
