2. 河海大学 理学院,江苏 南京 210098
河工模型试验中尾门控制用于调节模型边界流态与原型流态的相似,是开展模型试验的必备过程。非恒定流试验中需要实时调整尾门确保边界水位过程与天然相似。然而,人工尾门调节方式难以满足水位控制精度及连续性试验要求,因而,逐渐发展了尾门的自动控制系统。杨铁笙等[1-3]运用微机控制技术开发了河工模型尾门控制系统,虞邦义等[4]研发了差动式尾门控制系统,实现了对尾门的自动控制。水位变化比较复杂时,常规尾门控制系统控制精度难以满足规范要求。大量研究者引入PID等控制模型提高尾门控制系统的响应速度及控制精度。蔡辉等[5-6]根据水位变化特点,利用PID优化控制过程,提高了尾门水位控制系统的动态特性;李俊敏[7]运用伺服电机和推拉式尾门,采用PID调节算法,结合拉格朗日插值方法,实现了尾门水位的自动控制。杜剑锋等[8]采用分时PID控制,试验初始阶段停止PID控制,模型水位接近目标水位后再自动转入PID控制,解决了长江防洪模型目标水位降幅较大时尾门超调难题;然而,该控制方法针对特定模型,通用性能差。李晓飚等[9]运用模糊控制改进了水工模型尾门控制器,通过模糊控制器判断水位偏差分别选取比例或比例积分控制,提高了水位控制精度。
上述应用表明,PID控制模型有利于提高尾门控制精度,但难以解决水位速涨速落等复杂控制中超调或滞调等难题。虽然PID控制是最经典的反馈控制模型,具有很好的适应性和鲁棒性,但其控制效果与参数设置密切相关。常规尾门控制系统在试验过程中PID参数保持不变,降低了尾门控制系统的适应性,无法满足规范要求。自动控制领域内,通过模式识别判别控制偏差,实时整定PID参数,其控制效果明显更优[10-13]。因此,本文根据非恒定流试验过程中目标水位、水位跟踪偏差、水位预期变化趋势等特征,实时整定PID参数,提高控制系统动态响应特性,实现水位速涨速落等复杂情况的精确控制。
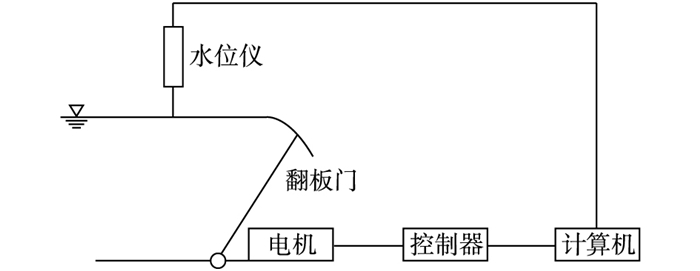
1 尾门控制系统设计常用尾门型式有翻板门和推拉门,推拉门存在止水困难、出流不稳、易受杂物阻挡等缺点,而翻板门具有动作灵活、出流稳定等优点。因此,选取翻板门作为尾门控制系统水位调节装置。系统主要包括水位仪、翻板门、电机、控制器和计算机(如图 1所示),计算机设定控制器参数,调节电机转速和方向,驱动翻板门变化,实现尾门水位的控制。
|
图 1 尾门控制系统结构 Figure 1 Structure of the tailgate control system |
水位仪实时测量水位H1(t),与目标水位H0(t)对比,得到水位偏差eH(t):
| $ {e_H}\left( t \right) = {H_1}\left( t \right) - {H_0}\left( t \right) $ | (1) |
水位偏差大于设定阈值,电机动作,重复迭代完成目标水位跟踪控制。电机转速PID控制模型为:
| $ u\left( t \right) = {k_{\rm{p}}}[e\left( t \right) + \frac{1}{{{T_{\rm{I}}}}}\int\limits_0^t {e\left( t \right){\rm{d}}t + {T_{\rm{D}}}\frac{{{\rm{d}}e\left( t \right)}}{{{\rm{d}}t}}}] $ | (2) |
kp,TI,TD分别为比例、积分、微分系数,e(t)为转速偏差,通过改变kp,TI,TD数值,控制电机运动速度和方向。kp较大提高电机转速,使翻板门快速动作加快水位调节,但过大kp易导致尾门水位出现超调和滞后。TI可消除系统累计偏差,促进系统逼近目标输出。TD根据偏差变化趋势产生超前控制,具有预见性。
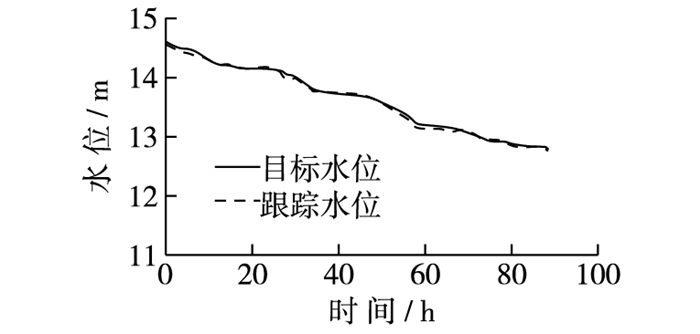
2 PID参数整定 2.1 固定PID参数试验PID参数主要通过理论计算、经验凑试或试验确定,实际中难以用数学模型或传递函数准确描述时,多采用经验凑试或试验确定,遵循“先比例、再积分、后微分”原则。以平原河流河工模型为例,控制目标水位变化较平缓(图 2),尾门控制选用PI控制模型,经验凑试kp为1.3,TI为3 s,尾门水位控制效果如图 2所示,最大跟踪误差小于1 mm。
|
图 2 水位跟踪过程 Figure 2 Water level tracking process |
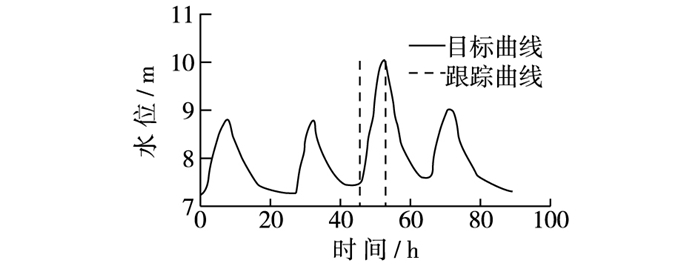
山区河流洪水过程中水位速涨速落,图 3是某山区河流洪水过程水位监测曲线,其中从45.5至53.5 h,8 h内水位涨幅达2.55 m。
|
图 3 山区河流水位变化过程 Figure 3 Hydrograph of water level changing in mountain rivers |
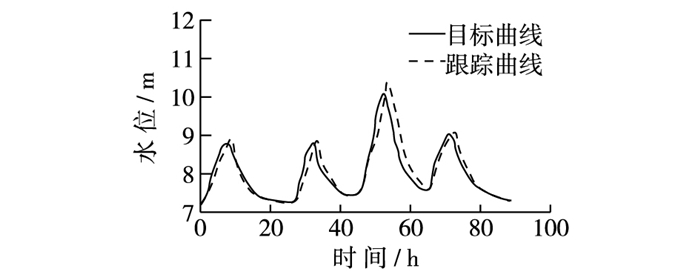
固定PID参数,尾门水位控制出现较大偏差(如图 4所示),增大kp,尾门水位出现超调;反之,又出现滞后。固定参数模式下,水位跟踪最大偏差达到1.3 mm,超出了规范要求。
|
图 4 常规PID参数整定跟踪过程 Figure 4 Process of tracking PID parameters self-tuning conventionally |
PID参数应与水位跟踪偏差、水位涨落速度、涨落预期以及跟踪相位等特征密切相关,根据实际控制经验运用产生式表示法总结尾门水位控制知识,形成专家知识库。产生式知识表示法是1943年E.Post根据串替规则提出的一种计算模型,其中每一条规则称为一个产生式。产生式用于表示因果关系知识,其基本形式为:IF a THEN b。a为前提,b为结论。
水位调节过程中,需要以水位跟踪偏差、水位涨落速度、涨落预期以及跟踪相位作为条件,调节电机动作。主要知识可表示为:
知识1,IF模型水位涨速大于原型水位涨速,THEN减小kp;
知识2,IF模型水位涨速小于原型水位涨速,THEN增大kp;
知识3,IF模型水位涨速等于原型水位涨速,THENkp不变;
知识4,IF模型水位降速大于原型水位涨速,THEN减小kp;
知识5,IF模型水位降速小于原型水位涨速,THEN增大kp;
知识6,IF模型水位降速等于原型水位涨速,THENkp不变;
知识7,IF模型水位预期上涨幅度超过原型水位,THEN减小TI;
知识8,IF模型水位预期上涨幅度小于原型水位,THEN增大TI;
知识9,IF模型水位预期上涨幅度等于原型水位,THENTI不变;
知识10,IF模型水位跟踪相位滞后,THEN增大TD;
知识11,IF模型水位跟踪相位超前,THEN减小TD;
知识12,IF模型水位跟踪相位相等, THEN TD不变。
尾门控制中,实时监测水位涨落速度、涨落趋势以及目标相位,对比知识库,做出相应调节。实时水位Hs(t)与目标水位Hm(t)的偏差ΔH(t):
| $ \Delta H\left( t \right) = {H_{\rm{s}}}\left( t \right) - {H_{\rm{m}}}\left( t \right) $ | (3) |
设实时水位Hs(t)与目标水位Hm(t)的变化率分别为H′(t)和H′m(t), 则
| $ H\prime \left( t \right) = {H_{\rm{s}}}\left( t \right) - {H_{\rm{s}}}\left( {t - 1} \right) $ | (4) |
| $ {H_{\rm{m}}}\left( t \right) = {H_{\rm{m}}}\left( t \right) - {H_{\rm{m}}}\left( {t - 1} \right) $ | (5) |
按照当前PID参数进行控制,水位理论上升时间为tHm,实际已上升时间为ts,则水位还将上升时间Δt为:
| $ \Delta t = {t_{H{\rm{m}}}} - {t_{\rm{s}}} $ | (6) |
| $ {\rm{设迭代因子}}\sigma :\sigma = \Delta tH\prime \left( t \right)/\Delta H\left( t \right) $ | (7) |
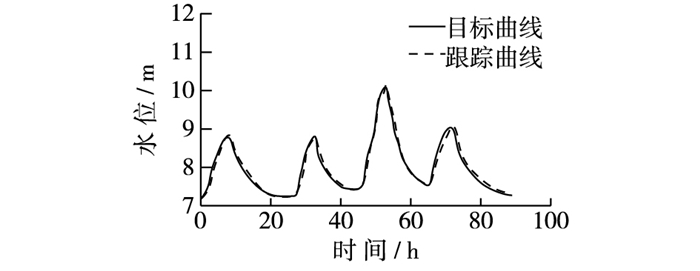
根据专家知识库,尾门控制策略为:σ < 1,则增大kp和TD;σ=1,kp和TD不变;σ>1,减小kp和TD;H′(t)>H′m(t),减小TI;H′(t) < H′m(t),增大TI;H′(t)=H′m(t),TI不变;接近水位最高点或最低点时,提前停止电机动作,依靠水位上升或下降惯性实现水位跟踪。kp,TI,TD具体调节幅度依据实际现场调节经验确定。图 5为PID参数自整定模式下水位控制过程,控制最大偏差仅为0.05 mm,相对于固定PID参数控制系统,自整定系统控制精度及动态响应性能大幅提高。
|
图 5 专家系统PID参数整定跟踪过程 Figure 5 Process of tracking PID parameters by self-tuning with expert system |
尾门自动控制对于非恒定流试验顺利开展至关重要,虽然PID控制器能够优化尾门控制性能,但仍然难以满足水位速涨速落等复杂条件下水位跟踪控制需求。为提高复杂条件下翻板门控制精度,以山区河流洪水过程为例。首先,运用固定PID参数模式实施了尾门控制,试验结果为水位控制最大偏差达到1.3 mm,超出了规范要求。然后,运用产生式学习法总结尾门控制系统PID参数调节规则,构建以水位跟踪偏差、水位涨落速度、涨落预期以及跟踪相位为关键要素的知识库,确立了12条控制策略,尾门控制时根据实测数据与知识库规则自主选择对应控制策略,实现PID参数的自整定。PID参数自整定大幅降低了水位控制偏差,同样山区河流水位控制,水位跟踪最大偏差仅为0.5 mm,尾门控制精度大幅提高。
本文仅讨论了单一尾门控制情况,多个尾门控制存在水位调整滞后,PID参数自整定方法及实施方案还有待改进完善。同时,非恒定流控制包括上边界流量控制,试验效果还需要考虑上边界流量控制精度。
| [1] |
杨铁笙, 安凤玲, 詹秀玲. 模型尾门水位控制方法研究[J]. 泥沙研究, 1993(1): 21-29. ( YANG Tiesheng, AN Fengling, ZHAN Xiuling. On the method for control of tailgate water level of a hydraulic model[J]. Journal of Sediment Research, 1993(1): 21-29. (in Chinese)) |
| [2] |
王昕, 蔡守允, 张河. 河工模型试验计算机测控系统[J]. 水利水电技术, 2003, 34(5): 57-59. ( WANG Xin, CAI Shouyun, ZHANG He. Computer control and measurement system for hydraulic model test[J]. Water Resources and Hydropower Engineering, 2003, 34(5): 57-59. (in Chinese)) |
| [3] |
贺昌海, 雷川华, 周小平, 等. 模型试验流量与水位自动控制系统研制[J]. 长江科学院院报, 2007, 24(3): 72-74. ( HE Changhai, LEI Chuanhua, ZHOU Xiaoping, et al. Research and development of automatic control system of discharge and water-level in model-testing[J]. Journal of Yangtze River Scientific Research Institute, 2007, 24(3): 72-74. (in Chinese)) |
| [4] |
虞邦义, 马浩, 俞国青. 差动式尾水调节系统数学模型[J]. 泥沙研究, 2005(1): 21-25. ( YU Bangyi, MA Hao, YU Guoqing. Mathematic model for difference-type tail-water measuring and controlling system[J]. Journal of Sediment Research, 2005(1): 21-25. (in Chinese)) |
| [5] |
蔡辉, 马洪蛟, 孙典红, 等. 水工模型水位的自动控制优化算法[J]. 河海大学学报(自然科学版), 2002, 30(5): 95-97. ( CAI Hui, MA Hongjiao, SUN Dianhong, et al. Optimized algorithm for automatic control of water level in hydraulic model experiments[J]. Journal of Hohai University(Natural Sciences), 2002, 30(5): 95-97. (in Chinese)) |
| [6] |
苏杭丽, 马洪蛟, 张东生, 等. 复合模型系统的控制策略[J]. 海洋工程, 2002, 20(2): 96-99. ( SU Hangli, MA Hongjiao, ZHANG Dongsheng, et al. Control strategies of hybrid model system[J]. The Ocean Engineering, 2002, 20(2): 96-99. (in Chinese)) |
| [7] |
李俊敏. 河工模型尾门水位控制系统的设计与研究[J]. 长江科学院院报, 2016, 33(5): 135-138. ( LI Junmin. Design and research of tail gate control system for river model experiment[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(5): 135-138. DOI:10.11988/ckyyb.20150107 (in Chinese)) |
| [8] |
杜剑锋, 马志敏, 范北林. 河工模型试验目标水位突降时尾门水位的控制[J]. 长江科学院院报, 2016, 33(4): 131-134. ( DU Jianfeng, MA Zhimin, FAN Beilin. A method of controlling water level at tail gate when target water level drops sharply in river model experiment[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(4): 131-134. DOI:10.11988/ckyyb.20150226 (in Chinese)) |
| [9] |
李晓飚, 赵国昌, 汪拥赤. P-FUZZY-PI控制器在水工模型水位控制系统中的应用[J]. 计算机测量与控制, 2005, 13(4): 341-343. ( LI Xiaobiao, ZHAO Guochang, WANG Yongchi. Application of P-FUZZY-PI controller in water level control system of hydraulic model experiments[J]. Computer Measurement and Control, 2005, 13(4): 341-343. (in Chinese)) |
| [10] |
HANG C C, ASTROM K J, HO W K. Refinements of the Ziegler-Nichols tuning formula[J]. Control Theory and Applications, 1991, 140: 143-162. |
| [11] |
孟祥泉. PID参数自整定方法研究与控制器研制[D]. 大连: 大连理工大学, 2010. (MENG Xiangquan. Research on the methods of PID parameters self-tuning and development of the controller[D]. Dalian: Dalian University of Technology, 2010. (in Chinese))
|
| [12] |
HE S Z, TAN S H, XU F L, et al. Fuzzy self-tuning of PID controllers[J]. Fuzzy Sets and Systems, 1993, 56(1): 37-46. DOI:10.1016/0165-0114(93)90183-I |
| [13] |
张永浩. 模糊PID自整定控制器的仿真研究[J]. 航海工程, 2005(5): 1-4. ( ZHANG Yonghao. The simulation study of PID-controllers with fuzzy self-adjusting parameter[J]. Ship and Ocean Engineering, 2005(5): 1-4. (in Chinese)) |
2. College of Science, Hohai University, Nanjing 210098, China
 2018
2018 