2. 南京理工大学,江苏 南京 210094
为了准确模拟天然河流的泥沙运动,必须随时测定模型试验水体的含沙量,其测量精度直接影响试验结果的准确性。根据测量原理的不同,含沙量测量仪分为直接测量法和间接测量法。直接测量方法有比重法与烘干法,这两种方法测量结果准确,但是费时费力,不能实时测量模型试验含沙量动态变化过程。间接测量法有光电式、同位素法及超声波和电容法等[1]。王娅娜等[2]研制的红外含沙量测量仪及马志敏等[3]研制的基于B超成像技术的含沙量测量仪,具有实时在线监测的功能,但是含沙量测量范围较低,只适用于体积浓度小于4‰以下(质量浓度约10 kg/m3以下)的低含沙量测量。雷廷武等[4]研制的近红外反射高含量泥沙传感器,泥沙测量范围可达300 kg/m3,但在低浓度(10 kg/m3以下)时,测量误差较大,传感器测量精度较低。针对河工、港工模型试验的特殊性,本研究依托国家重大科学仪器设备开发专项“我国大型河工模型试验智能测控系统开发”项目,开发出具有自主知识产权并适用于中国国情的成套水动力及泥沙关键参数量测仪器和量测技术[5-6],有助于提升大型河工模型试验研究水平。
1 光电含沙量测量仪基本原理水中含沙量大小与浊度虽无直接关系,但当水中有悬浮沙粒存在时,水的浊度会增加。含沙量不同时,水的浑浊程度也不同,因此可以通过光电测量法来测量含沙量的大小。光电测量法可分为透射测量法、散射测量法、透射散射比较法等[7],基本原理见图 1。
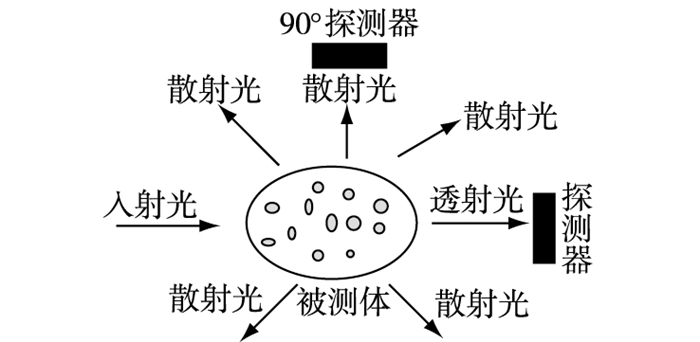
|
图 1 光电含沙量测量仪基本测量原理 Figure 1 Basic measuring principle of photoelectric sediment concentration instrument |
透射光式测量方法利用光电器件检测透射光强度。透射光强度随含沙量的变化遵循朗伯比尔(Lambert-Beer)定律,即透射光随含沙量增加按指数形式衰减:
| $ {I_{{\rm{trans}}}} = g{I_{{\rm{src}}}}{\rm{exp}}( - KL{S_{{\rm{trans}}}}) $ | (1) |
式中:Itrans是含沙量为Strans时的透射光强度; Isrc为入射光强度; K为比例常数; L为光源与光电接收器有效距离; g为测量仪器有关的几何参数; S为含沙量。设清水条件下测得的接收光强度为I0。
| $ 根据上式计算得:g = {I_0}/{I_{{\rm{src}}}} $ | (2) |
联立式(1),(2)得,透射含沙量Strans计算式如下:
| $ {S_{{\rm{trans}}}} = 1/(KL{\rm{ln}}({I_0}/{I_{{\rm{trans}}}})) $ | (3) |
散射光测量法利用水中悬浮颗粒对光的散射定理,当悬浮颗粒的直径远小于入射光波长时,散射规律可以用瑞利公式描述,散射光强与入射光的波长、悬浮颗粒体积、散射光与入射光的夹角有关。当悬浮颗粒直径大于入射光波长,各个方向的散射光强基本相等,用Mie定律[8]描述,若颗粒大小一致,可得到以下关系:
| $ {S_{{\rm{Msact}}}} = f({I_{{\rm{Msact}}}}) $ | (4) |
式中:IMscat为散射光强度; SMsact为散射光强为IMscat时的含沙量值。根据光电检测器件的位置不同,散射式浊度测量法可分为垂直散射式(90°散射)、前向散射式和后像散射式。因90°散射光强度对悬浮颗粒直径的变化最不敏感,而且受非散射途径的光影响最小,因此应用较广。
1.3 透射散射比较式测量法透射散射比较式测量法,又叫几分球式测量法,是同时测量透射光强度和散射光强度,再根据这两种光强度比值测定含沙量大小,即:
| $ S = f({I_{{\rm{Msact}}}}/{I_{{\rm{trans}}}}) $ | (5) |
透射散射比较式测量法是透射式和散射式两种测量方法的结合。仪器设计时要求,透射和散射光的测定光程相同,这样可以最大程度地消除水的色度和光源变化对测量结果的影响,但是这种方法线性度较差。
2 相对误差及不确定度试验测试中,误差是不可避免的。误差是测定值Xi与真值μ之差,分为绝对误差E和相对误差Er,E=Xi-μ,相对误差表示占真值的百分率,Er=(Xi-μ)/μ,相对误差更能反映测量的可信度。
不确定度[9-11]定义为表征合理地赋予被测量之值的分散性,与测量结果相关联的参数。这种测量不确定度的定义:Y=y±U,Y为被测量值,y为被测量值的估计值,U为测量不确定度。这表明,不确定度越小,所属结果与被测量的真值愈接近,其使用价值愈高。不确定度受被测量定义、测量装置或仪器的分辨率、测量人员技术水平、测量环境、随即因素等影响。不确定度分为A类与B类,A类不确定度的评定指用统计的方法,即用有限次测量数据的标准差估值来度量测量结果的不确定度分量uA; B类不确定度指用非统计方法,如仪器说明书、精确度等级、环境等因素计算出来的不确定度分量uB。为研究新研制含沙量设备的不确定度,本项目通过A类不确定度的分析方法获得含沙量测量仪的不确定度。
A类标准不确定度评定的表达式为uA=s(x),s(x)为标准差。其求法具体步骤如下:对被测量X进行多次测量,得测值x1, x2, …, xn(1, 2, …, n表示重复测量次数); 求算术平均值x和剩余误差vi=xi-x; 利用贝塞尔公式求标准差的估值:
为了研究透射光、散射光与含沙量之间的内在关系,本项目研制了一款无线含沙量测量仪,该含沙量测量仪由光电检测模块、数据采集模块、无线网络传输及存储等模块组成,能实现含沙量的实时在线测量与存储。含沙量测量仪结构框图和光电模块工作原理见图 2和3。
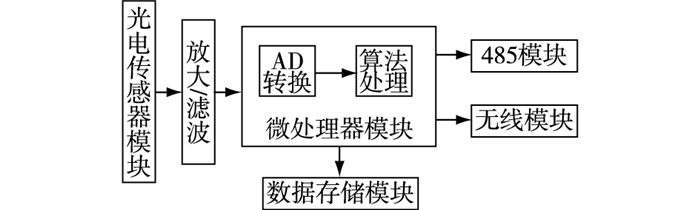
|
图 2 含沙量测量仪结构框图 Figure 2 Structure diagram of sediment concentration measuring instrument |
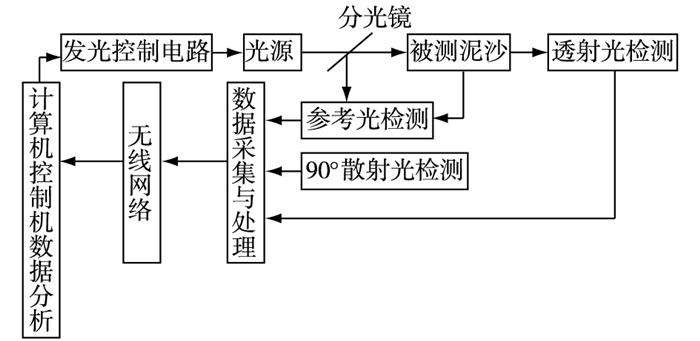
|
图 3 光电模块工作原理 Figure 3 Working principle of the photovoltaic module |
含沙量测量的光电检测模块采用多路分光技术,保证含沙量不受外界环境光影响。光电检测模块由分光镜、透射光检测、90°散射检测等组成。光源经分光镜分成两路相同光源,一路直接进入光电转换模块作为参考光源,另一路经过被测泥沙吸收、透射,散射等作用后,使用光电探测器将检测到透射光和90°散射光转换成电压信号并及时送入数据采集与处理模块。
4 试验研究及算法实现以河工模型试验常用的橙色塑料沙(粒径0.2 mm, 相对密度约1.02)为研究样本, 研究含沙量与透射光、散射光之间的内在关系。试验时采用标准100 mL的量筒准确量取1 000 mL的清水倒入烧杯中,用电子天平(分辨率0.01 g)分别称取沙样,配制标准体积浓度(Sv)的水沙混合液体,并确保搅拌均匀后放入含沙量测杆,上位机实时读取含沙量测量值。本文借助于MATLAB[12]软件的Curve Fitting回归分析、处理试验数据。
4.1 透射光与含沙量测试含沙量与透射光强的关系见表 1。
| 表 1 透射光强与含沙量测试数据 Table 1 Test data of transmission light intensity and sediment concentration |
通过表 1可以看出,含沙量低于9.71‰时,随着含沙量升高,透射光强Itrans值衰减变化非常小。含沙量在9.71‰与55.56‰时,随着含沙量的增加,透射光强Itrans衰减迅速。含沙量高于55.56‰时,透射光强Itrans随着含沙量的增加,衰减变化较小,含沙量测量范围趋于饱和。
如图 4所示,在全量程范围内,含沙量Sv与ln(I0/Itrans)在全量程范围内为一元非线性回归关系,但在9.71‰~72.73‰范围内,含沙量Sv与ln(I0/Itrans)呈线性变化,0~9.71‰范围内,也可以视作含沙量Sv与ln(I0/Itrans)呈线性关系。建立含沙量与测量均值的曲线方程,获得含沙量Sv与ln(I0/Itrans)之间的关系如下:
| $ {S_{\rm{v}}} = \left\{ \begin{array}{l} 98.67{\rm{ln}}({I_0}/{I_{{\rm{trans}}}}) + 0.58\;\;\;\left( {{\rm{ln}}\left( {{I_0}/{I_{{\rm{trans}}}}} \right) \le 0.25} \right)\\ 19.38{\rm{ln}}({I_0}/{I_{{\rm{trans}}}}) + 10.05\;\;\;\;\;(0.25<{\rm{ln}}({I_0}/{I_{{\rm{trans}}}}) \le 3.3) \end{array} \right. $ |
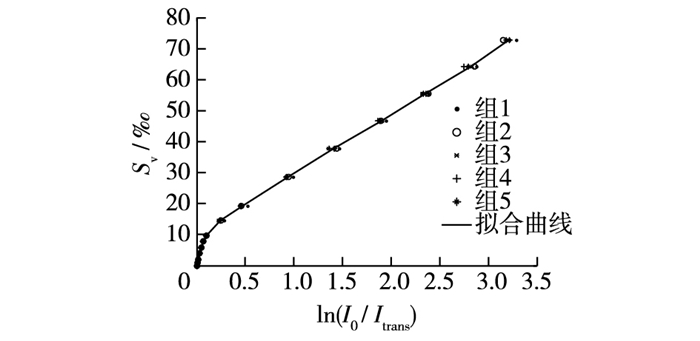
|
图 4 含沙量Sv与ln(I0/Itrans)曲线关系 Figure 4 Relationship curves between sediment concentration Sv and ln( I0/Itrans) |
计算测量均值ln(I0/Itrans)所求得的含沙量值与实际含沙量之间的相对误差,结果如表 2所示。
| 表 2 含沙量测量均值相对误差 Table 2 Relative errors of mean sediment concentration |
由表 2可知,在0~9.71‰范围内,使用透射法测量含沙量,测量结果的相对误差较大,测量精度不高。因此需提高此范围内的含沙量测量精度。
4.2 透射光功率影响由于测沙仪的比例常数K和光源与光电接收器有效距离L均为固定值,通过增强和降低光源的工作功率,研究入射光强对含沙量率定曲线及相对误差的影响,测量结果如表 3所示(表中光源1的光功率大于光源2的光功率)。
| 表 3 不同透射光强与含沙量测试数据 Table 3 Test data of different transmission light intensity and sediment test concentration |
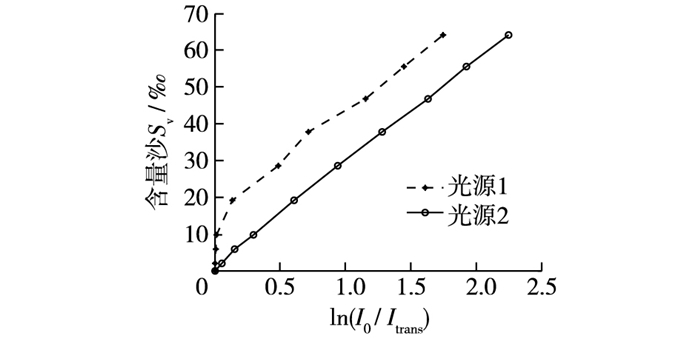
如表 3所示,含沙量较低时(0<Sv≤9.71‰),光源1的透射光强Itrans衰减程度远低于光源2的透射光强Itrans,而含沙量较高时(Sv≥55.56‰),光源2的透射光强Itrans衰减基本结束,而光强1的透射光强Itran可一直衰减至Sv=81.08‰。并由图 5可知,光源2的In(I0/Itrans)与含沙量Sv在全量程范围内为一元线性回归关系。因此可推得,提高光源光功率可以提高含沙量测量范围,但在低浓度范围内,测试准确度较低; 降低光源光功率可以改善含沙量Sv与In(I0/Itrans)之间的线性关系,但含沙量测量范围相对变小。
|
图 5 含沙量与光源功率变化曲线 Figure 5 Relationships between sediment concentration and light source power |
从表 3还可以看出,光源2条件下测量含沙量,在含沙量Sv≤5.85‰时,测量误差仍然较大,因此本研究考虑引入90°散射法测量低浓度的含沙量。
4.3 90°散射与含沙量测试由表 4可知,90°散射光检测值随含沙量的增加而变大,并逐渐趋于饱和。使用Matlab的Curve Fitting,将0~12.11‰内的5组数据做算术均值处理,得到含沙量S与散射均值光强的拟合方程Sv=0.001 52 IMsact2+0.142 6IMsact-0.769。计算90°散射检测均值的相对误差,结果如表 5所示。
| 表 4 90°散射光强与含沙量测试数据 Table 4 Test data of 90°scattered light and sediment concentration |
| 表 5 90°散射光与含沙量测试数据均值相对误差 Table 5 Test data mean relative errors of 90°scattered light and sediment concentration |
由表 2和表 5对比可见,0~12.11‰含沙量时,采用90°散射法检测含沙量,检测结果的相对误差比透射法检测要小。因此,采用90°散射法与透射法相结合的测沙方法,既确保含沙量测量范围,又确保低浓度含沙量的测量准确度。
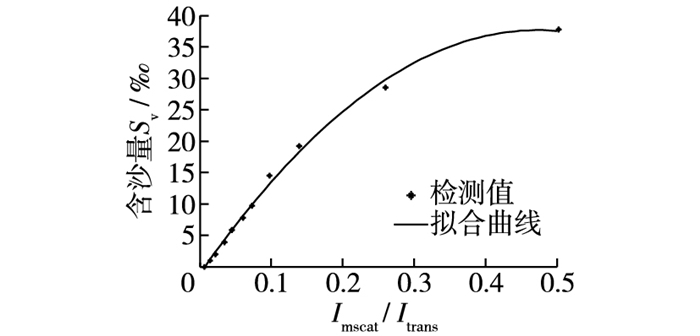
4.4 透射散射比较式与含沙量测试选用表 4及表 1中均值IMsact,构建S=f(IMsact/Itrans)的曲线关系,如图 6所示。从图 6可知,采用透射散射比较式测量含沙量,含沙量Sv与IMsact/Itrans为一元非线性回归关系,含沙量达28.57‰时,测量已趋于饱和,因此,采用透射散射比较式方法,含沙量测量范围较小。
|
图 6 含沙量Sv与IMsact/Itrans曲线关系 Figure 6 Relationship curve between sediment concentration Sv and IMsact/Itrans |
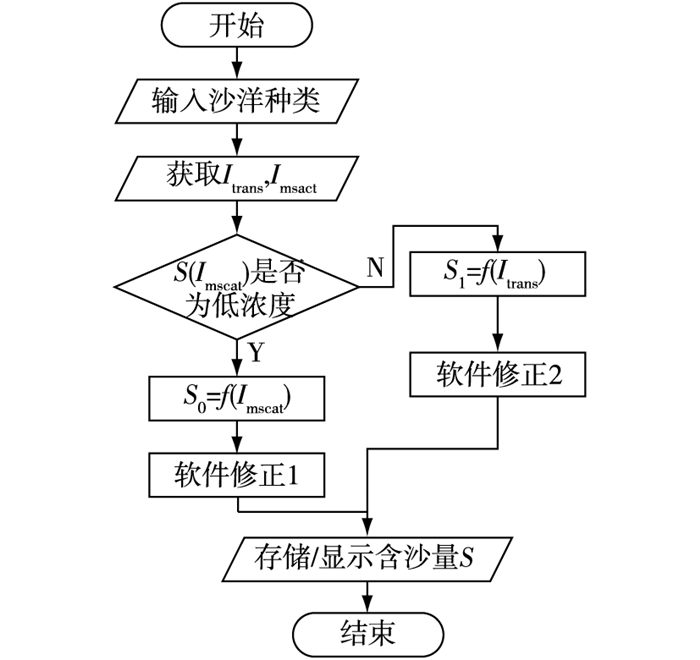
研究设计的含沙量测量仪的数据处理主要分为硬件的预处理与上位机软件处理与分析两部分。硬件预处理主要将采集到的透射光、散射光信号与参考光源信号进行比较计算,消除环境光和暗电流对测试的影响。上位机首先预设定测量沙样的种类,然后对含沙量的浓度做预先判断,若属于低浓度范围,则采用散射法测量并作补偿等修正,若不属于低浓度范围,则采用透射法测量并作补偿等修正,最后存储并显示测沙结果。具体流程见图 7。
|
图 7 含沙量算法流程 Figure 7 Flow chart of sediment concentration algorithm |
为进一步衡量含沙量测量系统的误差,用不确定度进行分析。具体方法为,使用测沙仪多次测量相同浓度的水沙混合液体,测量结果如表 6所示,使用A类不确定度分析方法进行分析,得到测沙仪各测点的不确定度。由于试验为同一测试人员在相同条件下测试,因此无其他不确定度分量,计算可得测沙仪各测点的不确定度,计算结果如表 6所示。
| 表 6 含沙量测试及各测点不确定度 Table 6 Measurement of sediment concentration and uncertainty of each measuring point |
由表 6可知,所研制的含沙量测量仪测量橙色塑料沙(粒径约0.2 mm, 相对宽度约1.02)样本,其测量范围为0~64.22‰(质量浓度为0~70 kg/m3),在测量范围内,各测点的相对误差均小于5%,相对不确定度均小于0.4。
为验证新研制的含沙量测量仪对不同粒径及其他种类的沙样具有相同适应性,将此仪器在水利部水文仪器及岩土工程仪器治疗监督检测中心做第三方检测,相关测试数据表明,该含沙量测量仪测试粒径约为0.075和0.11 mm,相对密度约为1.02的模型沙,粒径约为0.2 mm的木屑粉及粒径约为0.05 mm江沙,其测量范围均可达0~64.22‰(质量浓度为0~70 kg/m3)。在测量范围内,各测点的相对误差均小于5%,重复性误差小于5%,各测点的不确定度如表 7所示。从表 7可知,测量仪在测量表中所列沙样模型,在测量范围内,其不确定度均小于0.3。与现有文献[2-4]中研制的含沙量仪器相比,该测量仪在测量低含沙量时可获得较高的测量精度,同时具有较宽的测量范围,且不确定度较小,仪器性能稳定。
| 表 7 含沙量不确定度分析 Table 7 Uncertainty analysis of sediment concentration tests |
首先阐述了光电含沙量测量仪的基本原理及常用方法,并介绍新研制的一套无线含沙量测量仪的基本组成。通过透射法、散射法、透射散射比较法,调节光功率等试验研究,确定含沙量测量仪采用透射法与散射法组合的方式测量,并采用不确定度分析方法,分析新研制的测量仪的可靠性。试验表明,新研制的含沙量测量仪,测量模型试验常用的橙色塑料沙(粒径约0.075,0.11和0.20 mm, 相对密度约1.02),木屑粉(粒径约0.075 mm)及江沙(粒径约0.05 mm)测量范围为0~64.22‰(质量浓度为0~70 kg/m3),仪器的不确定度小于0.4。本次研究目前采用的沙样种类及粒径种类较少,下一步将开展更多模型沙及更多粒径组的试验,以完善该含沙量测量方法。
| [1] |
蔡守允, 朱其俊, 张晓红. 模型试验含沙量测量仪器的分析研究[J]. 水资源与水工程学报, 2007, 18(5): 83-85. ( CAI Shouyun, ZHU Qijun, ZHANG Xiaohong. Study on the instruments of measuring sediment concentration in the model test[J]. Journal of Water Resources and Water Engineering, 2007, 18(5): 83-85. (in Chinese)) |
| [2] |
王娅娜, 蔡辉, 马洪蛟, 等. 红外实时测沙仪研制及其应用[J]. 海洋工程, 2007, 25(3): 132-135. ( WANG Ya'na, CAI Hui, MA Hongjiao, et al. Research on real-time wireless sediment measurement system and its application in annular flume[J]. The Ocean Engineering, 2007, 25(3): 132-135. (in Chinese)) |
| [3] |
马志敏, 邹先坚, 赵小红, 等. 基于B超成像的低含沙量测量[J]. 应用基础与工程科学学报, 2013, 21(4): 796-803. (MA Zhimin, ZOU Xiaohong, et al. The measurement of low sediment concentration based on B-Mode ultrasound images[J]. Journal of Basic Science and Engineering, 2013, 21(4): 796-803. (in Chinese))
|
| [4] |
雷廷武, 张宜清, 赵军, 等. 近红外反射高含量泥沙传感器研制[J]. 农业工程学报, 2013, 29(7): 51-57. ( LEI Tingwu, ZHANG Yiqing, ZHAO Jun, et al. Study on near infrared reflectance sensor for high sediment concentration measurement[J]. Transactions of the Chinses Society of Agricultural Engineering, 2013, 29(7): 51-57. (in Chinese)) |
| [5] |
夏云峰, 陈诚, 王驰, 等. 国家重大科学仪器专项"我国大型河工模型试验智能测控系统开发"研究进展: 水利量测技术论文选集(第九集)(C)//郑州: 黄河水利出版社, 2014. (XIA Yunfeng, CHEN Cheng, WANG Chi, et al. Advances in the national key scientific instrument and equipment development project "the development of intelligent measurement and control system for large-scale river model test in China": Selection of water resources measurement technology papers(Ninth episodes)[C]//Zhengzhou: Yellow River Water Conservancy Press, 2014. (in Chinese))
|
| [6] |
王驰, 黄海龙, 霍晓燕. 具有侧向补偿的激光无线高精度测沙仪: 水利量测技术论文选集(第九集)(C)//郑州: 黄河水利出版社, 2014. (WANG Chi, HUANG Hailong, HUO Xiaoyan. The adjustable laser wireless high-precision sand meter based on the lateral compensation: Selection of water resources measurement technology papers(Ninth episodes)//Zhengzhou: Yellow River Water Conservancy Press, 2014. (in Chinese))
|
| [7] |
盛强. 散射光式浊度仪及信号处理的研究[D]. 太原: 太原理工大学, 2007. (SHENG Qiang. The research of technology on scattering-light turbidimeter and signal processing[D]. Taiyuan: Taiyuan University of Technology, 2007. (in Chinese))
|
| [8] |
岳舜琳, 陈国光, 童俊, 等. 低浊水的浊度测定问题[J]. 净水技术, 2010, 29(3): 48-53. ( YUE Shunlin, CHEN Guoguang, TONG Jun, et al. Turbidity measurement for drinking water with low turbidity[J]. Water Purification Technology, 2010, 29(3): 48-53. (in Chinese)) |
| [9] |
JJF 1059-1999测量不确定度评定与表示[M]. 北京: 中国计量出版社, 1999. (JJF 1059-1999 The measurement uncertainty evaluation[M]. Beijing: China Metrology Press, 1999. (in Chinese))
|
| [10] |
刘庆, 邵志新. 回归分析的直线拟合不确定度探讨[J]. 中国测试技术, 2009, 35(3): 41-44. ( LIU Qing, SHAO Zhixin. Discussion of liner fitting uncertainty of regress analysis[J]. China Measurement and Test, 2009, 35(3): 41-44. (in Chinese)) |
| [11] |
蔡大川, 冉文清. 浊度计测量结果不确定度分析[J]. 中国测试技术, 2005, 31(3): 42-44. ( CAI Dachuan, RAN Wenqing. Uncertainty analysis of the relative indication error of turbidimeter[J]. China Measurement Technology, 2005, 31(3): 42-44. (in Chinese)) |
| [12] |
陈岚峰, 杨静瑜, 崔崧, 等. 基于MATLAB的最小二乘曲线拟合仿真研究[J]. 沈阳师范大学学报(自然科学版), 2014, 32(1): 75-79. ( CHEN Lanfeng, YANG Jingyu, CUI Song, et al. MATLAB simulation of curve fitting based on least-squares[J]. Journal of Shenyang Normal University(Natural Science Edition), 2014, 32(1): 75-79. (in Chinese)) |
2. Nanjing University of Science and Technology, Nanjing 210094, China
 2018
2018 