2. 三峡大学土木与建筑学院,湖北宜昌 443002
混凝土抗冻性不足是造成耐久性破坏的主要原因之一,高寒地区的混凝土构筑物不仅会遭受不同程度的冻融破坏,还会受到地震作用、波浪冲击、车辆碾压等循环荷载的作用。目前未遭受环境劣化混凝土的静动态力学性能的研究已经硕果累累,国内外学者基本达成共识[1-5],但国内关于冻融劣化混凝土静动态力学性能的研究于2000年左右才得到重视。Penttala等学者对冻融劣化混凝土的应力-应变关系和变形特性进行了试验研究,得到了应力、应变与冻融循环次数的表达式[6-7]。我国学者对冻融劣化混凝土的单轴抗压、抗折、抗拉强度以及变形特征、弹性模量等方面的研究结论基本达成一致[8-9],覃丽坤等[10-12]对冻融劣化混凝土进行了双轴压和双轴拉压的标准静态加载试验,分析了其基本力学特性并建立了相应的破坏准则,清华大学对混凝土在冻融过程中的变形、孔隙压力及温度分布进行了数值仿真[13]。随着理论研究的深入,有学者基于损伤力学和弹塑性理论建立了冻融劣化混凝土在不同应力状态下的损伤本构模型[14-15]。以上所述均是静态加载试验的研究成果,目前对于冻融劣化混凝土的动态试验研究和理论研究极少。因此,本文对冻融劣化混凝土单轴循环加卸载的外包络线及能量演化研究是对混凝土动态力学性能的重要补充,拟为高寒地区大坝、桥墩、海洋平台等水工混凝土构筑物的设计提供参考。
1 试验过程 1.1 试验设备试验设备主要有TR-TSDRSL冻融仪、10 MN大型多功能动静力三轴仪和声发射仪器。TR-TSDRSL冻融仪主要由控制系统、冻融箱和冷却塔组成,冻融液的冰点为-45 ℃,本试验混凝土试件的中心温度为(-17±2)℃~(8±2)℃,能够保证混凝土达到冻结所需温度冻融液不结冰,适用于普通混凝土快冻法。10 MN大型多功能动静力三轴仪主要由微机EDC控制系统、加载系统、主伺服油源、辅助伺服油源四大部分组成,能够用于常三轴和真三轴动静力加载试验,竖向最大动、静力加载值分别为5和10 MN,最大应变速率为10-2/s。声发射仪器能够对加载全过程进行无损探伤,评估损伤状态。
1.2 试件制备及养护考虑到混凝土的强度随尺寸增大而减小的特性[16],本文采用边长为300 mm的二级配C30混凝土立方体试件进行试验研究更符合工程实际。水泥采用P·C 32.5复合硅酸盐水泥,试验用砂为中砂,粗骨料为粒径5~40 mm的连续级配碎石,混凝土的配合比为水:水泥:砂:石子=0.46:1.00:1.45:3.38,中石和小石的比例为6:4。具体材料用量为:水175.0 kg/m3,水泥381.7 kg/m3,砂553.0 kg/m3,小石516.0 kg/m3,中石774.0 kg/m3。
试件采用钢模浇筑成型。为使小石、中石、砂、水泥充分搅拌均匀,先将这些材料放入搅拌机干拌3 min,然后加入称量好的自来水进行湿拌,时间不超过10 min。将搅拌好的混凝土置于钢模中,振捣密实,抹面,于自然环境中静置24 h后拆模,将编号后的试件放入养护室养护28 d后移至室外自然养护,控制养护室的相对湿度和温度分别为90%和(20±3)℃。
1.3 试验步骤试验分为以下3个步骤:
(1) 冻融循环处理:将试件置于装水的试件盒中浸泡12~14 d使其饱和,试件充分饱和后补充水至液面高出试件上表面约5 mm,安装温度传感器。准备就绪后控制冻融温度,进行冻融循环。结束后随机挑选4个试件,将试件表面清理干净后称重并记录。用砂浆对试件因冻融而剥落的地方进行抹平处理。抹平用砂为公称粒径为1.25 mm的细砂,砂浆配合比为砂子:水泥:水= 9.33:6.44:2.96。
(2) 试件安放及声发射安装和检查:将传力垫板置于试件受压面上,调整小车、垫板、传力柱和试件直至严格对中。安装竖向变形计和声发射装置并检测所有声发射信号通道。
(3) 加载试验:预加载时将辅助伺服油源油压调到5 MPa,当传力柱和试件上部垫板即将接触时采集声发射数据,继续加载到20 kN并持荷3 min后停止声发射数据采集;正式加载时按照等应变递增方式(每次Δε=0.002)进行单轴循环加卸载并采集声发射数据直到试件被完全破坏。
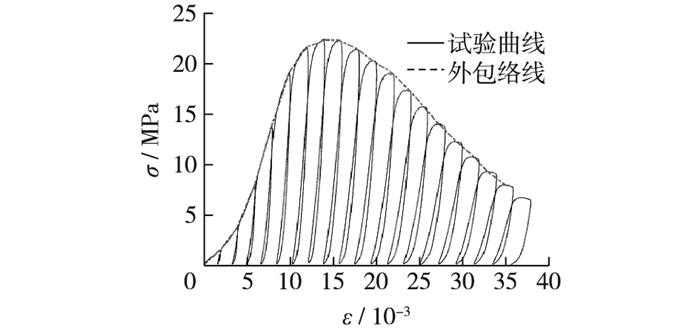
2 混凝土外包络线特征分析用一条曲线将应力-应变试验全曲线包络其中,这条曲线即为外包络线,如图 1为冻融循环35次的混凝土以应变速率为10-4/s进行单轴循环加卸载时的应力-应变曲线及其外包络线。图 2为历经不同冻融循环后在应变速率为10-4/s下的单轴循环加卸载试验的外包络曲线。图 3为冻融循环0次和50次后以不同应变速率循环加卸载得到的应力-应变全曲线包络线。
|
图 1 冻融循环35次,10-4/s时的应力-应变曲线及其包络线 Figure 1 Stress-strain curve and envelope curve for 35 times freeze-thaw under strain rate of 10-4/s |
|
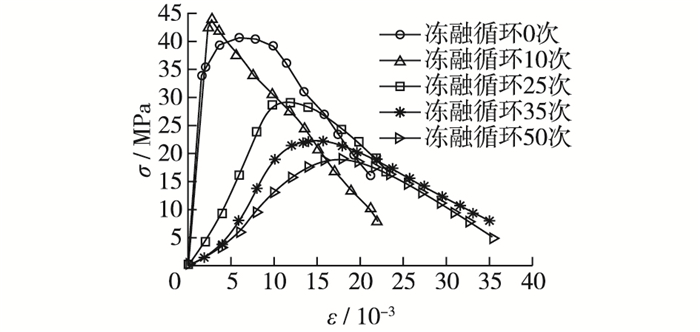
图 2 10-4/s时的应力-应变曲线包络线 Figure 2 Envelope curve of stress-strain curve under strain rate of 10-4/s |

|
图 3 冻融循环0次和50次的应力-应变曲线外包络线 Figure 3 Envelope curve of stress-strain curve for 0 and 50 times freeze-thaw specimen |
由图 2可知:①随着冻融循环次数的增加,外包络线上升段逐渐明显地分为直线段和曲线段,这是因为冻融循环使得混凝土内部孔隙率增大,循环加卸载的前期对混凝土有明显的压实作用;②冻融循环不超过10次时,应力-应变曲线外包络线与非冻融混凝土在单调加载时的应力-应变曲线形状基本相同,这是因为循环次数较少,混凝土内部的冻融损伤较小;③冻融循环超过10次后,上升段的拐点都在应变为0.005处波动,并且随着冻融循环次数的增多,上升段的平均斜率逐渐变小,即混凝土的弹性模量逐渐降低;④随着冻融循环次数的增多,混凝土的峰值应力逐渐减小而峰值应变逐渐增大,这是因为冻胀作用带来的损伤随着冻融循环次数的增多而增大,因而峰值应力减小,同时试件内部孔隙随着冻胀次数的增多而增加,引起体积增大,因而峰值应变略大于未冻融的混凝土。
对比图 3可知:①无论应变速率为多大,冻融循环50次后的外包络线上升段分为明显的直线段和曲线段,而未冻融的则基本呈直线上升;②未经冻融循环的混凝土的峰值应力随着应变速率的增大而逐渐增大,而冻融循环50次后混凝土的峰值应力随应变速率的增大呈现出先增大后减小的趋势,这说明冻融循环破坏了混凝土的内部结构,影响了混凝土的率敏感性。
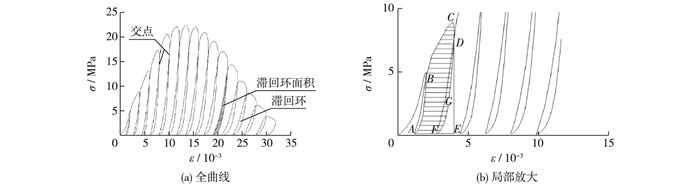
3 混凝土能量演化规律研究 3.1 循环加卸载下混凝土能量的定义本试验根据肖福坤[17]关于煤层循环加卸载试验中对能量定义进行了改进。按照等应变方式进行循环加卸载,得到冻融循环35次后以10-3/s进行循环加卸载的应力-应变试验全曲线,见图 4(a);并取局部放大图进行剖析,见图 4(b)。
|
图 4 应力-应变全曲线及局部放大 Figure 4 Stress-strain curve and partially enlarged drawing |
滞回环AB的面积代表耗散能,用ΦD表示,即
| $ {\mathit{\Phi} _{\rm{D}}} = \sum\limits_{i = 2}^n {\left( {\int_{{A_i}}^{{B_i}} {\sigma {\rm{d}}\varepsilon }-\int_{{B_{i-1}}}^{{A_{i-1}}} {\sigma {\rm{d}}\varepsilon } } \right)} $ | (1) |
式中:i为第i个加卸载过程;n为各试样所能承受的循环加缷载次数。
定义由卸载曲线与再加载曲线的交点至卸载为零的点这段曲线下方的面积(即图中DEFG所围成的面积)为弹性应变能,用ΦSE表示,即
| $ {\mathit{\Phi} _{{\rm{SE}}}} = \sum\limits_{i = 1}^n {\int_{{B_i}}^{{A_i}} {\sigma {\rm{d}}\varepsilon } } $ | (2) |
阴影部分面积为塑性应变能,用ΦSP表示,即
| $ {\mathit{\Phi} _{{\rm{SP}}}} = \sum\limits_{i = 2}^n {\left( {\int_{{A_i}}^{{D_i}} {\sigma {\rm{d}}\varepsilon }-\int_{{D_i}}^{Fi} {\sigma {\rm{d}}\varepsilon {\rm{-}}{\mathit{\Phi} _{{\rm{D}}, i}}} } \right)} $ | (3) |
式中:ΦD, i为前i个加载过程的耗散能。
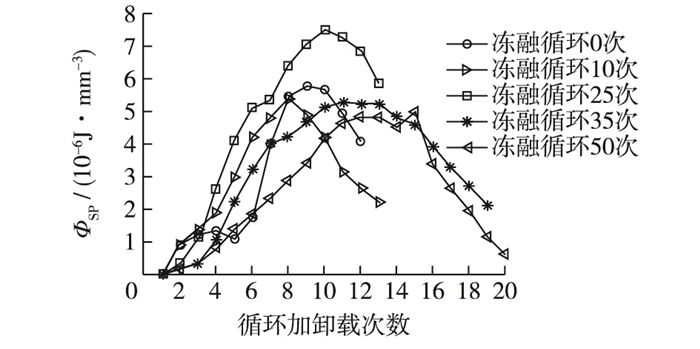
3.2 耗散能与循环加卸载次数的关系将10-4/s时的试验过程全曲线利用式(1)进行处理,得到耗散能与循环加卸载次数之间的关系,如图 5所示。由图 5可知:①冻融循环后,混凝土的耗散能随着循环次数的增加,整体上呈现先增加后减小的趋势,且曲线形状与混凝土单轴单调加载的应力-应变曲线相似;②冻融循环达到35次后的耗散能增加速度相对于冻融0次、10次、25次的明显减慢,耗散能的最大值也小于冻融0次、10次、25次的耗散能最大值;③前2~4次循环加卸载时耗散能增加缓慢,原因是这一阶段混凝土的微小裂缝被压实致密,随后耗散能增加速度加快,混凝土内部的微裂纹逐渐增加。
|
图 5 耗散能与循环加卸载次数的关系 Figure 5 Relationship between dissipated energy and loading-unloading cycles |
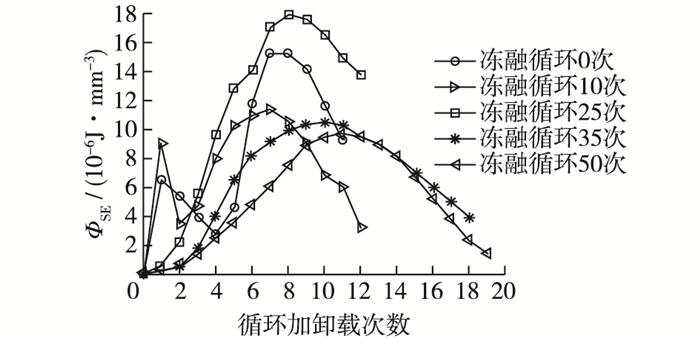
将10-4/s时的试验过程全曲线利用式(2)进行处理,得到弹性应变能与循环加卸载次数之间的关系,如图 6所示。由图 6可知:①应变速率为10-4/s时,混凝土的弹性应变能随着循环加卸载次数的增加整体上呈先增后减的变化趋势,其变化规律曲线和混凝土单轴循环加卸载压缩试验外包络曲线类似;②当冻融循环不超过10次时,循环加卸载初期,混凝土弹性应变能呈现出一定的波动。这主要是因为当冻融循环不超过10次时,混凝土的脆性较强,循环加卸载时容易发生剪压破坏;当冻融循环超过10次时,混凝土的脆性减弱,主要发生轴压破坏,如图 7所示。
|
图 6 弹性应变能与循环加卸载次数的关系 Figure 6 Relationship between elastic strain energy and loading-unloading cycles |

|
图 7 混凝土破坏形态 Figure 7 Failure form of concrete |
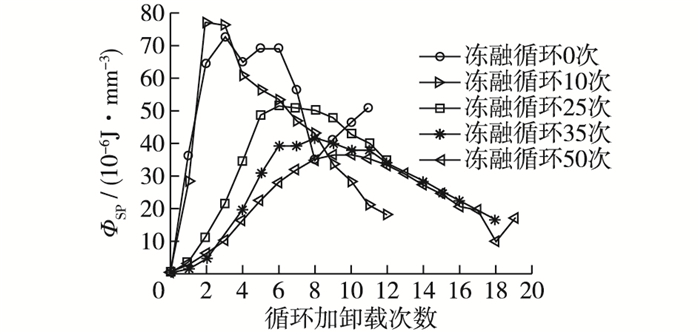
塑性应变能与循环加卸载次数的关系以10-4/s时的试验数据为例,利用式(3)进行处理。由图 8可知:①在相同应变速率下,混凝土塑性应变能随着循环加卸载次数的增加整体上呈先增后减的变化趋势;②混凝土破坏时循环加卸载的次数随着冻融循环次数的增加而增加,这说明冻融循环使得混凝土的脆性减弱。
|
图 8 塑性应变能与循环加卸载次数的关系 Figure 8 Relationship between plastic strain energy and loading-unloading cycles |
殷有泉认为材料的塑性变形与损伤同时出现,两者演化规律相互耦合[18]。根据能量损伤理论,材料的损伤被视为能量转换的不可逆过程。基于上述两点,将塑性应变能ΦSP和耗散能ΦD这两种不可逆的能量总和定义为混凝土的损伤能量ΦS,即定义:
| $ {\mathit{\Phi} _{\rm{S}}} = {\mathit{\Phi} _{{\rm{SP}}}} + {\mathit{\Phi} _{\rm{D}}} $ | (4) |
定义损伤变量为:
| $ D = {{\mathit{\Phi}} _{\rm{S}}}/{\mathit{\Phi}} $ | (5) |
式中:Φ为外力所做的功,即能量的总和。
将式(1)~(3)带入式(4)和(5)得:
| $ D = \left( {\sum\limits_{i = 2}^n {\left( {\int_{{A_i}}^{{D_i}} {\sigma {\rm{d}}\varepsilon }-\int_{{D_i}}^{Fi} {\sigma {\rm{d}}\varepsilon }-{\mathit{\Phi} _{{\rm{D, }}i}}} \right) + \sum\limits_{i = 2}^n {\left( {\int_{{A_i}}^{{B_i}} {\sigma {\rm{d}}\varepsilon }-\int_{{B_{i - 1}}}^{{A_{i - 1}}} {\sigma {\rm{d}}\varepsilon } } \right)} } } \right)/\sum\limits_{i = 1}^n {\int_{{A_i}}^{{F_i}} {\sigma {\rm{d}}\varepsilon } } $ | (6) |
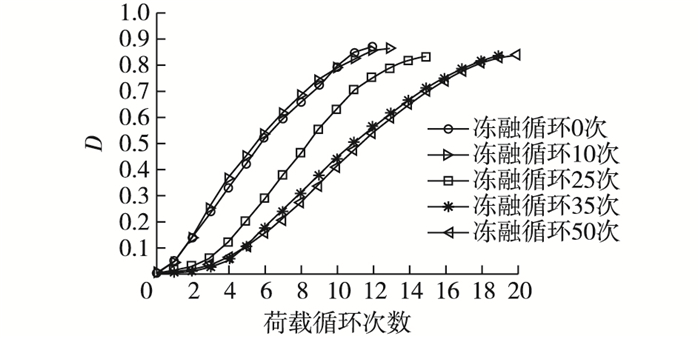
根据前文处理得到的3种能量数据,结合式(6)得到10-4/s时的损伤变量与循环加卸载次数的关系如图 9所示。分析可知:①损伤大致分为三阶段:损伤初始发展阶段、损伤快速发展阶段和损伤完全发展阶段;②冻融作用增加了混凝土的延性,这是因为在内部水的冻胀-融化过程中,混凝土的微观结构变松散,脆性减弱;③外力对混凝土做功,产生的90%的能量用于不可逆转的变化过程。
|
图 9 损伤变量曲线 Figure 9 Damage variable curve |
本试验对不同冻融循环次数、不同应变速率下的混凝土循环加卸载试验全曲线和外包络线的特性进行了研究,对耗散能、弹性应变能和塑性应变能进行了相关定义并分析了这3种能量与循环加卸载次数之间的关系,得到以下结论:
(1) 随着冻融循环次数的增加,外包络线上升段逐渐明显地分为直线上升段和曲线上升段,当冻融循环超过10次后,上升段的拐点都在应变为0.005处波动,曲线整体上呈先增后减的趋势。
(2) 随着冻融循环次数的增多,混凝土的峰值应力逐渐减小而峰值应变逐渐增大。
(3) 应变速率不影响应力-应变外包络线的形状;冻融循环影响混凝土的率敏感性。
(4) 混凝土的耗散能、弹性应变能和塑性应变能与循环加卸载次数之间的变化规律基本一致,整体上均随循环加卸载次数的增加呈先增大后减小的变化规律;冻融循环增强了混凝土的延性。
(5) 从能量角度分析,混凝土的损伤分为阶段,且外力做功的90%的能量用于塑像变形和损伤累积。
| [1] |
BURLION N, GATUINGT F, PIJAUDIER-CABOT G, et al. Compaction and tensile damage in concrete: Constitutive modeling and application to dynamics[J]. Computer Methods in Applied Mechanics Engineering, 2000, 183(3/4): 291-308. |
| [2] |
ASLANI F, JOWKARMEIMANDI R. Stress-strain model for concrete under cyclic loading[J]. Magazine of Concrete Research, 2012, 64(8): 673-685. DOI:10.1680/macr.11.00120 |
| [3] |
TEDESCO J W, POWELL J C, ROSS C A, et al. A strain-rate-dependent concrete material model for ADINA[J]. Computer & Structures, 1997, 64(5/6): 1053-1067. |
| [4] |
肖诗云, 张剑. 不同应变率下混凝土受压损伤试验研究[J]. 土木工程学报, 2010, 43(3): 40-45. ( XIAO Shiyun, ZHANG Jian. Compressive damage experiment of concrete at different strain rates[J]. China Civil Engineering Journal, 2010, 43(3): 40-45. (in Chinese)) |
| [5] |
王立成, 宋玉普. 混凝土双轴受压动态强度准则[J]. 水电能源科学, 2012, 30(1): 139-142. ( WANG Licheng, SONG Yupu. Dynamic strength criterion of concrete under biaxial compression[J]. Water Resources and Power, 2012, 30(1): 139-142. (in Chinese)) |
| [6] |
PENTTALA V, AL-NESHAWY F. Stress and strain state of concrete during freezing and thawing cycles[J]. Cement and Concrete Research, 2002, 32(9): 1407-1420. DOI:10.1016/S0008-8846(02)00785-8 |
| [7] |
HADSN M, UEDA T, SATO Y. Stress-strain relationship of frost-damaged concrete subjected to fatigue laoding[J]. Journal of Materials in Civil Engineering, 2008, 20(1): 37-45. DOI:10.1061/(ASCE)0899-1561(2008)20:1(37) |
| [8] |
刘学波, 宋玉普. 冻融循环后湿筛大骨料混凝土的试验研究[J]. 水电能源科学, 2009, 27(3): 97-99. ( LIU Xuebo, SONG Yupu. Experimental study on wet-screened mass concrete behavior after freeze-thaw cycles[J]. Water Resources and Power, 2009, 27(3): 97-99. (in Chinese)) |
| [9] |
曹大富, 富立志, 杨中伟, 等. 冻融循环作用下混凝土受压本构特征研究[J]. 建筑材料学报, 2013, 16(1): 17-23. ( CAO Dafu, FU Lizhi, YANG Zhongwei, et al. Study on constitutive relations of compressed concrete subjected to action of freezing-thawing cycles[J]. Journal of Building Materials, 2013, 16(1): 17-23. (in Chinese)) |
| [10] |
覃丽坤, 宋玉普, 于长江, 等.双轴压混凝土在冻融循环后的力学性能及其破坏准则[J]. 2004, 21(2): 188-193. (QIN Likun, SONG Yupu, YU Changjiang, et al. Mechanical property and failure criterion for concrete under biaxial compressive stresses after cyclic freezing and thawing[J]. Engineering Mechanics, 2004, 21(2): 188-193. (in Chinese)) http://www.cqvip.com/QK/95324X/2004002/9892237.html
|
| [11] |
覃丽坤, 宋玉普, 陈浩然, 等. 双轴拉压混凝土在冻融循环后的力学性能及破坏准则[J]. 岩石力学与工程学报, 2005, 24(10): 1740-1745. ( QIN Likun, SONG Yupu, CHEN Haoran, et al. Mechanical property and failure criterion of concrete under biaxial tension and compression after freeze-thaw cycling[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(10): 1740-1745. DOI:10.3321/j.issn:1000-6915.2005.10.018 (in Chinese)) |
| [12] |
王立成. 不同种类混凝土冻融循环后双轴压压统一强度准则[J]. 水电能源科学, 2012, 30(1): 159-161, 215. ( WANG Licheng. Unified strength criterion for different types of concretes under biaxial compression subjected to freezing and thawing action[J]. Water Resources and Power, 2012, 30(1): 159-161, 215. (in Chinese)) |
| [13] |
段安. 受冻融混凝土本构关系研究和冻融过程数值模拟[D]. 北京: 清华大学, 2009. (DUAN An. Research on constitutive relationship of frozen-thawed concrete and mathematical modeling of freeze-thaw process[D]. Beijing: Tsinghua University, 2009. (in Chinese))
|
| [14] |
冀晓东, 宋玉普, 刘建. 混凝土冻融损伤本构模型研究[J]. 计算力学学报, 2011, 28(3): 461-467. ( JI Xiaodong, SONG Yupu, LIU Jian. Study on frost damage constitutive model of concrete[J]. Chinese Journal of Computational Mechanics, 2011, 28(3): 461-467. DOI:10.7511/jslx201103026 (in Chinese)) |
| [15] |
商怀帅, 曹磊, 王慧平, 等. 混凝土冻融损伤后双轴受力下的脆弹性损伤本构模型[J]. 江苏大学学报(自然科学版), 2014, 35(6): 727-731. ( SHANG Huaishuai, CAO Lei, WANG Huiping, et al. Brittle elastic damage constitutive model of plain concrete under biaxial compression after freeze-thaw cycles[J]. Journal of Jiangsu University(Natural Science Edition), 2014, 35(6): 727-731. (in Chinese)) |
| [16] |
苏捷, 方志, 杨钻. 混凝土单轴受压性能尺寸效应的试验研究[J]. 工业建筑, 2012, 42(6): 122-126. ( SU Jie, FANG Zhi, YANG Zuan. Experimental study on the size effect of concrete uniaxial compressive behavior[J]. Industrial Construction, 2012, 42(6): 122-126. (in Chinese)) |
| [17] |
肖福坤, 申志亮, 刘刚, 等. 循环加卸载中滞回环与弹塑性应变能关系研究[J]. 岩石力学与工程学报, 2014, 33(9): 1791-1797. ( XIAO Fukun, SHEN Zhiliang, LIU Gang, et al. Relationship between hysteresis loop and elastoplastic strain energy during cyclic loading and unloading[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(9): 1791-1797. (in Chinese)) |
| [18] |
殷有泉. 岩石的塑性、损伤及其本构表述[J]. 地质科学, 1995, 30(1): 63-69. ( YIN Youquan. On rock plasticity, damage and their constitutive formulation[J]. Scientia Geologica Sinica, 1995, 30(1): 63-69. (in Chinese)) |
2. College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China
 2017
2017 
