国内外许多座已建成的土石坝观测资料显示，坝体在竣工蓄水后仍然持续产生后期变形。除了库水位变化和降雨等干湿循环引起的堆石料湿化变形以外，坝体后期变形主要因素就是流变。长时间的流变会引起坝体应力分布不均匀, 恶化心墙及面板应力变形性状，导致心墙发生水力劈裂或面板裂缝, 直接危及大坝安全^[1]。堆石料的流变对于坝体的后期安全预测至关重要，研究堆石料的流变特性，提高对流变的认识水平有利于更好地评估坝体的安全性。

国内外很多学者开展了堆石料流变特性及机理的研究工作，对堆石颗粒的流变机理和规律，有一个比较共性的认识，即流变实质上是由于堆石颗粒在变形过程中不断破碎-重排的应力调整过程。随着时间的延长，颗粒破碎逐渐减少，堆石的流变变形也逐渐趋于稳定。这从颗粒破碎和重排的角度定性地解释了流变机理和规律。

近些年，分形理论成为研究颗粒破碎及粒状材料级配演变的重要工具，根据McDowell及Coop等^[2-3]的研究, 颗粒破碎后会趋于自相似分布, 呈现分形特征；分形与级配相关，很多学者也将分形理论应用于粗粒土缩尺方法研究；陈海洋等^[4-7]通过相关试验研究发现粒状材料的分形规律受加载条件和颗粒粒径影响，并且与颗粒破碎有一定的相关性；石修松等^[8]运用分形维数研究了堆石料的破碎特性, 发现破碎会导致分形维数的增大, 破碎后的分形维数与Marsal^[9]破碎指标有良好的线性关系。可见分形维数不仅可以描述粒径的大小、颗粒组成的均一程度，还可以用于描述单一粒径级配分布的集中程度, 能够较全面地反映颗粒破碎后的粒径分布状况，在研究颗粒破碎及级配演变方面具有较强的优势。

Xiao等^[10]在Einav等^[11]研究基础上，将分形维数引入堆石料级配表达式，从而将颗粒破碎率与分形维数建立联系，通过不同围压不同初始孔隙比的堆石料剪切试验分析了颗粒破碎对堆石料强度和变形的影响。在这个思路的启发下，考虑到棱角显著容易破碎的软岩堆石料，颗粒破碎引起的流变量较为可观，在前期较长时间内颗粒破碎是流变的主因，流变过程可以近似看作颗粒破碎或级配随时间演变的过程，这种情况下，粒状材料的分形理论同样可应用于堆石料流变过程分析。在此基础上，本文首先推导了两种可能的流变过程分形维数表达式，然后通过过程流变试验验证了双曲线型分形维数的合理性，最后结合贾宇峰等^[12]和Ueng等^[13]研究建立一个考虑颗粒破碎的流变本构模型。由于流变时间较长，试验用料有限，同时为了验证流变过程中堆石颗粒破碎率随时间的变化规律，需要同一级配下进行多组试验，以便确定不同时间停止的过程流变试验的颗粒破碎率，试验精度要求较高，筛分工作量大，周期较长，本文主要侧重单一围压单一偏应力试验结果的理论陈述，后续考虑不同试验条件以及分析本构模型的影响因素。

1 分形理论与颗粒破碎 1.1 分形理论与级配

自相似性和分形是许多自然事物和现象的客观特征。Mandelbrot^[14]建立了二维空间的颗粒大小分形特征模型；Tyler等^[15]对该模型进行了推广，建立了三维空间的粒径分布分维模型。贾荷花等^[16]进一步指出分形理论在颗粒物研究中的应用价值。本文主要在三维空间分形模型基础上，通过假设不同的粒级土体具有相同的密度等条件，用颗粒质量代替颗粒的体积，推导出计算土体粒径分布分形维数的质量分布模型，以此研究堆石料颗粒破碎的分形特性^[8]。

在三维空间中，大于某一特征尺度d_i的土颗粒构成的体积为：

$ V\left( {\rho > {d_i}} \right) = {C_{\rm{V}}}\left[{1-{{\left( {\frac{{{d_i}}}{{{\lambda _{\rm{V}}}}}} \right)}^{3-D}}} \right] $

(1)

式中：D为分形维数；C_V, λ_V均为常数，与颗粒的大小、形状相关。设M_T为总质量, M(ρ < d_i)为粒径小于d_i颗粒的质量，由上述关系可得：

$ \frac{{M\left( {\rho < {d_i}} \right)}}{{{M_{\rm{T}}}}} = {\left( {\frac{{{d_i}}}{{{d_{\max }}}}} \right)^{3-D}} $

(2)

式中：d_max为最大颗粒粒径。

根据土体级配的定义，相应的级配曲线为：

$ \varphi \left( d \right) = {\left( {\frac{d}{{{d_{\max }}}}} \right)^{3-D}} $

(3)

分形维数反映了颗粒破碎后粒径的大小及分布的均匀程度。分形维数越大，复杂形体占有空间的有效性越高，破碎量越大。流变过程中颗粒不断破碎，分形维数随时间不断增大并趋于稳定，假定D_t=f(t)。流变过程中级配随时间的变化可表示为：

$ \varphi \left( d \right) = {\left( {\frac{d}{{{d_{\max }}}}} \right)^{3-f\left( t \right)}} $

(4)

式中：f(t)为流变过程中分形维数随时间的函数关系式。

1.2 颗粒破碎率与时间的关系

对于初始级配，根据级配曲线选择数据点，用y=mxⁿ形式函数拟合，其中x对应颗粒粒径d，然后级配曲线进一步转化成为$\varphi \left( d \right) = {\left( {\frac{d}{{{d_{\max }}}}} \right)^{3-{D_0}}} $。若$\int_0^{{d_{\max }}} {{{\left( {\frac{d}{{{d_{\max }}}}} \right)}^{3-{D_0}}}{\rm{d}}\left( {\lg d} \right) = \int_0^{{d_{\max }}} {m{d^n}{\rm{d}}\left( {\lg d} \right)} } $，则堆石颗粒初始分形维数${D_0} = 3-\frac{n}{{md_{\max }^{n-1}}} $。

根据文献[8]的堆石料三轴试验颗粒破碎成果，在常规高围压下，颗粒破碎率达到30%时，分形维数约为2.7左右。若要进一步提高颗粒破碎率以提高试验后的分形维数，需要越来越高的围压，考虑到后文涉及的试验围压为2.6 MPa，并且试样初始分形维数较低，若达到30%的颗粒破碎率则需要的流变时间将会很长，甚至难以达到30%的颗粒破碎率，因此本文假定此种情况对应的最终分形维数D_u=2.7，以便于后续计算。值得注意的是，粒状材料其实很难达到最终分形维数D_u，并且最终分形维数D_u与颗粒材料属性有关，若材料易破碎，则材料达到的最终分形维数越大，更接近最大分形维数3。

堆石料流变过程是颗粒不断滑移、破碎和重排的过程，前期颗粒体系剧烈变化，后期颗粒体系逐渐平衡至稳定。在整个过程中，颗粒破碎率随时间的增长率逐渐减小直至为零，最终堆石颗粒不再破碎。根据流变过程中颗粒破碎率随时间的变化规律，假定流变过程中分形维数表达式为D_t=ω(t)，则D_t需满足如下条件：

$ {D_t} = \left\{ \begin{array}{l} {D_0}, t = 0\\ {D_{\rm{u}}}, t = + \infty \end{array} \right. $

(5)

式中：D₀为初始分形维数；D_u为最终分形维数。同时考虑D_t前期增长较快，后期增长较为缓慢，即dD_t/dt为时间t的减函数。

借鉴流变理论中体变和剪应变随时间的变化规律，可得流变过程中分形维数具有指数和双曲线两种形式，表达式分别为：D_t=D₀exp(－at)+D_u(1－exp(－at))和${D_t} = \frac{{\left( {{D_{\rm{u}}}-{D_0}} \right)t}}{{a + t}} + {D_0} $，其中a为参数。若级配曲线中粒径横坐标采用对数坐标，具体如图 1，可根据堆石颗粒流变过程中的初始级配φ₀，t时刻的级配φ_t，以及最终级配φ_u确定流变过程中颗粒破碎率随时间的变化，得到颗粒破碎率B_r:

$ {B_{\rm{r}}} = \frac{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _t}-{\varphi _0}} \right){\rm{d}}\left( {\lg d} \right)} }}{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _{\rm{u}}}-{\varphi _0}} \right){\rm{d}}\left( {\lg d} \right)} }} = \frac{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _t}-{\varphi _0}} \right){d^{ - 1}}{\rm{d}}d} }}{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _{\rm{u}}} - {\varphi _0}} \right){d^{ - 1}}{\rm{d}}d} }} = \frac{{\left( {{D_t} - {D_0}} \right)\left( {3 - {D_{\rm{u}}}} \right)}}{{\left( {{D_{\rm{u}}} - {D_0}} \right)\left( {3 - {D_t}} \right)}} = \xi \left( t \right) $

(6)

对于指数型分形维数D_t，颗粒破碎率为:

$ \zeta \left( t \right) =-\frac{{3-{D_{\rm{u}}}}}{{{D_{\rm{u}}}-{D_0}}} + \frac{{\left( {3 - {D_0}} \right)\left( {3 - {D_{\rm{u}}}} \right)}}{{\left( {{D_{\rm{u}}} - {D_0}} \right)\left( {3 - {D_t}} \right)}} = {r_1} + \frac{1}{{{r_2} + {r_3}\exp \left( { - at} \right)}} $

(7)

式中：$r =-\frac{{0.3}}{{2.7-{D_0}}}, {r_2} = \frac{{2.7-{D_0}}}{{3 - {D_0}}}, {r_3} = \frac{{{{\left( {2.7 - {D_0}} \right)}^2}}}{{0.3\left( {3 - {D_0}} \right)}} $。

对于双曲线型分形维数D_t, 颗粒破碎率为：

$ \zeta \left( t \right) =-\frac{{3-{D_{\rm{u}}}}}{{{D_{\rm{u}}}-{D_0}}} + \frac{{\left( {3 - {D_0}} \right)\left( {3 - {D_{\rm{u}}}} \right)}}{{\left( {{D_{\rm{u}}} - {D_0}} \right)\left( {3 - {D_t}} \right)}} = {s_1} + \frac{{a + t}}{{{s_2}a + {s_3}t}} $

(8)

式中：${s_1} = \frac{{0.3}}{{2.7-{D_0}}}, {s_2} = \frac{{2.7-{D_0}}}{{0.3}}, {s_3} = \frac{{2.7-{D_0}}}{{3 - {D_0}}} $。

2 堆石料的过程流变试验 2.1 试验安排及说明

为了研究堆石料流变过程中的颗粒破碎率随时间的变化，需要针对同一试样以流变时间为变量进行不同流变时间的过程流变试验，以验证哪一种流变过程颗粒破碎率表达式较为适合。对于三轴流变试验，每级荷载需要维持7~10 d或更长，而流变过程中的颗粒破碎和体积流变变形主要发生在流变初期，另外本文所用的堆石料在20 h以后体积流变变形很小，因此本研究主要进行24 h以内的过程流变试验，即相同级配的堆石料在相同围压下，先剪切再维持相同偏应力进行0，1，4，8和24 h三轴剪切流变试验，其中0 h的含义指只进行剪切试验。由于对湿堆石料晾晒筛分需要大量时间，本试验采用干样，试验结束后即可进行筛分。每次三轴堆石料流变试验均使用同一组试样，试样来源观音岩水电站，为砂岩堆石料，有一定的棱角，同时颗粒相对容易破碎，试样按孔隙率0.22控制制样密度，具体颗粒级配情况见表 1。

为了保证试验的精度，同时考虑到三轴流变试验中堆石颗粒主要为大粒径颗粒的棱角破碎，在常规筛子基础上自制30 mm和50 mm的筛子，以便在大粒径范围内更加细致地捕捉颗粒破碎情况。

由于本试验以流变时间为变量追踪每个流变试验前后的颗粒破碎率，因此需保证制样、固结和施加偏应力的一致性。初次试验时试样经过试振，确定后续每次试验试样分5层装入护筒，每层振动时间为50 s，以便制成的试样保持尽量相似的密实度。试验围压为2.6 MPa，最终偏应力为354 kN，对应5 MPa。每次试验围压均施加至2.6 MPa，维持相同固结时间，然后以相同加载速率逐渐施加偏应力至5 MPa，同样维持相同时间；然后维持恒定荷载，以偏应力刚加至5 MPa时为流变起始时间，进行不同流变时间的过程流变试验。本次试验，流变过程中颗粒破碎率约达7%，主要原因在于剪切过程中颗粒破碎并不完全，从而在流变阶段特别是流变初始阶段同样产生较大的颗粒破碎。

2.2 分形维数的确定

对室内大三轴流变级配曲线，采用如下方法拟合：自定义拟合函数$y = {\left( {\frac{x}{{{d_{\rm{M}}}}}} \right)^\alpha } $或者$y = 100{\left( {\frac{x}{{{d_{\rm{M}}}}}} \right)^\alpha } $，其中d_M对应最大粒径，x和y分别对应堆石料粒径和小于此粒径堆石料所占质量百分比，这样根据级配曲线即可确定出分形维数D=3－α，假定最终分形维数为D_u=2.7，初始试样分形维数为D₀，当前试验分形维数为D_t，于是颗粒破碎率$ {B_{\rm{r}}} = \frac{{\left( {{D_t}-{D_0}} \right)\left( {4-{D_{\rm{u}}}} \right)}}{{\left( {{D_{\rm{u}}}-{D_0}} \right)\left( {4 - {D_t}} \right)}}$。根据试验所设计的级配，采用上述方法可得此种堆石料初始级配对应的分形维数为D₀=2.461 3。

2.3 颗粒破碎率的计算

颗粒破碎率的计算采用Xiao等^[10]对塔城堆石料(TRM)的计算方法, 该方法在Einav^[11]基础上将分形维数引入堆石颗粒级配，通过分形维数变化计算颗粒破碎率。考虑本次试验组数较多，每次试验结束后均需进行筛分，对于颗粒粒径大于5 mm的堆石颗粒筛分工作相对省力，若继续筛分5 mm以下堆石颗粒，工作量变得巨大，本次试验只将堆石颗粒筛至5 mm，不再细致筛分。在处理级配曲线时，由于没有细颗粒级配数据，粒径横坐标不再采用Xiao等^[10]使用的对数坐标，而采用常规坐标，颗粒破碎率的推导需稍作变化，将式(6)中的d(lgd)改为dd，推导过程如下：

$ {B_{\rm{r}}} = \frac{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _{\rm{t}}}-{\varphi _0}} \right){\rm{d}}d} }}{{\int_{{d_m}}^{{d_{\rm{M}}}} {\left( {{\varphi _{\rm{u}}}-{\varphi _0}} \right){\rm{d}}d} }} = \frac{{\left( {{D_t}-{D_0}} \right)\left( {4 - {D_{\rm{u}}}} \right)}}{{\left( {{D_{\rm{u}}} - {D_0}} \right)\left( {4 - {D_t}} \right)}} $

(9)

式(9)仅用于确定本文过程流变试验不同时间的颗粒破碎率，以此为基础数据，进一步确定常用的对数坐标下的分形维数对应的颗粒破碎表达式(7)和式(8)中的各个参数。

2.4 流变过程中颗粒破碎率

经过大量的颗粒破碎试验，剔除误差较大试验数据，并结合式(9)计算颗粒破碎率，可得堆石颗粒不同流变时间结束后的级配和颗粒破碎率(见表 2)。0, 1，4，8，14 h过程流变试验对应的最终颗粒破碎率分别为11.642%，16.858%，17.084%，18.103%和18.897%。

根据1.2节的论述，假定流变过程中分形维数按照指数和双曲线两种形式变化，可得颗粒破碎率随时间变化的两种形式，即B_r(t)=r₁+1/(r₂+r₃exp(－at))和B_r(t)=s₁+(a+t)/(s₂a+s₃t)，用这两种形式拟合流变过程颗粒破碎率随时间变化。对于两种类型的颗粒破碎率，考虑t=0, B_r=0.116 42，即剪切阶段颗粒破碎率为11.642%，可得r₁+1/(r₂+r₃)=0.116 42或s₁+1/(s₂+s₃)=0.116 42。根据流变过程中颗粒破碎率与时间的关系，假定试样在本试验应力条件下，流变时间足够长，最终颗粒破碎率为0.192，即t→∞, B_r=0.192，则r₁+1/r₂=0.192或s₁+1/s₂=0.192。若定义b=r₂/r₃或s₂/s₃, 则B_r=f(t, b, a)，其中a为流变分形维数D_t中的参数。

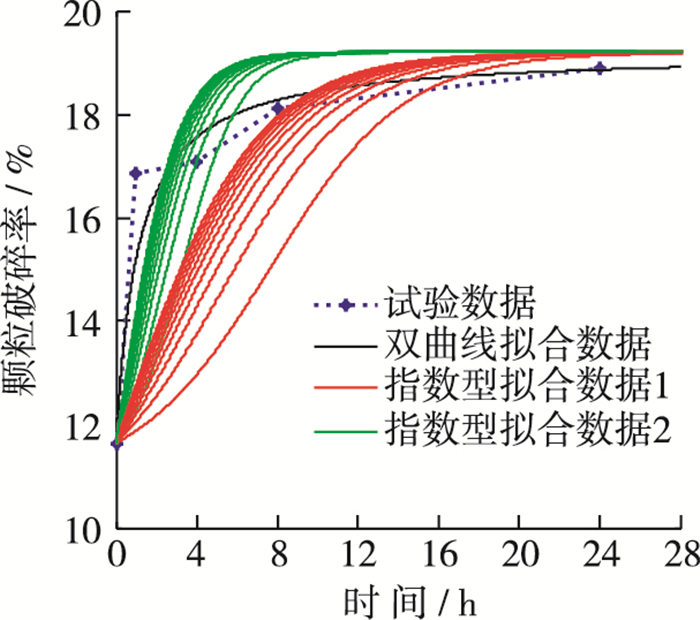
若采用双曲线型函数拟合, 对于a=1.02~2.02, b=1.01~3.01, 拟合曲线波动范围如图 2所示，a，b适当取值可保证拟合曲线在初始阶段与试验结果相差不大，并在24 h后收敛于最终颗粒破碎率。经对比，选取a=1.02, b=1.01对应的参数值，拟合参数s₁，s₂，s₃，a的较优拟合值分别为-0.639 6，1.322 8，1.202 5，1.02。较优值参数拟合曲线与试验曲线如图 3。图 4中绿线和红线为采用指数型函数拟合结果，绿线对应a=0.7, b=0.1~1.0的拟合结果，红线对应a=0.3, b=0.1~1.0拟合结果。这两种拟合结果相当于指数形式函数多种拟合曲线的两个边界，从图 4中可以看出绿线拟合结果收敛过快，24 h前已收敛至最终颗粒破碎率，与基本试验规律相差较大；红线拟合结果满足24 h收敛于定值的条件，但是初期颗粒破碎率与试验值比较过低，这说明指数型函数拟合难以兼顾最终收敛和初始值接近实际的条件。因此拟合堆石颗粒流变过程中颗粒破碎率与时间的变化采用双曲线型更加适合，也就是流变过程中分形维数随时间的变化采用双曲线型更适合，即D_t=(D_u－D₀)t/(a+t)+D₀，本文后续的体变规律验证采用双曲函数变化的分形维数D_t，同时以此为基础确定流变过程中的颗粒破碎率。

3 基于分形理论的流变本构模型及验证 3.1 理论推导

Ueng和Chen研究了砂土在排水剪切试验条件下考虑破碎的能量关系^[13]，贾宇峰等^[12]在此基础上进一步分析了考虑颗粒破碎的堆石料三轴剪切过程能量关系，对于常规三轴剪切试验：

$ \frac{{{\sigma _1}}}{{{\sigma _3}}} = \left( {1 + \frac{{{\rm{d}}\varepsilon _{\rm{V}}^p}}{{{\rm{d}}\varepsilon _1^p}}} \right){\tan ^2}\left( {{{45}^ \circ } + \frac{{{\varphi _{\rm{f}}}}}{2}} \right) + \frac{{{\rm{d}}{E_{\rm{B}}}}}{{{\sigma _3}{\rm{d}}\varepsilon _1^p}}\left( {1 + \sin {\varphi _{\rm{f}}}} \right) $

(10)

$ p = \frac{{{\sigma _1} + 2{\sigma _3}}}{3} $

(11)

$ q = {\sigma _1}-{\sigma _3} $

(12)

$ {\rm{d}}{\varepsilon _{\rm{s}}} = \frac{2}{3}\left( {{\rm{d}}{\varepsilon _1}-{\rm{d}}{\varepsilon _3}} \right) $

(13)

$ {\rm{d}}{\varepsilon _{\rm{V}}} = {\rm{d}}{\varepsilon _1} + 2{\rm{d}}{\varepsilon _3} $

(14)

滑动摩擦角φ_f与p-q平面内土体的临界状态线斜率M_cr的关系：

$ {\tan ^2}\left( {{{45}^ \circ } + \frac{{{\phi _{\rm{f}}}}}{2}} \right) = \frac{{1 + \sin {\phi _{\rm{f}}}}}{{1-\sin {\phi _{\rm{f}}}}} = \frac{{3 + 2{M_{{\rm{cr}}}}}}{{3-{M_{{\rm{cr}}}}}} $

(15)

综合以上，可得：

$ p{\rm{d}}\varepsilon _{\rm{V}}^p + q{\rm{d}}\varepsilon _{\rm{s}}^p = {M_{{\rm{cr}}}}p{\rm{d}}\varepsilon _{\rm{s}}^p + \frac{{2q-3p}}{9}{M_{{\rm{cr}}}}{\rm{d}}\varepsilon _{\rm{V}}^p + \frac{{\left( {3-{M_{{\rm{cr}}}}} \right)\left( {6 + 4{M_{{\rm{cr}}}}} \right)}}{{3\left( {6 + {M_{{\rm{cr}}}}} \right)}}{\rm{d}}{E_{\rm{B}}} $

(16)

剪切过程中满足土体能量平衡方程的滑动摩擦系数M是变化的，上式改为：

$ p{\rm{d}}\varepsilon _{\rm{V}}^p + q{\rm{d}}\varepsilon _{\rm{s}}^p = Mp{\rm{d}}\varepsilon _{\rm{s}}^p + \frac{{2q-3p}}{9}M{\rm{d}}\varepsilon _{\rm{V}}^p + \frac{{\left( {3-M} \right)\left( {6 + 4M} \right)}}{{3\left( {6 + M} \right)}}{\rm{d}}{E_{\rm{B}}} $

(17)

对于三轴流变过程，假定流变过程中土体中的颗粒与剪切过程类似都沿着同一个方向滑动，同时假定流变过程中滑动摩擦角ϕ_f与临界状态线斜率M关系与剪切过程相同，流变过程中σ₁, σ₃不变，时间t为变量。由颗粒滑动过程中的能量平衡仍可建立能量平衡关系式(17)，式(17)中dE_B=γdζ(t)，ζ(t)为流变过程中的颗粒破碎率。

一般而言，剪切和流变过程中滑动摩擦系数是变化的，滑动摩擦系数M与堆石颗粒破碎耗能E_B成反相关关系，若作此假设，则M为一个随时间变化的量，对式(17)积分求解体变将变得很麻烦，同时堆石颗粒流变过程中颗粒滑动及破碎远没有剪切过程剧烈，为了求解的方便，仍将M作为定值处理。流变过程荷载恒定，在此假定流变过程中弹性体应变和弹性剪应变增量：dε_V^e=0，dε_s^e=0，从而

$ {\rm{d}}{\varepsilon _{\rm{V}}} = {\rm{d}}\varepsilon _{\rm{V}}^p, {\rm{d}}{\varepsilon _{\rm{s}}} = {\rm{d}}\varepsilon _{\rm{s}}^p $

(18)

考虑三轴试验流变过程中：

$ {\varepsilon _{\rm{V}}} = {\varepsilon _1} + 2{\varepsilon _3}, {\varepsilon _{\rm{s}}} = \frac{2}{3}\left( {{\varepsilon _1}-{\varepsilon _3}} \right) $

(19)

若试验中监测到ε₁=g(t)，则${\varepsilon _{\rm{s}}} + \frac{1}{3}{\varepsilon _{\rm{V}}} = g\left( t \right) $。整个剪切和流变过程中：$g\left( t \right) = \frac{{\alpha t}}{{\beta + t}} + {\varepsilon '_1} $，ε′₁为剪切过程中产生的轴应变。将流变开始时的轴应变清零，则流变过程中轴应变表达式为：$g\left( t \right) = \frac{{\alpha t}}{{\beta + t}} $，α, β可由试验的轴向流变应变与时间关系曲线拟合得到。

同理流变过程中的颗粒破碎率若以堆石颗粒开始流变为起始点，则颗粒破碎率的以下计算式同样需要修正：$\zeta \left( t \right) = {s_1} + \frac{{a + t}}{{{s_2}a + {s_3}t}} $。修正时，需满足条件：t=0, ζ(t)=0，则$\zeta \left( t \right) = \frac{{a + t}}{{{s_2}a + {s_3}t}} $。

由流变阶段颗粒滑移破碎过程中的能量关系式(17)~(19)，可得三轴流变中的体变ε_V对时间的导数：

$ \frac{{{\rm{d}}{\varepsilon _{\rm{V}}}}}{{{\rm{d}}t}} = \frac{{\frac{{\left( {3-M} \right)\left( {6 + 4M} \right)}}{{3\left( {6 + M} \right)}}\frac{{{\rm{d}}{E_{\rm{B}}}}}{{{\rm{d}}t}} + \left( {Mp-q} \right)\frac{{{\rm{d}}g\left( t \right)}}{{{\rm{d}}t}}}}{{\left( {p-\frac{q}{3}} \right)\left( {1 + \frac{{2M}}{3}} \right)}} $

(20)

颗粒破碎率对时间求导：

$ \frac{{{\rm{d}}{E_{\rm{B}}}}}{{{\rm{d}}t}} = \frac{{\gamma a\left( {{s_2}-{s_3}} \right)}}{{{{\left( {a{s_2} + {s_3}t} \right)}^2}}} $

(21)

流变过程中的轴应变对时间求导：

$ \frac{{{\rm{d}}g\left( t \right)}}{{{\rm{d}}t}} = \frac{{\alpha \beta }}{{{{\left( {\beta + t} \right)}^2}}} $

(22)

流变开始时同样对体变进行清零，仅计算流变阶段体变考虑初始条件：t=0, ε_V(t)=0，可得:

$ {\varepsilon _{\rm{V}}} = \frac{{6\left( {6-2M} \right)\gamma }}{{\left( {6 + M} \right)\left( {3p-q} \right)}}\left( {\frac{{a + t}}{{{s_2}a + {s_3}t}}-\frac{1}{{{s_2}}}} \right) + \frac{{9\left( {Mp - q} \right)at}}{{\left( {3p - q} \right)\left( {3 + 2M} \right)\left( {\beta + t} \right)}} $

(23)

同时ε_s=ε₁－ε_V/3，由此可得流变过程中的ε_V和ε_s关于时间t的表达式。

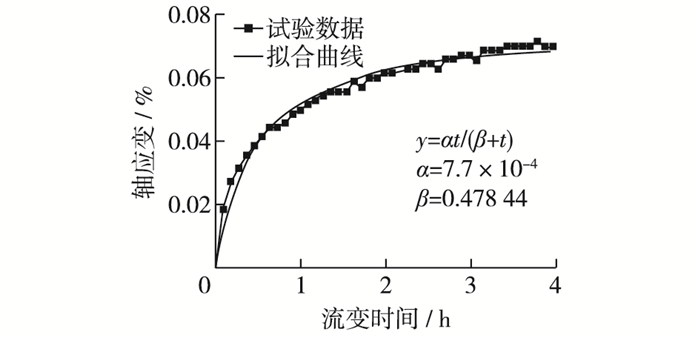
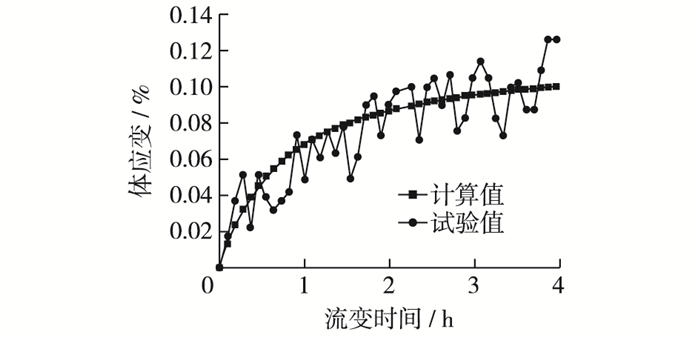
3.2 试验验证

为了验证体变计算式(23)的合理性，本文用4 h的过程流变试验数据进行验证，围压σ₃=2.6 MPa，偏应力σ₁－σ₃=5.0 MPa。试验中的颗粒级配同表 1，由于是干样，采用三轴流变仪围压控制系统的侧位移变化来近似计算体变，对试验中的轴应变变化采用函数拟合确定α，β值，如图 5所示。临界状态线斜率M取1.58，参数s₁, s₂, s₃, a的取值分别为-0.639 6，1.322 8，1.202 5，1.02。对于γ的取值，Salim等^[17]曾研究过粗颗粒在剪切过程中破碎耗能增量与颗粒破碎率增量的关系，剪切过程中二者呈线性关系。本文所用堆石料岩性不同，缺少相关试验研究，通过调整最终取为0.041，4 h过程流变试验的具体参数如表 3。过程流变试验所用的试样为干样，不能采用试样排水来测体变，只能采用三轴流变仪围压控制系统的侧位移变化来近似计算体变。由于三轴流变仪性能有限，体变值出现了跳跃的情况，采用推导得到的体变计算式与试验值进行对比，尽管试验体变值发生跳跃，但是总体趋势仍符合流变规律，计算结果与试验结果对比吻合较好，如图 6所示，这一点说明了堆石颗粒流变过程中颗粒破碎率按双曲函数变化的合理性。

3.3 模型特点

模型反映了堆石料流变过程中分形维数的变化，通过分形维数的变化可以推导堆石料破碎率的变化，由此可以统一堆石料剪切和流变过程中的颗粒破碎率变化，有利于建立统一的黏弹塑性本构模型。模型参数a可以反映围压或者应力水平以及岩性对堆石料流变快慢的综合影响，而初始级配对堆石料流变的影响可以体现在参数s₁, s₂, s₃上。模型可以基本反映流变过程的应变变化，但试样的内部和外部性质对参数的影响很难定量化，这里只是初步研究，流变试验制样精度和应变精度的控制也是制约参数定量化的重要影响因素。

4 结语

在分形理论框架下，将分形理论应用于堆石料流变，推导了两种可能的流变过程分形维数表达式，并给出了流变过程颗粒破碎率与分形维数的关系；进行了一系列同一级配试样不同时间的过程流变试验，通过分析过程流变试验中颗粒破碎率的变化，验证了流变过程中分形维数按双曲函数变化的合理性；最后在文献[13]研究的基础上，推导了流变过程中的堆石颗粒体应变变化规律，并通过试验验证了流变模型的合理性。本文从分形理论的角度，以分形维数和颗粒破碎为切入点，阐释了堆石料的流变规律，为建立统一的黏弹塑性本构模型建立基础。本文试验数量较少，仅在同一围压同一偏应力下进行多个过程流变试验，岩性、围压、应力水平、初始级配对模型参数的影响均需要进一步研究。