2. 河海大学 水文水资源与水利工程科学国家重点实验室,江苏 南京 210098;
3. 浙江海洋大学,浙江 舟山 316000
安全监测模型是安全监测定量分析的主要工具,对效应量与原因量之间的关系进行定量描述,从而揭示效应量的变化规律,并对建筑物结构性态变化发展进行预测,在水库大坝及其基础、边坡工程等领域得到了广泛应用,并取得了良好的社会经济效益[1-4]。然而在港口码头安全监测模型研究方面的报道还十分有限,这主要是因为港口码头安全监测仪器的布设远没有水库大坝中完备。近年来,随着安全监控意识的加强,已有一些港口码头开始监测研究工作[5-9],但是这些研究还不够深入。高桩码头是一种适用于软土地基的港口码头,基础沉降、气候变化、冲刷、超负荷运行等因素会使码头出现裂缝[10-12]。裂缝主要受哪些因素影响、变化规律如何、采用怎样的模型对其进行分析,这些问题的研究对港口码头的安全运行至关重要。码头裂缝开合度实测数据序列是码头裂缝变化的宏观反映,本文从裂缝开合度的实测数据序列着手,利用过程线分析、特征值统计等定性分析结果,结合荷载规范等现有资料[13-16],探讨高桩码头裂缝的主要影响因素,构造其因子表达式,对码头裂缝开合度监测模型进行研究。
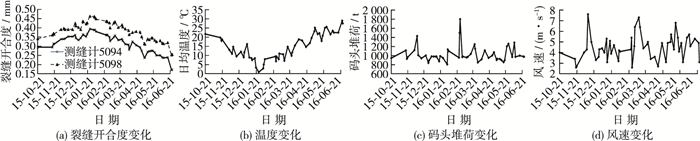
1 高桩码头裂缝开合度监测模型因子 1.1 定性分析定性分析方法主要有过程线图法和特征值统计法,过程线图法根据效应量和原因量分别随时间的变化过程线,分析效应量的影响因素及影响程度。图 1为某高桩码头裂缝开合度和环境量变化过程。
|
图 1 裂缝开合度和环境量变化 Figure 1 Process lines of crack opening displacement and other environment related parameters |
从图 1可知,高桩码头裂缝主要受温度、码头堆荷与风荷载的影响,尤其是温度及码头堆荷影响显著,一般在高温及堆荷量较低时期裂缝开合度减小,在低温及堆荷量较大时期裂缝开合度增加。除此之外,由于海水侵蚀、钢筋混凝土徐变及周期性波浪压力的作用,使得码头裂缝开合度产生时效变形。
1.2 高桩码头裂缝开合度理论统计模型高桩码头裂缝开合度主要由温度、风、堆荷和时效分量组成,即
| $ \delta = {\delta _{\rm{T}}} + {\delta _{\rm{W}}} + {\delta _P} + {\delta _\theta } $ | (1) |
式中:δ为裂缝开合度;δT为温度分量;δW为风压分量;δP为堆荷分量;δθ为时效分量。
(1) 温度分量(δT)。混凝土裂缝的形成和扩展对温度变化极其敏感,温度分量δT正是码头结构混凝土由于变温所引起的变形,该分量对码头裂缝总变形量影响较大。从力学观点来看,δT应选择码头混凝土中的温度计测值作为因子。当码头布设足够数量的温度计时,其测值便可以反映温度场;当码头内部没有布设温度计或只布设了极少量的温度计,而有气温资料时,采用气温测值。
根据弹性力学理论,在温度变化作用下,码头裂缝开合度与温度T有关,其表达式为:
| $ {\delta _{\rm{T}}} = \sum\limits_{i = 1}^k {{a_i}{T_i}} $ | (2) |
式中:Ti为各温度计的测值;ai为温度因子回归系数;k为温度计的支数,当只有气温资料时,取为1。
当气温随时间变化具有周期性时,温度分量可用周期函数项作为因子,其表达式为:
| $ {\delta _{\rm{T}}} = \sum\limits_{i = 1}^2 {\left( {{a_{1i}}\sin \left( {2{\rm{ \mathsf{ π} }}it/365} \right) + {a_{2i}}\cos \left( {2{\rm{ \mathsf{ π} }}it/365} \right)} \right)} $ | (3) |
式中:i=1~2,i=1为年周期,i=2为半年周期;t为从起始观测日开始计算的天数。
(2) 风压分量(δw)。由工程力学及相关理论可知,码头裂缝开合度与作用面上风速的2次方有关,即
| $ {\delta _{\rm{w}}} = b{v^2} $ | (4) |
式中:v为垂直于作用面上的风速值;b为风压因子回归系数。
(3) 堆荷分量(δP)。通过荷载分析,码头裂缝开合度的堆荷分量与码头堆荷量的1次方有关,即
| $ {\delta _P} = cP $ | (5) |
式中:P为码头堆荷量;c为堆荷分量的回归系数。
(4) 时效分量(δθ)。参考水工建筑物安全监控理论,选择多项式时效因子和对数时效因子,即
| $ {\delta _\theta } = {d_1}\theta + {d_2}\ln \theta $ | (6) |
式中:d1,d2为时效分量回归系数;θ为从起测日开始的天数乘以0.01。
2 高桩码头裂缝开合度监测模型建立建立统计模型是监测资料分析的一般方法。最小二乘支持向量机模型在处理非线性问题时表现出较强的稳健性和鲁棒性[17]。因此,本文主要建立裂缝开合度的统计模型和最小二乘支持向量机模型。
2.1 统计模型将各因子表达式代入式(1)可得:
| $ \delta = aT + b{v^2} + cP + {d_1}\theta + {d_2}\ln \theta $ | (7(a)) |
或
| $ \delta = \sum\limits_{i = 1}^2 {\left( {{a_{1i}}\sin \frac{{2{\rm{ \mathsf{ π} }}it}}{{365}} + {a_{2i}}\cos \frac{{2{\rm{ \mathsf{ π} }}it}}{{365}}} \right) + b{v^2} + cP + {d_1}\theta + {d_2}\ln \theta } $ | (7(b)) |
在实际建模时,为了避免初始因素的影响,选取相对值建立模型,即裂缝开合度统计模型表达式为
| $ \delta - {\delta _0} = a\left( {T - {T_0}} \right) + b\left( {{v^2} - v_0^2} \right) + c\left( {P - {P_0}} \right) + {d_1}\left( {\theta - {\theta _0}} \right) + {d_2}\left( {\ln \theta - \ln {\theta _0}} \right) $ | (8(a)) |
或
| $ \begin{array}{*{20}{c}} {\delta - {\delta _0} = \sum\limits_{i = 1}^2 {\left( {{a_{1i}}\left( {\sin \frac{{2{\rm{ \mathsf{ π} }}it}}{{365}} - \sin \frac{{2{\rm{ \mathsf{ π} }}i{t_0}}}{{365}}} \right) + {a_{2i}}\left( {\cos \frac{{2{\rm{ \mathsf{ π} }}it}}{{365}} - \sin \frac{{2{\rm{ \mathsf{ π} }}i{t_0}}}{{365}}} \right)} \right) + } }\\ {b\left( {{v^2} - v_0^2} \right) + c\left( {P - {P_0}} \right) + {d_1}\left( {\theta - {\theta _0}} \right) + {d_2}\left( {\ln \theta - \ln {\theta _0}} \right)} \end{array} $ | (8(b)) |
式中:δ0, T0, v0, P0, θ0分别为起始监测日对应的效应量及原因量监测值。a(或a1i, a2i),b, c, d1, d2为回归系数,通常采用多元回归或逐步回归等回归方法求得,其中逐步回归方程中只包含显著因子。
2.2 最小二乘支持向量机模型在裂缝开合度最小二乘支持向量机模型中,模型输入为引起裂缝变化的温度因子、堆荷因子、风压因子和时效因子x,模型输出为裂缝开合度y,样本集表示为Q={(x1, y1), (x2, y2), …, (xl, yl)},其中xl∈Rm为各个因子组成的m维列向量,yl为裂缝开合度测值,l为样本总数。
最小二乘支持向量机通过把数据集从输入空间映射到高维特征空间,将输入空间的非线性拟合问题转变为高维特征空间中的线性拟合问题,即
| $ y\left( \mathit{\boldsymbol{x}} \right) = {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( \mathit{\boldsymbol{x}} \right) + b $ | (9) |
式中:φ(x)为输入空间到高维特征空间的非线性映射函数;w为权向量;b为偏置量。
结合函数的复杂性和拟合误差,式(9)可归结为如下优化问题:
| $ \left\{ \begin{array}{l} \min J\left( {\mathit{\boldsymbol{w}}, b, \xi } \right) = \frac{1}{2}{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}} + \gamma \frac{1}{2}\sum\limits_{i = 1}^l {\xi _i^2} \\ {\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;{y_i} = {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\xi _i}, \;\;\;\;i = 1, 2, \cdots, l \end{array} \right. $ | (10) |
式中:超参数γ为正则化参数,用于避免过拟合;ξi为第i个样本点的训练误差。
建立Lagrangian方程
| $ L\left( {\mathit{\boldsymbol{w}}, b, \xi, a} \right) = J\left( {\mathit{\boldsymbol{w}}, b\;\xi } \right) - \sum\limits_{i = 1}^l {{a_i}\left\{ {{\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b - {y_i} + {\xi _i}} \right\}} $ | (11) |
式中:ai∈R为Lagrangian乘子,根据优化条件
| $ \partial L/\partial \mathit{\boldsymbol{w}} = 0, \partial L/\partial b = 0, \partial L/\partial {\xi _i} = 0, \partial L/\partial {a_i} = 0 $ | (12) |
可得:
| $ \mathit{\boldsymbol{w}} = \sum\limits_{i = 1}^l {{a_i}\varphi \left( {{x_i}} \right)}, \sum\limits_{i = 1}^l {{a_i}} = 0, {a_i} = \gamma {\xi _i}, {\mathit{\boldsymbol{w}}^{\rm{T}}}\varphi \left( {{x_i}} \right) + b + {\xi _i} - {y_i} = 0 $ | (13) |
消去变量w和ξ可得:
| $ \left[{\begin{array}{*{20}{c}} 0&{{1^{\rm{T}}}}\\ 1&{\mathit{\boldsymbol{ \boldsymbol{\varOmega} }} + {\mathit{\boldsymbol{\gamma }}^{-1}}\mathit{\boldsymbol{I}}} \end{array}} \right]\left[{\begin{array}{*{20}{c}} b\\ \mathit{\boldsymbol{a}} \end{array}} \right] = \left[{\begin{array}{*{20}{c}} 0\\ \mathit{\boldsymbol{y}} \end{array}} \right] $ | (14) |
式中:y=[y1, y2, L, yl]T, I=[1, 1, L, 1]T, a=[a1, a2, L, al]T,I为单位矩阵;Ω为核函数矩阵。在Ω矩阵中应用Mercer条件
| $ {\mathit{\Omega }_{ij}} = {y_i}{y_j}\varphi {\left( {{x_i}} \right)^{\rm{T}}}\varphi \left( {{x_i}} \right) = {y_i}{y_j}K\left( {{x_i}, {x_j}} \right) $ | (15) |
可得裂缝开合度最小二乘支持向量机模型为
| $ y\left( \mathit{\boldsymbol{x}} \right) = \sum\limits_{i = 1}^l {{a_i}K\left( {x, {x_i}} \right) + b} $ | (16) |
式中:ai, b为线性系统解;K(x, xi)为核函数。任意满足Mercer条件的对称函数均可作为核函数,常用核函数为多项式核函数、径向基核函数和Sigmoid函数,其中径向基核函数具有较好的统计性能,其表达式为:
| $ K\left( {x, {x_i}} \right) = \exp \left( { - \frac{{{{\left\| {x - {x_i}} \right\|}^2}}}{{2{\partial ^2}}}} \right), \partial > 0 $ | (17) |
将式(17)代入式(16)可得裂缝开合度最小二乘支持向量机回归函数为:
| $ y\left( x \right) = \sum\limits_{i = 1}^l {{a_i}\exp \left( { - \frac{{{{\left\| {x - {x_i}} \right\|}^2}}}{{2{\partial ^2}}}} \right) + b} $ | (18) |
裂缝开合度最小二乘支持向量机模型的主要参数是正则化参数γ和核参数
为进一步了解所建模型对裂缝开合度监测资料的处理效果,还需要对模型进行评价。对于拟合与回归模型的精度,常用的评价指标为复相关系数R与剩余标准差S,其计算方法如下:
| $ R = \sqrt {\sum\limits_{i = 1}^l {{{\left( {{{\delta '}_i} - \bar \delta } \right)}^2}} /\sum\limits_{i = 1}^l {{{\left( {{\delta _i} - \bar \delta } \right)}^2}} } \;\;\;\;\;\;\;\;S = \sqrt {\frac{1}{{{f_Q}}}\sum\limits_{i = 1}^l {{{\left( {{{\delta '}_i} - {\delta _i}} \right)}^2}} } $ | (19) |
式中:δ为效应量实测序列平均值;fQ为剩余平方和的自由度,fQ=l-m-1。
在评价模型效果时,除了模型精度之外,还需要考查模型的预测外延性,这对于建筑物的安全监控尤为重要。所谓预测外延性,是指模型在未来一段时间内的预测能力,通常采用绝对平均百分比误差MAPE、均方误差MSE和平均绝对误差MAE来衡量,其计算方法为:
| $ MAPE = \frac{1}{n}\sum\limits_{i = 1}^l {\left| {\frac{{{A_i} - {F_i}}}{{{A_i}}}} \right|}, MSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{A_i} - {F_i}} \right)}^2}/n} }, MAE = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {{A_i} - {F_i}} \right|} $ | (20) |
式中:n为测试样本的样本数;Ai为实测值;Fi为预测值。
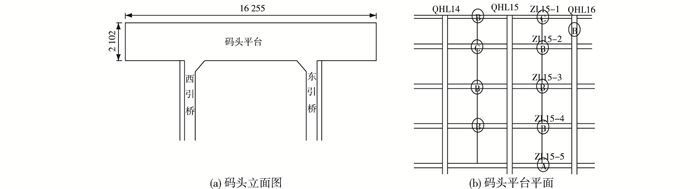
3 工程实例某高桩码头位于浙江省台州市椒江区,码头平台长162.55 m,宽14 m,主要构件为横梁、纵梁和面板,其结构简图如图 2所示。
|
图 2 码头结构简图(单位:cm) Figure 2 Diagram of wharf structure (unit: cm) |
在运行过程中,由于受到温度变化、风荷载、码头堆荷等作用,各构件存在混凝土胀裂、钢筋外露等侵蚀病害,图 2(b)中Ⓐ,Ⓑ,Ⓒ表示劣化等级逐渐增加。相关管理部门于2015年8月对其进行修复,修复过程中在纵梁ZL15-2,ZL15-3,ZL15-4,面板15-4等处布设了振弦式测缝计,从2015年10月21日开始对构件裂缝开合度变化情况进行监测,监测频次约每周1次。本文以位于纵梁ZL15-2南侧的测点5094和位于纵梁ZL15-3南侧的测点5098为例,采用2015年10月21日—5月26日的监测数据序列,其实测值和环境量变化过程线如图 1所示。由于数据序列相对较短,图 1(b)中气温变化的周期性不明显,利用式8(a)建立统计模型,其参数见表 1,同时建立最小二乘支持向量机模型,其参数见表 2。
| 表 1 统计模型系数 Table 1 Coefficients of statistical model |
| 表 2 最小二乘支持向量机模型参数 Table 2 Parameters of LSSVM model |
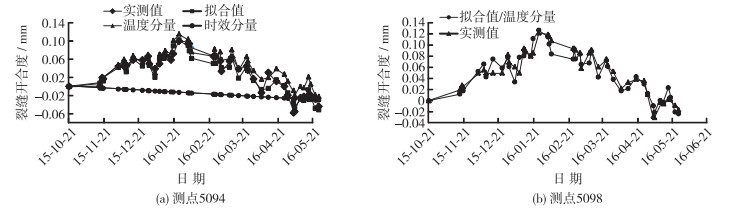
由表 1和2可以看出,统计模型和最小二乘支持向量机模型的复相关系数均在0.9以上,剩余标准差较小,相比于统计模型,最小二乘支持向量机模型的精度更高。为了进一步了解裂缝开合度和各分量之间的关系,找出裂缝开合度主要影响因素,采用上述逐步回归模型对各分量进行分离,实测值、拟合值和分量过程线如图 3所示。
|
图 3 典型测点实测值、拟合值与各分量变化过程线 Figure 3 Change curves of measured and fitted values and components of typical points |
由图 3可见,对于测点5094和测点5098,其实测值和拟合值均较为接近。温度分量是两个测点裂缝开合度变化的主要因素,验证了裂缝形成与扩展对温度变化极为敏感的结论,此外,测点5094裂缝开合度存在逐渐收缩的时效分量。风荷载对两个测点裂缝开合度变化的影响均不明显(风荷载因子没有被选入到逐步回归方程中),这主要与两测点在码头平台上所处的位置有关,至于码头堆荷(在该实例中其因子没有进入逐步回归方程)对两测点裂缝开合度影响不显著的原因及其影响规律还有待进一步收集数据利用长序列进行研究。
为验证模型的预测外延性,采用逐步回归模型和LSSVM模型对2016年6月份的测值进行预测,并对式(20)中各衡量参数进行计算,结果如表 3所示。
| 表 3 两种模型预测结果 Table 3 Prediction results of statistical model and LSSVM model |
由表 3可见,统计模型和最小二乘支持向量机模型均表现出一定的预测能力,从预测效果来看,最小二乘支持向量机模型优于统计模型,这主要是因为最小二乘支持向量机模型具有更强的稳健性和鲁棒性。需要指出的是,由于资料所限,本文仅对未来1个月的监测数据进行了预报。
4 结语本文针对高桩码头自身工作特点对其裂缝开合度监测模型进行了研究,指出高桩码头裂缝开合度的主要影响因素为温度、风、堆荷与时效,给出了各个影响因子的表达式,建立了高桩码头裂缝开合度的统计模型以及最小二乘支持向量机模型,探讨了模型效果的评价方法。将所建立的模型应用于浙江某高桩码头的裂缝监测,结果表明,两种模型的精度均较高,且具有一定的预测能力,这说明模型因子选取较为合理;另外,最小二乘支持向量模型的预测外延性优于统计模型,可用于高桩码头裂缝开合度的预警,而在分离各分量时建议采用逐步回归统计模型。本文为高桩码头裂缝开合度监测研究提供了一定依据,然而,高桩码头裂缝是一个受到众多因素影响的复杂非线性问题,在因子选择完备性与模型建立高效性方面还有待于进一步研究。
| [1] |
SALAZAR F, TOLEDO M Á, OÑATE E, et al. Interpretation of dam deformation and leakage with boosted regression trees[J]. Engineering Structures, 2016, 119: 230-251. DOI:10.1016/j.engstruct.2016.04.012 |
| [2] |
ISIDORI D, CONCETTONI E, CRISTALLI C, et al. Proof of concept of the structural health monitoring of framed structures by a novel combined experimental and theoretical approach[J]. Structural Control & Health Monitoring, 2016, 23(5): 802-824. |
| [3] |
SIGTRYGGSDOTTIR F G, SNÆBJÖRNSSON J T, GRANDE L, et al. Interrelations in multi-source geohazard monitoring for safety management of infrastructure systems[J]. Structure and Infrastructure Engineering, 2016, 12(3): 327-355. DOI:10.1080/15732479.2015.1015147 |
| [4] |
徐镇凯, 温勇兵, 魏博文, 等. 基于组合赋权模糊云理论的高边坡稳定性评价[J]. 水利水运工程学报, 2017(1): 10-17. ( XU Zhenkai, WEN Yongbing, WEI Bowen, et al. Stability evaluation method for high slope based on fuzzy cloud theory combined with weights[J]. Hydro-Science and Engineering, 2017(1): 10-17. (in Chinese)) |
| [5] |
葛浩, 黄耀坤, 朱鹏宇. 高桩码头在船舶撞击力作用下的应变监测研究[J]. 水运工程, 2015(1): 63-69. ( GE Hao, HUANG Yaokun, ZHU Pengyu. Strain monitoring of pile-supported wharf under action of ship collision[J]. Port & Waterway Engineering, 2015(1): 63-69. (in Chinese)) |
| [6] |
范庆来, 刘远财. 库水位涨落与降雨联合作用下绿草码头滑坡渗流场分布规律及稳定性分析[J]. 水电能源科学, 2015, 33(1): 115-118. ( FAN Qinglai, LIU Yuancai. Seepage field distribution and stability analysis of Lvcao wharf landslide under effects of water level fluctuation and rainfall[J]. Water Resources and Power, 2015, 33(1): 115-118. (in Chinese)) |
| [7] |
张崇. 基于组态软件的开敞式码头系泊监控系统研究[D]. 大连: 大连交通大学, 2015. (ZHANG Chong. Study on the open sea terminal mooring system based on configuration software[D]. Dalian: Dalian Jiaotong University, 2015. (in Chinese)) http://www.cqvip.com/QK/98194B/201504/664653447.html
|
| [8] |
李亚婷. 斜坡码头施工监测与预警控制研究[D]. 重庆: 重庆交通大学, 2014. (LI Yating. Reasearch on construction monitoring and early warning and control of slope wharf[D]. Chongqing: Chongqing Jiaotong University, 2014. (in Chinese)) http://d.wanfangdata.com.cn/Thesis/Y2559764
|
| [9] |
KHAYAT K H, TAGNIT-HAMOU A, PETROV N. Performance of concrete wharves constructed between 1901 and 1928 at the Port of Montreal[J]. Cement and Concrete Research, 2005, 35(2): 226-232. DOI:10.1016/j.cemconres.2004.05.047 |
| [10] |
KWON S J, NA U J, SANG S P, et al. Service life prediction of concrete wharves with early-aged crack: Probabilistic approach for chloride diffusion[J]. Structural Safety, 2009, 31(1): 75-83. DOI:10.1016/j.strusafe.2008.03.004 |
| [11] |
STEWART M G, WANG X M, NGUYEN, M N. Climate change impact and risks of concrete infrastructure deterioration[J]. Engineering Structures, 2011, 33(4): 1326-1337. DOI:10.1016/j.engstruct.2011.01.010 |
| [12] |
陈凤山. 海洋环境下钢筋混凝土结构CFRP加固研究[D]. 大连: 大连理工大学, 2007. (CHEN Fengshan. Research on coastal concrete structures strengthened with CFRP [D]. Dalian: Dalian University of Technology, 2007. (in Chinese)) http://d.wanfangdata.com.cn/Thesis/Y1205378
|
| [13] |
吴锋. 港口工程高桩码头结构性能退化研究[D]. 上海: 上海交通大学, 2015. (WU Feng. Study on performance degradation of high-piled wharf structure in port[D]. Shanghai: Shanghai Jiaotong University, 2015. (in Chinese))
|
| [14] |
韩理安, 席与耀. 港口水工建筑物[M]. 北京: 人民交通出版社, 2015. ( HAN Li'an, XI Yuyao. Port hydraulic structures[M]. Beijing: China Communications Press, 2015. (in Chinese))
|
| [15] |
王炳煌. 高桩码头工程[M]. 北京: 人民交通出版社, 2010. ( WANG Binghuang. Hige-piled wharf engineering[M]. Beijing: China Communications Press, 2010. (in Chinese))
|
| [16] |
陈达, 沈才华. 高桩码头结构分段设计理论和方法[M]. 北京: 科学出版社, 2012. ( CHEN Da, SHEN Caihua. Subsection design theory & its applications of high-piled wharf structures[M]. Beijing: Science Press, 2012. (in Chinese))
|
| [17] |
肖浩波, 谷艳昌. 混凝土坝安全监控最小二乘支持向量机模型[J]. 长江科学院院报, 2013, 30(5): 34-37. ( XIAO Haobo, GU Yanchang. Monitoring model for concrete dam safety using least square support vector machine[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(5): 34-37. (in Chinese)) |
| [18] |
CHEN Xudong, GU Chongshi, CHEN Haonan. Early warning of dam seepage with cooperation between principal component analysis and least squares wavelet support vector machine[J]. Fresenius Environmental Bulletin, 2013, 22(2): 500-507. |
2. State Key Laboratory of Hydrology-Water Resources and Hydraulic Engineering, Nanjing 210098, China;
3. Zhejiang Ocean University, Zhoushan 316000, China
 2017
2017 

