2. 华北水利水电大学 水利学院,河南 郑州 450045
渗流是引起水利工程水量损失、失稳破坏等诸多不良后果的重要原因。研究输水渠道的渗流场分布和降排水方案,对保证渠道工程安全及渗流稳定具有重要意义。地下水位较高、边坡土体渗透系数较小的大型渠道工程,其施工期的深井降水对工程规划、设计和实践有很大影响,因此,为了满足渠道工程安全稳定的需求,有必要研究渠道施工期的渗流场和降水措施。
在施工期,渠道降水井的布置对渗流场水头分布有较大影响,但诸如降水井影响半径等参数的选取十分困难。传统工程中对施工期渠道降水设计所依据的公式一般具有较多理想化的假设条件[1-6],虽然应用简单,但限制极多。近年来,随着计算机技术和有自由面无压渗流问题相关数值解法的发展,研究者逐渐将解决渠道渗流问题的重点转为数值模拟计算,并取得了一些成果。李斌等[7]采用改进的截止负压法对具体渠道工程不同时期的渗流场进行了三维数值模拟,评价了渠道边坡在不同阶段的渗控方案;崔皓东等[8]采用运算效率更高的节点虚流量法来模拟渠道渗流,并对不同种类渗控措施的效果进行了评价,取得了一系列研究成果。王金龙等[9]利用GMS中的Modflow对渠道建立三维渗流模型,计算给出了显著影响渠道降水效果的几点要素。上述研究证明了数值模拟在工程应用中的有效性,可以为实际工程提供必要的参考,但在不同降水井布置对具体渗控效果的影响及二者相关关系上缺乏详尽细致的分析,且限于计算方法原因,在稳定渗流条件下的计算效率较低,在自由面附近区域的计算精度不高。文献[10]提出了不变网格确定渗流自由面的节点虚流量法,克服了变网格法的缺陷;文献[11]又在此基础上提出了改进的节点虚流量全域迭代法,并通过具体工程实际和算例验证了使用该方法进行稳定渗流计算的可靠性和优越性。文献[10]提出的改进节点虚流量法严格扣除过渡区中的虚流量贡献,能更精细地刻画自由面和渗流溢出点的渗流场,对渠道、堤防等渗流场的模拟结果较其他方法更为精确。
基于此,本文利用改进节点虚流量法[10]求解渗流场,运用等效节点流量法[11]精确求解渗流量,在工程基础上对渠道渗流进行三维有限元分析[12-13],研究不同渗控措施和边界条件对渠道渗控效果的影响,为相似条件下的渠道施工提供参考。
1 改进节点虚流量法求解渗流场针对有自由面无压渗流场的数值模拟,根据文献[4],无压稳定渗流计算边界条件如图 1所示,渗流自由面将整个计算域分为了两部分,分别为Ω1(渗流实域)和Ω2(渗流虚域)。
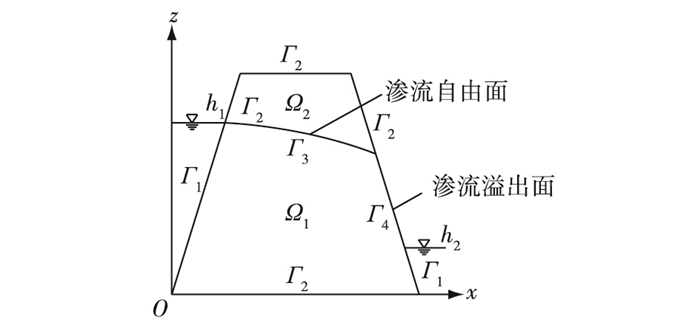
|
图 1 无压稳定渗流计算边界 Figure 1 Calculating boundary of unconfined seepage field |
根据达西定律[14],稳定饱和渗流场的支配方程为:
| $ \frac{{ - \partial }}{{\partial {x_i}}}\left( {{k_{ij}}\frac{{\partial h}}{{\partial {x_j}}}} \right) + Q = 0 $ | (1) |
式中:xi为三向坐标;kij为描述岩体的渗透各向异性的饱和渗透系数张量;h为水头,Q为源汇项。其边界条件如下:
| $ h\left| {{\mathit{\Gamma }_1}} \right. = {h_1} $ | (2) |
| $ {k_{ij}}\frac{{\partial h}}{{\partial {x_j}}}{n_i}\left| {{\mathit{\Gamma }_2}} \right. = {q_{\rm{n}}} $ | (3) |
| $ {k_{ij}}\frac{{\partial h}}{{\partial {x_j}}}{n_i}\left| {{\mathit{\Gamma }_3}} \right. = 0, h = {x_3} $ | (4) |
| $ {k_{ij}}\frac{{\partial h}}{{\partial {x_j}}}{n_i}\left| {{\mathit{\Gamma }_4} \geqslant 0} \right., h = {x_3} $ | (5) |
式中:h1为已知水头;ni为渗流边界面外法线方向余弦,i=1, 2, 3;Γ1为已知水头边界;Γ2为已知渗流量的渗流边界;Γ3为渗流溢出面;Γ4为渗流自由面;qn为法向流量函数(边界面),以流出为正[10]。
由于实际工程渗流自由面位置、逸出面大小及实际渗流域大小均为未知,是一个边界非线性的数值问题,所以需运用Galerkin加权余量法通过式(6)的迭代计算才能求得渗流场的真解。
| $ \mathit{\boldsymbol{Kh}} = \mathit{\boldsymbol{Q}} - {\mathit{\boldsymbol{Q}}_2} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} Q}}, {\rm{ }}\mathit{\boldsymbol{ \boldsymbol{\varDelta} Q}} = {\mathit{\boldsymbol{K}}_2}\mathit{\boldsymbol{h}} $ | (6) |
式中:K,h和Q分别为计算域Ω的总传导矩阵、节点水头列阵和节点等效流量列阵; ΔQ为渗流虚域所贡献的结点虚流量列阵。
计算域虚域的传导矩阵K2中,一部分由纯虚单元贡献,另一部分由过渡单元中的虚区贡献,难以求解。为提高K2的计算精度,式(7)引入加密高斯点技术和连续的罚函数求解过渡单元虚区贡献的传导矩阵Ke,有:
| $ {\mathit{\boldsymbol{K}}^{\rm{e}}} = \sum\limits_i^{{n_{\rm{g}}}} {\sum\limits_j^{{n_{\rm{g}}}} {\sum\limits_m^{{n_{\rm{g}}}} {{{\rm{W}}_i}{{\rm{W}}_j}{{\rm{W}}_m}(1 - {H_\varepsilon }\left( p \right))F({\xi _i}, {\eta _j}, {\zeta _m}){\rm{ }}\,\,\,\,\left( {i, j, m = 1, 2, 3} \right)} } } $ | (7) |
式中:i, j, m为三向坐标;ng为高斯点的加密个数;Wi, Wj, Wm是每个方向坐标的权重;F(ξi, ηj, ζm)为被积函数,括号内为高斯点坐标;Hε(p)为连续的罚函数[10]。
2 工程应用 2.1 工程概况某渠道工程长11.989 km,渠道的底宽为25 m,渠底高程取平均值28.1 m,堤顶高程34.43 m,渠道采用降水井降水。该渠道工程地下水含量丰富,为保证渠道施工期干地施工的要求和施工质量,避免渗透破坏,需对渠道工程的渗流场进行计算分析。渠道典型断面的土层从上到下依次为黏土、壤土、黏土、壤土和粉细砂。
渗透系数与许多因素有关,根据前期勘测资料,各土层的渗透系数为:壤土2.0×10-3 cm/s(1.73 m/d), 黏土5.9×10-4 cm/s(0.51 m/d), 粉细砂5.0×10-3 cm/s (4.32 m/d)。假定渠道左右岸潜水位相同,模拟施工期情况不考虑开挖过程中的渗流,为基坑已经开挖至建基面后基础工程施工期间的稳定渗流过程,且渠道未设置排水措施、未进行衬砌;土壤中的水是不可压缩的,忽略蒸发等作用的影响,并认为土壤为均质土壤,且土壤在渗流过程中保持不变。基于以上假定,将模拟区概化为均匀水平各项同性,竖直各向异性的三维稳定渗流系统。
2.2 有限元模型和工况选择为了精细模拟中网格划分和渗流计算的方便,将圆形降水井等面积简化为600 mm×600 mm的正方形,计算模型沿渠道纵向取一组降水井抽降水影响范围的一半。计算域的渠道上游截取边界、下游截取边界和渠底边界均视为隔水边界面;渠道或建筑物左右岸为已知水头边界;边坡及渠底考虑为可溢出边界;降水井边界设定为已知水头边界或可溢出边界,以控制其抽水量。将渠道两侧土体进行适当延长并对降水井附近的网格进行适当加密,以提高渗流计算的精度。渠段采用空间六面体八节点等参单元计算,基本方案模型节点数为48 474个,单元数为43 292个。图 2为基本方案P1的计算网格及降水井细部网格,其他方案的网格与之稍有差别。
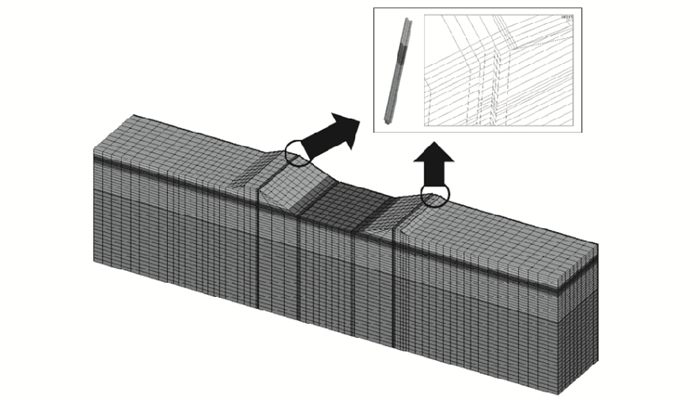
|
图 2 三维有限元计算网格及降水井细部网格 Figure 2 3D FEM calculating meshes and detailed meshes of dewatering well |
表 1为渗流计算方案。以渠道最低开挖面的中点为原点,建立笛卡尔坐标系。X轴表示渠道横向(左右岸方向),Y轴沿渠道纵向,Z轴为高度,下文涉及的水位均为此坐标系下的数值。表中基本方案P1中的渠道采用双排井点降水,非汛期情况下地下水位1.75 m,左右临空面地下水位相等,井点距坑壁1.5 m,埋置深度20 m。降水井采用无砂混凝土管,管井顺渠道纵向间距取60 m,渠道的典型横剖面如图 3(a)所示。方案P3与P5采用单排井点降水,在渠道纵轴线处布置,埋置深度12 m,典型横剖面如图 3(b)。其他计算方案的降水井布置如表 1所示。
| 表 1 计算方案 Table 1 Calculation cases |

|
图 3 渠道典型横剖面(单位:m) Figure 3 Typical sections of canal (unit: m) |
通过对渗流场模拟,得到了各方案施工期下渠道各剖面不同抽水水位下的水头等值线分布、水力坡降、降水井单井抽水量和渠底地下水位。
3.1 降水井剖面水头等值线分布将降水井抽水水位固定为-4 m进行渗流场计算,得到了各方案下降水井所在横剖面的水头等值线图。从P1基本方案水头等值线剖面图(图 4(a))可知,剖面水头等值线分布疏密有致,反映了渗控措施及边界条件对渗流场的影响,自由面由左右临空面潜水位1.75 m逐渐降低至降水井边界处的-4 m,且在降水井附近下降明显,水头等值线较为密集,在降水井间出现了明显的绕渗现象,整个渗流场的水头分布规律合理,表明降水井发挥了一定作用。但在渠底处,自由面隆起且水头高度仅为-0.24 m,不满足干地施工地下水位应降低至最低开挖面0.5 m以下的要求。
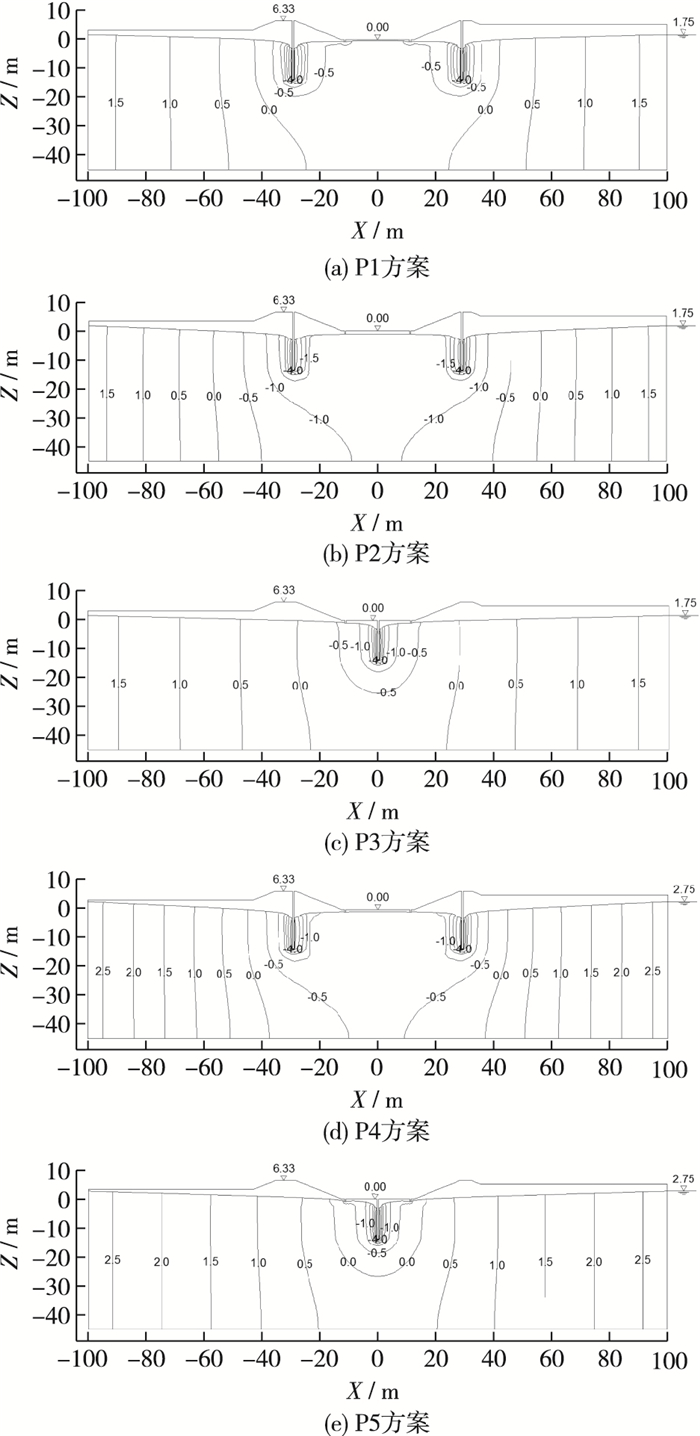
|
图 4 降水井剖面水头等值线分布(单位:m) Figure 4 Contours of hydraulic heads (unit: m) |
图 4(b)为方案P2的水头等值线剖面图。由图可知,渠底自由面较方案P1明显降低,降水井附近水头等值线分布也比P1稀疏,表明纵向降水井间距缩短后,密集布置的降水井排水降压的效果更为明显,渠底最高自由面水头高度为-1.148 m,满足干地施工的要求,起到了良好的降水效果。
方案P3在保持P2纵向间距的基础上将降排水措施改为单井布置,于渠底中心降水。由图 4(c)可知,该方案虽然减小了井的数量和埋置深度,使得水头等值线在降水井附近分布较为稠密,但大大降低了工程量,且渠底最高自由面水位为-0.579 m,满足渠道干地施工的要求,较前两个方案更加经济合理。
由图 4(d)和(e)可知,方案P4, P5在P2, P3的基础上抬高了左右临空面潜水位至2.75 m,水头等值线分布明显较潜水位1.75 m时稠密,渠底自由面水位升高,横向两个降水井之间的雍水更为明显。这表明地下潜水位高程对渠道降排水的效果影响明显,所以在工程前期准备时应加强对地下水位的勘测,在降排水设计中也应充分考虑各渗控措施在不同时期潜水位下的效果。
3.2 降水井边界水力坡降分析由水头等值线分布可得,水头等值线图的负梯度方向即为渗流方向,在降水井附近的水头等值线最为稠密,易发生渗透破坏。在降水井以下,壤土层与粉细砂层的交界面处水力坡降也值得关注。将降水井抽水水位固定为-4 m,可计算降水井边界和粉细砂层与壤土层交界面的最大水力坡降,图 5为各方案最大水力坡降计算结果对比,其中双排井布置情况选取产生最大水力坡降的左侧降水井边界进行水力坡降分析。
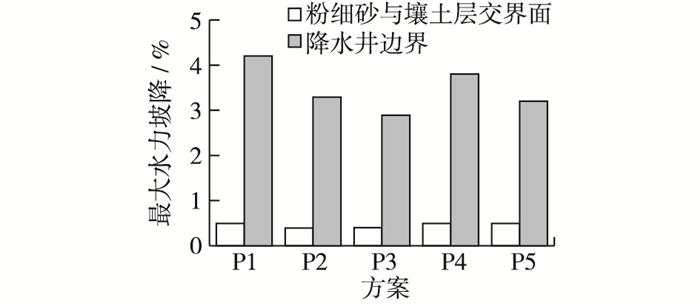
|
图 5 各方案最大水力坡降计算结果对比 Figure 5 Comparison of maximum hydraulic slope calculation results of cases |
由计算结果可知,对于降水井边界而言,基本方案P1的水力坡降值最大,相较于其他方案最易发生渗透破坏;P2的水力坡降较P1相对较小,说明降水井布置越密集,单井发生渗透破坏的可能性就越小。对比方案P2与P4, P3与P5可以发现,同样的渗控措施下,降水井边界的水力坡降对潜水位的变化极为敏感,左右临空面的潜水位越高,降水井边界就越容易发生渗透破坏。由图中不难看出,单井布置的P3方案发生渗透破坏的可能性最小,该方案下最为稳定。
由图 5可得,方案P1~P5在粉细砂层与壤土层交界面的水力坡降与降水井边界处水力坡降相比均较小,这表明渗流过程中土体内部的坡降较小,不易发生渗透破坏。
渠道渗流稳定不但与水力坡降有关,还与土体的粒径、级配及地层的相互关系等诸多因素有关。在施工期,长时间的降水可能引发地层沉降[15-16],因此,对于有渗透破坏风险的区域,还要进一步细观分析渗透破坏的发展和演化机理,为工程安全实施提供可靠保证。
3.3 降水要素对降水效果的影响改变降水井的抽水水位,计算各方案下单井抽水量和渠底地下水位的变化,结果如图 6~7所示。
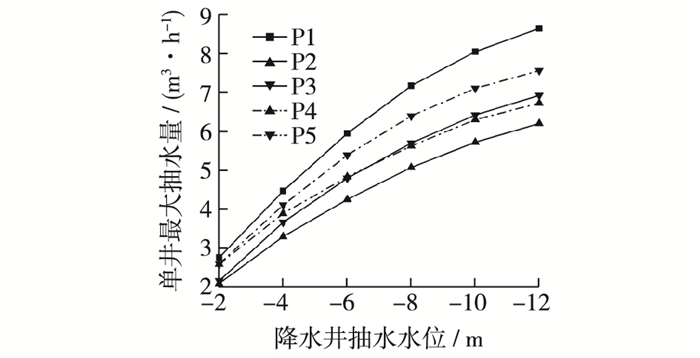
|
图 6 降水井抽水水位-单井最大抽水量关系 Figure 6 Relationship between water level and maximum seepage flow in a dewatering well |
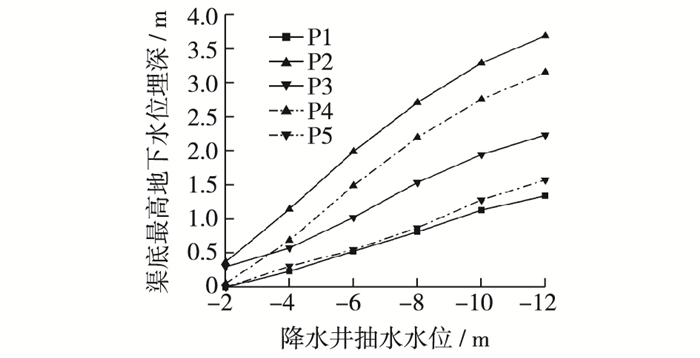
|
图 7 降水井抽水水位-渠底最高地下水位埋深关系 Figure 7 Relationship between water level in a dewatering well and maximum buried depth of groundwater level in canal bottom |
抽水量对渠底地下水位的影响较大,也反映了降水井的降排水能力。由图 6可知,随着降水井抽水水位的加深,单井抽水量逐渐增大,但趋势逐渐放缓,降水井抽水能力逐渐饱和。
由于方案P1的纵向布置间距大,影响区域广,故其单井抽水量最大。方案P2较方案P1整体抽水量下降明显,这表明降水井纵向间距的改变对降水井的抽水量影响显著。方案P3的抽水量较P2明显增大,其值介于P1与P2之间,这是由于该方案的单井承担了整个渠底的降水所造成。
对比P2与P4,P3与P5方案可知,相同的渗控方案下,潜水位的升高会导致抽水量的增加,对渗控效果的影响较大,在工程中应给予重视。
3.3.2 降水要素对渠底地下水位的影响图 7为降水井抽水水位与渠底最高地下水位埋深的关系,图中纵轴0.5 m处的横向辅助线代表干地施工的标准界限。由图可知,随着降水井抽水水位的加深,渠底地下水位不断降低,渠底最高地下水位的埋深不断增加。方案P1和P5的渠底地下水位与最低开挖面的距离最近,在-2和-4 m时的渠底最高地下水位埋深均小于0.5 m,不满足干地施工的要求;在抽水水位达到-6 m或更深时,所有方案的渠底最高地下水位埋深均大于0.5 m,满足干地施工的要求。因此认为,本工程将降水井的抽水水位选择在-6 m处较为经济合理。
对比P2与P4,P3与P5方案可知,相同的渗控方案下,潜水位升高,渠底最高地下水位也随之增大。渠底地下水位的增加是因抽水量的减小而导致的,过高的渠底地下水位对渠道干地施工不利,所以应严格控制降水井的抽水深度。
当降水井的抽水水位浅时,单井抽水量虽小,但渠底最高自由面过高,不能满足干地施工的要求;而抽水水位过深,不仅会使经济性欠佳,而且还会影响到渠底周边的地质环境[9],造成地面沉降和地下水资源的浪费。因此,应合理选择降水井的抽水水位,并尽量均匀对称地布置井管,使工程的渗控措施既经济又合理。
4 结语(1) 运用改进节点虚流量法,针对不同的降排水方案和降水参数,给出了渠道工程的渗流场分布、抽水量和渠底地下水位。结果表明,在满足工程施工期基坑降排水要求的前提下,单排井点布置可有效降低地下水位,且工程量小、发生渗透破坏的可能性小,对渠道工程降水最为有利。
(2) 降水井的降水效果对降水井纵向间距的选择十分敏感,降水井纵向间距越小(即降水井布置越密集),抽水量越小,降水效果越好。因此,实际工程中,应谨慎合理地选择降水井的纵向间距。
(3) 合理选择降水井的抽水水位对施工期降排水工程尤为重要。当降水井布置不变,加深降水井抽水水位可显著提高单井抽水量,降低渠底的地下水位。抽水水位过小或过大均不能满足施工期对基坑降水的需求,因此,应合理选择降水井抽水水位对施工期基坑进行降水,并尽量均匀对称地布置井管,使工程达到既经济又合理的降水效果。在本文渠道工程中,当降水井抽水深度为-6 m时,各方案降水效果均满足干地施工要求,达到了既经济又合理的降排水效果。
(4) 降水井布置越密集,纵向间距越小,单井发生渗透破坏的可能性就越小。同样的渗控措施下,降水井边界处的水力坡降对潜水位的变化极为敏感,左右临空面的潜水位越高,降水井边界就越容易发生渗透破坏。所以在工程前期准备过程中应加强对地下水位的勘测。
| [1] |
祁书文. 基于有限元法的复杂三维渗流场计算方法研究[D]. 南京: 河海大学, 2007. (QI Shuwen. Research on calculation method of seepage discharge for complicated 3D seepage flow field based on FEM[D]. Nanjing: Hohai University, 2007. (in Chinese))
|
| [2] |
RASTOGI A K, PRASAD B. FEM modelling to investigate seepage losses from the lined Nadiad branch canal, India[J]. Journal of Hydrology, 1992, 138(1-2): 153-168. DOI:10.1016/0022-1694(92)90162-O |
| [3] |
KANG T. Comparison of seepage analysis methods based on finite elements[C]//Computer Methods and Recent Advances in Geomechanics-Proceedings of the 14th int. Conference of International Association for Computer Methods and Recent Advances in Geomechanics, IACMAG 2014, 2015: 1421-1426.
|
| [4] |
GOYAL R, CHAWLA A S. Seepage from canals with infiltration from free zone surface[J]. Journal of Irrigation and Drainage Engineering, 1997, 123(4): 257-263. DOI:10.1061/(ASCE)0733-9437(1997)123:4(257) |
| [5] |
WANG Hui, GAO Yating, QIN Qinghua, et al. Green's function based finite element formulations for isotropic seepage analysis with free surface[J]. Latin American Journal of Solids and Structures, 2015, 12(10): 1991-2005. DOI:10.1590/1679-78251726 |
| [6] |
李明川, 姚军, 葛家理. 渗流力学进展与前沿[J]. 力学季刊, 2012, 33(1): 74-80. ( LI Mingchuan, YAO Jun, GE Jiali. Research progress and development on seepage mechanics[J]. Chinese Quarterly of Mechanics, 2012, 33(1): 74-80. (in Chinese)) |
| [7] |
李斌, 凌霄, 宋志宇. 南水北调中线一期穿黄工程南岸渠道高边坡渗流分析[J]. 长江科学院院报, 2009, 26(10): 82-86, 91. ( LI Bin, LING Xiao, SONG Zhiyu. Seepage analysis on high slope of Yellow River tunnel project in first-stage of Middle Route South-to-North Water Transfer Project[J]. Journal of Yangtze River Scientific Research Institute, 2009, 26(10): 82-86, 91. DOI:10.3969/j.issn.1001-5485.2009.10.019 (in Chinese)) |
| [8] |
崔皓东, 张家发, 张伟, 等. 南水北调中线典型承压水地层渠段渗流场数值分析[J]. 岩土力学, 2010, 31(增刊2): 447-451. ( CUI Haodong, ZHANG Jiafa, ZHANG Wei, et al. Numerical analysis of seepage field for typical canal stretch on confined aquifer of Middle Route Project of South-to-North Water Transfer[J]. Rock and Soil Mechanics, 2010, 31(Suppl2): 447-451. (in Chinese)) |
| [9] |
王金龙, 张家发, 崔皓东, 等. 南水北调中线典型渠段施工期降水措施研究[J]. 郑州大学学报(工学版), 2012, 33(5): 82-86. ( WANG Jinlong, ZHANG Jiafa, CUI Haodong, et al. Dewatering measures for construction period of the typical canal stretch of Middle Route Project of SNWT[J]. Journal of Zhengzhou University(Engineering Science), 2012, 33(5): 82-86. (in Chinese)) |
| [10] |
崔皓东, 朱岳明. 有自由面渗流分析的改进节点虚流量全域迭代法[J]. 武汉理工大学学报(交通科学与工程版), 2009, 33(2): 238-241. ( CUI Haodong, ZHU Yueming. Improved procedure of nodal virtual flux of global iteration to solve seepage free surface[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2009, 33(2): 238-241. (in Chinese)) |
| [11] |
朱岳明. Darcy渗流量计算的等效结点流量法[J]. 河海大学学报, 1997, 25(4): 105-108. ( ZHU Yueming. Darcy seepage discharge calculation with node method[J]. Journal of Hohai University, 1997, 25(4): 105-108. (in Chinese)) |
| [12] |
王新敏. ANSYS工程结构数值分析[S]. 北京: 人民交通出版社, 2007. (WANG Xinmin. Numerical analysis of engineering structure with ANSYS[S]. Beijing: China Communication Press, 2007. (in Chinese))
|
| [13] |
钟登华, 张晓昕, 敖雪菲, 等. 复杂渠道工程三维渗流应力耦合分析与研究[J]. 中国科学(技术科学), 2013, 43(11): 1993-1201. ( ZHONG Denghua, ZHANG Xiaoxin, AO Xuefei, et al. Study on coupled 3D seepage and stress fields of the complex channel project[J]. Science China (Techologica Sciences), 2013, 43(11): 1993-1201. (in Chinese)) |
| [14] |
毛昶熙. 渗流计算分析与控制[M]. 北京: 中国水利水电出版社, 2003. ( MAO Changxi. Seepage computation analysis and control[M]. Beijing: China Water and Power Press, 2003. (in Chinese))
|
| [15] |
贺武斌, 崔向东, 刘彦忠. 基坑开挖及降水井间距对其周围环境影响的模拟研究[J]. 太原理工大学学报, 2013, 44(3): 381-384. ( HE Wubin, CUI Xiangdong, LIU Yanzhong. Simulation research on surrounding environment influenced by pit excavation and dewatering well spacing[J]. Journal of Taiyuan University of Technology, 2013, 44(3): 381-384. (in Chinese)) |
| [16] |
孙蓉琳, 梁杏, 张晓伦, 等. 数值模拟技术在基坑降水中的应用[J]. 岩土力学与工程学报, 2003, 22: 2333-2337. ( SUN Ronglin, LIANG Xing, ZHANG Xiaolun, et al. Application of numerical modeling to dewatering design for foundation pit[J]. Chinese Journal of Rock Mechanics and Engeering, 2003, 22(Suppl1): 2333-2337. (in Chinese)) |
2. School of Water Conservancy, North China University of Water Resources and Electric Power, Zhengzhou 450045, China
 2017
2017 