2. 重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074
三峡水库蓄水后,长江上游航道等级得以提升,库区内的船舶数量以及吨位都在不断增大,不但加大了航道内的通航密度,也加大了锚地船舶的密度。由于地质条件原因,三峡库区滑坡事故频发,滑坡体入水会形成巨大涌浪,极易造成锚泊船舶走锚甚至锚链断裂,造成巨大经济损失和人员伤亡。为了减少滑坡涌浪对锚泊船舶的损害,需要对涌浪作用下锚泊船舶锚链拉力进行研究,从而确保锚泊船舶的安全。
国内外主要采用理论分析和经验分析的方法对锚链及受力情况进行研究。日本的滨村建治[1]提出悬垂曲线计算法, 考虑各种外力, 求出锚链长度, 改善了船舶的锚泊性能。Huang[2]运用质量集中弹簧模型与有限元法,提出了一种预报三维锚链张力的数值方法。Shashikala等[3]应用有限元法研究了波浪与单点系泊驳船干扰的三维问题,研究了锚链刚度系数对不同系泊点驳船的影响。Gobat等[4]提出了悬链型锚链上端因垂向运动引起的动张力的计算模型,可以计算锚链张力的标准方差。Sasa等[5]对单点锚泊船只在风浪作用下的纵荡、横荡和艏艉摇进行了数值模拟,重点分析其走锚情况。白辅中[6]分析研究了国内外大量的资料,进行了船舶多锚链系泊稳定性的计算。刘应中等[7]在考虑风、浪、流三种荷载同时作用的情况下,采用推广的三维集中质量法求得锚链的动力特性。范菊等[8]应用二阶频域摄动理论计算压载状态下锚泊船舶一阶运动和二阶运动的锚泊线张力谱。刘建成等[9]在考虑风、浪、流三种荷载同时作用的情况下,利用设计谱理论计算油驳的波浪诱导纵荡力。李天匀等[10]采用数值模拟计算方法分析了风浪冲击作用下锚泊渔船锚链的动力负荷。周崇庆等[11]对风浪中锚泊渔船的锚链系泊张力进行了数值模拟分析。侯建军等[12]采用迭代法和优选法求解了3种锚泊状态下锚链对船体的作用力, 为实现完整的锚泊仿真系统提供了重要的理论基础。上述研究都主要着重理论分析和数值模拟计算,不能很好反映真实受力条件,尤其是滑坡这种地质灾害产生的涌浪能量大、危害强,会对船舶锚泊系统造成严重威胁,而锚链又是锚泊系统的核心,为确保锚泊船舶的安全,锚链的受力分析是必不可少的。基于此,本文通过物理模型试验,分析滑坡涌浪作用下锚泊船舶锚链拉力的变化规律,得到锚链最大拉力的经验计算式。
1 模型试验 1.1 河道与滑坡体模型设计试验以万州江南沱口码头河段为原型,为获得原型和模型中物理现象相似,必须满足几何相似、运动相似和动力相似。根据统计资料得到的滑坡体几何尺寸以及试验条件和试验可操作性确定几何比尺为1:70,时间比尺为1:70,力的比尺为1:703。根据1:70的几何比尺将该河段概化为长52 m、宽8 m的弯曲河道。根据岩体滑坡实测资料中几何形态统计,并考虑到试验条件限制和操作的方便性,试验拟定滑坡体长度固定为1 m,通过不同滑体宽厚比控制滑坡体的体积,结合库区滑坡体长宽比统计选取3种不同的宽度和厚度,概化滑坡体几何参数如表 1所示。
| 表 1 概化滑坡体几何参数 Table 1 Geometric parameters of generalized landslide |
通过对库区滑坡区域滑面坡度的资料进行统计,发现滑坡滑面坡度分布在20°~60°,平均为36°,因此滑坡滑面倾角取为20°,40°和60°。
岩质滑坡体由岩石块体和块体之间的空隙和空区组成,因此在结构形式上根据统计资料将滑体进行散体化,对滑坡体采用散体模拟时,确保其密度相似,采用5种不同尺寸但块体长度、宽度和厚度满足1:0.667:0.333比例的矩形块体,经过不同的排列组合来实现滑坡体的离散和裂隙情况的模拟。块体规格如表 2所示。
| 表 2 概化模型滑坡体块体尺寸 Table 2 Size of landslide models |
滑坡体的宽度通过宽度可以变化的铁质滑槽来控制,可变范围为0.5~1.5 m。滑槽底部摩擦系数和滑坡体原型基本相似。
1.2 船舶与锚链模型设计根据几何相似、重力相似和运动相似原则,按1:70的几何比尺设计船舶模型,船舶模型质量、重心位置、吃水、自振周期等均与原型相似。试验船型选择3 000 t甲板驳船,出于工程安全考虑,本次试验设计船舶装载度为满载。实体船和模型船的船型参数如表 3所示。
| 表 3 船舶参数统计 Table 3 Ship parameters |
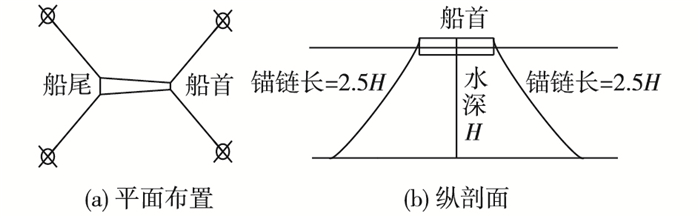
船体采用定位锚泊系统,双侧锚泊方式,船首船尾各两根锚链。根据几何相似、重力相似原则,按照1:70的几何比尺设计船舶锚链。试验选取船型为3 000T,根据海港工程设计手册[13]中锚泊船舶锚链强度和锚链抛出长度的规定模拟原型船舶锚链链径为d=40 mm,根据几何相似原理选取锚链链径为0.5 mm,根据重力相似原理锚链在重力作用下为悬链线状态。因重力比尺为1,密度比尺为1,因此选用不锈钢链。本次试验主要研究船舶受涌浪影响发生橫摇旋转等运动时锚链从悬链状态到紧绷状态受力情况,因此试验锚链悬链线设计可以满足锚链受力相似。从安全角度出发,考虑不利状态下系泊方式,锚链长度取为水深的2.5倍。两根锚链夹角取90°,锚链与船中轴线夹角为45°。具体布置如图 1所示。
|
图 1 船舶锚链平面布置及纵剖面 Figure 1 Layout plan and profile of ship anchor |
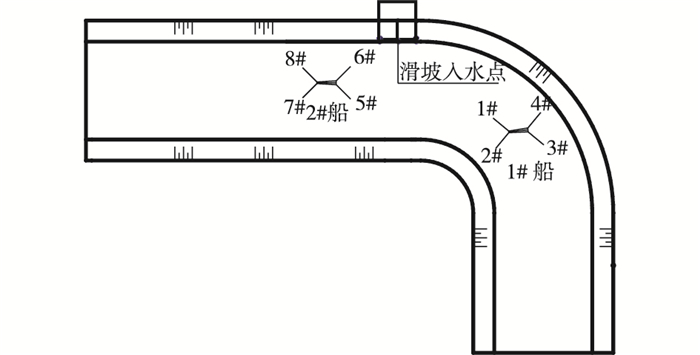
根据实际依托工程为弯曲河道的特点分别在滑坡体附近河道弯道段及直道段处布置锚泊船舶1#船舶和2#船舶,船舶距离滑坡入水点分别为5和9 m,且两只船舶走向均平行于直道段河岸,见图 2。
|
图 2 锚泊船舶平面布置 Figure 2 Layout plan of anchored vessel |
三峡库区正常蓄水位为175 m,枯水期消落水位为155 m,汛期防洪限制水位为145 m。结合实际地形,按照1:70的几何比尺计算试验水位,结果分别为1.16, 0.88和0.74 m。通过统计分析库区滑坡体产状资料,选择滑坡体宽度、厚度、滑面倾角3个因素进行滑坡体产状设计。最终试验设计为四因素三水平完全试验共81组试验方案。影响因素设计如表 4所示。
| 表 4 影响因素设计 Table 4 Design of factors and levels |
试验波高测量采用重庆西南水运工程科学研究所自主研发的UBL-2型超声波浪采集分析仪,采集时间为200 s,采集频率为50 Hz。船舶锚链拉力由型号为CYG1145的拉力传感器测量,传感器量程为6 kPa,测量精度为0.5级。拉力采集系统精度为100 Hz。高清摄像机拍摄船舶运动状态。
2 试验成果分析 2.1 锚链拉力随涌浪传播的变化规律根据试验现场观察和录像分析发现,在涌浪的作用下,锚泊船舶会产生偏荡(横荡、垂荡、橫摇)和扭转,当船舶偏移达到一定距离或者扭转达到一定角度时,一侧锚链迅速拉紧,在锚链拉力作用下船舶反向偏移或扭转。又因船舶为双侧锚泊,在涌浪和锚链共同作用下,船舶不断往复运动。
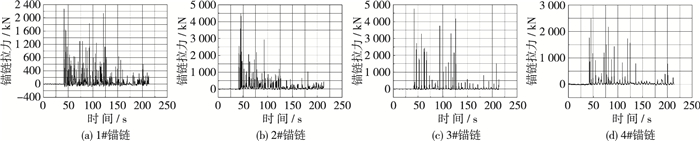
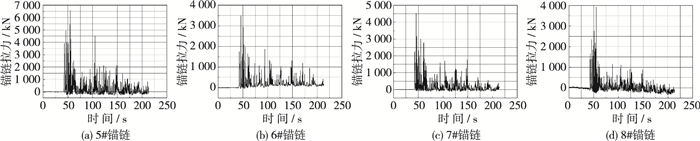
经过分析所有工况锚链拉力的变化,发现船舶锚链拉力的变化和大小具有相同规律。选取滑坡体宽度1.5 m,厚度0.6 m,滑面倾角40°,水深为0.88 m的工况,绘制涌浪作用下弯道段锚泊船舶锚链(1#~4#)和直道段锚泊船舶锚链(5#~8#)拉力随时间变化的过程曲线。锚链拉力大小按照模型比尺反算至原型。锚链编号和位置如表 5所示。船舶锚链拉力随时间变化过程如图 3和4所示。
| 表 5 锚链编号位置 Table 5 Anchor number and position |
|
图 3 弯道段船舶锚链拉力时域图 Figure 3 Time domain chart in curved section of ship mooring force |
|
图 4 直道段船舶锚链拉力时域图 Figure 4 Time domain chart in straight section of ship mooring force |
(1) 锚链拉力测量值均为脉冲值,弯道段船舶锚链拉力的最大值为首个或者第2个脉冲值,随着时间的推移和涌浪的衰减,脉冲值整体呈现衰减趋势,但在整个衰减过程中会出现几个数值和最大值相差不大的脉冲值,这是因为弯道段涌浪的反射叠加情况复杂不断出现大波。直道段船舶锚链拉力的最大值出现在多个震荡周期之后,随后随着涌浪的衰减,脉冲值逐渐减小。这是因为在滑坡体附近经过反射叠加的波浪比初始涌浪更大。
(2) 弯道段船舶1#和3#锚链拉力变化规律相同,2#和4#锚链拉力变化相同。直道段船舶5#和8#锚链拉力变化规律相同,6#和7#锚链拉力变化相同。这是由于船舶锚泊走向和滑坡入水点位置原因,涌浪大约呈45°入射角作用于船舶,使得船舶发生扭转和推移,所以锚链拉力的变化规律以船舶中心位置对称出现。
(3) 弯道段船舶2#锚链拉力最大值大于1#锚链,3#锚链拉力最大值大于4#锚链,直道段船舶5#锚链拉力最大值大于8#锚链,7#锚链拉力最大值大于6#锚链,即船舶左侧锚链拉力大于船舶右侧锚链拉力。
根据相关研究[14],船舶锚链拉力的变化规律和船舶的橫摇角度变化密切相关,为了验证本文锚链拉力变化规律的准确性,运用高清摄像机拍摄滑坡体入水后,船舶由静止到橫摇再到静止的全过程,将每一帧的录像提取出来,运用相关软件进行处理得到橫摇角度随时间的变化规律,如图 5所示。
|
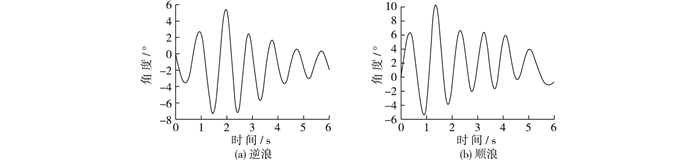
图 5 船舶橫摇角度时域图 Figure 5 Time domain diagram of ship roll angle |
图 5中正值为船舶重心向顺浪方向倾斜,负值为朝逆浪方向倾斜。由图 5可见船舶橫摇最大角度不是在第1个波峰处出现,而是第2或者第3个波峰处出现,随后船舶最大橫摇角度逐渐衰减直至平稳,这一现象和船舶锚链最大拉力的变化规律一致,证明了上述船舶锚链拉力变化规律的正确性。
2.2 锚链拉力变化规律影响船舶锚链拉力的因素很多,如船舶类型、船舶自振周期、锚链抛出长度、锚链抛出角度、波浪入射角度、波高、波周期、航道水深等。本次试验确定船舶类型为3 000T甲板驳船,船舶橫摇固有周期11.5 s、横荡固有周期13.5 s,锚链抛出长度为水深的2.5倍,锚链抛出角度约为45°,波浪入射角度约为45°。基于此本文主要研究波高、波周期和航道水深对船舶锚链拉力的影响。因为船舶锚链拉力变化规律以船舶中心对称,再加上船舶左侧锚链拉力大于船舶右侧锚链拉力,因此只研究2#,3#,5#和7#锚链拉力的变化规律。
2.2.1 锚链拉力随初始波高的变化根据模型比尺反算至原型,选取波高范围1.5~14 m之间的18组工况,绘制弯道段和直道段锚泊船舶2#,3#,5#和7#测点锚链拉力受初始波高影响的变化曲线,如图 6所示。
|
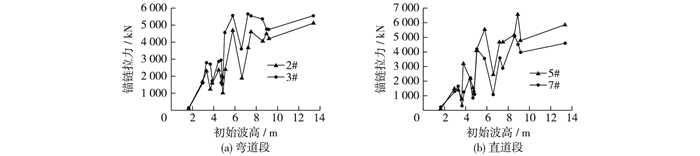
图 6 弯道段和直道段船舶锚链拉力随波高变化 Figure 6 Changes of ship mooring force of straight section and curved section with wave height variation |
由图 6可以看出弯道段和直道段船舶锚链拉力随波高变化的规律基本一致,锚链拉力整体随波高增大波动上升。初始波高在5~7 m时,锚链拉力突变比较明显,5 ~6 m锚链拉力急剧上升,6~7 m之间拉力急剧下降;当初始波高达到10 m后,锚链拉力增幅变小。随着波高的增大,波能不断增加,船舶受到的作用力不断增大,船舶发生扭转和偏移的幅度不断增大,在往复运动中锚链拉力不断增大。由此可知初始涌浪波高对锚泊船舶锚链拉力大小起决定性作用。
2.2.2 锚链拉力随波浪周期的变化规律选取周期为5 ~25 s的18组工况,绘制弯道段和直道段锚泊船舶2#,3#,5#和7#测点锚链拉力受波浪周期影响的变化曲线,如图 7所示。
|
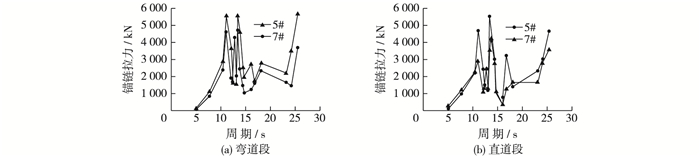
图 7 船舶锚链拉力随波浪周期变化 Figure 7 Changes of ship mooring force of straight section and curved section with wave period variation |
由图 7可以看出弯道段和直道段船舶锚链拉力随波浪周期变化的规律基本一致,从整体上看锚链拉力随波浪周期的增大呈现周期性变化。波浪周期为5.0~11.0 s时,锚链拉力急剧增大。在11.0 ~15.0 s时,锚链拉力具有较大突变,11.0 ~12.5 s时拉力迅速下降,12.5~13.5 s拉力迅速增大,13.5 ~15.0 s拉力又迅速下降,之后波动比较平缓,在波浪周期为23 s时锚链拉力又急剧增大。锚泊船舶受涌浪作用会发生横荡、垂荡和橫摇。当涌浪周期和锚泊船舶横荡、垂荡及横摇运动的固有自振周期相同或接近时,就会发生谐摇运动,船舶的运动量由于共振就会大幅度增加,从而导致锚链拉力急剧增加。
2.2.3 锚链拉力随水深的变化规律选取滑坡体宽度、高度、滑面倾角相同,模型水位分别为0.74, 0.88和1.16 m(按照模型比尺换算至原型为145, 155和175 m)的3组工况,绘制弯道段和直道段锚泊船舶2#,3#,5#和7#测点锚链拉力受水深影响的变化曲线,如图 8所示。
|
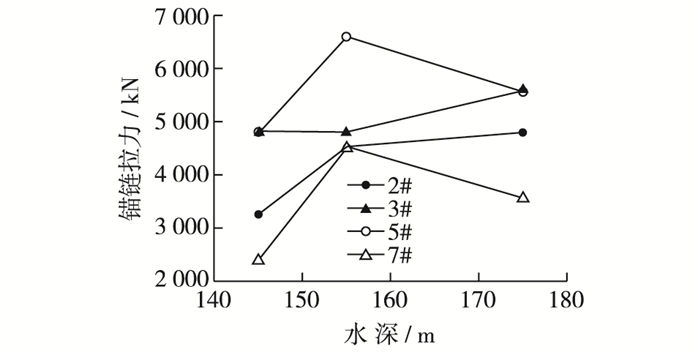
图 8 船舶锚链拉力随水深变化 Figure 8 Changes of ship mooring force with wave depth variation |
由图 8可见, 在三峡库区正常水位运行下,随着水位的提高,船舶锚链拉力没有一个确切的变化规律。但是可以发现直道段船舶锚链拉力受水位变化影响程度比弯道段要大。
2.3 滑坡涌浪作用下船舶最大锚链拉力的回归分析经过上述分析得知,弯道段和直道段锚泊船舶最大锚链拉力变化规律基本一致,因此可以用一个计算式表达。船舶锚链最大拉力受初始波高H、涌浪周期T、库区水深h的影响。经过无量纲分析得:
| $ F/(\rho {h^4}/{T^2}) = f(H/h, {T^2}g/h) $ | (1) |
采用线性函数、幂函数、指数函数进行多元线性回归可以得到如下3个船舶最大锚链拉力的经验公式。
| $ F/(\rho {h^4}/{T^2}) = 0.017{\rm{ }}77\left( {H/h} \right) + 0.000{\rm{ }}1({T^2}g/h) - 0.000{\rm{ }}73 $ | (2) |
| $ F/(\rho {h^4}/{T^2}) = 0.001{\rm{ }}5{\left( {H/h} \right)^{1.158{\rm{ }}21}}{({T^2}g/h)^{1.429{\rm{ }}66}} $ | (3) |
| $ F/(\rho {h^4}/{T^2}) = 0.000{\rm{ }}046\text{exp}(48.422{\rm{ }}68\left( {H/h} \right) + 0.100{\rm{ }}37({T^2}g/h)) $ | (4) |
式中: F为船舶最大锚链拉力(kN);T为涌浪周期(s);H为涌浪初始波高(m);h为水深(m);ρ为水密度,取1 000 kg/m3;g为当地重力加速度,取9.8 m/s2。
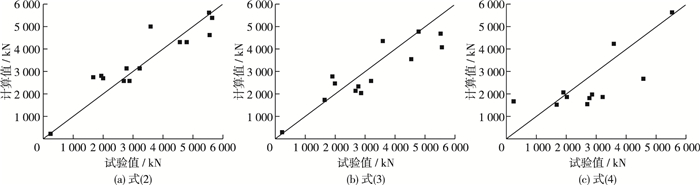
运用上述3个计算式计算船舶锚链最大拉力值并与试验值进行对比(见图 9)。
|
图 9 船舶锚链最大拉力计算值与试验值对比 Figure 9 Comparison between calculation values and test results of the maximum ship mooring force |
由图 9可见,各点均匀分布在直线y=x两侧,说明计算值和试验值比较吻合,其中式(3)吻合程度最高,且拟合式相关系数为0.96,基于此本文建议采用式(3)计算滑坡涌浪作用下锚泊船舶最大锚链拉力。
为验证上述计算式结果是否合理,与天津水运科学研究所李焱[15]的锚链最大拉力计算式进行对比分析。李焱提出的计算式为
| $ F = 523{H^{1.256}} $ | (5) |
式中: F为船舶锚链拉力(kN);H为波浪波高(m)。
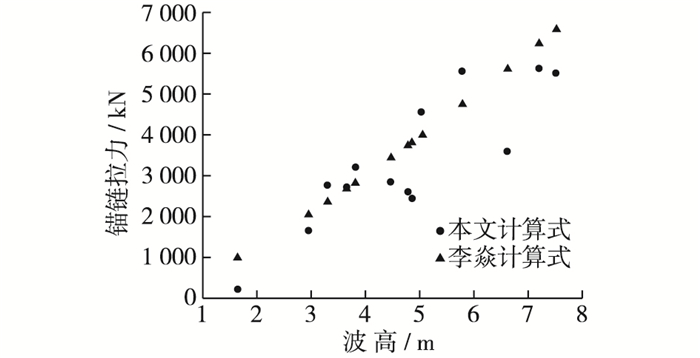
对比结果如图 10所示。由图 10可以看出,本文计算所得的船舶最大锚链拉力计算的结果和天津水运科学研究所李焱计算式的结果基本吻合,证明了本文试验计算式的可靠性。
|
图 10 不同计算式数据对比 Figure 10 Data comparison between different formulas |
采用水槽概化模型试验研究了滑坡涌浪对三峡库区锚泊船舶最大锚链拉力的影响,主要研究结论如下:
(1) 锚链拉力测量值均为脉冲值,弯道段船舶锚链拉力的最大值为首个或者第2个脉冲值,直道段船舶锚链拉力的最大值出现在多个震荡周期之后。随着时间的推移和涌浪的衰减,脉冲值整体呈现衰减趋势,但在弯道段锚链拉力整个衰减过程中会出现几个数值和最大值相差不大的脉冲值。
(2) 当涌浪大约呈45°入射角作用于船舶时,锚链拉力的变化规律以船舶中心位置对称;且船舶远离滑坡入水点一侧锚链拉力要大于近滑坡入水点一侧。
(3) 锚链拉力整体随涌浪初始波高增大而增大。当涌浪周期和锚泊船舶横荡、垂荡及横摇运动的固有自振周期相同或接近时,锚链拉力急剧增加。直道段船舶锚链拉力受水位变化影响程度比弯道段要大。
(4) 通过多元回归分析得到了滑坡涌浪作用下锚泊船舶最大锚链拉力计算的经验式。
由于试验条件限制,本次试验没有考虑船舶自振周期、锚链抛出长度、锚链抛出角度、波浪入射角度等因素的影响,为了更加精确有效地研究滑坡涌浪对船舶最大锚链拉力的影响,建议可从以上几个方面进一步加强研究。
| [1] |
滨村建治, 余昭允. 锚链曲线和锚链抛出长度[J]. 船舶, 1993(3): 54-58. ( HAMAMURA K, YU Zhaoyun. The chain length curve and shackles[J]. Ships, 1993(3): 54-58. (in Chinese)) |
| [2] |
HUANG S. Dynamic analysis of three-dimensional marine cables[J]. Ocean Engineering, 1994, 21(6): 587-605. DOI:10.1016/0029-8018(94)90008-6 |
| [3] |
SHASHIKALA A P, SUNDARAVADIVELU R, GANAPATHY C. Dynamics of a moored barge under regular and random waves[J]. Ocean Engineering, 1997, 24(5): 401-430. DOI:10.1016/S0029-8018(96)00019-4 |
| [4] |
GOBAT J I, GROSENBAUGH M A. A simple model for heave-induced dynamic tension in catenary moorings[J]. Applied Ocean Research, 2001, 23(3): 159-174. DOI:10.1016/S0141-1187(01)00013-X |
| [5] |
SASA K, INCECIK A. Numerical simulation of anchored ship motions due to wave and wind forces for enhanced safety in offshore harbor refuge[J]. Ocean Engineering, 2012, 44(2): 68-78. |
| [6] |
白辅中. 船舶多锚链系泊稳定性计算[J]. 河海大学学报(自然科学版), 1993, 21(2): 21-27. ( BAI Fuzhong. Stability calculation of multi-anchor chain system[J]. Journal of Hehai University(Natural Science Edition), 1993, 21(2): 21-27. (in Chinese)) |
| [7] |
刘应中, 缪国平, 李谊乐, 等. 系泊系统动力分析的时域方法[J]. 上海交通大学学报, 1997, 31(11): 7-12. ( LIU Yingzhong, MIAO Guoping, LI Yile, et al. A time domain computation method for dynamic behavior of mooring system[J]. Journal of Shanghai Jiaotong University, 1997, 31(11): 7-12. (in Chinese)) |
| [8] |
范菊, 黄祥鹿. 锚泊线的动力分析[J]. 中国造船, 1999(1): 13-20. ( FAN Ju, HUANG Xianglu. The analysis of mooring line dynamics[J]. Chinese Ship Building, 1999(1): 13-20. (in Chinese)) |
| [9] |
刘建成, 李润培, 顾永宁, 等. 一种简易单点系泊系统的可行性研究[J]. 上海交通大学学报, 2000, 34(1): 132-136. ( LIU Jiancheng, LI Runpei, GU Yongning, et al. Study on the feasibility of a simple single point mooring system[J]. Journal of Shanghai Jiaotong University, 2000, 34(1): 132-136. (in Chinese)) |
| [10] |
李天匀, 周崇庆, 刘土光, 等. 风浪冲击下锚泊渔船的锚链动力负荷[J]. 华中理工大学学报, 1998, 26(9): 97-99. ( LI Tianyun, ZHOU Chongqing, LIU Tuguang, et al. The dynamic force acted on the chain cable of mooring fishing ships in the wind and the waves[J]. Journal of Huazhong University of Science and Technology, 1998, 26(9): 97-99. (in Chinese)) |
| [11] |
周崇庆, 刘土光, 李天匀. 风浪中锚泊渔船的锚链系泊张力的分析研究[J]. 中国水产科学, 1999, 6(3): 78-80. ( ZHOU Chongqing, LIU Tuguang, LI Tianyun. Analysis of chain tension for fishing vessel anchoring in rough water[J]. Journal of Fishery Science of China, 1999, 6(3): 78-80. (in Chinese)) |
| [12] |
侯建军, 东昉, 石爱国, 等. 锚泊状态下锚链作用力的计算方法[J]. 大连海事大学学报, 2005, 31(4): 10-14. ( HOU Jianjun, DONG Fang, SHI Aiguo, et al. Calculation method of chain force on ship at anchor[J]. Journal of Dalian Maritime University, 2005, 31(4): 10-14. (in Chinese)) |
| [13] |
交通部第一航务工程勘察设计院. 海港工程设计手册(中)[S]. 北京: 人民交通出版社, 1994. (The First Survey and Design Institute of the Ministry of Transportation. Navigational engineering port engineering design manual (middle)[S]. Beijing: China Communications Press, 1994.(in Chinese))
|
| [14] |
孙一艳, 王刚, 陈国强, 等. 风浪流作用下单船艏艉锚泊允许波高的试验研究[J]. 水运工程, 2015(11): 25-29. ( SUN Yiyan, WANG Gang, CHEN Guoqiang, et al. Stern mooring of a single ship under combined action of wind, wave and current[J]. Port and Waterway Engineering, 2015(11): 25-29. DOI:10.3969/j.issn.1002-4972.2015.11.005 (in Chinese)) |
| [15] |
李焱, 肖辉, 李松喆, 等. "开"型浮箱式防波堤运动特性和锚链力试验[J]. 水道港口, 2015, 36(6): 474-480. ( LI Yan, XIAO Hui, LI Songzhe, et al. Experimental study on motions and mooring forces of开-type pontoon floating breakwater[J]. Journal of Waterway and Harbour, 2015, 36(6): 474-480. (in Chinese)) |
2. National Engineering Research Center for Inland Waterway Regulation, Chongqing Jiaotong University, Chongqing 400074, China
 2017
2017 
