我国大量通航河流处于西部山区峡谷地带,通常河势狭窄、落差大、流量及水位变幅显著[1]。为了适应经济和内河航运的迅速发展,我国通航船闸的尺度及水头亦逐渐增大,正在向多线巨型化发展,目前国内已建总水头30 m以上的高水头船闸有长江三峡、闽江水口、沅水五强溪、赣江万安、潇水双牌、攸水酒埠江、乌江银盘等[2-5]。高水头大尺寸船闸建设将面临输水、消能、阀门防空化等一系列技术难题,采用合适的输水系统布置和闸室消能措施来消杀水体中的巨大能量,确保闸室、引航道内船舶安全以及船闸自身的运行安全,同时兼顾输水效率等均对船闸输水系统设计提出了极高的要求[6-7],必须开展严谨的论证和分析研究。
大藤峡水利枢纽工程是一座以防洪、航运、发电、水资源配置为主,结合灌溉等综合利用的大型水利枢纽工程。其船闸采用单线单级,闸室有效尺度为280 m×34 m×5.8 m(有效长度×有效宽度×门槛水深),设计最大水头为40.25 m,正常运行输水时间要求小于15 min。大藤峡水利枢纽工程船闸设计水头高、规模大,一次充泄水量达42万m3,是目前国内已建单级船闸之最[8-9],其输水系统设计方案拟采用四区段八分支廊道盖板消能方案,如图 1所示。

|
图 1 大藤峡船闸输水系统布置 Figure 1 Layout of filling and emptying system of Datengxia lock |
大藤峡船闸输水系统第二分流口设置在闸室长度1/4及3/4处,初步设计拟采用空腔自分流型式,使船闸充、泄水水流在第二分流口空腔内部顶冲、碰撞,进而自行分流至4根分支廊道中去,属于被动强迫分流,国内尚无类似工程实例;然而第二分流口作为输水系统的关键局部结构,其输水过程中的水力特性直接影响船闸输水安全及效率,决定了船闸是否能够正常运行,因此本文通过采用三维数值模拟的技术手段对最大设计水头阀门双边开启工况下该分流口型式及输水系统的整体分流性能进行研究,分析各典型充、泄水时刻第二分流口的输水水力特性,论证其在工程实际应用中的可行性。
1 数学模型建立计算流体动力学(Computational Fluid Dynamics,简称CFD)立足于流体运动的基本方程,采用数值分析的方法模拟流场中若干离散点的物理量,获得详细水力特性指标,是研究流体流动问题的重要手段之一[10-13],本文通过建立三维紊流数学模型对第二分流口自分流体型的输水水力特性开展研究,具体如下。
1.1 水流控制方程组任何水流流动问题都必须满足质量守恒定律,该定律可表述为:单位时间内流体微元体中质量的增加与相同时间间隔内流入该微元体的净质量相等。根据这一定律可得出质量守恒方程,如式(1)所示。
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho u} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho v} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho w} \right)}}{{\partial z}} = 0 $ | (1) |
式中:ρ为流体密度;t为时间;u, v, w为速度矢量在x,y,z方向上的分量。
动量守恒定律也是任何流动系统都必须满足的基本定律,不可压缩流体的动量方程见式2(a)~2(c):
| $ \frac{{\partial \left( {\rho u} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho uu} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho uv} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho uw} \right)}}{{\partial z}} = {S_x} - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial u}}{{\partial z}}} \right) $ | (2(a)) |
| $ \frac{{\partial \left( {\rho v} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho vu} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho vv} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho vw} \right)}}{{\partial z}} = {S_y} - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial u}}{{\partial z}}} \right) $ | (2(b)) |
| $ \frac{{\partial \left( {\rho w} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho wu} \right)}}{{\partial x}} + \frac{{\partial \left( {\rho wv} \right)}}{{\partial y}} + \frac{{\partial \left( {\rho ww} \right)}}{{\partial z}} = {S_z} - \frac{{\partial p}}{{\partial x}} + \frac{\partial }{{\partial x}}\left( {\mu \frac{{\partial u}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {\mu \frac{{\partial u}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {\mu \frac{{\partial u}}{{\partial z}}} \right) $ | (2(c)) |
式中:μ为动力黏度系数;p为压力;Sx, Sy, Sz分别为3个坐标轴方向上的动量源项。
1.2 紊流模型船闸充、泄水过程中第二分流口及各分支廊道存在水流顶冲、对撞、支孔射流等复杂水流流态,综合考虑计算要求、精度和计算时间,选取重整化群k-ε模型(RNG k-ε模型)对Navier-Stokes控制方程进行封闭。重整化群k-ε模型是针对标准k-ε模型在模拟强旋流或带有弯曲壁面的流动时出现失真现象而提出的,在模拟冲击射流、分离流、二次流等复杂流动时具有较大的优势,模型中湍动能k方程和耗散率ε的输运方程表达式为:
| $ \frac{{\partial \left( {\rho k} \right)}}{{\partial t}} + \frac{{\partial (pk{u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _k}{\mu _{{\rm{eff}}}}\frac{{\partial k}}{{\partial {x_j}}}} \right] + {G_{\rm{k}}} + {G_{\rm{b}}} - \rho \varepsilon - {Y_{\rm{M}}} $ | (3) |
| $ \frac{{\partial \left( {\rho \varepsilon } \right)}}{{\partial t}} + \frac{{\partial (p\varepsilon {u_i})}}{{\partial {x_i}}} = \frac{\partial }{{\partial {x_j}}}\left[{{\alpha _\varepsilon }{\mu _{{\rm{eff}}}}\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + {C_{1\varepsilon }}\frac{\varepsilon }{k}({G_{\rm{k}}} + {C_{3\varepsilon }}{G_{\rm{b}}}) - {C_{2\varepsilon }}\rho \frac{{{\varepsilon ^2}}}{k} - R $ | (4) |
式中:μeff=μ+μt;αk和αε分别为湍动能k和耗散率ε的有效紊动普朗特数的倒数;Gk为由平均速度梯度引起的紊动动能;Gb为由浮力影响引起的紊动动能;YM为可压缩湍流脉动膨胀对总耗散率的影响;R为耗散附加项;C1ε, C2ε为经验常数;C3ε为表征浮力对紊动耗散影响程度的系数。根据有关学者的试验验证,本研究中各模型经验参数取值如下:Gb=0;YM=0;C1ε=1.42;C2ε=1.68。
1.3 数值计算方法采用有限体积法(FVM)对控制方程进行离散,使每个网格点周围有一个互不重复的控制体积,将待解的微分方程对每个控制体积积分,从而得到一组离散方程。通过将非线性偏微分方程转变为网格单元上的线性代数方程,然后通过求解线性方程组,得到流场的解。对于瞬态问题,PISO算法有明显的优势,本研究中结合实际情况采用PISO算法的迭代计算方法。
1.4 计算区域及定解条件考虑到船闸闸室在整体上呈对称布置,因此在模拟时仅取下半闸室区域进行计算。计算时采用恒定流方法对船闸充、泄水过程中的典型水位-流量节点进行模拟,进而近似获取船闸整个充泄水过程中的水动力特性。图 2为典型工况计算模型的三维立体图,定义沿纵支廊道向下游闸首为X正向、沿闸室高度方向为Y轴正向、闸室横断面为Z向。
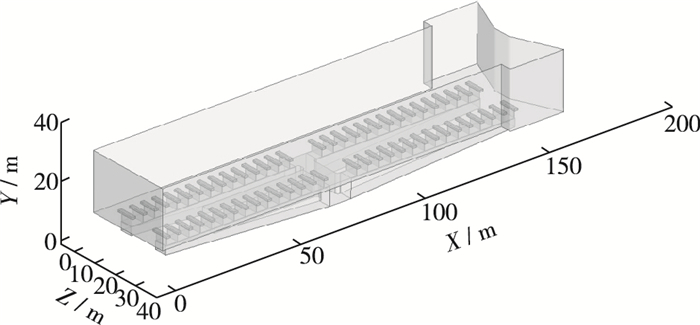
|
图 2 计算区域三维立体图 Figure 2 Three-dimensional graph of computational domain |
闸室充水和泄水两种截然不同运行工况的计算边界条件如下:对于充水工况,取底部纵支廊道横断面为进口边界,采用速度入口,并给定边界口上的紊动能k和紊动耗散率ε的估算值;闸室上部为自由液面,采用压力出口边界;闸室及廊道的壁面采用无滑移边界条件,对于近壁区域,采用标准壁面函数法进行模拟;对于泄水工况,闸室上部自由液面为进口边界,设置为压力进口,纵支廊道末端横断面为出口边界,采用速度出口,壁面及近壁区域的模拟与充水工况相同。
在计算中,各方程的最小残差值设为1×10-5,即当计算残差值小于最小残差值时迭代结束。
1.5 网格划分由于模型采用盖板消能,且存在数量较多的出水支孔,结构形状较为复杂,因此三维计算网格采用非结构化网格和结构化网格相结合的方式。在计算区域内,闸室上部区域结构简单,采用结构网格划分;而对于廊道、分流口及出水支孔等区域采用非结构网格划分;在研究重点区域及体型变化较大的局部区域如分流口、出水支孔处进行网格加密,如图 3所示。计算网格总数根据计算工况的不同略有差异,总体在300万左右。
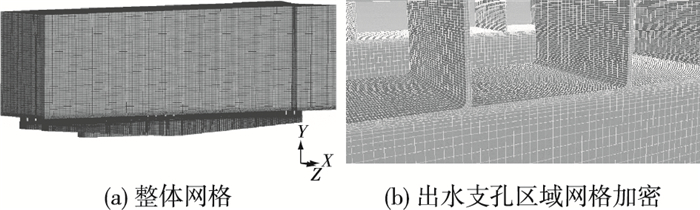
|
图 3 模型网格划分 Figure 3 Mesh partition |
采用大藤峡船闸输水系统第二分流口局部物理模型试验结果对数学模型的准确性进行验证,由于试验中较难测得输水廊道及分流口内部各部位的精确流速指标,本文选取阀门6 min开启双边充水工况下分流口同一部位的时均压力指标进行对比(见表 1),其中Q为典型时刻的流量,H为对应水位。
| 表 1 典型测点压力特性对比验证 Table 1 Comparison of the pressure characteristics of typical measuring points |
由表 1可知,数模计算结果与物理模型试验结果稍有差异,分析产生部分差异的原因主要有:①数学模型在边界设置以及近壁区域水流模拟方面存在一定假设,与模型试验有一定差别;②分流口内部水流紊动较强,试验测点存在相对较大的压力脉动。尽管如此,从整体上看计算所得压力与物理模型试验测得结果基本一致,所建数学模型具有可靠的模拟精度。
2 结果分析与讨论本文通过数值模拟研究,获取了大藤峡船闸输水系统第二分流口内部水流流动特性、压力分布特征等,并对各分支廊道以及出水支孔的出流量进行统计,定量分析了输水系统整体分流均匀性,为进一步验证该分流口型式在高水头船闸输水系统布置中的合理可行性提供技术参考。
2.1 充水工况水力特性分析 2.1.1 流场分布特征输水系统内流速大小及分布是衡量分流口布置方案是否可行的重要指标,对于大藤峡水利枢纽船闸工程,设计推荐充水阀门开启时间为6 min,因此本文针对tv=6 min充水工况进行数值模拟,图 4为典型充水计算工况第二分流口及输水廊道三维流场结构,图 5为设计方案推荐阀门开启时间tv=6 min不同水位-流量时刻分流口区域的水平剖面流场结构,从中可以看出:①整体上看,分流口内部呈现三维复杂流场结构,流态较为紊乱,不同工况下分流口内部整体水流结构较为相似;②船闸充水过程中,分流口与闸底纵支廊道相接部位即入口弯道侧壁附近将会出现最大流速,在阀门6 min开启、最大流量时计算所得分流口区域最大流速为12.34 m/s;③充水时分流口内部的水流顶冲面中心区域会出现小范围低流速紊动区,水流经强烈碰撞向两侧分流后在下游分支廊道弯段处形成大流速区域,而上游分支廊道拐弯处则流速较小;④分流口与四分支廊道连接段的边壁区域由于水流向上下廊道分流同样会形成小范围不稳定低流速区。

|
图 4 第二分流口及部分输水廊道三维流场(充水) Figure 4 3D flow field of second diversion port and part of conveyance culvert (water filling condition) |

|
图 5 不同水位-流量工况下第二分流口水平剖面流场分布(单位:m/s) Figure 5 Flow field distribution in the horizontal section under the condition of different water levels and flow rates (unit: m/s) |
在船闸充水过程中,第二分流口内部压力场不断变化,图 6以两组计算工况为例展示了分流口内部的典型压力分布。
由图 6可以看出:①充水过程中,第二分流口内部压力场结构较为紊乱,但存在明显的区域分布特征;②水流的顶冲作用使得大墩头壁面上存在较大范围高压区;在分流口与四分支廊道交接处靠下游侧由于水流的直接冲击作用亦会形成较高压力区域;分流口入口弯段以及下游分支廊道弯段侧壁处则会形成低压区;③船闸充水不同时刻,第二分流口内部压力分布基本相同,压力的大小与闸室水位及充水流量有关。

|
图 6 不同水位-流量工况下第二分流口水平剖面压力分布(单位:Pa) Figure 6 Pressure distribution in the horizontal section under the condition of different water levels and flow rates (unit: Pa) |
一个合理的分流口布置型式需保证输水廊道内水流分流均匀稳定,为方便表述,将大藤峡船闸输水系统各分支廊道及出水支孔编号如图 7所示,在设计方案中1#~4#分支廊道的出水孔总面积分别为10.00,9.25,10.00和9.25 m2。数模中对tv=6 min不同流量级工况下4根分支廊道以及各出水支孔的出流量进行统计,见图 8~9,从图中可以看出:①通过调整出水支孔尺寸,各分支廊道分流量虽然存在细微差异,但在各流量级工况下差异不大,整体上分流较为均匀;②同一根分支廊道上,各出水支孔的流量亦存在一定的不均衡现象,然而从船闸整体输水效果上来看,可认为第二分流口在充水工况下分流较为均匀、稳定,基本满足分流要求。
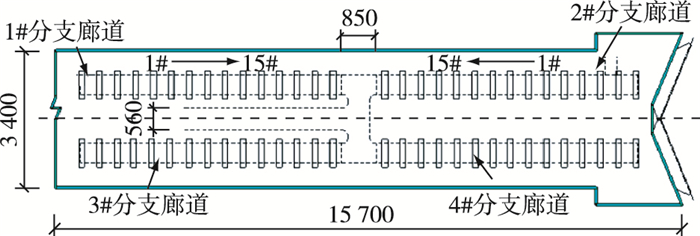
|
图 7 各分支廊道及出水支孔编号设置(单位:cm) Figure 7 Number setting of each branch corridor and outlet hole (unit: cm) |
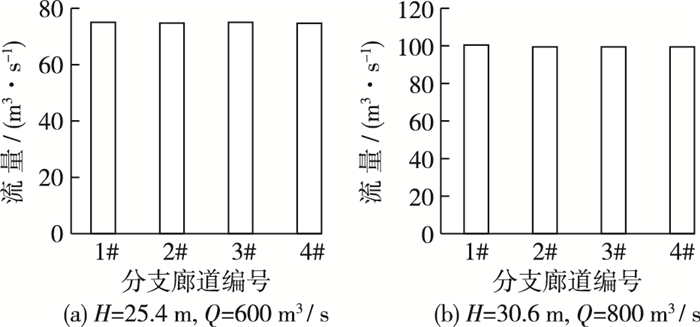
|
图 8 不同充水工况下各分支廊道流量对比 Figure 8 Comparison of flow rate of each corridor under different water filling conditions |

|
图 9 不同充水工况下各出水支孔流量对比 Figure 9 Comparison of flow rate of each outlet hole under different water filling conditions |
大藤峡水利枢纽船闸工程设计推荐泄水阀门开启时间为2 min,因此本研究着重针对tv=2 min泄水工况开展数值模拟,图 10为典型泄水计算工况下,第二分流口及输水廊道的三维流场结构,图 11为设计方案推荐阀门开启时间tv=2 min不同时刻第二分流口水平剖面的流场结构,可见:①整体上看,分流口内部流场结构较为复杂,泄水过程中,闸室水流由出水支孔流入各分支廊道,然后在分流口空腔内顶冲碰撞,最终汇入闸底纵支廊道,呈现较为复杂的三维流场结构;②船闸泄水过程中,分流口与闸底纵支廊道相交接的弯道侧壁附近将出现最大流速,在tv=2 min、最大流量时,数模计算分流口区域最大流速可达12.97 m/s;③泄水时四股水流在分流口内部交汇,将在分流口内部侧壁中心区域形成较大范围的不稳定三角紊动区,结合以往研究经验分析可知,该区域在水流条件变化或其他扰动作用下,可能会产生随机突发的水流扫略、脉动等不稳定现象,对工程结构造成影响,需予以关注;在分流口与四分支廊道连接段的侧壁区域由于水流对撞泄流,同样会形成不稳定低流速区;④不同数模计算工况下分流口内部整体水流结构较为相似,均存在代表性的流速分布区域。
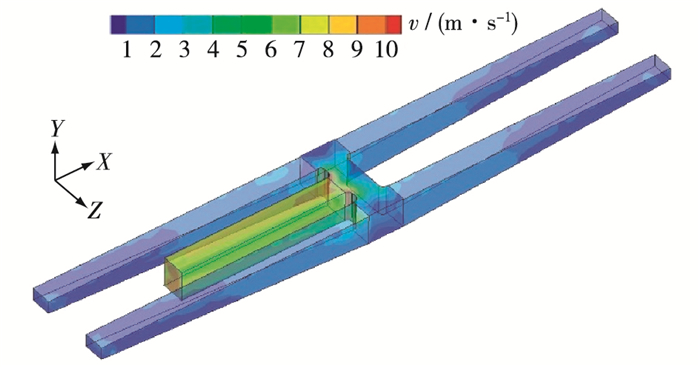
|
图 10 第二分流口及部分输水廊道三维流场(泄水) Figure 10 3-D flow field of second diversion port and part of conveyance culvert (water emptying condition) |

|
图 11 不同水位-流量工况下第二分流口水平剖面流场分布(单位:m/s) Figure 11 Flow field distribution in the horizontal section under the condition of different water levels and flow rates (unit: m/s) |
在船闸泄水过程中,第二分流口内部压力场亦不断变化,图 12为不同工况下分流口内部的典型压力分布。从图 12可以看出:①泄水过程中,第二分流口内部压力场结构较为紊乱,但同样存在明显的区域分布特征;②船闸泄水过程中,分流口内部各拐弯侧壁区域均会形成低压分布,最小压力值出现在分流口与闸底纵支廊道交接处,同时纵支廊道整体压力较各分支廊道要小;③分流口内部在垂直方向上的压力分布基本为沿深度逐渐增加,但从整体上看其顶部靠近中心区域压力相对较小;④不同泄水工况下,第二分流口内部压力场结构基本相同,压力大小与闸室水位和流量密切相关。

|
图 12 不同水位-流量工况下第二分流口压力分布(单位:Pa) Figure 12 Pressure distribution under different water levels and flow rates (unit: Pa) |
图 13为不同泄水工况下各分支廊道分流量对比,可以看出,在船闸泄水时,第二分流口各分支廊道的出流量略有不均;将分支廊道各出水支孔的流量对比绘制如图 14所示,可见由于各出水支孔有效孔径不同,其出流量也存在不均衡的现象,但是从船闸整体输水均匀性上来看,第二分流口在泄水工况下基本能够满足分流要求。
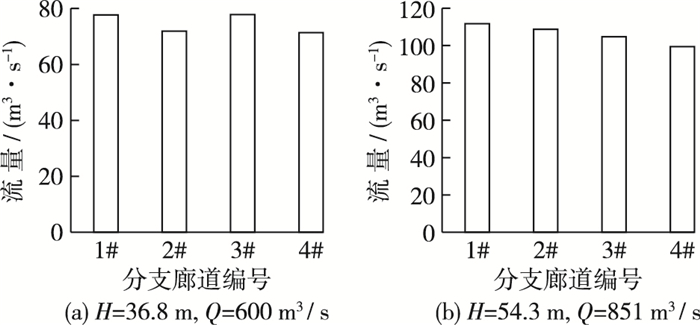
|
图 13 不同泄水工况下各分支廊道分流量对比 Figure 13 Comparison of flow rate of each corridor under different water release conditions |
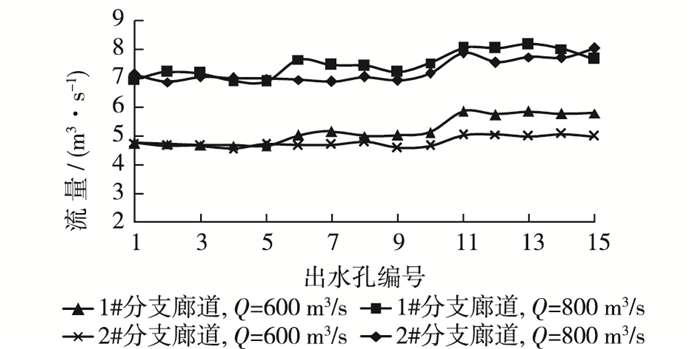
|
图 14 不同泄水工况下各出水支孔流量对比 Figure 14 Comparison of flow rate of each outlet hole under different water release conditions |
分流口作为输水系统的关键局部结构,对船闸输水安全和输水效率影响甚大,特别是在高水头船闸中,由于输水能量大,水力指标高,其分流口结构设计需予以重点关注。本文以大藤峡水利枢纽工程船闸输水系统拟采用的第二分流口型式为例,通过采用三维数值模拟的技术手段,对其输水水力特性进行了细致研究,得出以下结论:
(1) 通过在设计方案中对分支廊道出水支孔尺寸和布置进行合理调整,第二分流口采用空腔自分流体型能够满足船闸充、泄水运行的分流要求,分流较为均匀。
(2) 船闸充、泄水运行时,该分流口体型内部呈现复杂的三维流场结构,并存在典型的流速、压力分布区域,尤其在泄水工况下分流口内部侧壁中心区域(大墩头中心)会形成较为明显的大范围低流速、相对低压三角区域,结合以往研究经验分析可知,该区域在水流条件变化或其他扰动作用下,可能会产生随机突发的水流扫略、脉动等不稳定现象,对工程结构造成影响,需予以关注。
(3) 研究获取了大藤峡船闸输水系统第二分流口内部水流流动特性、压力分布特征等,但数学模型在边界及近壁区流动模拟上不可避免地存在一定简化,下阶段需在数模研究基础上对该分流口体型的输水水力特性开展进一步的专项试验研究,确保工程安全高效运行。
| [1] |
熊治平. 河流概论[M]. 北京: 中国水利水电出版社, 2011. ( XIONG Zhiping. An introduction to rivers[M]. Beijing: China Water & Power Press, 2011. (in Chinese))
|
| [2] |
涂启明. 考察五强溪、万安、水口船闸[C]//通航论文集, 1999: 267-271. (TU Qiming. Investigation of Wuqiangxi, Wan'an and Shuikou lock[C]//The Third Symposium of the Navigation Specialized Committee of CSHE, 1999: 267-271. (in Chinese))
|
| [3] |
钮新强, 童迪. 三峡船闸关键技术研究[J]. 水力发电学报, 2009, 28(6): 36-42. ( NIU Xinqiang, TONG Di. Research on the key technologies of Three Gorges shiplocks[J]. Journal of Hydroelectric Engineering, 2009, 28(6): 36-42. (in Chinese)) |
| [4] |
宣国祥, 李云, 胡亚安, 等. 西部超高水头枢纽通航建筑物关键技术研究[R]. 南京: 南京水利科学研究院, 2007. (XUAN Guoxiang, LI Yun, HU Ya'an, et al. Research on key technologies of navigation structures under the super high water head of western China[R]. Nanjing: Nanjing Hydraulic Research Institute, 2007. (in Chinese))
|
| [5] |
陈明栋, 杨忠超, 杨斌, 等. 乌江银盘船闸输水系统选型研究[J]. 重庆建筑大学学报, 2006, 28(5): 30-34. ( CHEN Mingdong, YANG Zhongchao, YANG bin, et al. Studies on the type selection of the filling and emptying system of Yingpan lock on Wujiang River[J]. Journal of Chongqing Jianzhu University, 2006, 28(5): 30-34. (in Chinese)) |
| [6] |
李君, 宣国祥, 黄岳, 等. 等惯性两区段分散输水系统在40 m级单级巨型船闸中的应用[J]. 水运工程, 2016(12): 20-25. ( LI Jun, XUAN Guoxiang, HUANG Yue, et al. Application of two-section four-manifold total-balanced filling and emptying system in 40 m-grade single-step giant ship lock[J]. Port & Waterway Engineering, 2016(12): 20-25. DOI:10.3969/j.issn.1002-4972.2016.12.003 (in Chinese)) |
| [7] |
宣国祥, 刘本芹, 李君, 等. 船闸输水系统水力学创新技术研究和实践[R]. 南京: 南京水利科学研究院, 2009. (XUAN Guoxiang, LIU Benqin, LI Jun, et al. Research and practice on hydraulic innovation technology of lock filling and emptying system[R]. Nanjing: Nanjing Hydraulic Research Institute, 2009. (in Chinese))
|
| [8] |
覃业传, 宣国祥, 麦建清, 等. 大藤峡水利枢纽单级船闸输水系统初步分析[J]. 水利水运工程学报, 2012(4): 71-76. ( QIN Yechuan, XUAN Guoxiang, MAI Jianqing, et al. Feasibility analysis of the filling and emptying system for Datengxia high head single-step shiplock[J]. Hydro-Science and Engineering, 2012(4): 71-76. (in Chinese)) |
| [9] |
程玉姣, 李亚文, 常万军, 等. 大藤峡水利枢纽工程船闸位置选择[J]. 东北水利水电, 2016, 34(7): 3-4. ( CHENG Yujiao, LI Yawen, CHANG Wanjun, et al. The location selection of ship lock in Datengxia hydraulic project[J]. Water Resources & Hydropower of Northeast China, 2016, 34(7): 3-4. (in Chinese)) |
| [10] |
王福军. 计算流体动力学分析: CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004. ( WANG Fujun. Computational fluid dynamics: Principles and applications of CFD software[M]. Beijing: Tsinghua University Press, 2004. (in Chinese))
|
| [11] |
ANDERSONJ D. 计算流体力学基础及其应用[M]. 北京: 机械工业出版社, 2007. ( ANDERSON J D. Computational fluid dynamics[M]. Beijing: China Machine Press, 2007. (in Chinese))
|
| [12] |
韩占忠, 王敬, 兰小平. Fluent—流体工程仿真计算实例与应用[M]. 北京: 北京理工大学出版社, 2010. ( HAN Zhanzhong, WANG Jing, LAN Xiaoping. Fluent-fluid engineering simulation and its application[M]. Beijing: Beijing Institute of Technology Press, 2010. (in Chinese))
|
| [13] |
STOCKSTILL R L, BERGER R C. A three-dimensional numerical model for flow in a lock filling system[C]//ASCE: World Environmental and Water Resources Congress, 2009: 1-10.
|
 2017
2017 