2. 福建省水利水电勘测设计研究院,福建 福州 350001
随着能源危机和环境污染问题的加剧,海上风电开发和利用受到世界各国的广泛关注。按照国家能源局“十二五”规划,到2015年底,海上风电装机容量不低于500万kW,2020年将不低于3 000万kW[1]。与常规海洋平台、桥梁等不同,海上风机整体结构的允许频率偏低,往往因与风机叶片振动频率一致,引发共振现象[2]。在风、波浪、地震等随机动载作用下,为避免风电基础发生脆性破坏,除了满足静力承载要求,还需要考虑动力方面的影响。早期国内外学者对陆上风机的振动特性进行了研究,近几年开始逐步转向海上风电领域。郇彩云等[3]采用土弹簧考虑桩土相互作用对塔筒和基础振动的影响;胡国玉等[4]研究海上风电桨叶的振动特性;何叶等[5]考虑周期性波浪荷载作用研究塔筒与基础的动力响应。上述研究均具有局限性,海上风电的桨叶、塔筒与基础的尺寸较大,所处环境复杂且基础形式多样化,简化的方式不利于风机振动特性的准确评估。本文在前人研究的基础上,建立海上风电“地基-基础-塔筒-机舱-桨叶”整体耦联结构有限元模型,研究风机整体振动特性,同时考虑不同基础形式与不同基础约束方式的影响,为桩筒复合基础的设计与后期的动力分析提供借鉴。
1 海上风电有限元模型 1.1 模型及材料参数风机塔筒高75 m,直径为2.7~5.0 m;桨叶选用玻璃钢材料,长50 m,宽3.6~2.2 m。本文选取天津大学近几年研发的新型基础形式——桩筒复合基础[6],该基础由桩、筒、支撑板、混凝土灌浆四部分组成,尺寸如下:桩基础直径5 m,总长度45 m,厚度60 mm,其中泥面以下长30 m,桩顶部通过法兰环与上部结构连接;筒基础直径16 m,内部开洞直径5.2 m,筒壁高度为3 m,顶盖和筒裙所用钢板厚度为60 mm;在筒基础顶盖均匀布置6个横向肋板,肋板在筒体内侧高度为3 m,外侧高度为0.5 m,肋板厚度为30 mm;单桩基础和筒型基础之间灌注厚度为10 cm的高强灌浆材料。所用材料参数如表 1所示。
| 表 1 材料参数 Table 1 Material parameters |
采用湘电XE128-5000型风机,切入风速3 m/s,切出风速25 m/s,风机转速范围为8.5~16.5 rpm,对应的1P(马达转动频率)范围为0.142~0.275 Hz,3P(风机叶轮扫掠频率)范围为0.425~0.825 Hz[7]。基于现有的波浪资料,本工程重现期2年一遇至100年一遇的波浪周期为6.0~11.4 s,相应的波浪波动频率为0.088~0.167 Hz。风、地震主频频率为0.01~0.10 Hz和1.00~10.00 Hz[8]。
1.2 模型建立在进行网格划分时,上部结构、土体与基础统一采用C3D8R单元。上部结构连接处采用tie连接。为了消除土体有限边界对模型计算的不利影响,本文选用圆柱形土体,土体直径为100 m,高度为80 m,土体尺寸足够大,可忽略边界效应的影响。土体底部进行固结约束,侧面约束径向位移与转角,风机整体模型如图 1所示。

|
图 1 风机整体有限元模型 Figure 1 Finite element model of overall wind turbine |
模态分析用于分析结构固有特性,确定结构的自振频率和固有振型。假设风电整体为线弹性体,并处于小变形范围内。由平衡方程、物理方程和几何方程可导出结构的有限元基本方程[7-8]:
| $ \mathit{\boldsymbol{M\ddot{u}}}\rm{+}\mathit{\boldsymbol{C\dot{u}}}\rm{+}\mathit{\boldsymbol{Ku}}\rm{=}\mathit{\boldsymbol{F}}\left( \mathit{t} \right) $ | (1) |
式中:M为总体质量矩阵;C为总体阻尼矩阵;K为总体刚度矩阵;F(t)为结构所受外力矩阵;
求解时忽略阻尼的影响,结构有限元离散化处理后,应用瞬时最小势能原理,可得到结构的无阻尼自由振动方程:
| $ \mathit{\boldsymbol{M\ddot{u}}}\rm{+}\mathit{\boldsymbol{Ku}}\rm{=0} $ | (2) |
无阻尼模态分析求解基本方程是经典的特征值问题:
| $ \mathit{\boldsymbol{K}}{{\mathit{\boldsymbol{ \varphi}}\rm{ }}_{\mathit{i}}}\rm{=}\mathit{\boldsymbol{ \omega}}\rm{ }_{\mathit{i}}^{2}\mathit{\boldsymbol{M}}{{\mathit{\boldsymbol{ \varphi}}\rm{ }}_{\mathit{i}}} $ | (3) |
式中:φi为第i阶模态振型向量;ωi为第i阶模态的固有频率。
2.2 基础类型与共振约束由风引起的海上风电机组所受动力荷载的激励频率,通过风机转速来体现,即常说的1P(马达转动频率)和3P(风机叶轮扫掠频率)。由于风机的启动转速和退出转速存在转速分布范围,即1P和3P存在分布范围,因此风机基础设计应进行模态分析,使得风机体系的自振频率避开1P和3P的频率分布带。根据自振频率与1P和3P的分布关系,存在3种设计形式:“柔-柔”(频率小于1P)、“柔-刚”(频率大于1P且小于3P)、“刚-刚”(频率大于3P),柔-柔基础如悬浮式基础,易出现严重的疲劳损伤,柔-刚基础如三脚架、导管架等基础,刚-刚基础如重力式基础等。基础整体刚度越大,工程量越大,工程造价也增大[9]。
为避免风电机组整体结构共振,根据德国GL规范要求,激励荷载的频率与风机整体结构的自振频率差别应在5%以上[10]。
| $ \frac{{{\mathit{f}}_{\rm{R}}}}{{{\mathit{f}}_{\rm{0, }\mathit{n}}}}\le \rm{0}\rm{.95或}\frac{{{\mathit{f}}_{\rm{R}}}}{{{\mathit{f}}_{\rm{0, }\mathit{n}}}}\ge \rm{1}\rm{.05} $ | (4) |
式中:fR为激励荷载频率;f0, n为第n阶结构固有频率。
当不满足要求时,一方面调整基础设计方案,另一方面在风电机组中装配振动监控设备。
2.3 动力分析判别假设风机结构为线弹性单自由度体系,在外激励作用下做简谐振动,通过研究谐振反应振幅与静位移比值,即可得出所研究体系是否需要进行动力分析[11]。
| $ \mathit{D}\rm{=}\frac{\mathit{\rho }}{{{\mathit{p}}_{\rm{0}}}\rm{/}\mathit{k}}\rm{=}{{\left[{{\left( \rm{1-}{{\mathit{\beta }}^{\rm{2}}} \right)}^{\rm{2}}}\rm{+}{{\left( \rm{2}\mathit{\varepsilon \beta } \right)}^{\rm{2}}} \right]}^{\rm{-1/2}}} $ | (5) |
式中:D为动力放大系数;ρ为谐振反应振幅;p0为外部激励荷载;k为结构刚度;β=ϖ/ω,ϖ为荷载频率;ω为固有自由振动频率;ε为阻尼比,取0.05。
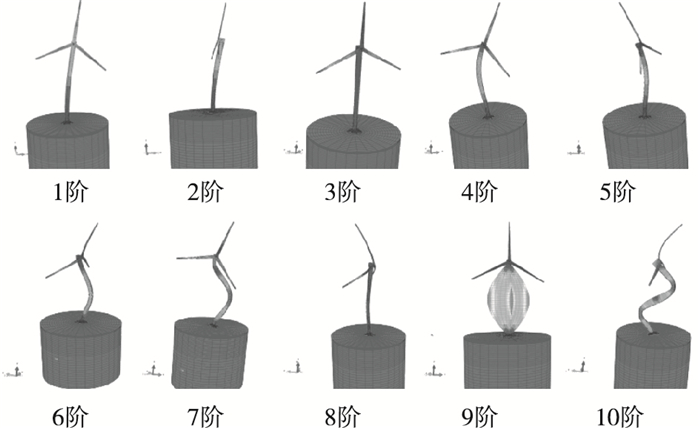
3 计算结果及分析 3.1 频率与振型选用ABAQUS中Block Lanczos方法对风电整体进行模态分析。前10阶模态振型如图 2所示,前10阶模态频率与振型特征如表 2所示。
|
图 2 前10阶模态振型 Figure 2 Modal shapes of top 10 orders |
| 表 2 前10阶模态分析结果 Table 2 Modal analysis of top 10 orders |
本模型在x,y,z三个方向的振型参与质量分别为98.6%,98.3%,95.5%,符合《公路桥梁抗震设计细则》(JTG/TB02-01—2008)[12]规定振型参与质量要达到结构总质量90%的要求,所提取的模态阶数能够充分表现风机整体振动特征。
从表 2可见前2阶频率位于1P和3P范围之间,该基础属于柔-刚基础。风机整体振型前3阶主要是桨叶和机舱的振动,第4阶开始塔筒出现明显的振动,基础振动从第6阶开始,因此,机舱与桨叶的振动是海上风机系统的主要低阶振动,也是造成风机疲劳损伤的主要原因之一[13-14]。同时,桩筒复合基础对风机整体的振动影响不可忽略。
3.2 共振与动力分析判别为验证风机整体是否满足避免共振的条件,计算前3阶频率与激励频率的比值,结果如表 3所示。
| 表 3 风机频率与激励频率的对比 Table 3 Comparison of turbine frequency and excitation frequency |
从表 3可见:风机整体前3阶频率满足式(4)的要求,在该设计条件下,风电机组能够避免共振的发生。在此条件下,对风叶旋转、波浪、风、地震作用下的动力放大系数计算,结果如表 4所示。从表 4可见:当叶片旋转、风荷载波浪达到上限频率与下限频率时,风机整体的动力放大系数均大于1,须进行动力计算;在地震作用下,动力放大系数均小于1,可以对风机作拟静力计算[10]。
| 表 4 动力放大系数计算结果 Table 4 Calculation results of dynamic magnification factor |
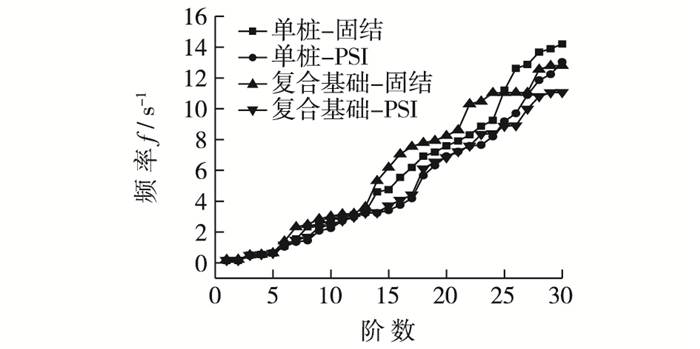
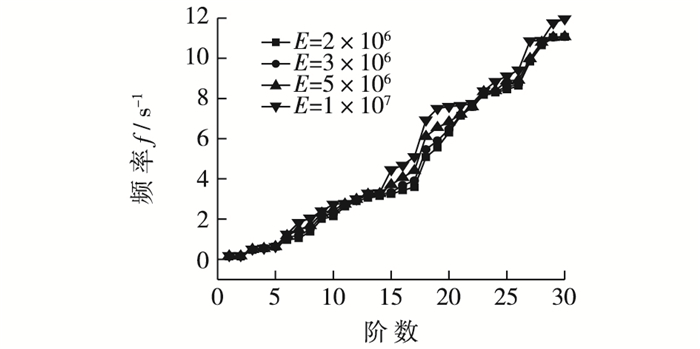
为研究基础类型与不同约束条件对风电整体振动的影响,分别在单桩基础与桩筒复合基础两种基础形式下,取不同约束条件下的前30阶频率进行研究。不同基础和约束条件下风机整体频率见图 3,不同土体弹性模量下风机整体频率见图 4。
|
图 3 不同基础与约束条件下风机整体频率 Figure 3 Frequency of overall turbines in different bases and constraint conditions |
|
图 4 不同土体弹性模量下风机整体频率 Figure 4 Frequency of overall turbines in different elastic modulus |
由图 3可见,当风机采用复合基础时,整体频率高于采用单桩基础的频率,平均高出27.8%,这是因为筒型基础的存在增加了基础的横向约束,进而增大了基础刚度,提高了海上风机承受水平荷载的能力。无论是复合基础还是单桩基础,考虑PSI效应的整体频率要比常规基础底部固结低,说明PSI效应增加了基础约束的柔度,在实际动态分析中需要加以考虑土的作用。
由图 4可以看出不同土体弹性模量的条件下,风机整体的前5阶频率相差不大,随着阶数的增加,频率差距逐步增大,第20阶频率最大相差17.3%。在考虑PSI情况下,随着地基弹性模量的增加,土体刚度增大,风机整体频率增加,因此对于不同土质条件下风机整体振动特性,必要情况下应具体分析。
4 结语(1) 海上风机进行模态分析时,前2阶水平弯曲频率与第3阶扭转频率为判断风机整体共振的主要频率。
(2) 风机振动形式主要为上部结构的振动,叶片以摆动和扭动为主,塔筒以摆动为主,下部基础的振动在前6阶不明显。
(3) 桩筒复合基础属于柔-刚基础,所用设计尺寸能够避免风机共振的发生,且与单桩基础相比,采用桩筒复合基础的海上风电整体刚度更大。
(4) 桩土相互作用会使风机整体柔度增加,振动频率降低,基础设计时需考虑桩土相互作用的影响。
(5) 除地震之外的动载作用下,风机整体均需进行动力计算。
| [1] |
周光召. 2020年中国科学和技术发展研究[M]. 北京: 中国科学技术出版社, 2004. ( ZHOU Guangzhao. Research on the development of science and technology in China in 2020[M]. Beijing: Science and Technology of China Press, 2004. (in Chinese))
|
| [2] |
单光坤, 姚兴佳. 兆瓦级风力发电机组的模态分析[J]. 沈阳工业大学学报, 2008, 30(3): 276-279. ( SHAN Guangkun, YAO Xingjia. Mode analysis on MW grade wind turbine[J]. Journal of Shenyang University of Technology, 2008, 30(3): 276-279. (in Chinese)) |
| [3] |
郇彩云, 姜贞强, 罗金平. 桩土相互作用模拟方法对海上风机整体结构模态分析的影响[J]. 水电能源科学, 2013, 31(1): 236-239. ( XUN Caiyun, JIANG Zhenqiang, LUO Jinping. Influence of interaction between pile and soil on the model analysis of offshore wind turbine[J]. Hydropower and Energy Science, 2013, 31(1): 236-239. (in Chinese)) |
| [4] |
胡国玉, 孙文磊, 金阿芳. 大型风力发电机旋转叶片结构动力特性分析[J]. 可再生能源, 2015, 33(11): 1652-1657. ( HU Guoyu, SUN Wenlei, JIN Afang. The structural dynamic behavior analysis of large scale wind turbine rotational blade[J]. Renewable Energy Resource, 2015, 33(11): 1652-1657. (in Chinese)) |
| [5] |
何叶, 赵明阶, 胡丹妮. 海上风机三桩基础与上部结构动力响应分析[J]. 水利水运工程学报, 2016(2): 17-23. ( HE Ye, ZHAO Mingjie, HU Danni. Dynamic response analysis of tripod pile foundation and superstructure of offshore wind turbine[J]. Hydro-Science and Engineering, 2016(2): 17-23. (in Chinese)) |
| [6] |
天津大学. 一种海上风电机组地基组合基础: 201110324026. 8[P]. 2012-05-09. (Tianjin University. A foundation for offshore wind turbines: 201110324026.8[P]. 2012-05-09.(in Chinese))
|
| [7] |
朱东剑. 筒型基础与单桩相结合的新型复合风电基础研究[D]. 天津: 天津大学, 2012. (ZHU Dongjian. Study on a new composite wind power base combined with single pile foundation[D]. Tianjin: Tianjin University, 2012.(in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10056-1013040466.htm
|
| [8] |
王伟, 杨敏. 海上风电机组地基基础设计理论与工程应用[M]. 北京: 中国建筑工业出版社, 2014. ( WANG Wei, YANG Min. Design theory and engineering application of offshore wind turbine foundation[M]. Beijing: China Building Industry Press, 2014. (in Chinese))
|
| [9] |
靳军伟, 杨敏, 王伟, 等. 海上风电机组单桩基础模态及参数敏感性分析[J]. 同济大学学报(自然科学版), 2014, 42(3): 386-372. ( JIN Junwei, YANG Min, WANG Wei, et al. Offshore wind turbine monopile foundation modal and parameter sensitivity analysis[J]. Journal of Tongji University(Natural Science), 2014, 42(3): 386-372. (in Chinese)) |
| [10] |
GL 2005 Guideline for the certification of offshore wind turbines[S].
|
| [11] |
丁明华, 李昕. 海上风机结构不同计算模型的比较研究[J]. 水电能源科学, 2011, 29(10): 49-52. ( DING Minghua, LI Xin. Comparative study on different models of offshore wind turbine structure[J]. Hydropower and Energy Science, 2011, 29(10): 49-52. DOI:10.3969/j.issn.1000-7709.2011.10.015 (in Chinese)) |
| [12] |
JTG/T B02-01—2008公路桥梁抗震设计细则[S]. (JTG/T B02-01—2008 Guildelines for seismic design of highway bridges[S].(in Chinese))
|
| [13] |
刘香, 高振宁, 李海. 兆瓦级风力发电机塔架的模态分析[J]. 工业建筑, 2012, 42(2): 62-65. ( LIU Xiang, GAO Zhenning, LI Hai. Modal analysis of megawatt wind generator tower[J]. Industrial Construction, 2012, 42(2): 62-65. (in Chinese)) |
| [14] |
赵荣珍, 吕刚. 水平轴风力发电机塔架的振动模态分析[J]. 兰州理工大学学报, 2000, 35(2): 33-36. ( ZHAO Rongzhen, LYU Gang. Vibration modal analysis of horizontal axis wind turbine tower[J]. Journal of Lanzhou University of Technology, 2000, 35(2): 33-36. (in Chinese)) |
2. Fujian Provincial Conservancy and Hydropower Survey and Design Institute, Fuzhou 350001, China
 2017
2017 
