2. 南京工业大学,江苏 南京 211816;
3. 东南大学 交通学院,江苏 南京 210018
天然沉积的软黏土一般都具有一定的结构性[1],包括沉积过程中形成的初始结构性和沉积完成后,由于机械、化学和生物等各种因素影响而产生的结构性[2-3]。由于结构性的存在,天然沉积土的压缩性与重塑土有着显著差别。结构性对天然沉积饱和土力学形状的影响与应力历史和初始孔隙率的影响同等重要[1],大量工程实践表明,土的结构性与其工程性状密切相关,近年来天然沉积土的结构性及其对土体力学性质影响的研究受到了广泛关注。
目前关于结构性土力学特性的研究主要集中在宏观和微观两个方面,其中宏观的力学性质是微观结构的表现,如何建立两者之间的桥梁,是一个重要的科学问题[4-6]。随着土微观结构研究的深入,许多学者认为从微观上认识土的结构是结构性定量化研究的重要途径,微观结构性研究方法主要是从微观角度出发,通过室内压汞试验和扫描电镜试验(SEM)等对其微观结构特征及其演变进行定性或定量的研究。王清等[7]通过SEM图像处理技术研究了黏性土微结构中结构单元体的形态、定向性和孔隙特征等定量评价指标。洪振舜等[8-9]通过两组结构性土的扫描电镜试验、压汞试验结合室内固结和高压三轴试验从宏观和微观两个角度对结构性土的屈服特性进行了深入研究,他认为当固结压力超过结构性土的结构屈服压力时,土的结构性完全丧失,表现出与重塑土相同的力学性质。陈嘉欧[10]研究了珠江三角洲黏土的微观结构特征,从黏性土的微观结构与工程加固效果进行了初步探讨。雷华阳等[11]探讨了海积黏土微结构参数与力学强度的关系,随后又从微观角度出发解释了固结曲线上拐点的意义[12],进而研究了次固结系数的变化规律。卢佩霞等[13]用分形理论研究分析了非饱和土的孔隙结构,并建立了其微观结构和宏观力学性质之间的联系。张先伟等[14]根据SEM图像实现了软土微观结构的三维可视化并得到了真实分形维数。王升福等[15]运用分形理论研究了宁波冻融软黏土的微观孔隙特征,并采用容量维数分析了孔体积和孔表面积。以上成果不仅从微观上描述了结构性土的微观特征,而且建立了描述土体微观结构的定量评价指标,这些研究成果对结构性土微宏观特性的进一步研究和结构性土本构模型的建立具有重要的参考价值。
为了对天然沉积硅藻土在不同应力水平下的微观结构进行定量评价,本文在SEM图像的基础上,结合前人的研究成果,探讨了二值化图像在不同固结压力下的分形特征,以及分形维数与固结压力的关系。
1 天然硅藻土的SEM成像特征本文土样在我国浙江省嵊州市以西约6 km硅藻土矿坑中取得,原上覆土层厚约1.8~2.4 m,采用刀具切削而成。由于其刚度非常大,结构性很强,因而刀具和挖土设备对其扰动很小。其主要参数见表 1。Yoshinaka[16]和Tateishi[17]的研究成果也表明,硅藻土具有很强的结构性,它是一种高含水量的土,但是却具有很高的强度和刚度。
| 表 1 硅藻土的主要物理力学参数 Table 1 Index properties of diatomaceous earth |
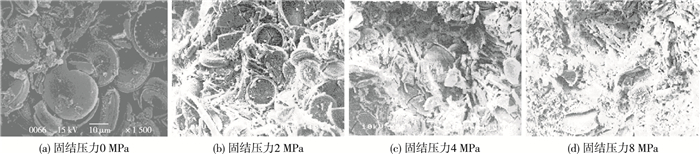
对硅藻土采用高压三轴试验进行各向等压固结,然后进行SEM电镜扫描试验。在进行SEM试样制备时,先将各向等压固结后土样切削成大小约为1 cm3的小块,放入液氮中迅速冷冻1 h,然后在零下50 ℃抽真空干燥,并采用掰断方式形成断口拍摄面,所选取的图像具有较为明显的分形特征,因而具有较强的代表性。图 1为在不同固结压力下,天然沉积硅藻土不扰动样的电镜扫描图像,其中黑色区域为孔隙,白色区域为硅藻颗粒和骨架。由图 1(a)可知,天然硅藻土主要由圆形的硅藻颗粒组成,它们通过外侧的环状物连接在一起而具有很强的结构性。由于这种结构特征,在硅藻颗粒之间和颗粒内部具有很多大小不等的孔隙。HONG等[9]通过压汞试验表明,硅藻土在屈服前孔隙的主要分布区间为0.007~2.0 μm,对应的分布密度存在两个峰值,分别为0.08和1.40 μm,其中0.08 μm主要是由存在于硅藻颗粒内部的孔隙形成,1.4 μm主要是由硅藻颗粒之间的大孔隙骨架导致。由图 1可知当固结压力超过结构屈服压力时,硅藻颗粒破坏,此后随着固结压力增加,大孔隙结构发生坍塌。
|
图 1 天然硅藻土在不同固结压力下的SEM图像 Figure 1 SEM images of natural sedimentary diatomaceous earth under different confining pressures |
表 2为采用压汞试验所得各固结压力下硅藻土的孔隙结构特征参数。王清等[7]根据分形理论,确定黄土的微、小、大孔隙界限,依据0.02和0.800 μm两个孔径划分。雷华阳等[7]提出结构性软土在交通荷载作用下的孔径划分界限为0.01,0.50,2.50 μm。根据前人研究成果,本文结合图 1,将硅藻土孔隙分为:大孔隙,孔径d>10.0 μm;中孔隙,1.0 μm<d≤10.0 μm;小孔隙,0.1 μm<d≤1.0 μm;微孔隙,d≤0.1 μm。按此划分标准将不同固结压力下孔隙分布结果汇于表 2。由表 2可见,硅藻土中孔径为0.1~1.0 μm的孔隙占大部分。
| 表 2 不同固结压力下硅藻土的孔隙结构特征参数 Table 2 Characteristic parameters of pore structure of diatomaceous earth under different consolidation pressures |
在达到屈服压力后,孔径大于1.0 μm的较大孔隙随固结压力的增加而逐渐减少。这一点与SEM图像显示的情况和前述的分析较一致。
2 SEM图像分维数的估算 2.1 数字图像二值化考虑已经存储在计算机内的图像,它是由大小为k*的像素点组成。首先把图像进行二值化处理,使得图像上的每一个像素点为黑或白两种颜色。对本文jpg格式的图片,先用最佳分割阈值的方法对其二值化,得到背景像素为土颗粒(白色)和目标像素为孔隙(黑色)的二值图像。最佳阈值分割法源自图像处理中的分形理论,其基本原理[18]是确定某个灰度阈值,然后判断图像中像素灰度值与阈值的大小关系进行图像分割。采用该法,可以清晰界定物质边界轮廓,将图像转化为黑白两色,有利于后续分析。
在图像进行二值化处理时,当阈值过大时,有时候会将部分土颗粒误认为孔隙,因而须确定最佳阈值,确保大部分土颗粒的轮廓被界定出来。
本文采用如下最佳分割阈值的二值化算法:
(1) 求出图像中最小和最大的灰度值fmin和fmax,将阈值的初始值表示为:
| $ {{\mathit{l}}_{\rm{1}}}\rm{=}\left( {{\mathit{f}}_{\rm{min}}}\rm{+}{{\mathit{f}}_{\rm{max}}} \right)\rm{/2} $ |
(2) 由上一步得出的阈值将数字图像分成前景和背景两部分,求出两部分的平均灰度值f1和f2:
| $ {{\mathit{f}}_{\mathit{A}}}\rm{=}\frac{\sum\limits_{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\mathit{<}{{\mathit{l}}_{\mathit{n}}}}{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\rm{ }\times\rm{ }\mathit{w}\left( \mathit{i}\rm{, }\mathit{j} \right)}}{\sum\limits_{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\mathit{<}{{\mathit{l}}_{\mathit{n}}}}{\mathit{w}\left( \mathit{i}\rm{, }\mathit{j} \right)}} $ | (1) |
| $ {{\mathit{f}}_{\mathit{B}}}\rm{=}\frac{\sum\limits_{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\mathit{>}{{\mathit{l}}_{\mathit{n}}}}{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\rm{ }\times\rm{ }\mathit{w}\left( \mathit{i}\rm{, }\mathit{j} \right)}}{\sum\limits_{\mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\mathit{>}{{\mathit{l}}_{\mathit{n}}}}{\mathit{w}\left( \mathit{i}\rm{, }\mathit{j} \right)}} $ | (2) |
式中:f(i, j)表示平面图像对应的(i, j)点灰度值;w(i, j)表示对应的权重系数,一般取w(i, j)=1。
(3) 求出新的阈值ln+1=(fA+fB)/2,若|ln+1-ln|≤0.001则循环结束,否则,转步骤(2)重新计算。
由上述算法得到固结压力为0,2.0,4.0,8.0 MPa的灰度阈值分别为96,107,101,112。
首先将扫描电镜图像转换为灰度图像,其中灰度较暗区域为孔隙,并分析灰度值,再利用上述算法得到阈值l来提取SEM图像中微观结构信息:
| $ \mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\rm{=}\left\{ \begin{align} & \rm{0}\ \ \ \mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\le \mathit{l} \\ & \rm{1}\ \ \ \mathit{f}\left( \mathit{i}\rm{, }\mathit{j} \right)\mathit{>l} \\ \end{align} \right. $ | (3) |
式中:l为最佳分割阈值算法得到的阈值。采用上述算法处理后的二值化图像如图 2所示。由图 2可知,在固结压力超过结构屈服压力(1.3 MPa)后,硅藻颗粒受到破坏,土体骨架结构发生变化,在外加应力的作用下硅藻颗粒之间的大孔隙逐渐被压缩,内部的孔隙趋于均匀密实。

|
图 2 二值化后的SEM图像 Figure 2 Binary images of SEM |
在Matlab中编写程序,将上述二值化图像转化成对应的数据文件,其行列数分别与二值图的行列数相对应,而每一格数据取值1或0,取决于它所对应的像素点的颜色(如图 2所示),1表示二值化图像中对应的像素点为白色,0表示为黑色。
2.2 数字图像分维数的计算自相似性和分形是许多自然事物和现象的客观特征,存在于自然界中的物理分形往往表现出某种尺度性和随机性,即仅在某种特定的尺度范围内从统计角度上表现出分形特征。如何描述研究对象的分形维数,这取决于研究对象的特征以及研究目的。针对不同的研究对象,可采用不同的描述方法计算其分形维数,如Hausdorff维数和相似维数。然而,对很多分形而言,这两种维数都是难以计算的,在实际计算中我们一般采用盒维数D,它的一种等价计算公式为:
| $ \rm{lg}{{\mathit{N}}_{\mathit{k}}}\rm{=}\mathit{C}\rm{-}\mathit{D}\rm{lg}\mathit{k} $ | (4) |
式中:C为常数;k为盒子的尺寸;Nk表示覆盖所有前景图像需要尺寸为k的盒子数。
在计算时把数据文件划分为若干块,每一块均为正方形,边长包含像素的个数为n,把包含0的块的个数记作Nkn。设一个像素点的尺寸为k*,则行和列都为n的块边长kn=nk*。以kn为边长作为块划分,可以得到对应的盒子数。
据上述计算原理,在双对数坐标平面中,用最小二乘法直线拟合数据点(lg(1/k),lgNk,所得直线的斜率D就是该图像的盒维数。将图 2中的图像带入编制的计算程序,拟合结果如图 3所示,不同固结压力下的Nk值见表 3。

|
图 3 最小二乘法拟合双对数 Figure 3 Linear fitting figure of bi-logarithm coordinates |
| 表 3 不同固结压力下的Nk值 Table 3 Nk in different consolidated pressure |
由图 3可知,不同固结压力下的SEM图像在二值化后具有较好的分形特征。试验数据点与拟合直线的相关性较好。因而可以用分形盒维数描述天然沉积硅藻土在破坏过程中的微观结构变化特征,不同固结压力下分形盒维数如图 4所示。
|
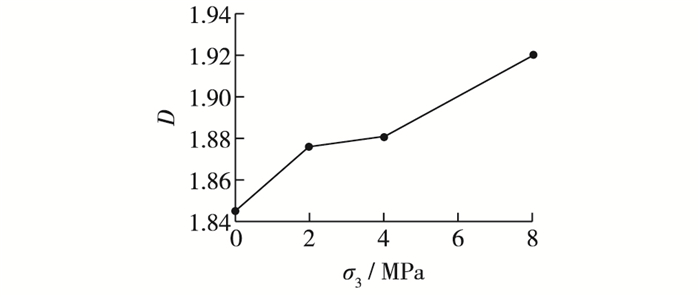
图 4 分形盒维数与固结压力的关系曲线 Figure 4 Relationship between fractal dimension and consolidated pressure |
由图 4可知,分形盒维数随固结压力的增加呈上升的趋势。结合图 1和图 2的SEM图像可将分维的变化分为两个阶段,在压力超过硅藻土的结构屈服压力后,对应的分形维数出现了陡增段,这是由于硅藻颗粒本身破损造成的。此后随着固结压力的增加,分形盒维数也出现了显著的变化,这是由存在于硅藻颗粒间的孔隙结构坍塌所致。因而,对本文讨论的天然沉积硅藻土而言,分形盒维数既可以表征结构性的变化,也可以表征结构性消失后孔隙分布的变化。
3 结语(1) 根据天然硅藻土的SEM成像特征,可知硅藻颗粒为圆形,由外侧环状物连接,土体内部有很多孔隙,具有很强的结构性。由压汞试验可知硅藻土中孔径为0.1~1.0 μm的孔隙占大部分。
(2) 在固结压力达到屈服压力后,孔径大于1.0 μm的较大孔隙随固结压力的增加而逐渐减少,硅藻颗粒破坏,孔隙结构坍塌。并通过由灰度阈值算法得出的二值化图像进一步得到验证。
(3) 在二值化图像的基础上,利用最小二乘法拟合得到了天然沉积硅藻土在不同固结压力下的分形盒子数和盒维数。结果表明分形盒维数随固结压力增加而增加,因此分形特征可反映天然沉积硅藻土在固结压力下的微观结构性及变化。
| [1] |
LEROUEIL S, VAULGHALL P R. The general and congruent effects of structure in natural soils and weak rocks[J]. Geotechnique, 1990, 40(3): 467-488. DOI:10.1680/geot.1990.40.3.467 |
| [2] |
CHANDLER R J. Clay sediments in depositional basin: the geotechnical cycle[J]. The Quarterly Journal of Engineering Geology and Hydrology, 2000, 33(1): 7-39. DOI:10.1144/qjegh.33.1.7 |
| [3] |
COTECCHIA F, CHANDLER R J. A general framework for the mechanical behavior of clays[J]. Geotechnique, 2000, 50(4): 431-447. DOI:10.1680/geot.2000.50.4.431 |
| [4] |
谢定义, 齐吉琳, 张振中. 考虑土结构性的本构关系[J]. 土木工程学报, 2000, 33(4): 35-41. ( XIE Dingyi, QI Jilin, ZHANG Zhenzhong. A constitutive model laws considering soil structural properties[J]. China Civil Engineering Journal, 2000, 33(4): 35-41. (in Chinese)) |
| [5] |
QI Jilin, XIE Dingyi. Soil structure and its quantitative parameter[C]//Proceedings of the Fifteenth International Conference on Soil Mechanics and Geotechnical Engineering. Lisse: Balkema, 2001: 239-242.
|
| [6] |
王国欣, 黄宏伟, 肖树芳. 软土微结构特征的试验研究[J]. 水利学报, 2005, 36(2): 190-196. ( WANG Guoxin, HUANG Hongwei, XIAO Shufang. Experimental study on micro-structural characteristics of soft soil[J]. Journal of Hydraulic Engineering, 2005, 36(2): 190-196. (in Chinese)) |
| [7] |
王清, 王凤艳, 肖树芳. 土微观结构特征的定量研究及其在工程中的应用[J]. 成都理工大学学报, 2001, 28(2): 148-153. ( WANG Qing, WANG Fengyan, XIAO Shufang. A quantitative study of the micro-structure characteristics of soil and its application to the engineering[J]. Journal of Chengdu University of Technology, 2001, 28(2): 148-153. (in Chinese)) |
| [8] |
洪振舜, 立石义孝, 邓永锋. 天然硅藻土的应力水平与孔隙空间分布的关系[J]. 岩土力学, 2004, 25(7): 1023-1026. ( HONG Zhenshun, ITATEISHI Yoshitak, DENG Yongfeng. Relationship between entrance pore distribution and stress level of natural sedimentary diatomaceous soil[J]. Rock and Soil Mechanics, 2004, 25(7): 1023-1026. (in Chinese)) |
| [9] |
HONG Zhenshun, TATEISHI Yoshitak, HAN Jie. Experimental study of Macro-and Micro-behavior of natural diatomite[J]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 2006, 132(5): 603-610. DOI:10.1061/(ASCE)1090-0241(2006)132:5(603) |
| [10] |
陈嘉鸥, 叶斌, 郭素杰, 等. 珠江三角洲软土SEM微结构定量研究[J]. 电子显微学报, 2001, 20(1): 72-75. ( CHEN Jia'ou, YE Bin, GUO Sujie, et al. Quantitative analysis of SEM image of soft ground microstructure in Zhujiang delta[J]. Journal of Chinese Electron Microscopy Society, 2001, 20(1): 72-75. (in Chinese)) |
| [11] |
雷华阳, 肖树芳. 天津海积软土微观结构与工程性质初探[J]. 地质与勘察, 2002, 38(6): 81-85. ( LEI Huayang, XIAO Shufang. Primary exploration on engineering properties of marine soft soil microstructure in Tianjin region[J]. Geology and Prospecting, 2002, 38(6): 81-85. (in Chinese)) |
| [12] |
雷华阳, 肖树芳. 天津软土的次固结变形特性研究[J]. 工程地质学报, 2002, 10(4): 339-343. ( LEI Huayang, XIAO Shufang. Study on secondary-consolidation deformation characteristics of soft soil in Tianjin[J]. Journal of Engineering Geology, 2002, 10(4): 339-343. (in Chinese)) |
| [13] |
卢佩霞, 曹玲, 徐永福. 非饱和土力学的分形理论[J]. 地下空间与工程学报, 2015, 11(2): 375-381. ( LU Peixia, CAO Ling, XU Yongfu. Fractal theory of unsaturated soil mechanics[J]. Chinese Journal of Underground Space and Engineering, 2015, 11(2): 375-381. (in Chinese)) |
| [14] |
张先伟, 王常明, 马栋和. 软土微观结构表面起伏的三维可视化及分形维数的计算[J]. 应用基础与工程科学学报, 2012, 20(1): 104-112. ( ZHANG Xianwei, WANG Changming, MA Donghe. 3D visualization and fractal dimension of soft clay's microstructure surface undulation[J]. Journal of Basic Science and Engineering, 2012, 20(1): 104-112. (in Chinese)) |
| [15] |
王升福, 杨平, 刘贯荣, 等. 人工冻融软黏土微观孔隙变化及分形特性分析[J]. 岩土工程学报, 2016, 38(7): 1254-1261. ( WANG Shengfu, YANG Ping, LIU Guanrong, et al. Micro pore change and fractal characteristics of artificial freeze thaw soft clay[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(7): 1254-1261. (in Chinese)) |
| [16] |
YOSHINAKA R. Mechanical properties for sedimentary soft rocks[M]. Tokyo: Committee of Sedimentary Soft Rocks in Geotechnical Engineering, Japanese Society of Soil Mechanics and Foundation Engineering, 1987: 69-116.
|
| [17] |
TATEISHI Y. Geotechnical properties of diatom earth and stability of surface layer for the cut slope[D]. Saga: Saga University, 1997.(in Japanese)
|
| [18] |
方磊, 李春苗, 龚文忠, 等. 阈值分割法处理土微结构图像质量评价[J]. 地下空间与工程学报, 2013, 9(增刊2): 1045-1049. ( FANG Lei, LI Chunmiao, GONG Wenzong, et al. Quality evaluation of soil micro-structure images processed by thresholding[J]. Chinese Journal of Underground Space and Engineering, 2013, 9(Suppl2): 1045-1049. (in Chinese)) |
2. Nanjing Tech University, Nanjing 211186, China;
3. College of Transportation, Southeast University, Nanjing 210018, China
 2017
2017 