随着碾压混凝土筑坝技术的迅猛发展,各项技术在实际工程中得到了广泛应用。鉴于其分层浇筑和多次碾压的施工特点,导致结构呈现多层特性;碾压层激振力的衰减,致使层内主要物理参数(如弹性模量、抗压强度及密度等)与层深关系密切,部分参数在碾压层内沿层深呈递减或递增的变化规律。与此同时,服役期碾压混凝土坝受荷载、环境等多因素长期协同驱动作用下,随着大坝服役年限的增加及外部环境的变化,筑坝材料与结构出现不同程度的老化及性能时变衰退特性等问题,这些变化致使渗流与应力的相互作用发生改变,坝体在内外环境耦合下产生不利于大坝服役期结构性能的影响效应。
目前,对于碾压混凝土坝的研究,国内外研究者在其层面力学特性、本构模型及结构仿真等方面开展了大量的研究工作。顾冲时等[1-3]针对层面影响带渐变的特性, 基于复合材料的分析理论, 利用串联和并联模型, 构建了碾压混凝土坝层面影响带渐变规律分析模型。李波等[4]研究了碾压混凝土坝并层龄期内力学参数的确定方法,并建立了基于弹性力学参数渐变的并层体分析模型。对于碾压混凝土坝耦合分析,外国学者Hariri-Ardebili等[5-6]基于拉格朗日-欧拉方法,考虑了基岩裂缝的存在,建立了大坝-基岩-水库系统的耦合模型,在输入不同类型的地震动力荷载进行结构体系的激励,分析了裂缝生成以及耦合作用下裂纹扩展的破坏机理。柴军瑞等[7-8]利用离散裂隙网络模型,分析了层面渗流与坝体应力相互影响的耦合机制,并构建了碾压混凝土坝渗流与应力两场耦合分析的数学模型[9-10]。魏博文等[11]考虑了层面相对本体薄弱的特性,建立了碾压混凝土坝层面影响带黏弹塑性流变分析模型,并给出了相应参数的确定方法,提出了基于内时损伤的碾压混凝土坝流固耦合模型[12-13]。对于两场耦合作用下碾压混凝土坝服役性态分析,上述研究大多基于黏弹性本构关系开展的研究,并考虑由施工技术引起的层内参数渐变的影响。
由此,本文从复合材料串并联原理及黏弹性本构关系的角度出发,考虑碾压层内结构压实机理的影响,分析碾压层内物理参数的渐变特性,提出了层面主要物理参数并层等效的确定方法,在对坝体流固耦合相互影响机理分析的基础上[14],建立了考虑层内参数渐变的碾压混凝土坝渗流场与应力场的耦合分析模型,并编制了相应的工程实例有限元分析程序,分析参数渐变下耦合作用对大坝结构性能的影响效应。
1 碾压层内参数并层等效分析 1.1 力学参数渐变分析目前针对碾压混凝土坝的数值模拟大都只是从宏观角度体现了碾压混凝土坝的各向异性特性,并没有真正考虑由于施工过程引起的参数渐变特性。施工过程中的激振力、振动振幅及频率等因素决定了碾压混凝土的密实度,固相要克服固相和液相的摩擦阻力,使固相被液相包裹,占据空间形成骨架从而达到理想状态的密实体。而研究表明,碾压层内激振力的传递呈现出指数衰减,可表示为[15]:
| $ P = {P_0}\exp \left( { - \beta x/2} \right) $ | (1) |
式中:P为碾压层内的混凝土压力;P0为上表面的压力;x为距上表面的深度;β为衰减系数。
由此,加速度在碾压层内也呈现指数衰减,沿层深的衰减可用下式表示:
| $ a = {a_0}\exp \left( { - \beta x/2} \right) $ | (2) |
式中:a0为上表面的加速度。
激振力的衰减致使孔隙率从碾压层上表面至底面逐渐增大,且孔隙率的变化可近似表征为线性变化。对于相同配合比的碾压混凝土而言,孔隙率越小,渗透系数越小,相应的密实度、抗压强度及弹性模量越大。
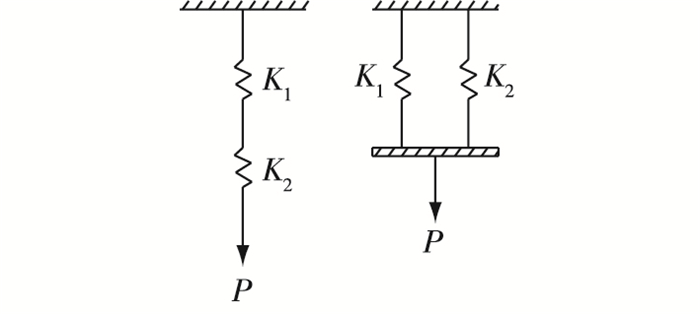
1.2 等效分析方法在对碾压层内的物理参数的渐变特性进行等效分析前,需要进行一系列的假定:①碾压层内的物理参数呈连续分布;②宏观上坝体表现为横观各向同性介质;③层面间距相等且互相平行;④各层厚度与大坝特征尺寸相比是微小量;⑤层面变形满足小变形假设。结构的等效处理首先需保证原结构总厚度与总刚度相同,通过分解刚度法来求解其等效参数。以弹簧的并串联为例进行分析,两个弹簧的刚度分别记为K1和K2,将迫使弹簧产生单位变形时所需的力定义为弹簧的刚度。弹簧的串连和并联模型见图 1。
|
图 1 弹簧的串联和并联 Figure 1 Springs in series and parallel |
串联时,在外力P的作用下,弹簧产生总的变形为w;两个弹簧承受荷载相同,产生的变形分别为w1和w2,应用刚度分解法,取K2=∞ (此时该弹簧只能传递荷载,不产生变形),K1为有限值(只有这个弹簧依旧在变形),w1为有限值时弹簧1产生的变形,总变形等于各个刚度单独作用时所产生变形的总和,这就是同类刚度K1和K2串联时所采用的分解方法[16-17]。由此得:
| $ w = {w_1} + {w_2} $ | (3) |
该式在两个刚度串联时亦具有普遍意义,由式(3)可知:
| $ {w_1} = P/{K_1},{w_2} = P/{K_2},w = P/K $ | (4) |
式中:刚度K代表两个同类刚度的综合刚度,由式(3)和(4)可得:
| $ 1/K = 1/{K_1} + 1/{K_2} $ | (5) |
式(5)就是两个弹簧串联时综合刚度的求解计算式。并联时,在外力P的作用下,两个弹簧所产生的变形一致,设总变形为w,因为荷载P由两个弹簧按刚度分担,可得:
| $ {P_1} = {K_1}w,{P_2} = {K_2}w,P = Kw $ | (6) |
| $ P = {P_1} + {P_2} $ | (7) |
由式(6)和(7)得:
| $ K' = {K_1} + {K_2} $ | (8) |
式中:刚度K′就是两个弹簧并联时的综合刚度。若将弹簧结构改成混凝土结构,可依据刚度的定义,求得混凝土结构的刚度:
| $ K' = \left( {E{l_{\rm{b}}}{l_{\rm{c}}}/{l_{\rm{a}}}} \right){\mathit{\Delta }} l $ | (9) |
式中:Δl为单位长度;E为混凝土的弹性模量;la,lb,lc分别为混凝土结构的长度、宽度和厚度。
将式(9)代入式(5)和(8),并将弹簧的个数增加至n个,经过简化可得:
| $ \left\{ \begin{array}{l} H/{E_{\rm{P}}} = {h_1}/{E_1} + {h_2}/{E_2} + \cdots + {h_n}/{E_n}\\ {E_{\rm{S}}}H = {E_1}{h_1} + {E_2}{h_2} + \cdots + {E_n}{h_n} \end{array} \right. $ | (10) |
式中:hi(i=1, 2, 3,…,n)为第i个材料的长度;Ei(i=1, 2, 3,…,n)为第i个材料的弹性模量;ES为材料串联时的综合弹性模量;EP为材料并联时的综合弹性模量;H为材料串联时的总长度。
1.3 力学参数统一变换公式关于等效弹性模量和渐变的弹性模量之间的等效变换,则以位移相同为先决条件进行。如果将碾压混凝土的碾压层分成n个小层,hi表示第i个小层的厚度;Ei表示第i个小层的弹性模量;Ev表示垂直于层面方向的综合弹性模量;Eh表示平行于层面方向的综合弹性模量;H′表示碾压层厚度。则应用式(10)时,可得:
| $ \left\{ \begin{array}{l} H'/{E_{\rm{v}}} = {h_1}/{E_1} + {h_2}/{E_2} + \cdots + {h_n}/{E_n}\\ {E_{\rm{h}}}H' = {E_1}{h_1} + {E_2}{h_2} + \cdots + {E_n}{h_n} \end{array} \right. $ | (11) |
关于等效渗透系数和渐变的渗透系数之间的等效变换,则以渗流量相同为先决条件进行。类比弹性模量,等效渗透系数与各碾压层渗透系数之间亦存在某种对应的函数关系。综上分析可知,整个坝体结构与各层水平、垂直的等效渗透系数为:
| $ {K_{\rm{h}}}H' = {k_1}{h_1} + {k_2}{h_2} + \cdots + {k_n}{h_n} $ | (12) |
| $ H'/{K_{\rm{v}}} = {h_1}/{k_1} + {h_2}/{k_2} + \cdots + {h_n}/{k_n} $ | (13) |
式中:Kh为水平向碾压层等效渗透系数;Kv为垂直向碾压层等效渗透系数。
在等效变换计算式的形式上,弹性模量和渗透系数呈现出一致性。故将等效变换公式写成如下统一变换公式:
| $ \left\{ \begin{array}{l} H'/{Y_{\rm{v}}} = {h_1}/{y_1} + {h_2}/{y_2} + \cdots + {h_3}/{y_n}\\ {Y_{\rm{h}}}H' = {y_1}{h_1} + {y_2}{h_2} + \cdots + {y_n}{h_n}\\ H' = {h_1} + {h_2} + \cdots + {h_n}\\ {y_i} = f\left( {\sum\limits_{j = 1}^i {{h_j}} } \right)\;\;\;\;\;i = 1,2, \cdots ,n \end{array} \right. $ | (14) |
式中:Yv和Yh分别为垂直和平行于层面的等效参数;H′为碾压层厚度;h为层内某一点至碾压层上表面的垂直距离;n为碾压层划分的小层数目;yi(i=1, 2, …, n)为第i个小层的参数值;hi(i=1, 2, …, n)为第i个小层的厚度。
本文虽然只讨论了弹性模量和渗透系数的等效变换,其他物理参数(如泊松比、剪切模量等)亦可以经过类似推导得到相应的等效变换式。在此,尚需指出的是模型中碾压层切向、法向的等效参数可通过试验或原位监测资料优化反演确定[18]。
2 应力场与渗流场的耦合模型 2.1 应力场与渗流场的相互影响对于服役期的碾压混凝土坝而言,位移场的改变会使坝体产生体积应变,进而引起孔隙体积的变化,从而改变坝体内部孔隙率,由此影响坝体内部的渗流场。在分析碾压混凝土坝两场耦合作用时,可依据坝体应力场与位移场的计算结果,及时将渗透系数按计算后的孔隙率予以调整,来更新结构计算渗流场[19-20]。又考虑到坝体体积应变主要由应力场所引起,对于坝体渗透系数的变化,将渗透系数设为与应力状态呈指数分布的数学函数,并将渗流主向置于应力主向,则主渗透系数为:
| $ \left[ {{k^t}} \right] = k_0^{t - 1}\left[ {\begin{array}{*{20}{c}} {\exp \left( {\lambda {{\sigma '}_x}} \right)}&{}&{}\\ {}&{\exp \left( {\lambda {{\sigma '}_y}} \right)}&{}\\ {}&{}&{\exp \left( {\lambda {{\sigma '}_z}} \right)} \end{array}} \right] $ | (15) |
式中:t为迭代步数;k0t-1是迭代步为t-1时坝体表面渗透系数;λ为影响系数,由试验确定;σ′x,σ′y,σ′z为3个渗透主轴的有效主应力。
基于有限元分析的基本原理,需先确定结构中单元的几何方程与物理方程,再建立碾压混凝土坝单元结点位移静力平衡方程,并将计算区域内所有的单元刚度矩阵进行组刚,求得结构整体总刚平衡方程;考虑大坝渗流体积力的影响,可得其结构有限元平衡方程为:
| $ \mathit{\boldsymbol{K\delta }} = \mathit{\boldsymbol{F}} + {\mathit{\boldsymbol{F}}_{\rm{S}}} $ | (16) |
| $ \mathit{\boldsymbol{K}} = \iiint {{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{DB}}{\rm{d}}V} $ | (17) |
式中:K为整体刚度矩阵;δ为位移列阵;F为外部载荷列阵;FS为渗流体积力所形成的等效载荷列阵;B为几何矩阵;D为弹性矩阵。
可将式(16)写成增量形式为:
| $ \mathit{\boldsymbol{K \boldsymbol{\varDelta} \delta = \boldsymbol{\varDelta} F}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{F}}_{\rm{S}}} $ | (18) |
式中:ΔF为坝体自重以及外荷载等引起的结点荷载增量;ΔFS为渗流场的改变引起的渗流体积力结点荷载增量;Δδ为位移增量。
2.2 耦合方程及实施步骤基于上述分析,考虑到大坝渗流场和应力场的耦合机制,方程组的有限元形式可表示为:
| $ \mathit{\boldsymbol{K \boldsymbol{\varDelta} \delta = \boldsymbol{\varDelta} F}} + \mathit{\boldsymbol{ \boldsymbol{\varDelta} }}{\mathit{\boldsymbol{F}}_{\rm{S}}} $ | (19) |
| $ \mathit{\boldsymbol{kh}} + \mathit{\boldsymbol{H}}\frac{{\partial \mathit{\boldsymbol{h}}}}{{\partial t}} = \mathit{\boldsymbol{p}} $ | (20) |
| $ k = k'{\left\{ {\frac{{n\left( {1 - {n_0}} \right)}}{{{n_0}\left( {1 - n} \right)}}} \right\}^3}或\;k = k\left( {{\sigma _{ij}}} \right) $ | (21) |
式中:h为总压力水头列向量;∂h/∂t为总水头对时间导数的列向量;p为等效结点流量向量;k为总渗流矩阵;H为总水头对时间导数变化率矩阵;K为整体刚度矩阵;k, k′分别为孔隙比取n和n0时碾压层的渗透系数。
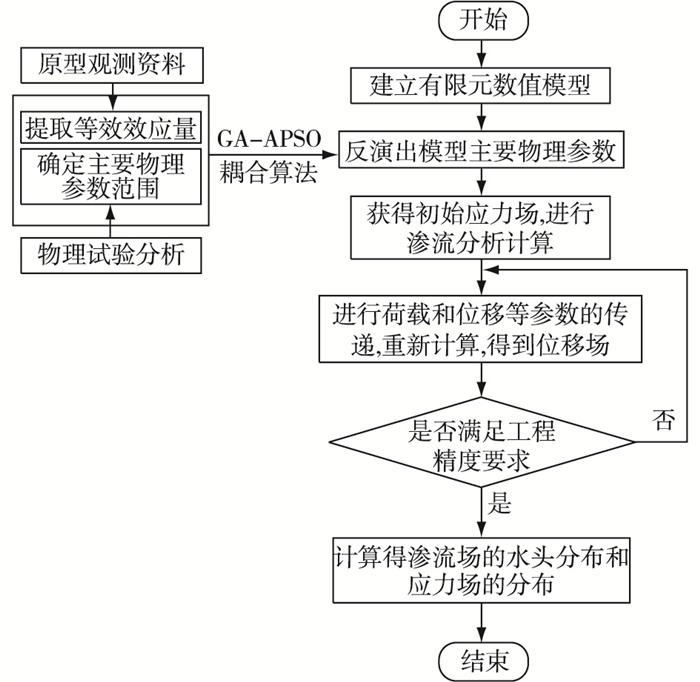
式(18)~(21)已给出了碾压混凝土坝渗流与应力两场耦合的数学模型,该模型的求解问题为一非线性问题,难以获得精确的解析值,需通过数学计算方法进行迭代获取其满足工程精度要求的数值解,其具体迭代流程如图 2。
|
图 2 迭代流程 Figure 2 Iterative flow chart |
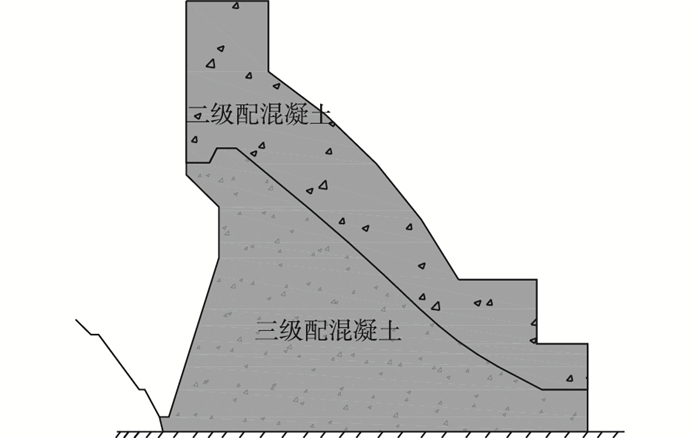
以某碾压混凝土重力坝的8#坝段为例,该坝段为全断面碾压混凝土坝,最大坝高160 m,坝顶宽26 m。有限元计算模型见图 3,坝体上游的作用水头为154 m,大坝基岩的弹性模量取21 GPa。由于对力学参数的未知性以及结构的劣化损伤的影响,流固耦合分析计算时应采用综合弹性模量,参照6#坝段的反演结果进行等效分析,最终取坝体综合弹性模量为25.8 GPa。坝底建基面设有一层常态混凝土垫层,从上游往下依次是二级配碾压混凝土和三级配碾压混凝土,坝体、坝基均布设了防渗排水系统,具体材料分区见图 4。为实现防渗孔幕的数值模拟,本文采用夹层单元来模拟帷幕防渗效果,运用帷幕厚度来确定单元厚度[21-22]。对于碾压混凝土坝层面影响带厚度的确定,可利用单位宽度的本体和层面影响带的渗水量等于获取总渗水量来[23],鉴于施工时各碾压层之间的厚度为30 cm,参照文献[23],在模拟分析中将其层面影响带厚度平均取为1 cm。

|
图 3 有限元模型 Figure 3 Finite element model |
|
图 4 8#坝段典型剖面 Figure 4 Typical profile of 8# dam |
计算中渗透系数取值为:常态混凝土为1.0×10-7 cm/s;二级配RCC本体渗透系数为1.0×10-7 cm/s;三级配RCC为1.0×10-6 cm/s;防渗帷幕为1.0×10-7 cm/s;坝基为1.0×10-5 cm/s;结合良好和结合不良情况下层面水力影响带的渗透系数分别取为比本体渗透系数大2个和4个数量级。
3.2 计算结果分析依据上述耦合模型及相应工程的有限元程序对该坝段进行了计算分析,获得了耦合作用下的渗流场和应力场,并与未考虑耦合作用的结果进行了比较。图 5为渗流场等势线比较图,应力场σz (垂直于层面方向)和σx (平行于层面方向)比较分别见图 6和图 7。

|
图 5 渗流场等势线比较 Figure 5 Equipotential lines of seepage field |

|
图 6 σz等值线(单位:MPa) Figure 6 σz contour maps (unit: MPa) |

|
图 7 σx等值线(单位:MPa) Figure 7 σx contour maps (unit: MPa) |
由图 5~7可见,未考虑耦合作用与考虑耦合作用的渗流场、应力场分布规律基本一致。但较未考虑耦合作用而言,耦合作用后的基岩渗流等势线略微右移,坝体内部的渗流等势线略微下移。这是由于水库蓄水使得坝体受压,导致坝体及基岩渗透系数减小,致使库水不易排出,s从而使得坝基面下游面扬压力增大。此外,耦合作用造成坝体上游部位的σz压应力减小,坝体下游坝踵部位的σz压应力增大(使σz最大压应力增大约11.3%),甚至坝踵部分区域都出现拉应力,坝踵、坝趾处呈现出明显的应力集中现象,主要由考虑耦合作用时垂直于层面的渗透压力引起,靠近坝体上游面的排水孔有效地降低了排水孔后坝体的扬压力,整体而言坝体上游侧的扬压力大于下游侧所导致的。由图 7可知,坝体及坝基整体在水平向压应力较未考虑耦合作用时变大,这主要是因为上下游水位差在耦合作用下,坝体各个层面和坝基的渗流作用引起的切向拖曳力所致。不考虑渗流只考虑应力场单独作用时,坝体及坝基大部分区域为压应力区;而渗流场作用时,除了渗透水流产生的拖拽力之外,还将产生浮力,因此渗流场和应力场在此区域呈现为负相关作用;而单独应力场作用时的拉应力区或者水力梯度较大的区域内两场呈现正相关。
4 结语本文从筑坝施工碾压机理角度,分析了碾压层本体与层面渐变力学特性,且推导了层内物理参数的等效统一变换式,并依据文中所述的耦合分析模型,结合某工程实例编制了相应的有限元分析程序,分析了渗流场与应力场耦合作用下某在役碾压混凝土坝的服役性态。结果表明:考虑耦合作用致使坝体的应力增大,不利于大坝等水工建筑物的稳定;若不考虑耦合作用的影响效应,则可能会夸大排水设施的作用,亦与实际不符。从理论上说,运用耦合作用后的应力场来推求大坝的稳定性更接近实际情况;且耦合作用激励下不利因素的影响效应亦可为一线人员的施工提供技术支持。
| [1] |
顾冲时, 宋敬衖, 方海挺. 碾压混凝土坝层面影响带渐变规律分析模型[J]. 应用数学和力学, 2006, 27(11): 1335-1340. ( GU Chongshi, SONG Jingxiang, FANG Haiting. Analysis model on gradual change principle of effect zones of layer face for RCCD[J]. Applied Mathematics and Mechanics, 2006, 27(11): 1335-1340. DOI:10.3321/j.issn:1000-0887.2006.11.010 (in Chinese)) |
| [2] |
顾冲时, 李波, 虞鸿, 等. 碾压混凝土坝力学参数的反分析[J]. 中国科学:技术科学, 2010, 40(6): 651-656. ( GU Chongshi, LI Bo, YU Hong, et al. Back analysis of mechanical parameters of roller compacted concrete dam[J]. Scientia Sinica (Technologica), 2010, 40(6): 651-656. (in Chinese)) |
| [3] |
顾冲时, 吴中如, 吴相豪. 碾压混凝土坝安全监控理论和方法[J]. 水利学报, 2002(9): 112-116. ( GU Chongshi, WU Zhongru, WU Xianghao. A review on development of theory and method for safety monitoring of roller compacted concrete dam[J]. Journal of Hydraulic Engineering, 2002(9): 112-116. (in Chinese)) |
| [4] |
李波, 顾冲时, 武金坤. 碾压混凝土坝弹性力学参数渐变规律分析[J]. 水利学报, 2013, 44(12): 1488-1497. ( LI Bo, GU Chongshi, WU Jinkun. Gradual change law of elastic mechanical parameters of roller compacted concrete dam[J]. Journal of Hydraulic Engineering, 2013, 44(12): 1488-1497. (in Chinese)) |
| [5] |
HARIRI-ARDEBILI M A, SEYED-KOLBADI S M, KIANOUSH M R. FEM-based parametric analysis of a typical gravity dam considering input excitation mechanism[J]. Soil Dynamics and Earthquake Engineering, 2016, 84: 22-43. DOI:10.1016/j.soildyn.2016.01.013 |
| [6] |
KALATEH F, KOOSHEH A. Comparing of loose and strong finite element partitioned coupling methods of acoustic fluid-structure interaction: Concrete dam-reservoir system[J]. KSCE Journal of Civil Engineering, 2017, 21(3): 807-817. DOI:10.1007/s12205-016-0276-0 |
| [7] |
柴军瑞, 仵彦卿. 岩体渗流场与应力场耦合分析的多重裂隙网络模型[J]. 岩石力学与工程学报, 2000, 19(6): 712-717. ( CHAI Junrui, WU Yanqing. Research on multiple-level fracture network model for coupled seepage and stress fields in rock mass[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(6): 712-717. (in Chinese)) |
| [8] |
柴军瑞, 仵彦卿. 碾压混凝土坝渗流场与应力场耦合分析的数学模型[J]. 水利学报, 2000(9): 33-37. ( CHAI Junrui, WU Yanqing. Mathematical model for couple analysis of seepage and stress fields in RCCD[J]. Journal of Hydraulic Engineering, 2000(9): 33-37. (in Chinese)) |
| [9] |
顾冲时, 苏怀智, 周红. 碾压混凝土坝渗流场与应力场耦合模型研究[J]. 应用数学和力学, 2005, 26(3): 325-332. ( GU Chongshi, SU Huaizhi, ZHOU Hong. Study on coupling model of seepage-field and stress-field for RCCD[J]. Applied Mathematics and Mechanics, 2005, 26(3): 325-332. (in Chinese)) |
| [10] |
TANG C A, THAM L G, LEE P K K, et al. Coupled analysis of flow, stress and damage (FSD) in rock failure[J]. International Journal of Rock Mechanics and Mining Sciences, 2002, 39(4): 477-489. DOI:10.1016/S1365-1609(02)00023-0 |
| [11] |
魏博文, 徐镇凯, 徐宝松. 碾压混凝土坝层面影响带黏弹塑性流变模型[J]. 水利学报, 2012, 43(9): 1097-1102. ( WEI Bowen, XU Zhenkai, XU Baosong. Viscoelasto-plastic rheological model of effect zone for RCCD[J]. Journal of Hydraulic Engineering, 2012, 43(9): 1097-1102. (in Chinese)) |
| [12] |
魏博文, 乐豪峰, 胡凯, 等. 基于内时损伤的混凝土拱坝结构分析方法研究[J]. 水电能源科学, 2012, 30(3): 77-80. ( WEI Bowen, LE Haofeng, HU Kai, et al. Structure analysis method of concrete arch dam based on endochronic damage[J]. Water Resources and Power, 2012, 30(3): 77-80. (in Chinese)) |
| [13] |
KATAOKA S, MINAMI S, KAWAI H, et al. A parallel iterative partitioned coupling analysis system for large-scale acoustic fluid-structure interactions[J]. Computational Mechanics, 2014, 53(6): 1299-1310. DOI:10.1007/s00466-013-0973-1 |
| [14] |
GU Chongshi, WEI Bowen, XU Zhenkai, et al. Fluid-solid coupling model based on endochronic damage for roller compacted concrete dam[J]. Journal of Central South University, 2013, 20(11): 3247-3255. DOI:10.1007/s11771-013-1848-5 |
| [15] |
陈龙, 吴中如, 顾永明. 碾压混凝土坝层内力学参数渐变分析模型[J]. 水利学报, 2006, 37(3): 325-330. ( CHEN Long, WU Zhongru, GU Yongming. Analytic model for gradual variation of concrete intra-layer mechanical parameters in RCCD[J]. Journal of Hydraulic Engineering, 2006, 37(3): 325-330. (in Chinese)) |
| [16] |
朱伯芳. 多层混凝土结构仿真应力分析的并层算法[J]. 水力发电学报, 1994(3): 21-30. ( ZHU Bofang. Mixed-layer method for alalysis of stresses by simulating the construction process of multilayered high concrete structures[J]. Journal of Hydroelectric Engineering, 1994(3): 21-30. (in Chinese)) |
| [17] |
ZHU N, HU P, XU L. A simplified dynamic model of double layers shape-stabilized phase change materials wallboards[J]. Energy and Buildings, 2013, 67(4): 508-516. |
| [18] |
魏博文, 徐镇凯, 李火坤, 等. 基于GA-APSO混合罚模型的混凝土坝力学参数优化反演[J]. 中南大学学报(自然科学版), 2015, 46(11): 4211-4217. ( WEI Bowen, XU Zhenkai, LI Huokun, et al. Optimization inversion for mechanical parameters of concrete dam based on GA-APSO mixed penalty model[J]. Journal of Central South University(Science and Technology), 2015, 46(11): 4211-4217. DOI:10.11817/j.issn.1672-7207.2015.11.031 (in Chinese)) |
| [19] |
张奇华, 李玉婕, 袁东, 等. 地下水封洞库水幕孔注水试验及岩体等效渗透参数分析[J]. 岩土力学, 2015, 36(9): 2648-2658. ( ZHANG Qihua, LI Yujie, YUAN Dong, et al. Water injection test about water curtain borehole for underground water-sealed cavern and analysis of rock equivalent permeability parameter[J]. Rock and Soil Mechanics, 2015, 36(9): 2648-2658. (in Chinese)) |
| [20] |
刘武, 陈益峰, 胡冉, 等. 基于非稳定渗流过程的岩体渗透特性反演分析[J]. 岩石力学与工程学报, 2015, 34(2): 362-373. ( LIU Wu, CHEN Yifeng, HU Ran, et al. Back analysis of rock permeability with consideration of transient flow process[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(2): 362-373. (in Chinese)) |
| [21] |
朱岳明, 龚道勇, 章洪, 等. 碾压混凝土坝渗流场分析的缝面渗流平面单元模拟法[J]. 水利学报, 2003(3): 63-68. ( ZHU Yueming, GONG Daoyong, ZHANG Hong, et al. Plan element simulation of fracture seepage for analyzing seepage in RCC dams[J]. Journal of Hydraulic Engineering, 2003(3): 63-68. (in Chinese)) |
| [22] |
彭鹏, 单治钢, 宋汉周, 等. 反映坝基帷幕体防渗时效的多场耦合数值模拟[J]. 岩土工程学报, 2011, 33(12): 1847-1853. ( PENG Peng, SHAN Zhigang, SONG Hanzhou, et al. Coupling model for assessing anti-seepage behaviors of curtain of dam foundation[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1847-1853. (in Chinese)) |
| [23] |
彭友文, 顾冲时, 吴中如. 碾压混凝土坝层面影响带厚度分析[J]. 长江科学院院报, 2005, 22(4): 59-61. ( PENG Youwen, GU Chongshi, WU Zhongru. Analysis on effect-zone thickness of RCCD[J]. Journal of Yangtze River Scientific Research Institute, 2005, 22(4): 59-61. (in Chinese)) |
 2017
2017 
