2. 浙江华东工程数字技术有限公司,浙江 杭州 311100
洪泽湖是淮河流域防洪排涝建设中的重要组成部分,作为淮河中下游结合部的平原湖泊型水库[1],承泄了淮河上中游15.8万km2面积产生的洪水[2]。然而,在现有的工程规模条件下,洪泽湖的防洪标准低,周边蓄滞洪区的启用标准不到50年一遇[3]。遭遇中等洪水及大洪水时,在充分利用周边滞洪区的情况下,洪泽湖洪水位仍偏高,出湖口泄洪能力明显不足,增加了洪泽湖大堤的安全隐患,加大了淮河中下游地区的防洪排涝压力[4]。为解决这一问题,巩固和加强淮河入海能力,提高洪泽湖的调蓄能力,扩建淮河入海水道工程应运而生。淮河入海水道一期工程设计流量2 270 m3/s[5],2003年通过通水验收,同年6月淮河流域受多次强降雨影响,发生了仅次于1954年的大洪水,为减轻洪泽湖防洪压力,入海水道提前使用,在缓解洪泽湖汛情中发挥了重要作用[5]。此后,淮河流域又多次遭遇大洪水,洪泽湖水位居高不下,洪水出路规模偏小的问题日益突出,为提高洪泽湖及下游防洪保护区的防洪标准,规划建设入海水道二期工程。2015年11月,入海水道二期工程可研报告通过审批。
数值模拟是洪水风险分析的重要手段。利用风险分析数值模型可以预先模拟历史洪水、实时洪水和未来可能的洪水,根据模型计算结果可以预先评估防洪调度措施的作用和效果[6],在评估的基础上修订和完善不合理的调度方案,降低由于调度指令不合理带来的风险,使防洪调度决策者能更合理地做出决策。本文在充分掌握洪泽湖地区工程调度情况以及相关水文边界资料的基础上,构建一、二维耦合的动态洪水演进数值模型,利用已构建的模型模拟不同设计洪水下蓄滞洪区内洪水演进情况,根据模拟结果,分别从定性、定量的角度评价淮河入海水道二期工程对洪泽湖地区防洪风险的影响。
1 一、二维耦合数值模型 1.1 模型控制方程及求解河道一维模型的控制方程为圣维南方程组[7](De Saint-Venant System of Equations),如式(1)和(2)所示。通过有限差分方法对方程进行离散,有限差分格式为6点中心Abbott-Ionescu格式。计算网格由流量点和水位点组成,其中流量点和水位点在同一时间步骤下分别进行计算,水位点位于横断面所在位置,流量点位于两个相邻的水位点之间。
| $ {\rm{连续方程:}}\frac{{\partial \mathit{Q}}}{{\partial \mathit{x}}}{\rm{ + }}\frac{{\partial \mathit{A}}}{{\partial \mathit{t}}}{\rm{ = }}{\mathit{q}_{\rm{t}}} $ | (1) |
| $ {\rm{运动方程:}}\frac{{\partial \mathit{Q}}}{{\partial \mathit{t}}} + \frac{\partial }{{\partial \mathit{x}}}\left( {\mathit{\alpha }\frac{{{\mathit{Q}^{\rm{2}}}}}{\mathit{A}}} \right) + \mathit{gA}\frac{{\partial \mathit{Z}}}{{\partial \mathit{x}}} + \mathit{gA}\frac{{\left| \mathit{Q} \right|\mathit{Q}}}{{{\mathit{K}^{\rm{2}}}}} = 0 $ | (2) |
式中:Q为断面过水流量;A为过水面积;x为沿程距离;t为时间;qt为区间来水;Z为断面水位;α为动量修正系数;K为流量模数。
洪泛区二维模型的控制方程[8]由连续方程和水流运动方程组成。通过有限体积法对方程进行离散,变量u, v位于单元中心,跨边界通量垂直于单元边。有限体积法中法向通量通过在沿外法向建立单元水力模型并求解一维黎曼问题得到。采用显式时间积分。
| $ {\rm{连续方程:}}\frac{{\partial \mathit{\xi }}}{{\partial \mathit{t}}} + \frac{{\partial \left( {\mathit{hu}} \right)}}{{\partial \mathit{x}}} + \frac{{\partial \left( {\mathit{hv}} \right)}}{{\partial \mathit{y}}} = \mathit{q} $ | (3) |
| $ \begin{array}{l} {\rm{运动方程:}}\\ \frac{{\partial \left( {\mathit{hu}} \right)}}{{\partial \mathit{t}}}{\rm{ + }}\frac{\partial }{{\partial \mathit{x}}}\left( {\mathit{huu}} \right){\rm{ + }}\frac{\partial }{{\partial \mathit{y}}}\left( {\mathit{hvv}} \right){\rm{ = }}\frac{\partial }{{\partial \mathit{x}}}{\rm{(}}\mathit{h}{\mathit{E}_\mathit{y}}\frac{{\partial \mathit{u}}}{{\partial \mathit{x}}}{\rm{) + }}\\ \frac{\partial }{{\partial \mathit{y}}}{\rm{(}}\mathit{h}{\mathit{E}_\mathit{x}}\frac{{\partial \mathit{u}}}{{\partial \mathit{y}}}{\rm{) + }}\mathit{fhv}{\rm{ - }}\mathit{gH}\frac{{\partial \mathit{\xi }}}{{\partial \mathit{x}}}{\rm{ - }}\frac{1}{\mathit{\rho }}{\rm{(}}{\mathit{\tau }_{{\rm{b}}\mathit{x}}}{\rm{ - }}{\mathit{\tau }_{{\rm{s}}\mathit{x}}}{\rm{) + }}\mathit{q}{\mathit{u}^{\rm{*}}} \end{array} $ | (4) |
| $ \begin{array}{l} \frac{{\partial \left( {\mathit{hv}} \right)}}{{\partial \mathit{t}}}{\rm{ + }}\frac{\partial }{{\partial \mathit{x}}}\left( {\mathit{huv}} \right){\rm{ + }}\frac{\partial }{{\partial \mathit{y}}}\left( {\mathit{hvu}} \right){\rm{ = }}\frac{\partial }{{\partial \mathit{y}}}{\rm{(}}\mathit{h}{\mathit{E}_\mathit{y}}\frac{{\partial \mathit{v}}}{{\partial \mathit{x}}}{\rm{) + }}\\ \frac{\partial }{{\partial \mathit{y}}}{\rm{(}}\mathit{h}{\mathit{E}_\mathit{x}}\frac{{\partial \mathit{v}}}{{\partial \mathit{y}}}{\rm{) + }}\mathit{fhu}{\rm{ - }}\mathit{gH}\frac{{\partial \mathit{\xi }}}{{\partial y}}{\rm{ - }}\frac{1}{\mathit{\rho }}{\rm{(}}{\mathit{\tau }_{{\rm{b}}\mathit{y}}}{\rm{ - }}{\mathit{\tau }_{{\rm{s}}\mathit{y}}}{\rm{) + }}\mathit{q}{\mathit{v}^{\rm{*}}} \end{array} $ | (5) |
式中:h, ξ为水深和水位;u, v分别为x, y方向的垂向平均流速;Ex, Ey分别为x和y方向的水流紊动黏性系数;τbx,τby为x方向和y方向的底部摩阻;τsx,τsy分别为风对自由表面x和y方向的剪切力;f=2ωsinϕ为科氏力,ϕ为计算水域的地理纬度。Q为源或汇单位面积的流量,源取正,汇取负;u*,v*分别为源或汇输入输出时在x和y方向的流速。
为保证模型计算的连续性,设置了干湿边界,处理技术采用Sleigh等[9]的研究成果,当网格单元上的水深变浅但尚未处于露滩状态时,相应水动力计算采用特殊处理,即该网格单元上的动量通量值为0,只考虑质量通量;当网格上的水深变浅至露滩状态时,计算中将忽略该网格单元直至其被重新淹没为止。
1.2 建模范围本次计算范围为16.83 m(85高程,下同)等高线以及泗洪、泗阳、盱眙部分高地所构成的区域,包括洪泽湖湖面及相关河道、滞洪区、鲍集圩行洪区、高地,总面积为4 395.5 km2。如图 1所示。
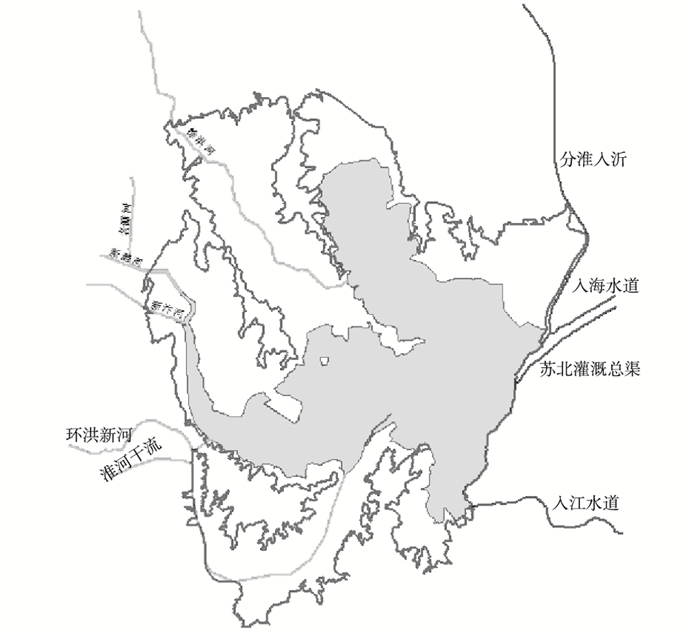
|
图 1 计算范围内骨干河道和泄洪出口 Figure 1 Main rivers and flood outlets in the region |
洪泽湖周边滞洪区内河网纵横交错、水系复杂,本次建模提取了对洪水分析比较重要的一些河流来构造河网模型,包括淮河、怀洪新河、徐洪河、新汴河、新濉河、老濉河、西民便河、安东河、利民河、濉河等主要通湖河道,入江水道、入海水道、分淮入沂和灌溉总渠4个出湖通道,以及322条圩内河道等[10]。
1.4 边界条件一维河网模型的上、下游边界的控制条件一般采用水位过程控制、流量过程控制、流量水位关系控制等形式。本次研究区内采用各主要通湖河道的设计入湖过程作为模型输入的上边界,以三河闸、二河闸和高良涧闸的水位流量关系作为下边界条件。
1.5 网格剖分采用非结构不规则网格对研究区进行网格划分,网格设计成大小不等的三角形,使网格的大小随地形地势和阻水建筑物的分布灵活确定,而且尽可能地将影响水流的阻水建筑物作为网格边界[11],充分反映计算域的特征。但是,必要的时候对区域内的一些典型的线性阻水建筑物(如堤防、公路等)合理概化,并对网格适当加密,在二维地形中充分反映其特征。研究区最大网格面积不超过0.1 km2,洪泽湖湖面网格适当放大,最大网格面积不超过1 km2,共剖分网格85 894个。
1.6 耦合模型在处理通湖河道与洪泽湖湖区、进洪口门与洪泛区的连接时,一维模型为二维模型提供流量值Q并作为二维模型的边界条件,将Q值分布到二维计算单元的各节点上;在连接处二维计算网格的水位值并不相等,因此取各个计算网格的平均水位值Z返回给一维模型,以进行下一时段的计算。在处理实测河道与洪泛区的连接时,耦合模型将二维模型的网格单元从侧面连接到一维模型的部分河段甚至是整个河段,利用建筑物的流量公式来计算通过侧向连接的水流[12]。
1.7 模型的率定和验证计算建国以来,淮河流域发生过1954,1991,2003,2006和2007年大水,但由于现状工况与1954年工况相比,有很大改变,故本次选取1991和2006年作率定年份,2003和2007年作验证年份。
1.7.1 模型的率定糙率是表征河道底部、岸坡和洪泛区地表影响水流阻力的综合系数,是水力计算的重要参数,也是水动力数学模型中最重要的参数。根据下垫面条件不同对糙率进行分区,主要包括一维河道糙率和二维洪泛区糙率等。采用1991和2006两个实况年的降雨资料和洪泽湖的出湖水位资料对模型的参数进行率定计算,得:一维河道糙率为0.018~0.025,洪泽湖湖面糙率为0.025~0.033,其中疏浚过的、较规则的河槽糙率取0.018,其余河槽糙率取0.025,洪泽湖湖面总体糙率取0.025,由于如栗河洼等部分为芦苇荡,糙率较大,这些区域糙率取0.033。
1.7.2 模型的验证计算根据之前率定确定的模型参数,采用2003年、2007年的实测降雨和洪泽湖的出湖水位及蒋坝、临淮头等4个水文站的水资料对模型进行验证,模型计算范围内水文站的分布见图 2。
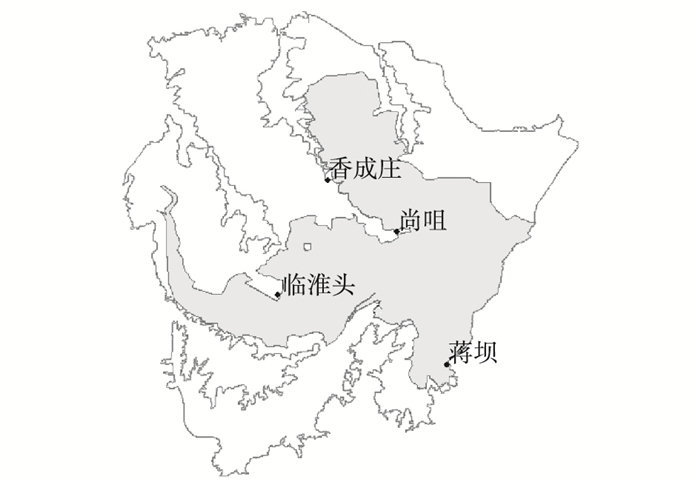
|
图 2 率定验证所用水文站地理位置分布 Figure 2 Hydrological stations used for calibration and verification |
将实测次降雨过程、洪泽湖出湖流量过程输入模型进行模拟计算,比较模拟得到的4个水文站的水位过程值与实测值,结果见表 1。图 3仅列出临淮头站、香城庄站2003年、2007年两次模拟计算的水位过程与实测过程的对比。由图表结果可知,数值模拟水位过程比较符合实际情况,计算值与实测值符合较好,说明模型能反应洪水演进的物理机制。
| 表 1 水位过程参数统计 Table 1 Parameter statistics of water level |

|
图 3 2003和2007年水位实测值与计算值对比 Figure 3 Comparison of water level between measured and calculated values in 2003 and 2007 |
为研究海道二期工程启用后对洪泽湖洪水位以及周边滞洪区的具体影响,特设置以下5个方案供模拟计算,见表 2。模型上边界为洪泽湖50/100/300年一遇设计入湖洪水过程,下边界为三河闸、二河闸、高良涧闸出湖口水位-流量关系,蒋坝初始水位均为13.33 m,当洪泽湖水位达到滞洪水位时,即蒋坝水位达到14.33 m时,314个圩区同时滞洪。入海水道二期工程建成前后二河闸水位流量关系见表 3。
| 表 2 计算方案设置情况 Table 2 Scheme settings |
| 表 3 入海水道水位-流量关系 Table 3 Q-h relationship of sea-entering channel |
(1) 方案1、方案2与方案3对比。方案1,2和3的模拟结果见图 4。对比方案2和方案3,洪泽湖100年一遇条件下,蒋坝最高水位由15.16 m降至14.50 m,滞洪区开始滞洪时间推迟了6 d,缩短了部分圩区的淹没历时。对比方案1和方案3,规划工况下100年一遇的蒋坝最高水位比现状工况下50年一遇的蒋坝最高水位低0.1 m,滞洪区开始滞洪时间推迟1 d,可见,随着海道二期工程的启用,洪泽湖周边滞洪区的启用标准也由不到50年一遇提升至近百年一遇。
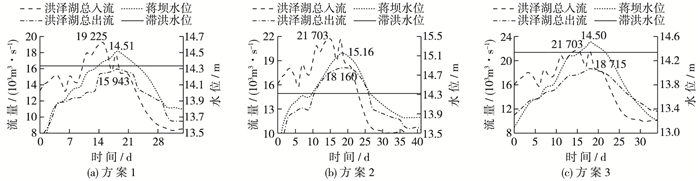
|
图 4 洪泽湖总入流、总出流及蒋坝水位过程 Figure 4 Process of inflow, outflow and water level of Hongze Lake |
(2) 方案4与方案5对比。方案4和5的模拟结果见图 5。相较方案1和方案2,随着入湖洪水量级的提高,蒋坝水位明显升高,滞洪区滞洪时间提前,最大滞洪量增大。方案5规划工况300年一遇条件下,蒋坝最高水位15.24 m,比方案4现状工况300年一遇降低了0.67 m,与方案2现状工况100年一遇中蒋坝最高水位仅相差0.08 m,可见随着海道二期的启用,洪泽湖的防洪能力有了显著的提高。
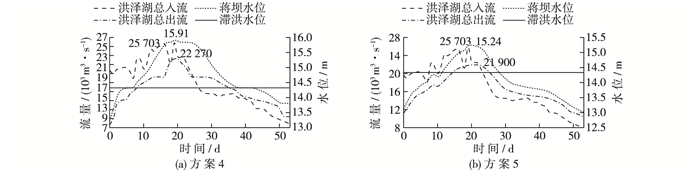
|
图 5 洪泽湖总入流、总出流及蒋坝水位过程 Figure 5 Process of inflow, outflow and water level of Hongze Lake |
不同淹没水深对应的淹没面积、不同淹没历时对应的淹没面积见表 4。根据对比,无论是现状工况之间,还是规划工况之间,随着洪水量级的提高,淹没面积均相应增大。规划工况实施入海水道二期,洪泽湖泄洪能力加大,洪泽湖水位相应降低,因此方案3、方案5分别比同等洪水量级下的方案2、方案4的淹没面积明显减小,并且减小的淹没面积大多分布在2.0 m以上。
| 表 4 不同淹没水深对应的淹没面积 Table 4 Submerged area under different submerged depths |
运用中国水利水电科学研究院开发的“洪灾损失评估模型”对研究区进行洪水影响分析。该模型基于GIS软件的叠加分析功能,将淹没图层分别与行政区图层、居民地图层相叠加,运用人民生活表中乡村人口和城镇人口数,即可得到对应不同洪水方案下的淹没人口数据。再根据项目区的水深-损失率关系,统计得到不同洪水方案的洪灾损失GDP。各方案下统计数据见表 5,对比方案2和方案3,方案4和方案5,海道二期工程的投入使用,在同等级洪水量级下,可以有效减少受灾人口14~15万人,降低受影响GDP达35万元左右。
| 表 5 洪水影响统计 Table 5 Statistics of flood influence |
针对洪泽湖周边滞洪区滞洪面积大,河网纵横交错、水系复杂的特点,建立了一维河网与二维洪泛区耦合的水动力模型。采用4年历史洪水资料对模型进行率定验证,实测值和计算值的拟合精度较高,反映了模型建立的合理性和准确性。
为解决洪泽湖周边滞洪区启用标准低,洪泽湖出湖口泄流能力不足的问题,启动淮河入海水道二期工程,增大洪泽湖出湖口之一二河闸的泄洪能力,并用数值模型加以预测。模拟结果表明,入海水道二期的启用可有效将洪泽湖周边滞洪区的启用标准从50年一遇提高至100年一遇,湖区的防洪标准也得到大幅提升,缓解了入江水道、灌溉总渠、分淮入沂的防洪压力。
| [1] |
吴晓兵. 洪泽湖60年的变迁[J]. 中国水利, 2009(14): 21-23. ( WU Xiaobing. Change of Hongze lake over 60 years[J]. China Water Resources, 2009(14): 21-23. DOI:10.3969/j.issn.1000-1123.2009.14.009 (in Chinese)) |
| [2] |
张琳, 李松柏, 张苗, 等. 南水北调东线工程对淮安城市用水的影响[J]. 人民长江, 2008(11): 28-30. ( ZHANG Lin, LI Songbai, ZHANG Miao, et al. Influence of east route of South-to-North Water Transfer Project on urban water consumption in Huai'an City[J]. Yangtze River, 2008(11): 28-30. DOI:10.3969/j.issn.1001-4179.2008.11.009 (in Chinese)) |
| [3] |
方高干, 王道虎, 罗静. 降低淮河流域中下游地区特大洪水威胁的思考[J]. 中国防汛抗旱, 2013(2): 66-68. ( FANG Gaogan, WANG Daohu, LUO Jing. Thought on reducing the threat of extreme flood in middle and lower reaches of Huaihe River basin[J]. China Flood & Drought Management, 2013(2): 66-68. (in Chinese)) |
| [4] |
赵立华. 淮河入海水道海口闸研究与实践[D]. 南京: 河海大学, 2006. (ZHAO Lihua. Research and practice on Haikou gate of sea-entering channel[D]. Nanjing: Hohai University, 2006.(in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10294-2006044109.htm
|
| [5] |
黄利亚, 闻余华. 淮河入海水道在2003年大洪水中的作用分析[J]. 水利水电技术, 2006(2): 96-97. ( HUANG Liya, WEN Yuhua. Analysis on the founction of Huaihe River sea-entering channel during flood in 2003[J]. Water Resources and Hydropower Engineering, 2006(2): 96-97. (in Chinese)) |
| [6] |
刘海娇. 基于一维、二维水力学耦合计算模型的洪水风险分析研究[D]. 天津: 天津大学, 2012. (LIU Haijiao. Research on flood risk analysis based on one-dimensional and two-dimensional hydraulic coupling calculation model[D]. Tianjin: Tianjin University, 2012.(in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10056-1013040528.htm
|
| [7] |
苑希民, 薛文宇, 冯国娜, 等. 溃堤洪水分析的一、二维水动力耦合模型及应用[J]. 水利水电科技进展, 2016, 36(4): 53-58. ( YUAN Ximin, XUE Wenyu, FENG Guona, et al. A coupled one and two-dimensional hydrodynamic model for analysis of levee-breach flood and its application[J]. Advances in Science and Technology of Water Resources, 2016, 36(4): 53-58. DOI:10.3880/j.issn.1006-7647.2016.04.010 (in Chinese)) |
| [8] |
虞邦义, 倪晋, 杨刑菊, 等. 淮河干流浮山至洪泽湖出口段水动力数学模型研究[J]. 水利水电技术, 2011, 42(8): 38-42. ( YU Bangyi, NI Jin, YANG Xingju, et al. Research on hydrodynamic numerical model for main stream of Huaihe river from Fushan to outlet of Hongze lake[J]. Water Resources and Hydropower Engineering, 2011, 42(8): 38-42. (in Chinese)) |
| [9] |
SINGH V P, SCARLATOS C A. Breach erosion of earth fill dams and flood routing BEED model[R]. North Carolina: Amy Research Office, Battelle, Research Triangle Park, 1989.
|
| [10] |
杨士健. 洪泽湖湿地自然保护区规划建设探讨[J]. 环境科学与技术, 2004, 27(4): 38-39, 90. ( YANG Shijian. Discussion on planning of wetland conservative zone in Hongze lake[J]. Environmental Science and Technology, 2004, 27(4): 38-39, 90. (in Chinese)) |
| [11] |
郑敬伟, 王艳艳, 孙德威. 杜家台蓄滞洪区洪水风险图编制[J]. 中国防汛抗旱, 2010(5): 64-67. ( ZHENG Jingwei, WANG Yanyan, SUN Dewei. Flood risk mapping in detention basin in Dujiatai[J]. China Flood and Drought Management, 2010(5): 64-67. (in Chinese)) |
| [12] |
杨志, 冯民权. 溃口近区二维数值模拟与溃坝洪水演进耦合[J]. 水利水运工程学报, 2015(1): 9-19. ( YANG Zhi, FENG Mingquan. 2D numerical simulation of breach area and coupling simulation of dam-breach flood[J]. Hydro-Science and Engineering, 2015(1): 9-19. (in Chinese)) |
2. Zhejiang Huadong Engineering Digital Technology Corporation Limited, Hangzhou 311100, China
 2017
2017 