2. 重庆交通大学 水利水运工程教育部重点实验室,重庆 400074;
3. 重庆市信息通信咨询设计院有限公司,重庆 400041
丁坝是常见的航道整治建筑物,具有改善航道、维护河相和保护水生态等功用。航道整治中,一般可根据滩险碍航特性选用某级水位将丁坝设计成单一断面型式(以下简称“单式断面丁坝”),但在某些河段,由于汛期淤积严重,退水期冲刷不及,经常出浅碍航,如果只采用一级整治水位将难以达到设计的航道尺度标准。为使洪水期少淤,退水期早冲,必须采用中水整治(或洪水整治)与枯水整治相结合的方法,同时为减小对洪水壅高的影响,较高一级整治水位所对应的整治线宽度必须适当增加[1],从而形成阶梯形丁坝(或称“复式断面丁坝”)。目前,阶梯形丁坝已广泛应用于诸多河段的航道整治工程中,如三峡水库变动回水区胡家滩滩段、珠江三角洲的东平水道、顺德菊花湾险段以及西江中游界首至肇庆河段等[2]。
丁坝的修建将改变河床局部形貌并形成独特的水流流态,回流区是丁坝水流分区的重要组成部分,其水力特性直接影响船舶通航、坝田淤积及堤岸稳定,一直备受学术界和工程界关注。比如回流尺度方面,冯永忠[3]探讨了错口丁坝的回流长度、回流与主流分界线及其最大宽度问题;李国斌等[4]研究了非淹没丁坝下游回流长度及最大回流宽度的影响因素;韩玉芳等[5]分析了丁坝回流长度与丁坝附近河床冲刷发展过程的变化关系;Ettema等[6-7]讨论了丁坝回流边线及分离区尺度问题;陈稚聪等[8]探讨了丁坝回流横向和纵向分区问题,分析了回流尺度及流量沿纵向的变化规律;郑艳等[9]研究了丁坝长度对回流长度的影响规律;马永军等[10-11]讨论了减小丁坝下游回流尺度的有效方法。然而,上述研究都是针对单式断面丁坝的,工程实践表明,当河道水位介于两级整治水位之间形成非淹没阶梯形丁坝时,下游回流规律将受两级丁坝几何尺度和水流条件的影响,较单式断面丁坝更为复杂,但目前相关研究还鲜有涉及。为此,本文将以非淹没阶梯形丁坝为例,探讨双级丁坝几何尺度和来流条件对回流规律的影响,研究结果可为工程设计提供参考。
1 数学模型及其验证 1.1 模型建立 1.1.1 基本方程本文应用三维浅水运动数值模拟开展研究,垂向采用分层二维计算方法,基本控制方程为:
| ${\rm{连续方程;}}\quad \partial u/\partial x + \partial v/\partial y + \partial w/\partial z = 0$ | (1) |
动量方程:
| $\begin{array}{l} \frac{{\partial u}}{{\partial t}} + u\frac{{\partial u}}{{\partial x}} + v\frac{{\partial u}}{{\partial y}} + w\frac{{\partial u}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial P}}{{\partial x}} - fv + \\ \frac{1}{\rho }\left( {\frac{{\partial {\tau _{xx}}}}{{\partial x}} + \frac{{\partial {\tau _{xy}}}}{{\partial y}} + \frac{{\partial {\tau _{xz}}}}{{\partial z}}} \right) = {A_x}\Delta u \end{array}$ | (2) |
| $\begin{array}{l} \frac{{\partial v}}{{\partial t}} + u\frac{{\partial v}}{{\partial x}} + v\frac{{\partial v}}{{\partial y}} + w\frac{{\partial v}}{{\partial z}} + \frac{1}{\rho }\frac{{\partial P}}{{\partial y}} + fu + \frac{1}{\rho }\\ \left( {\frac{{\partial {\tau _{yy}}}}{{\partial y}} + \frac{{\partial {\tau _{yx}}}}{{\partial x}} + \frac{{\partial {\tau _{yz}}}}{{\partial z}}} \right) = {A_y}\Delta v \end{array}$ | (3) |
| $P = {P_0} + \rho g\left( {H - z} \right)$ | (4) |
式中:x,y,z为笛卡尔坐标的3个方向;u,v,w分别为x,y,z向的流速分量;t为时间;ρ为水的密度;P为水压力;f为柯氏系数,f= 2Ωsinφ,Ω为地球自转角速度,φ为当地地理纬度;τxx,τxy,τxz,τyy,τyx,τyz分别为剪切应力张量的分量;Ax,Ay分别为x,y向的紊动扩散系数;Δ为拉普拉斯算子;P0为水表面处大气压力;g为重力加速度;H为水深。
根据线性k-ε紊流模型,剪切应力张量的分量τij可表示为:
| ${\tau _{ij}} = \rho \left[ {{v_t}\left( {\frac{{\partial {u_i}}}{{\partial {x_j}}} + \frac{{\partial {u_j}}}{{\partial {x_i}}}} \right) - \frac{2}{3}k{\delta _{ij}}} \right]\quad \quad {v_t} = {C_\mu }\frac{{{k^2}}}{\varepsilon }$ | (5) |
式中:νt为紊动黏滞系数;δij为Kronecker delta符号,当i=j时,δij=1,否则δij=0;k为紊动能,ε为紊动能耗散率,求解方程为:
| $\frac{{\partial k}}{{\partial t}} + {u_j}\frac{{\partial k}}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {v + \frac{{{v_t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + {P_k} - \varepsilon $ |
| ${P_k} = - \overline {{{u'}_i}{{u'}_j}} \partial \overline {{u_i}} /\partial {x_j}$ |
| $\frac{{\partial \varepsilon }}{{\partial t}} + {u_j}\frac{{\partial \varepsilon }}{{\partial {x_j}}} = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {v + \frac{{{v_t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \frac{\varepsilon }{k}\left( {{C_1}{P_k} - {C_2}\varepsilon } \right)$ |
模型中参数取值为:Cμ=0.09,C1=1.44,C2=1.92,σk=1.0,σε=1.3。
1.1.2 数值方法基本控制方程组采用有限体积法离散求解,平面为非结构化的三角形网格,垂向选用分层结构化网格。压力和速度场耦合计算采用SIMPLEC算法,代数方程组采用交替方向隐式迭代算法(ADI算法)和三对角矩阵算法(TDMA算法)求解,计算收敛准则为所有变量的最大无量纲残差小于10-5。
1.1.3 边界条件设定水槽左、右两岸均为陆边界,水流的法向分量恒为0;进口边界给定初始流速、紊动能及其耗散率;出口边界给定法向零梯度假定;固壁边界考虑壁面影响,将壁面应力加入方程并修正相应的边界系数和源项;采用VOF法计算自由水面。
1.1.4 计算参数计算中最大、最小时间步长分别取0.2和0.001 s;临界柯朗数取0.8;为避免水深为0或较小时出现计算机数值溢出或发散,设置了干湿单元临界值,干水深hd= 0.005 m,湿水深hw= 0.10 m,容许淹没水深hf = 0.05 m。
1.2 模型验证 1.2.1 水槽试验采用水槽试验资料进行模型验证,试验在重庆交通大学国家内河航道整治工程技术研究中心进行,整个循环装置包括水池、泵站、平水塔、量水堰、进水前池、矩形直道水槽、尾水闸门和循环水廊道,水槽长48 m、宽2 m、高1 m,其侧面与底面均采用混凝土抹面,底坡为5‰。丁坝布设在水槽左岸,丁坝轴线距水槽进口断面28 m,确保来流平顺并接近均匀流,距水槽出口20 m,使回流得以充分发展和衰减。丁坝采用双级阶梯形断面,一级丁坝长b1 =80 cm、高D1=15 cm,二级丁坝长b2=40 cm、高D2=35 cm,不考虑丁坝顶部宽度和上、下游边坡的影响,设计成顶宽10 cm的直立式丁坝,坝头为半圆形,各级丁坝均采用混凝土制作,并在表面涂上一层红漆(见图 1)。

|
图 1 阶梯形丁坝及流速测点布置(单位:cm) Figure 1 Arrangement of step-shaped spur dike and velocity measuring points (unit: cm) |
试验流量Q=190 L/s,尾门断面水深H0=0.35 m。流量采用量水堰控制。水位采用SCM60型测针观测,沿程布置了17个观测断面。流速采用Vectrino小威龙流速仪观测,共布置7个观测断面(CS1~CS7),丁坝轴线位于CS3,上游CS1~CS2断面距丁坝轴线分别为75和25 cm,下游CS4~CS7断面距丁坝轴线分别为25, 50, 100和150 cm。各断面沿宽度方向均布设11条测流垂线,垂线间距20 cm(近壁垂线距边壁约5 cm);流速采集的水深范围为4~31 cm,流速测点间距4.5 cm,其中一级丁坝顶部各垂线布置4个测点,其余各垂线布置7个测点,采样点位于流速仪正下方4 cm处。
数模计算沿水深方向等分为9层,平面采用三角形网格,全计算域共252 045个单元、14 475个节点,丁坝区域计算网格边长2 cm,其余区域网格边长逐渐过渡至8 cm。
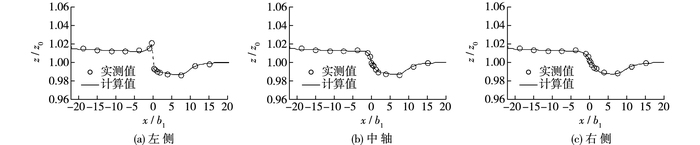
1.2.2 水位验证选择水槽左侧、中轴和右侧3条纵向水面线进行验证,验证结果见图 2,图中横坐标为采用沿程距离x与一级丁坝长度b1之比的相对沿程距离,纵坐标为采用当地水位z与尾门断面水位z0之比的相对水位。结果显示,丁坝所在的左侧上游自由水面逐渐升高,至坝前达到最大值,坝后水面线快速下降,此后缓慢上升,至x/b1=15处基本保持稳定;中轴和右侧水面线变化基本一致,丁坝断面(x/b1=0)上游水位缓慢下降,至丁坝前缘受束流影响水位急剧下降,过丁坝后水流扩散,水面逐渐上升,直至保持稳定。从验证效果看,计算和实测水面线总体吻合,水位非常接近。
|
图 2 水位验证 Figure 2 Verification of water level |
(1) 平面流速分布 根据水槽试验测流情况,图 3给出了距槽底0.78H层和0.43H层(H为丁坝断面平均水深)的流场分布对比,可见,计算和实测流场的流速分布形态及大小较接近,均揭示了坝头分离流和坝后回流。

|
图 3 平面流场验证 Figure 3 Verification of plane flow field |
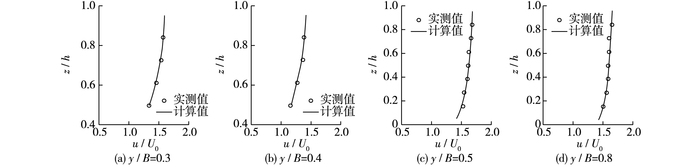
(2) 垂线流速分布 限于篇幅,图 4仅给出了丁坝断面(CS3)上4条代表垂线的纵向流速垂线分布验证情况,图中y/B (水槽宽度B=2 m)为距左侧边壁的相对距离,u/U0为采用尾门断面平均流速无量纲化后的流速。验证结果显示,计算与实测流速大小及垂线分布均较为吻合。
|
图 4 纵向流速垂线分布验证 Figure 4 Vertical distribution verification of longitudinal velocity |
综上水位和流场验证结果,表明本文数学模型合理,结果可靠,可用于下一步研究。
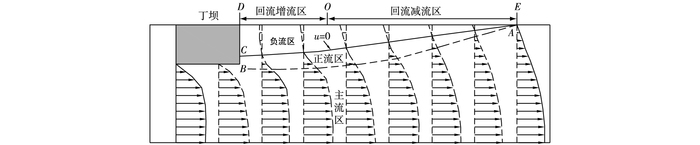
2 结果与讨论 2.1 丁坝回流区界定研究[8]表明,丁坝回流区可进一步划分为正流区和负流区(见图 5),划分方法如下:回流发生并稳定后存在一条曲线AB,此线内侧区域为回流区,外侧区域为主流区,主流区流量始终等于上游来流量;回流区内的纵向流速有正有负,正、负向流速交界曲线AC的纵向流速为0,以曲线AC为界,内侧区域称为负流区,外侧区域称为正流区,正、负流区的纵向流量绝对值相等而方向相反,处于自成体系的动平衡状态。在回流区,前段(DO区段)为回流增流区,回流流量沿程逐渐增加,后段(OE区段)为回流减流区,回流流量沿程逐渐减小,增流区和减流区的分界点O处回流流量最大。
|
图 5 丁坝回流区划分示意 Figure 5 Partition of backflow region |
定义一级丁坝相对长度ε1=b1/B、二级丁坝相对长度ε2=b2/B、一级丁坝相对高度ψ1=D1/H0。回流参数包括回流长度、回流宽度、正负流区宽度比、回流曲线形态和回流流量等,下面基于水流数学模型的计算结果(计算工况见表 1),探讨阶梯形丁坝几何尺度ε1, ε2, ψ1和水流条件Fr对上述参数的影响规律,成果分析时在丁坝下游回流区每隔0.25 m布置一个统计断面,沿断面方向每隔0.10 m布置一条统计垂线,各垂线有9个流速点据。
| 表 1 水流数学模型计算工况 Table 1 Calculation condition of flow mathematical model |
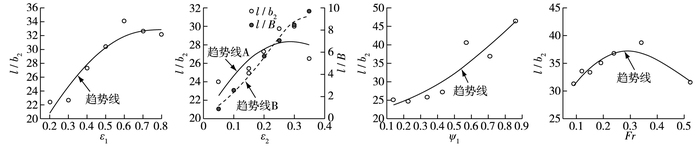
图 6给出了ε1,ε2,ψ1和Fr对无量纲回流长度l/b2(l为回流长度)的影响规律。结果表明:① l/b2(或l/B)随ε1和ε2均呈递增变化,ε1,ε2越大,l/b2递增变化速度越缓,回流长度一般可达二级丁坝长度的20~30倍;② l/b2随ψ1也呈递增变化,ψ1越大,l/b2递增变化越明显,这主要因为一级丁坝长度大于二级丁坝,其高度增大后对坝后回流尺度的影响将更为突出;③由于ε1,ε2和ψ1的变化将改变河道糙率,丁坝回流长度与河道糙率有关[4],因而l/b2将发生相应变化;④ l/b2随Fr呈先增大后减小的趋势,l/b2最大值出现在Fr=0.35附近,比较而言,Fr对回流长度的影响较ε1,ε2,ψ1更不明显;⑤阶梯形丁坝回流长度随丁坝坝长的增大而增大、Fr对回流长度影响较小等变化规律与现有单式断面丁坝的研究结论[12]基本一致。
|
图 6 回流长度随影响因素的变化 Figure 6 Change of backflow region length with influencing factors |
图 7给出了回流宽度参数(回流宽、正流宽和负流宽)最大值及平均值随ε1,ε2,ψ1和Fr的变化情况。图中显示:①回流宽、正流宽和负流宽的最大值及平均值随ε1,ε2,ψ1和Fr的变化趋势总体一致;②当ε1≤0.6时,回流宽度参数随ε1缓慢递增,当ε1>0.6时,回流宽度参数随ε1基本不变,最大回流宽约为二级丁坝宽度的1.5~2.0倍,与单式断面丁坝的研究结论[9]接近;③回流宽度参数b/B和b/b2随ε2呈现出相反的变化趋势,ε2越大,b/B越大,而b/b2越小,说明回流宽度随二级丁坝长度的增大而增大,但相对增幅逐渐递减;④当ψ1≤0.45时,回流宽度参数随ψ1基本不变,当ψ1>0.45时,回流宽度参数随ψ1先增大后减小,b/b2的最大值出现在ψ1=0.70附近;⑤最大回流宽度随Fr呈先增大后减小的趋势变化,平均回流宽度随Fr的变化相对较不明显。

|
图 7 回流宽度随影响因素的变化 Figure 7 Change of backflow region width with influencing factors |
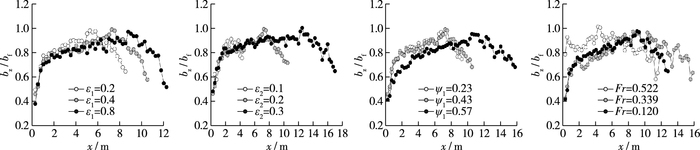
图 8给出了典型计算工况下回流正、负流区宽度比bz/bf随ε1,ε2,ψ1和Fr的变化趋势(图中bz和bf分别为各统计断面的回流正流区宽度和负流区宽度),图中显示:① bz/bf沿程变化曲线总体为上凸状,多呈先增大、后基本稳定、再减小的变化过程;② bz/bf随ε2变化的波动相对较小,而随ε1,ψ1和Fr的波动相对略大;③ bz/bf值一般小于1.0,说明负流区宽度相对更大,尤其在靠近丁坝的部位,负流区宽度可达正流区宽度的2.5倍。
|
图 8 正、负流区宽度比随影响因素的变化 Figure 8 Change of positive velocity region width and negative velocity region width with influencing factors |
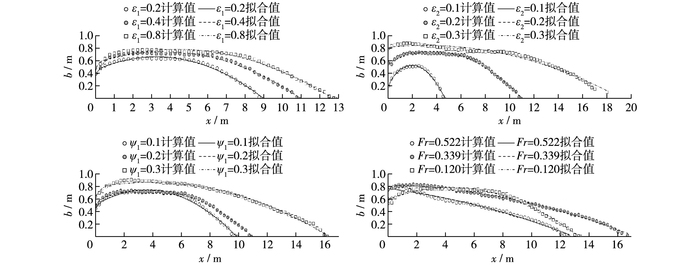
图 9给出了典型计算工况下的回流曲线形态随ε1, ε2, ψ1和Fr的变化趋势(图中x为沿程距离,b为各统计断面的回流宽度),可见:①与单式断面丁坝回流曲线形态[8]类似,阶梯形丁坝的回流曲线也呈纺锤状;②随着ε1和ψ1的增大,回流曲线最大宽度变化不大,但回流长度逐渐增大,曲线形态逐渐被拉长;③不同ε2下的回流曲线差别明显,ε2越大,回流曲线长度和宽度也越大,说明ε2对回流曲线形态影响较大;④由于Fr对回流长度和宽度的影响均较小,回流曲线形态也随Fr的变化不大。
|
图 9 回流曲线形态随影响因素的变化 Figure 9 Change of backflow curve shape with influencing factors |
根据沿程统计断面的垂线及流速点布置情况,可计算各垂线的分条流量Qi= BiHiUi,其中为Bi, Hi, Ui分别为分条宽度(Bi=0.10 m)、平均水深和纵向垂线平均流速,从丁坝对岸的右侧向丁坝侧分别计算分条流量Qi。当分条流量之和ΣQi等于上游来流量Q时,该垂线即为统计断面的回流区边界所在位置(实际计算时一般需由相邻两垂线线性内插ΣQi=Q的具体位置);由于回流区正向流动和负向流动的流量之和为0,且各断面流量是闭合的,假定Qi>0的分条流量和为Q1,则回流流量QH = Q1-Q。根据上述方法,可计算各统计断面的回流流量。
图 10给出了典型计算工况下相对回流流量QH/Q的沿程变化情况,结果表明:① QH/Q总体随ε1,ε2和ψ1的增大而增大,随Fr的增大而减小,各工况下QH/Q最大值多在0.04~0.10范围内变化,说明回流流量一般小于来流量的10%;②紧邻丁坝下游端回流流量逐渐增大,为回流增流区,当达到最大值后,回流流量逐渐减小,为回流减流区,增流区和减流区的分界点沿程位置随ε1, ε2, ψ1和Fr的变化范围分别为(2.37~3.38), (1.24~4.64), (2.74~3.14)和(1.24~3.13)倍水槽宽度,说明ε1和ψ1对分界点沿程位置的影响较小,而ε2和Fr的影响较大;③回流流量沿程分布呈右偏的不对称曲线,增流区回流流量变化相对缓慢,而减流区变化相对剧烈。

|
图 10 回流流量随影响因素的变化 Figure 10 Change of circumfluence flow with influencing factors |
阶梯形丁坝是常见的航道整治建筑物,应用三维水流数学模型并在模型验证的基础上,研究了阶梯形丁坝几何尺度及来流条件对回流规律的影响,主要认识如下:
(1) 阶梯形丁坝回流长度随一级丁坝相对长度ε1及高度ψ1、二级丁坝相对长度ε2均呈递增趋势,随弗劳德数Fr呈先增后减的变化趋势,回流长度最大值出现在Fr=0.35附近。
(2) 回流宽、正流宽和负流宽的特征值随ε1, ε2, ψ1和Fr的变化趋势总体一致;ε1≤0.6时回流宽度缓慢递增,此后基本不变;回流宽度随ε2的增大而增大,但相对增幅逐渐递减;ψ1≤0.45时回流宽度基本不变,ψ1>0.45时回流宽度随ψ1先增大后减小;最大回流宽度随Fr呈先增大后减小的趋势变化,平均回流宽度随Fr的变化相对较不明显。
(3) 回流正、负流区宽度比沿程变化曲线总体为上凸状,多呈先增大、后基本稳定、再减小的变化过程,负流区宽度相对较大,在靠近丁坝部位可达正流区宽度的2.5倍。
(4) 阶梯形丁坝的回流曲线呈纺锤状,ε1和ψ1主要影响回流曲线长度,ε2影响回流曲线的整体形态,而Fr对回流曲线形态影响较小。
(5) 回流流量一般小于上游来流量的10%,沿程分布曲线不对称,增流区回流流量变化相对缓慢,而减流区变化相对剧烈。
| [1] |
周冠伦, 荣天富, 刘书伦, 等. 航道工程手册[M]. 北京: 人民交通出版社, 2004: 687-688. ( ZHOU Guanlun, RONG Tianfu, LIU Shulun, et al. Waterway engineering handbook[M]. Beijing: People's Commumication Press, 2004: 687-688. (in Chinese))
|
| [2] |
周鑫靖. 非淹没双级复式断面丁坝三维水流特性研究[D]. 重庆: 重庆交通大学, 2016. (ZHOU Xinjing. Three-dimensional flow characteristics of non-submerged spur dike with two-stage compound section[D]. Chongqing: Chongqing Jiaotong University, 2016. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10618-1016163390.htm
|
| [3] |
冯永忠. 错口丁坝回流尺度的研究[J]. 河海大学学报, 1995, 23(4): 69-76. ( FENG Yongzhong. Study on recirculating flow range caused by groins lying alternately[J]. Journal of Hohai University, 1995, 23(4): 69-76. (in Chinese)) |
| [4] |
李国斌, 韩信, 傅津先. 非淹没丁坝下游回流长度及最大回流宽度研究[J]. 泥沙研究, 2001(3): 68-73. ( LI Guobin, HAN Xin, FU Jinxian. Study on the length and maximum width of the circulating region caused by a dike[J]. Journal of Sediment Research, 2001(3): 68-73. (in Chinese)) |
| [5] |
韩玉芳, 陈志昌. 丁坝回流长度的变化[J]. 水利水运工程学报, 2004(3): 33-36. ( HAN Yufang, CHEN Zhichang. Variation of re-circulation length of spur dikes[J]. Hydro-Science and Engineering, 2004(3): 33-36. (in Chinese)) |
| [6] |
ETTEMA R, MUSTE M. Scale effects in flume experiments on flow around a spur dike in flat bed channel[J]. Journal of Hydraulic Engineering, 2004, 130(7): 635-646. DOI:10.1061/(ASCE)0733-9429(2004)130:7(635) |
| [7] |
SHARMA K, MOHAPATRA P K. Separation zone in flow past a spur dyke on rigid bed meandering channel[J]. Journal of Hydraulic Engineering, 2013, 138(10): 897-901. |
| [8] |
陈稚聪, 黑鹏飞, 丁翔. 丁坝回流分区机理及回流尺度流量试验研究[J]. 水科学进展, 2008, 19(5): 613-617. ( CHEN Zhicong, HEI Pengfei, DING Xiang. Division and flow scale investigation of circulation zone around spur dike[J]. Advances in Water Science, 2008, 19(5): 613-617. (in Chinese)) |
| [9] |
郑艳, 魏文礼, 刘玉玲. 丁坝长度对回流长度影响的数值模拟研究[J]. 沈阳农业大学学报, 2014, 45(2): 195-199. ( ZHENG Yan, WEI Wenli, LIU Yuling. Influence of spur-dike length on the recirculation scale by numerical simulation[J]. Journal of Shenyang Agricultural University, 2014, 45(2): 195-199. (in Chinese)) |
| [10] |
马永军, 陈稚聪, 丁翔. 控制和减小丁坝下游回流影响的实验[J]. 清华大学学报(自然科学版), 2003, 43(8): 1096-1099. ( MA Yongjun, CHEN Zhicong, DING Xiang. Controlling recirculating regions downstream of spur dikes[J]. Journal of Tsinghua University(Science and Technology), 2003, 43(8): 1096-1099. (in Chinese)) |
| [11] |
马永军, 陈稚聪, 丁翔. 吸、喷水法减小丁坝下游回流尺度的试验研究[J]. 水科学进展, 2003, 14(6): 763-768. ( MA Yongjun, CHEN Zhicong, DING Xiang. Experimental study on reducing the size of circulating region in the downstream of spur dikes[J]. Advances in Water Science, 2003, 14(6): 763-768. (in Chinese)) |
| [12] |
窦国仁. 丁坝回流及其相似律的研究[J]. 水利水运科技情报, 1978(3): 1-24. ( DOU Guoren. An investigation on the whirlpool flow and its similarity laws[J]. Information of Hydro-Science and Engineering, 1978(3): 1-24. (in Chinese)) |
2. Key Laboratory of Hydraulic and Waterway Engineering of the Ministry of Education, Chongqing Jiaotong University, Chongqing 400074, China;
3. Chongqing Information and Communication Consulting and Design Institute Co., Ltd., Chongqing 400041, China
 2017
2017 