截至2011年底,我国已建成各类水库大坝98 002座[1],是当今世界拥有水库大坝最多的国家。这些堤坝工程极大地促进了我国社会经济发展,然而一旦发生溃坝事故,将造成不可估量的社会经济损失及惨重的人员伤亡。近年来,国内外专家学者对溃坝问题给予了高度重视并开展了一系列科研工作[2-5],如:美国1996年启动的国家大坝安全计划(NDSP),欧盟自1998年起连续启动的CADAM,IMPACT以及FLOODsite项目,芬兰1999年启动实施的RESCDAM项目等,并在试验的基础上提出了“Headcut”溃坝溯源冲蚀发展机理。结合我国黏性土坝自身的特点,南京水利科学研究院开展了大量现场原型试验和室内小尺度物理模型试验研究[6],对溃坝机理进行了有效发展和完善。相关成果表明,土坝漫顶时,在相当长的时间内并不会形成贯通坝体上下游的大溃口,而在坝体下游坡面的中上部易形成首个冲刷坑,造成初始冲刷并使得水流结构发生相应的改变,之后在其下部形成第二级冲坑,各冲坑以“跌坎剪剥式(Headcut)”冲蚀方式向上游逐步推进。Powledge[7]和李云[8]等亦分别从理论分析和数值模拟的角度阐述了类似观点,他们认为溃坝发生时,初始冲坑可能发生在下游坡面的任意位置,尤其坝肩附近由于坝体体型突变而导致的漫顶水流挑流落点处。
由此可见,溃坝跌坎水流是黏性土坝漫顶溃决过程中的典型代表性水流型式之一,然而以往对于溃决水流的模拟大多假设坝体瞬间全部溃决或者是瞬间局部溃决,且研究内容主要侧重于土坝溃决峰值流量预测以及下游洪水演进问题[9-12], 对溃坝过程中坝体区域的水流特性缺乏系统的研究;此外,黏性土坝漫顶溃决涉及多学科交叉,过程极其复杂,考虑水土耦合从整体上进行统一模拟具有极大的难度和不确定性。鉴于此,本文针对溃坝发展过程中的典型溃口形态,采用三维数值模拟技术对其水动力特性进行研究,全面揭示水流冲蚀主动力,进而从该角度对黏性土坝溯源蚀退机理的发展和完善提供理论基础。
1 数学模型的建立 1.1 水流控制方程组计算流体动力学无论具体采用何种形式,都建立在流体力学基本控制方程——连续性方程、动量方程和能量方程的基础之上,必须遵循3个基本物理学原理:质量守恒、牛顿第二定律以及能量守恒。在黏性土坝漫顶溃决的整个发生发展过程中,机械能与内能的相互转化可以忽略不计,因此在相关水力学问题研究中,主要满足连续性方程和动量守恒方程即可。本文在建模时采用“FAVOR”技术,即在连续性方程和动量守恒方程中加入含有面积和体积分数的参数,表示如下。
| ${\rm{连续性方程}}:\frac{{\partial \left( {u{A_x}} \right)}}{{\partial x}} + \frac{{\partial \left( {v{A_y}} \right)}}{{\partial y}} + \frac{{\partial \left( {w{A_z}} \right)}}{{\partial z}} = 0$ | (1) |
| ${\rm{动量守恒方程}}:\left\{ {\begin{array}{*{20}{l}} {\frac{{\partial u}}{{\partial t}} + \frac{1}{{{V_{\rm{F}}}}}\left( {u{A_x}\frac{{\partial u}}{{\partial x}} + v{A_y}\frac{{\partial u}}{{\partial y}} + w{A_z}\frac{{\partial u}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial x}} + {G_x} + {f_x}}\\ {\frac{{\partial v}}{{\partial t}} + \frac{1}{{{V_{\rm{F}}}}}\left( {u{A_x}\frac{{\partial v}}{{\partial x}} + v{A_y}\frac{{\partial v}}{{\partial y}} + w{A_z}\frac{{\partial v}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial y}} + {G_y} + {f_y}}\\ {\frac{{\partial w}}{{\partial t}} + \frac{1}{{{V_{\rm{F}}}}}\left( {u{A_x}\frac{{\partial w}}{{\partial x}} + v{A_y}\frac{{\partial w}}{{\partial y}} + w{A_z}\frac{{\partial w}}{{\partial z}}} \right) = - \frac{1}{\rho }\frac{{\partial p}}{{\partial z}} + {G_z} + {f_z}} \end{array}} \right.$ | (2) |
式中:ρ为流体密度;p为压力;t为时间;u,v,w为速度矢量在x,y,z方向上的分量;Ax,Ay,Az表示x,y,z方向可以流动的面积分数;VF为可流动的体积分数;G为重力项;fx,fy,fz为3个方向的黏滞力。
1.2 RNG k-ε紊流模型RNG k-ε模型是针对标准k-ε模型在模拟强旋流或带有弯曲壁面的流动时出现失真现象而提出的,在模拟冲击射流、分离流、二次流等复杂流动时具有较大的优势,考虑到溃坝跌坎冲射水流的强紊动特性,本文在数值计算中采用该模型对Navier-Stokes控制方程进行封闭。同样在模型中加入表征相应体积、面积分数的参数,则直角坐标系下的湍动能kT和耗散率εT的输运方程为:
| $\frac{{\partial {k_{\rm{T}}}}}{{\partial t}} + \frac{1}{{{V_{\rm{F}}}}}\left( {u{A_x}\frac{{\partial {k_{\rm{T}}}}}{{\partial x}} + v{A_y}\frac{{\partial {k_{\rm{T}}}}}{{\partial y}} + w{A_z}\frac{{\partial {k_{\rm{T}}}}}{{\partial z}}} \right) = {P_{\rm{T}}} + {G_{\rm{T}}} + {D_{\rm{T}}} - {\varepsilon _{\rm{T}}}$ | (3) |
| $\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial t}} + \frac{1}{{{V_{\rm{F}}}}}\left( {u{A_x}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial x}} + v{A_y}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial y}} + w{A_z}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial z}}} \right) = \frac{{{C_{{\rm{1s}}}}{\varepsilon _{\rm{T}}}}}{{{k_{\rm{T}}}}}({P_{\rm{T}}} + {C_{3{\rm{s}}}}{G_{\rm{T}}}) + {D_\varepsilon } - {C_{2{\rm{s}}}}\frac{{\varepsilon _{\rm{T}}^2}}{{{k_{\rm{T}}}}}$ | (4) |
式中:kT为紊动能;PT为由速度梯度引起的紊动能产生项;GT为浮力引起的紊动能产生项;DT和Dε为紊动扩散项;εT为紊动耗散率;C1s, C2s和C3s均为无量纲系数,在模型中,C1s取1.44,C2s取1.92,C3s取0.2。
速度梯度引起的紊动项PT由式计算,如下:
| ${P_{\rm{T}}} = {C_{\rm{s}}}\frac{\mu }{{\rho {V_{\rm{F}}}}}\left\{ {\begin{array}{*{20}{l}} {2{A_x}{{\left( {\frac{{\partial u}}{{\partial x}}} \right)}^2} + 2{A_y}{{\left( {\frac{{\partial v}}{{\partial y}}} \right)}^2} + 2{A_z}{{\left( {\frac{{\partial w}}{{\partial z}}} \right)}^2} + \left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial u}}{{\partial x}}} \right)\left[ {{A_x}\frac{{\partial v}}{{\partial x}} + {A_y}\frac{{\partial u}}{{\partial y}}} \right] + }\\ {\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial w}}{{\partial x}}} \right)\left( {{A_z}\frac{{\partial u}}{{\partial z}} + {A_x}\frac{{\partial w}}{{\partial x}}} \right) + \left( {\frac{{\partial v}}{{\partial z}} + \frac{{\partial w}}{{\partial y}}} \right)\left( {{A_z}\frac{{\partial v}}{{\partial z}} + {A_y}\frac{{\partial w}}{{\partial y}}} \right)} \end{array}} \right\}$ | (5) |
式中:Cs为参数,默认取1;μ为动力黏滞系数。
浮力引起的紊动项GT由式计算,如下:
| ${G_{\rm{T}}} = - {C_{\rm{o}}}\frac{\mu }{{{\rho ^3}}}\left( {\frac{{\partial \rho }}{{\partial x}}\frac{{\partial p}}{{\partial x}} + \frac{{\partial \rho }}{{\partial y}}\frac{{\partial p}}{{\partial y}} + \frac{{\partial \rho }}{{\partial z}}\frac{{\partial p}}{{\partial z}}} \right)$ | (6) |
式中:p为压力; Co为紊动参数。
扩散项DT和Dε的表达式分别如下所示:
| ${D_{\rm{T}}} = \frac{1}{{{V_{\rm{F}}}}}\left\{ {\frac{\partial }{{\partial x}}\left( {{\upsilon _k}{A_x}\frac{{\partial {k_{\rm{T}}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\upsilon _k}{A_y}\frac{{\partial {k_{\rm{T}}}}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{\upsilon _k}{A_z}\frac{{\partial {k_{\rm{T}}}}}{{\partial z}}} \right)} \right\}$ | (7) |
| ${D_\varepsilon } = \frac{1}{{{V_{\rm{F}}}}}\left\{ {\frac{\partial }{{\partial x}}\left( {{\upsilon _\varepsilon }{A_x}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial x}}} \right) + \frac{\partial }{{\partial y}}\left( {{\upsilon _\varepsilon }{A_y}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial y}}} \right) + \frac{\partial }{{\partial z}}\left( {{\upsilon _\varepsilon }{A_z}\frac{{\partial {\varepsilon _{\rm{T}}}}}{{\partial z}}} \right)} \right\}$ | (8) |
式中:υk和υε为紊动扩散系数,根据运动黏滞系数υT而定,其中υT可表示为:
| ${\upsilon _{\rm{T}}} = {C_{\rm{u}}}k_{\rm{T}}^2/{\varepsilon _{\rm{T}}}$ | (9) |
式中:Cu默认取0.085。计算过程中对εT进行严格控制,避免造成与实际不符的巨大紊动能耗散。
1.3 数值计算方法采用有限差分法对控制方程进行离散,在空间上形成三维交错网格,将速度和面积分数定义在网格边界面中心,其他变量如压强、密度、流体黏度等定义在控制体中心。对流项采用一阶迎风离散格式,黏性项采用标准的中心差分离散格式。将控制方程离散为代数方程之后,首先引入一个中间速度量,不考虑下一时刻压力场对速度场产生的影响,引入当前时刻的压力修正值,通过求解动量方程获得中间速度,再将由动量方程离散出来的相关关系代入连续方程中,生成含有压力修正值的泊松方程。
GMRES算法计算精度高,收敛速度快且不易发散,因此本文选用该算法进行数值求解计算。壁面采用无滑移边界条件,近壁区域采用数学函数近似模拟,且由速度梯度产生的黏性剪切应力通过加入面积分数参数来考量,自由液面的追踪采用VOF(Volume of Fluid)方法来实现。
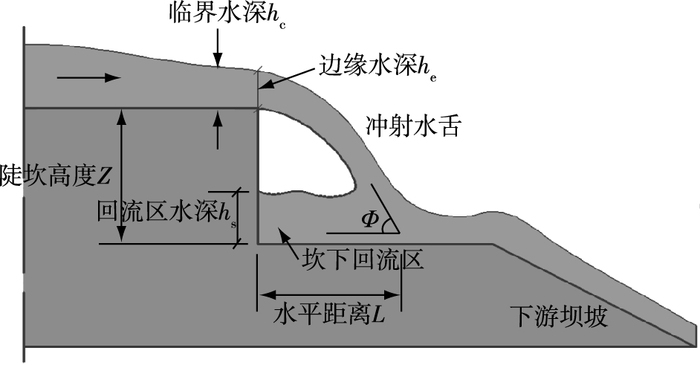
1.4 计算区域及边界条件设置溃坝发展过程中典型溃口形态见图 1。数学模型针对图 1所示的黏性土坝典型溃决水流开展研究,基于对众多试验现象的观测,将其概化如图 2所示。

|
图 1 黏性土坝漫顶溃决现场原型试验(坝高9.7 m) Figure 1 Prototype test of clayey soil dam failure due to overtopping(dam height: 9.7 m) |
|
图 2 溃坝跌坎水流结构示意 Figure 2 Schematic diagram of headcut flow structure of dam-break |
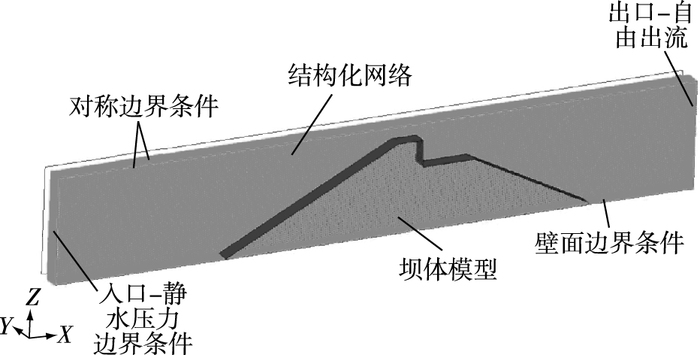
为方便利用前期开展的物理模型试验[13]进行验证,计算模型中取坝体高度0.2 m;上、下游原始坡度1:2;在坝体下游坡面中上部设不同高度的垂直跌坎;坝前水库模拟长度取0.5 m,以保证水位充分稳定;坝后0.44 m处设置为出口,减小出口段对坝体水流的影响。模型计算区域及网格划分如图 3所示,为了最大限度保证计算精度,整个计算域采用均一结构化网格进行划分,网格长宽比1:1,只在跌坎处等重点部位进行局部加密,最大网格尺寸0.002 5 m,总体网格数量为(120~170)万。
|
图 3 数值模拟计算区域及网格划分 Figure 3 Numerical simulation region and mesh generation |
数模计算时,上游入口采用静水压力边界条件;下游出口则采用自由出流边界条件,对出口水流不做过多限制;模型底部采用不可滑移壁面边界条件;在沿坝轴线方向两侧设置为对称边界条件,即边界上没有不稳定的特性和剪切存在。
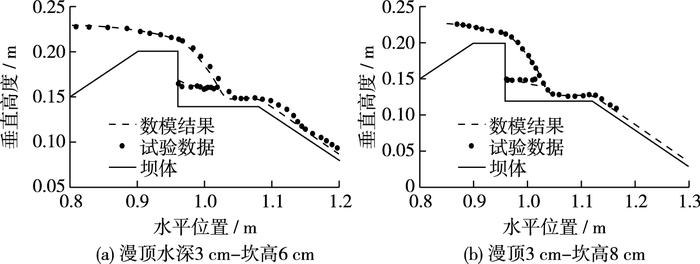
1.5 模型验证溃坝水流流经跌坎,由于体型突变,形成冲射水流对下游坝面造成冲刷。前期通过物理模型对溃坝典型水流进行了初步试验研究,将数模计算结果与模型试验结果进行对比分析,如图 4~5所示。从图 4~5可见,数模计算结果(坝顶、坎后坝坡水面线以及坝顶水流流速)与物模成果基本一致,仅局部稍有差异,鉴于溃坝跌坎水流紊动强烈、结构复杂,可认为所建数学模型对溃坝跌坎水流进行了准确模拟,具备了可靠的计算精度。
|
图 4 水面线对比验证 Figure 4 Contrast and verification of the water surface line |

|
图 5 坝顶平均流速对比验证 Figure 5 Contrast and verification of the mean flow velocity on dam crest |
跌坎冲射水流是黏性土坝溃决发展过程中的代表性水流结构,对其水力特性开展研究可从根本上了解掌握坝体形态的发展演变过程,具有重大的科研价值。
2.1 数模计算工况本文针对不同跌坎高度和不同漫顶水深工况开展全面三维数值模拟,对漫顶跌坎水流的冲刷主动力进行细致研究,从而为深入了解掌握黏性土坝溃决演变过程奠定基础,具体的数模计算工况如表 1所示。
| 表 1 数模计算工况 Table 1 Numerical calculation conditions |
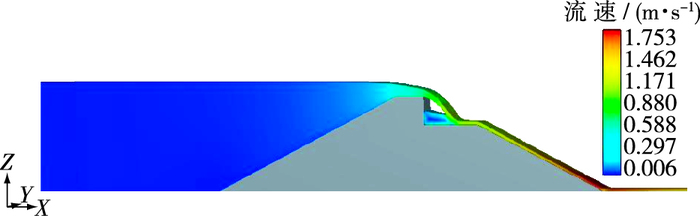
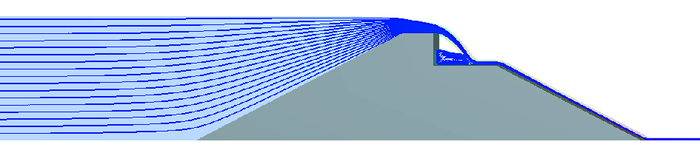
图 6为跌坎水流整体流场结构,图 7为漫顶冲射水流的流线分布情况。
|
图 6 跌坎水流整体流场结构(S3工况) Figure 6 Flow structure of headcut flow (S3 condition) |
|
图 7 跌坎冲射水流流线分布(S3工况) Figure 7 Streamline distribution of headcut flow (S3 condition) |
从图 6可见:①坝体上游库水位基本不变,在到达坝顶前缘时开始有明显的跌落现象,且漫顶水深在坝顶继续降低;②在冲射水流落点上游侧并非充满水,而是将形成一定深度的坎下回流区,这与试验结果完全一致;③在回流区内存在漩涡水流结构,使得水域中心位置流速稍小,且在冲射主流与落点上游侧水域之间存在较为明显的高速水流与低速水流的剪切层;④坎后下游坡面水流水面线较为光滑,水流流速沿程迅速增大,然而在坝址处由于坝体体型突变,存在局部流速减小区域。
由图 7可见:①水流流线在库区分布较为均匀,接近坝体时,受坝体的阻挡作用出现流线弯转,并在坝顶处汇集;②跌坎落点上游侧环状流线结构表明该处存在明显的漩涡水流结构。
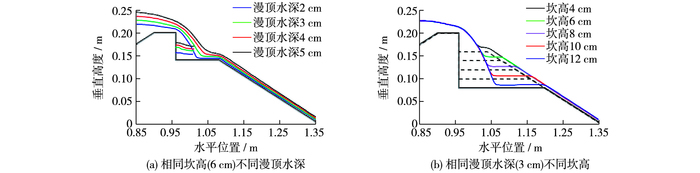
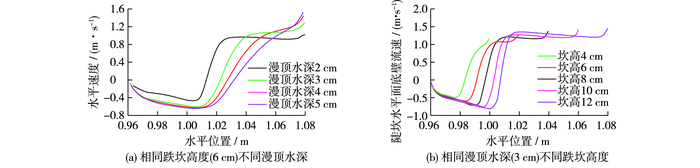
2.3 跌坎冲射水流水面线分布图 8(a)为同一跌坎高度下不同漫顶水深工况的水面线分布情况,从中可以看出:①水流流经跌坎形成冲射水流直接冲击跌坎水平面,并在落点上游侧形成具有一定深度的坎下回流区;②对于不同漫顶水深,冲射水平距离(冲射水流落点距跌坎底部的距离)和回流区水深都随漫顶水深的增大而增加;③在坝顶和坎后坡面,坝面水深沿程逐渐下降,并均随漫顶水深的增加而增大。图 8(b)为不同坎高工况下的坝面水面线分布情况,可见:①坝顶水面线分布基本保持一致,说明跌坎高度对于坝顶水流形式影响不大;②冲射水流空中轨迹具有较大的相似性,落点位置随着坎高的增加而逐渐增大;③不同跌坎高度下,坎后坝面水深沿程变化情况较为相似。
|
图 8 不同工况跌坎冲射水流水面线分布 Figure 8 Water surface line distribution under different conditions |
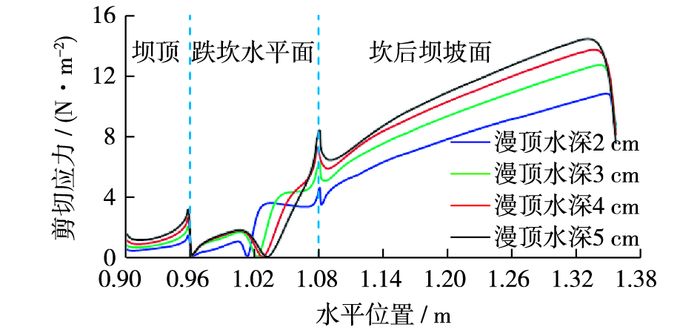
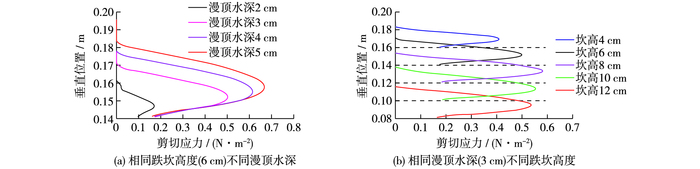
漫顶溃决水流产生的壁面剪切应力是坝体产生冲坑及侵蚀破坏的直接原因,图 9绘制了相同坎高(6 cm)不同漫顶水深工况下坝面剪切应力分布情况。从中可以看出:①剪切应力在坝顶上游坝肩位置存在略减小趋势,之后沿程迅速增大,并且在坝顶下缘的坝肩处存在剪切应力极大值;②在跌坎水平面水流落点两侧分别出现了剪切应力极大值,剪切应力分布呈现“双峰”特征,相比而言下游侧的剪切应力峰值较大。在冲射水流落点上游侧,首先出现剪切应力极大值,随后逐渐减小,至跌坎底部时相应剪切应力很小;③在跌坎水平面与下游坝坡连接部位由于体型变化再次出现剪切应力的极大值,而若水流落点距离连接部位较近,则两个剪切应力极值有可能“合并”成为较大极值,如漫顶水深4和5 cm工况所示;④坎后坡面剪切应力分布较为规则,沿程逐渐增大,而在坝趾处受坝体体型变化出现剪切应力极小值;⑤尽管在不同坝体区域存在不同的剪切应力分布形式,然而随着漫顶水深的增大,坝面剪切应力整体呈现增大的趋势,且在坝坡中下部增幅逐渐加大。
|
图 9 相同坎高(6 cm)不同漫顶水深坝面剪切应力分布 Figure 9 Shear stress distribution under different overtopping depths |
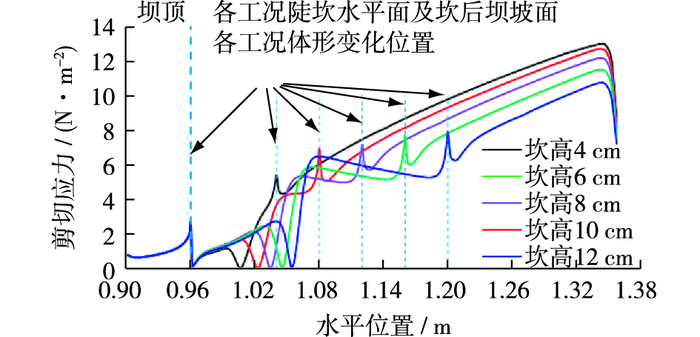
本文亦对不同跌坎高度工况进行了数值模拟,图 10为相同漫顶水深(3 cm)不同跌坎高度工况下的坝面剪切应力分布。由图 10可以看出:①各工况坝顶剪切应力分布基本相同,在坝顶上游坝肩位置出现小范围减小趋势,之后剪切应力沿程迅速增大,并在坝顶下缘位置出现极大值;②不同坎高将导致不同冲射水流落点位置,冲射落点水平距离(落点距跌坎根部的水平距离)随跌坎高度的增大而增大;③冲射水流在落点两侧同样形成剪切应力极大值,呈现“双峰”型式,随着跌坎高度的增大,水流落点两侧的剪切应力极值也逐渐增大。然而在跌坎根部附近各工况剪切应力分布基本一致,剪切应力值均较小;④对于同一跌坎高度,坎后坡面剪切应力依然沿程增大,然而对于不同坎高工况,坎后剪切应力随着坎高的增大整体呈减小趋势。
|
图 10 相同漫顶水深(3 cm)不同跌坎高度下坝面剪切应力分布 Figure 10 Shear stress distribution under different headcut heights |
图 11(a)为相同跌坎高度不同漫顶水深工况下跌坎垂直面剪切应力分布,由图可见:①在跌坎垂直面上,剪切应力呈“单峰”分布,在垂直面中部剪切应力较大,跌坎底部及水域上部剪切应力较小;②不同漫顶水深工况下,随着漫顶水深的增大,垂直壁面上剪切应力最大值逐渐增大,最大剪切应力作用点位置也逐渐上移;③随着漫顶水深的不断增大,尽管垂直壁面剪切应力整体呈现增大的趋势,然而峰值变幅存在逐渐减小的趋势。图 11(b)为相同漫顶水深不同跌坎高度工况下,跌坎垂直壁面剪切应力的分布,由图可见:①坝体跌坎垂直面上剪切应力均呈“单峰”分布,自跌坎底部沿垂直方向剪切应力先增大后减小;②在跌坎高度逐渐增大的过程中,垂直壁面剪切应力峰值存在先增大后减小的趋势,这一规律表明:在跌坎逐渐加深的过程中存在一定的限值,当坎高达到这一高度后,水流对于跌坎垂直面的作用力反而会越来越小。
|
图 11 不同工况下跌坎垂直壁面剪切应力分布 Figure 11 Shear stress distribution on vertical wall surface |
跌坎垂直面上的剪切应力分布直接关系到坝体纵向冲蚀发展过程,对比图 9,10和11可知,跌坎冲射水流在水平壁面上产生的最大水流剪切应力比垂直面上剪切应力要大很多,有的工况甚至可达几十倍,由此可初步推断黏性土坝漫顶溃决过程中各级跌坎主要以“台阶水平面刷深下切”的方式进行合并。
2.5 跌坎底壁水平流速分布跌坎水平面底壁流速分布直接反映了坎下回流区的水流结构特性,图 12(a)为相同跌坎高度不同漫顶水深下跌坎水平面底壁附近流速分布,可见:①水流水平流速在落点处分别向两侧分流,并迅速增大至相应最大流速。总体上看,反向水流流速小于主流方向水流流速;②反向水流流速迅速增大至最大流速,之后逐渐减小,至跌坎底部时,水流流速很小,整体上呈“单峰”型式。图 12(b)为相同漫顶水深不同跌坎高度下跌坎水平面底壁流速分布,从中可以看出:①冲射水流依然自水流落点处进行分界,形成流向截然相反的两股水流;②跌坎高度越大,冲射水流落点距跌坎底部距离越远,水流流速越大;③尽管不同工况下水流流速分布存在一定差别,然而在跌坎底部流速均较小,甚至接近于0,这与剪切应力分布规律相类似,表明溃决水流对跌坎根部的直接冲刷作用相对较弱。
|
图 12 不同工况跌坎水平面底壁流速分布 Figure 12 Velocity distribution of horizontal plane near bottom |
漫顶水流作为坝体冲蚀的主导作用力,对于土坝溃决发生、发展过程至关重要,本文采用RNG k-ε紊流模型和VOF技术针对黏性土坝漫顶溃决过程中的代表性水流结构——溃决跌坎水流开展了三维数值模拟研究,揭示了不同工况下坝体跌坎上的剪切应力、流速分布规律,为进一步发展完善黏性土坝漫顶溃决“跌坎式”溯源冲蚀机理提供了理论基础。研究结果表明:
(1) 跌坎冲射水流在落点上游侧并非充满水,而是形成一定深度的坎下回流区,回流区内存在漩涡紊动水流结构;相同坎高工况冲射水平距离和回流区深度均随漫顶水深的增大而增加,不同坎高工况冲射水流结构基本一致,具有较大相似性。
(2) 坝面剪切应力在坝顶上游坝肩位置存在略减小趋势,之后沿程迅速增大,并且在坝顶下缘的坝肩处存在剪切应力极大值;在跌坎水平面水流落点两侧会出现“双峰”分布特征,且下游侧峰值较大;在跌坎水平面与下游坝坡连接部位会出现剪切应力的极大值,而坎后坡面剪切应力沿程逐渐增大,在坝趾处则受体型变化影响出现极小值。
(3) 跌坎垂直面上,剪切应力呈“单峰”分布,在水深中部剪切应力较大,底部及水域上部剪切应力较小;随漫顶水深的增大,剪切应力峰值逐渐增大,最大剪切应力作用点位置也逐渐上移;随跌坎高度逐渐增大,剪切应力峰值存在先增大后减小的趋势。
(4) 跌坎水平面底壁流速在落点处向两侧分流,并迅速增大至相应最大流速。总体上看,反向水流流速呈“单峰”型式,小于主流方向水流流速,至跌坎底部时,水流流速很小;跌坎高度越大,冲射水流落点距跌坎底部距离越远,水平面底壁附近水流最大流速也越大。
(5) 由数模结果分析可知,跌坎水平面上最大水流剪切应力比垂直面上剪切应力要大很多,甚至可达几十倍,由此可初步推断黏性土坝漫顶溃决过程中各级跌坎主要以“台阶水平面刷深下切”的方式进行合并。
| [1] |
中华人民共和国水利部, 中华人民共和国国家统计局. 第一次全国水利普查公报[M]. 北京: 中国水利水电出版社, 2013. ( The Ministry of Water Resources of the People's Republic of China, National Bureau of Statistics of the People's Republic of China. Bulletin of first national census for water[M]. Beijing: China Water Power Press, 2013. (in Chinese))
|
| [2] |
李云, 李君. 溃坝模型试验研究综述[J]. 水科学进展, 2009, 20(2): 304-310. ( LI Yun, LI Jun. Review of experimental study on dam-break[J]. Advances in Water Science, 2009, 20(2): 304-310. (in Chinese)) |
| [3] |
朱勇辉, VISSERP J, VRIJLINGJ K, 等. 堤坝溃决试验研究[J]. 中国科学:技术科学, 2011, 41(2): 150-157. ( ZHU Yonghui, VISSER P J, VRIJLING J K, et al. Experimental investigation on breaching of embankments[J]. Scientia Sinica (Technological), 2011, 41(2): 150-157. (in Chinese)) |
| [4] |
郭军. 欧美国家近期溃坝研究及发展动向[J]. 中国水利, 2005(4): 23-26, 29. ( GUO Jun. Recent studies and activities on dam breach in European countries and United States[J]. China Water Resources, 2005(4): 23-26, 29. (in Chinese)) |
| [5] |
HANSON G J, COOK K R, HUNT S L. Physical modeling of overtopping erosion and breach formation of cohesive embankments[J]. Transactions of the ASAE, 2005, 48(5): 1783-1794. DOI:10.13031/2013.20012 |
| [6] |
ZHANG Jianyun, LI Yun, XUAN Guoxiang, et al. Overtopping breaching of cohesive homogeneous earth dam with different cohesive strength[J]. Science in China Series E: Technological Sciences, 2009, 52(10): 3024-3029. DOI:10.1007/s11431-009-0275-1 |
| [7] |
POWLEDGE G R, RALSTON D C, MILLER P, et al. Mechanics of overflow erosion on embankments[J]. Journal of Hydraulic Engineering, 1989, 115(8): 1056-1075. DOI:10.1061/(ASCE)0733-9429(1989)115:8(1056) |
| [8] |
李云, 王晓刚, 刘火箭, 等. 土石坝漫顶过程水力特性分析[J]. 水动力学研究与进展(A辑), 2012, 27(2): 147-153. ( LI Yun, WANG Xiaogang, LIU Huojian, et al. Overtopping hydraulic characteristics of earth-rock dam[J]. Chinese Journal of Hydrodynamics, 2012, 27(2): 147-153. (in Chinese)) |
| [9] |
魏文礼, 郭永涛, 王纪森. 一维溃坝洪水波的高精度数值模拟[J]. 计算力学学报, 2007, 24(3): 362-364. ( WEI Wenli, GUO Yongtao, WANG Jisen. One-dimensional dam-break numerical simulation based on ENO scheme[J]. Chinese Journal of Computational Mechanics, 2007, 24(3): 362-364. (in Chinese)) |
| [10] |
黄金池, 何晓燕. 溃坝洪水的统一二维数学模型[J]. 水利学报, 2006, 37(2): 222-226. ( HUANG Jinchi, HE Xiaoyan. Unified 2-D numerical model for simulating dam break wave propagation[J]. Journal of Hydraulic Engineering, 2006, 37(2): 222-226. (in Chinese)) |
| [11] |
张新华, 隆文非, 谢和平, 等. 任意多边形网格2D FVM模型及其在城市洪水淹没中的应用[J]. 四川大学学报(工程科学版), 2007, 39(4): 6-11. ( ZHANG Xinhua, LONG Wenfei, XIE Heping, et al. 2D FVM model based on an arbitrary polygonal mesh system for the simulation of flood inundation and its application in municipal regions[J]. Journal of Sichuan University(Engineering Science Edition), 2007, 39(4): 6-11. (in Chinese)) |
| [12] |
夏军强, 王光谦, LINBinliang, 等. 复杂边界及实际地形上溃坝洪水流动过程模拟[J]. 水科学进展, 2010, 21(3): 289-298. ( XIA Junqiang, WANG Guangqian, LIN Binliang, et al. Two-dimensional modelling of dam-break floods over actual terrain with complex geometries using a finite volume method[J]. Advances in Water Science, 2010, 21(3): 289-298. (in Chinese)) |
| [13] |
祝龙, 李云, 宣国祥, 等. 溃坝典型水流水力特性试验研究[J]. 水资源与水工程学报, 2015, 26(5): 132-136. ( ZHU Long, LI Yun, XUAN Guoxiang, et al. Experiment on hydraulic characteristics of typical dam break flow[J]. Journal of Water Resources and Water Engineering, 2015, 26(5): 132-136. (in Chinese)) |
 2017
2017 
