2. 南京水利科学研究院,江苏南京 210029
堆石料由于强度高,变形小,对基础具有很好的适应性,如今已成为土石坝的主要筑坝材料。随着我国经济的快速发展,高土石坝工程在中国西部水电开发中将发挥越来越重要的作用。目前土石坝设计坝高正在从200 m级到300 m级跨越,堆石料的应力应变关系己成为土石坝工程设计和数值计算中的技术挑战之一。对堆石料应力应变规律的研究主要通过常规大三轴试验,其应力路径与堆石料在坝体施工和蓄水过程中的实际应力路径有所不同。已有试验也表明,堆石料的变形特性在坝体填筑和蓄水期都具有明显的应力路径相关性[1-3]。三板溪现场土压力计实测结果表明,在填筑过程中坝体大部分单元都接近等应力比的应力路径[4]。因此检验堆石料本构模型对应力路径的适应性十分必要。对于土石坝工程而言,目前常用的本构模型有邓肯E-B模型[5]、清华KG模型[6]和南水模型[7]。其中邓肯E-B模型为非线性弹性模型,参数较少,物理意义明确,简单实用,能恰当地反映应力水平和围压对剪切变形的影响,但因其依据是广义虎克定律,因此此类模型不能反映材料的剪胀剪缩特性,也不能很好地适应不同的应力路径;清华非线性解耦KG模型建立在大量常规以及特别设定应力路径的大三轴基础上,能够适应多种复杂应力路径;南水模型在理论上较为严密,不再采用以往的弹塑性模型以屈服面为塑性应变等值面的基本假定,对复杂应力路径同样具有一定的适应性。
广义塑性模型最早由Zienkiewicz和Pastor等提出[8-9],在模型中给出显式的塑性流动方向和加载方向以及塑性模量公式,模型理论完善,并且简洁有效。在应用于堆石料的广义塑性模型方面,除了邹德高等提出的广义塑性模型[10]以外,典型的模型还有朱晟等的统一广义塑性模型[11]和陈生水等的考虑颗粒破碎的广义塑性模型[12],三类模型在塑性模量构建上有所不同, 均在堆石料应力应变预测中广泛应用。
目前只有邹德高等[10]和Wei等[13]验证了广义塑性模型对堆石料不同应力路径的适应性,但是二者所针对的试验有差异,同时缺少一定的对比分析。王占军等[14]使用考虑颗粒破碎的广义塑性模型预测了宜兴抽水蓄能电站筑坝堆石料3种应力路径试验,但是仅验证了1组等应力比试验,并且验证的等应力比试验中R=dσ1/dσ3=8,对应等应力比R很大,接近三轴加载(R=+∞)情况,这其实不利于发现此类模型对应力路径的适应性规律。总的来说,目前对广义塑性模型应力路径适应性的研究尚不充分,没有针对同一系列试验进行广义塑性模型与其他模型预测效果的对比研究。
为了更好地阐释广义塑性模型对应力路径适应性规律,本文首先在文献[15]基础上提出一个修正的广义塑性模型,同时考虑到南水模型理论严密合理,对应力路径有一定的适应性,进行广义塑性模型与南水模型的多种应力路径适应性对比研究,以此分析和揭示广义塑性模型对多种应力路径适应性规律。本文选择的验证试验为杨光等开展的具有丰富数据的某花岗岩堆石料多种应力路径试验[16]。考虑沈珠江院士提出的南水模型采用抛物线型体变曲线会明显高估堆石料的峰后体胀,在预测堆石料剪胀(缩)方面有一定的不足,本文选择王庭博等提出的改进的南水模型[17]作为与广义塑性模型预测对比的另一类弹塑性模型。
1 二类模型及常规三轴试验验证 1.1 修正的广义塑性模型文献[15]针对砂土类广义塑性模型对堆石料应力应变预测效果较差的问题,引入塑性功,提出了一个修正的广义塑性模型,较好地模拟了堆石料三轴加载过程。由于引入塑性功修正,使得参数难以确定,并且在水工结构计算中需不断更新塑性功,计算效率较低,为了克服这一缺陷,本文在文献[15]基础上提出另一类修正广义塑性模型,此类模型不再引入塑性功修正塑性模量,并且对于三轴加载试验可以达到与文献[15]相同的预测效果,本文验证和分析此类模型对多种应力路径的适应性,并与修正的南水模型进行对比。
修正的广义塑性模型中除了塑性模量以及峰值强度公式以外,其他与文献[15]相同。修正广义塑性模型中塑性模量采用如下表达式:
| $ H=H_{0P_\text{a}}(9/p_\text{a})^mH_1H_2 $ | (1) |
式中:H0为模型参数;pa为大气压力;m为材料属性参数,一般在0到1之间,H1和H2表达式如下:
| $ {H_1} = 1 - {(\eta /{M_{\rm{f}}})^\beta } $ | (2) |
| $ {H_2} = \exp (\gamma \eta /{M_{\rm{f}}}) $ | (3) |
式中:H1和H2分别为针对文献[14]中提到的高围压下三轴加载初始阶段塑性模量偏大和加载后期偏小而引入的两个修正系数;β,γ均为模型参数,根据具体堆石料试验不同围压下的q-εa曲线确定。由于修正系数H1小于原始砂土广义塑性模型中1-η/Mf项,修正系数H2始终大于1,而且在后期尤为明显,引入这两个修正系数可以很好地增强模型对高围压的适应性。
考虑三轴加载试验中平均压力对峰值强度的影响[18],其中Mf采用如下表达式:
| $ {M_{\rm{f}}} = M{(p/{p_{\rm{c}}})^{ - n}} $ | (4) |
式中:Mf为剪胀应力比;pc为破碎参考应力;在确定pc以后,M,n由不同围压下峰值强度拟合得到。
1.2 修正的南水模型王庭博等[17]通过修正南水模型切线模量和切线体积比,改进了南水模型在剪胀(缩)特性方面和模型中破坏比参数的运用使试样始终处于硬化状态的不足,更好地模拟了堆石料的强度和变形特性。
南水模型由以下两类屈服面组成:
| $ f_1=p^2+r^2q^2 $ | (5) |
| $ f_2=q^s/p $ | (6) |
式中:r和s为模型的两个参数,对于堆石料一般取2。
采用正交流动法则,应力应变增量关系表示成如下形式:
| $ \Delta \varepsilon = {D^{ - 1}}\Delta \sigma + {A_1}\frac{{\partial {f_1}}}{{\partial \sigma }}\Delta {f_1} + {A_2}\frac{{\partial {f_2}}}{{\partial \sigma }}\Delta {f_2} $ | (7) |
式中:D-1为弹性柔度矩阵;A1和A2为塑性系数。
在修正的南水模型中:
| $ {E_{\rm{t}}} = {(1 - \eta /{M_{\rm{f}}})^\alpha }K{p_{\rm{a}}}{({\sigma _3}/{p_{\rm{a}}})^n} $ | (8) |
| $ {\mu _{\rm{t}}} = {\mu _{{\rm{t0}}}}[1-{(\eta /{M_{\rm{f}}})^4}] $ | (9) |
式中:K为初始弹性模量系数;n为弹性模量随围压变化的幂次;σ3为围压;η为应力比;α和μt0为模型参数;Mf为峰值应力比;Mc为剪胀应力比。Mf和Mc的具体表达式如下:
| $ {M_{\rm{f}}} = 6\sin {\varphi _f}/3 - \sin {\varphi _f}, {\varphi _{\rm{f}}} = {\varphi _0} - \log ({\sigma _3}/{p_{\rm{a}}})\Delta \varphi $ | (10) |
| $ {M_{\rm{c}}} = 6\sin {\psi _{\rm{c}}}/3 - \sin {\psi _c}, {\psi _{\rm{c}}} = {\psi _0} - \log ({\sigma _3}/{p_{\rm{a}}})\Delta \psi $ | (11) |
式中:φf为峰值摩擦角;φ0为围压大气压时对应的峰值摩擦角;Δφ为围压增加1个数量级峰值摩擦角降低的幅度;ψc为临胀摩擦角;ψ0为围压大气压时对应的剪胀摩擦角;Δψ为围压增加1个数量级剪胀摩擦角降低的幅度。
根据常规三轴加载试验条件,以及Et和μt的定义可以解出A1和A2,假定三轴状态下的塑性系数A1和A2可以直接用于其他应力状态,根据π平面上采用Prandtl-Reuss流动法则将式(7) 式解成6个方向应变进而可求得弹塑性矩阵。
1.3 三轴试验验证对于修正的广义塑性模型,根据清华大学杨光等[16]的试验数据,整理弱风化花岗岩(v=0.3) 常规三轴加载试验资料可得参数α=0.4,Mg=1.652,M=1.547,n=0.11,G0=540,pc=3 800 kPa,由于缺少等向压缩试验资料,对应参数β,γ,m,H0通过拟合三轴试验应力应变曲线,采用IGA反演确定[19],具体为β=0.19, ν=2.0, m=0.74, H0=8 460。
对于修正的南水模型,所有参数均可通过整理三轴试验数据得到,其中参数α和μt0通过整理不同围压下Et-η/Mf和dεv/dε1-η/Mc曲线得到。由于缺少卸载试验数据,模型中的卸载弹性模量系数Kur参考文献[20]研究成果,近似取K值的2倍。对于该弱风化花岗岩,修正南水模型所用参数取值为φ0=49.4°,Δφ=9.0°,ψ0=47.2°,Δψ=7.1°,K=710,Kur=1 420,n=0.25,α=0.8,μt0=0.95。
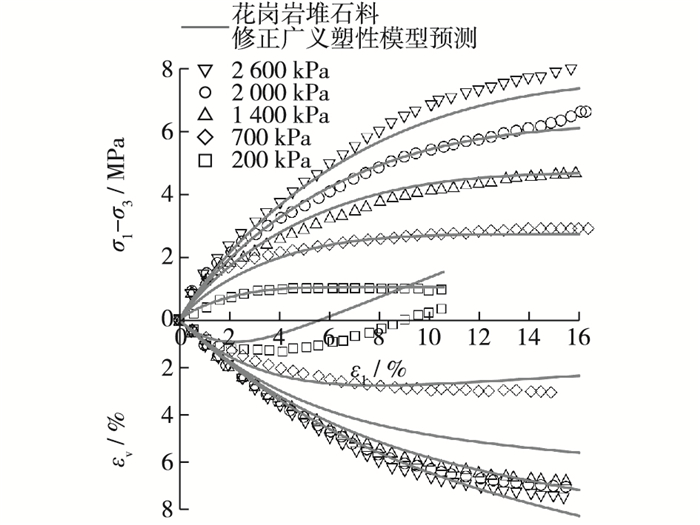
对于这二类模型,在实际Fortran程序实现的时候, 若η>Mf,取η=0.99Mf,以保证程序可以顺利执行。两类模型预测的三轴试验结果分别见图 1和2,从模拟结果可以看出提出的广义塑性模型和修正的南水模型均可较好地模拟堆石料三轴加载应力应变规律,与南水模型相比,本文提出的广义塑性模型同样对常规三轴加载应力路径具有很好的适应性。
|
图 1 修正广义塑性模型三轴试验预测结果 Figure 1 Comparison between experimental results and modified P-Z model predictions |

|
图 2 南水模型三轴试验预测结果 Figure 2 Comparison between test results and NHRI model predictions |
在通过常规三轴试验确定上述两类模型的参数以后,本文通过Fortran程序,使用常规三轴试验确定的参数分别验证两类模型对文献[15]中4组围压下等p试验(平均应力p恒定,偏应力q不断增加至破坏)以及4种应力比下的等应力比加载试验的预测效果。
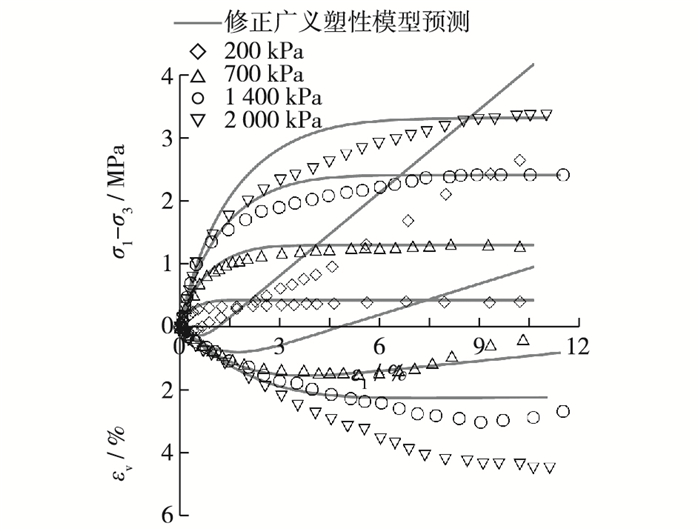
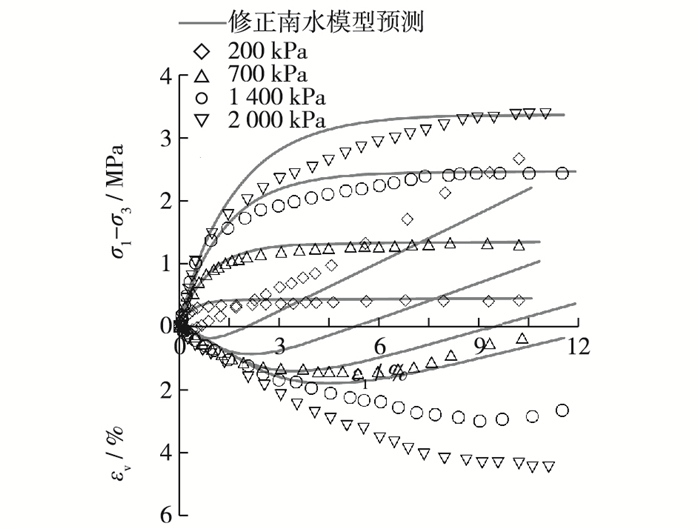
2.1 等p试验预测对比使用1.3节方法确定的两类模型参数分别预测了4种围压条件下的等p加载试验,预测结果如图 3和4。对于堆石料三轴等p加载试验,由于在剪应力增加的过程中,围压在不断减小,使得试样受到的侧向约束也不断减小,有利于剪胀的发生,这样剪缩体变将明显小于相同固结围压下的常规三轴试验。从图 3和4可以看出,两类模型均可以很好地预测堆石料的强度特性,并且预测得到的体变也是小于相应常规三轴加载下的剪缩体变,符合等p试验基本规律。但是两类模型预测的体变与试验值相比,偏小很多。对于修正广义塑性模型,这间接说明了相同围压下等p试验剪胀规律与常规三轴试验有所不同,由常规三轴试验得到的剪胀参数直接应用于等p试验会产生一定偏差;对于南水模型,预测体应变偏小的原因在于由常规三轴试验得到的塑性系数A1和A2可能不适合等p试验,造成预测的等p试验体变偏差较大。
|
图 3 修正广义塑性等p试验预测结果 Figure 3 Comparison constant p test results and modified P-Z model predictions |
|
图 4 南水模型等p试验预测结果 Figure 4 Comparison between constant p test results and NHRI model predictions |
总体而言,广义塑性模型与南水模型对等p加载应力路径具有相似的适应性,均可以较好地预测堆石料等p试验强度特性,但是若采用三轴试验剪胀参数,两类模型可能会低估等p试验下堆石料的体缩特性,预测出较小的体缩变形,两类模型并不能较好地反映轴向加载和径向卸载同时作用下的应变响应情况。
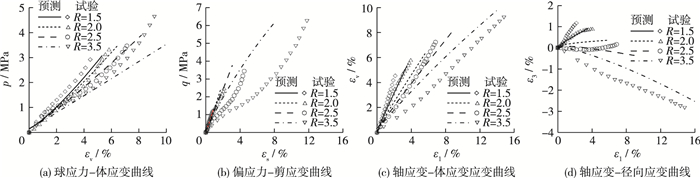
2.2 等应力比试验预测结果对于实际筑坝的堆石料,等应力比路径是一类值得重视的应力路径。对于前文所述两类模型,本文使用1.3节确定的参数同样预测了4组等应力比试验,对应4组等应力比R=dσ1/dσ3=1.5,2.0,2.5,3.5,分别预测了球应力-体积应变关系曲线、剪应力-剪应变关系曲线、体积应变-轴向应变关系曲线、径向应变-轴向应变关系曲线。图 5和6分别为修正广义塑性模型和修正南水模型等应力比试验预测结果,从总体预测结果来看,修正南水模型的预测好于广义塑性模型,南水模型可反映等应力加载下的堆石料应力应变规律。对于广义塑性模型,若采用常规三轴条件下的剪胀方程,剪应力-剪应变和径向应变-轴向应变的预测均与实际试验有一定的偏差。同时广义塑性模型对高等应力比试验适应性明显强于低应力比试验,可以大体反映高等应力比试验基本规律。

|
图 5 修正广义塑性模型等应力比试验预测结果 Figure 5 Comparison between constant stress ratio tests results and P-Z model predictions |
|
图 6 修正南水模型等应力比试验预测结果 Figure 6 Comparison between constant stress ratio tests results and NHRI model predictions |
从图 5(d)和图 6(d)对比可见,广义塑性模型在径向应变预测方面不及修正南水模型准确,广义塑性模型很难预测出较大的径向收缩应变,随着等应力比的增大,三轴试验径向变形很快从径向收缩转变为径向膨胀,使用朱晟等的统一广义塑性模型[11]和陈生水等的考虑颗粒破碎的广义塑性模型[12]以及Wei等的广义塑性模型[13]同样存在这个问题。这主要有两个原因:第一,在使用Fortran程序预测等应力比试验应变的时候,主要是应力控制,给定应力增量通过柔度矩阵求得应变增量,逐步累加应变,由于等应力比试验中轴向和径向同时加载,实际试验中的剪胀(缩)规律与常规三轴试验有一定差异,而预测的过程中仍然采用了三轴加载下的剪胀方程,这样低估等应力比试验下的堆石料的剪缩性,因此根据相同应力条件下预测的体变偏小,剪应变偏大,根据ε3=(2εv-3εs)/6,则预测的径向应变偏小很多;第二,广义塑性模型中若干参数不是根据具体等向压缩试验确定,而是通过优化算法反演得到,主要是基于三轴加载情况反演,带有一定人为性,在反演参数较多的情况下,反映的是多个参数综合影响特性,也会产生一定误差。这些原因导致了广义塑性模型预测径向应变的结果不理想,等应力比加载下的剪胀方程需要改进。
而南水模型则不同,放弃了弹塑性模型以屈服面为塑性应变等值面的基本假定,把屈服面只看作弹性区的界面,模型的建立基于等价应力理论,假定三轴状态下测定的塑性系数可用于其他应力状态,根据常规三轴试验的应力条件,可通过切线弹性模量Et、切线体积泊松比μt来确定反映硬化的塑性系数A1和A2,而塑性系数A1和A2又可用于其他应力路径,由于切线弹性模量Et和切线体积泊松比μt可以较为准确地确定,这样对应力应变的预测相对准确很多,对等应力比试验径向体变预测也更接近试验值。图 6(b)出现偏差的原因在于径向应变与轴向应变虽与试验值较为接近,但是仍存在一定偏差,其累计效应正好造成了剪应变的偏差较大,这一点与广义塑性模型预测出现偏差原因不同。
2.3 等应力比试验剪胀方程改进根据文献[15],在广义塑性模型框架下,剪胀方程往往采用如下表达式:
| $ {d_{\rm{g}}} = \frac{{{\rm{d}}\varepsilon _{\rm{v}}^p}}{{{\rm{d}}\varepsilon _{\rm{s}}^p}} = (1 + \alpha )({M_{\rm{g}}} - \eta ) $ | (12) |
式中:α和Mg为剪胀参数。
对于等应力比试验,η=3(R-1)/(R+2),等应力比R=dσ1/dσ3=1.5,2.0,2.5,3.5对应的应力比η分别为0.429,0.75,1.0,1.364,将α和Mg以及η代入剪胀方程(12),可得dg分别为1.712,1.263,0.918,0.403;另一方面,根据花岗岩堆石料等应力比试验数据[19],假定
考虑等应力比试验剪胀(缩)规律与常规三轴试验的差异与联系,分析等应力比试验数据,本文给出如下形式统一考虑常规加载与等应力比加载的剪胀方程。
| $ \frac{{{\rm{d}}\varepsilon _{\rm{v}}^p}}{{{\rm{d}}\varepsilon _{\rm{s}}^p}} = \delta (R)(1 + \alpha )({M_{\rm{g}}} - \eta ) $ | (13) |
| $ \delta (R) = \left\{ {\begin{array}{*{20}{c}} {1, R \geqslant 2.6} \\ {{k_1}/R - {k_2}, 1 \leqslant R < 2.6} \end{array}} \right. $ | (14) |
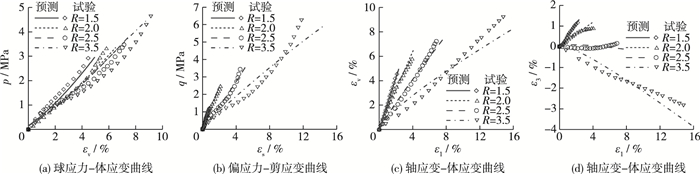
式中:R=dσ1/dσ3,δ(R)为修正系数;α,Mg的意义及取值同1.1节修正广义塑性模型,k1,k2为等应力比试验剪胀参数,针对本文花岗岩堆石料试验,k1=13.52,k2=4.09。常规三轴条件下dσ3=0,R→+∞,修正系数δ(R)等于1,剪胀方程退化为常规三轴试验剪胀方程。采用式(13) 定义的修正系数,表明当R≥2.6时,等应力比试验剪胀方程与常规三轴试验一致,不考虑二者剪胀规律的差异性,而文献[10-14]均采用与常规三轴试验相同的剪胀方程。采用修正剪胀方程的模型预测的等应力比试验结果见图 7,通过与图 5对比可知,采用修正的剪胀方程以后,广义塑性模型对等应力比路径试验预测精度明显提高,可以很好地预测堆石料等应力比加载试验。
|
图 7 改进剪胀方程应力比试验预测结果 Figure 7 Comparison between improved model predictions and constant stress vatio tests results |
(1) 提出了1个修正的广义塑性模型,对不同应力路径堆石料试验,进行了广义塑性模型模型与南水模型的应力路径适应性对比研究,预测结果表明:广义塑性模型对常规加载应力路径具有很好的适应性,广义塑性模型与南水模型可以合理地反映等p加载试验强度特性,但是对体变预测相对偏小,两类模型均低估了等p试验下堆石料的体缩特性。
(2) 南水模型对等应力比试验的预测结果优于广义塑性模型,广义塑性模型对等应力比试验应力应变预测结果与实际偏差较大,其主要原因在于常规三轴试验下的广义塑性模型剪胀方程并不适用等应力比试验。
(3) 推导了适用于常规三轴和等应力比试验的修正剪胀方程,在广义塑性模型框架下,使用修正的剪胀方程可以明显提高堆石料等应力比试验预测精度。
(4) 本文仅预测了3种不同应力路径加载下堆石料的应力应变特性,对于实际的堆石料在蓄水期还会发生应力路径转折,模型对于复杂的转折应力路径的适应性仍需进一步研究。
| [1] |
刘祖德. 土石坝变形计算的若干问题[J]. 岩土工程学报, 1983, 5(1): 1-13. ( LIU Zude. Some problems about the calculation of deformation of earth-rock dams[J]. Chinese Journal of Geotechnical Engineering, 1983, 5(1): 1-13. (in Chinese)) |
| [2] |
柏树田, 周晓光, 晁华怡. 应力路径对堆石变形特性的影响[J]. 水力发电学报, 1999(4): 76-80. ( BAI Shutian, ZHOU Xiaoguang, CHAO Huayi. Effects of stress path on the deformation of rockfill materials[J]. Journal of Hydroelectric Engineering, 1999(4): 76-80. (in Chinese)) |
| [3] |
谢婉丽. 大坝应力路径条件下粗粒料的强度和变形特性的研究[D]. 昆明: 昆明理工大学, 2001. (XIE Wanli. The analysis of the specific property of the coarse materials strength and deformation under dam stress paths[D]. Kunming: Kunming University of Science and Technology, 2001. (in Chinese))
|
| [4] |
南瑞集团公司. 清水江三板溪水电站大坝及泄水建筑物安全监测系统大坝及泄水建筑物安全监测系统年终总结分析报告[R]. 南京: 南瑞集团公司, 2008. (Nanri Group Corporation. Year-end monitoring system summary and analysis report of Sanbanxihydropower dam and discharge structure[R]. Nanjing: Nanri Group Corporation, 2008. (in Chinese))
|
| [5] |
DUNCAN J M, CHANG C Y. Nonlinear analysis of stress and strain in soils[J]. Soil Mechanics and Foundation Division Journal, 1970, 96(5): 1629-1653. |
| [6] |
高莲士, 汪召华, 宋文晶. 非线性解耦K-G模型在高面板堆石坝应力变形分析中的应用[J]. 水利学报, 2001, 32(10): 1-7. ( GAO Lianshi, WANG Zhaohua, SONG Wenjing. The application of nonlinear uncoupled K-G model to deformation analysis of high concrete face rockfill dam[J]. Journal of Hydraulic Engineering, 2001, 32(10): 1-7. DOI:10.3321/j.issn:0559-9350.2001.10.001 (in Chinese)) |
| [7] |
沈珠江. 理论土力学[M]. 北京: 中国水利水电出版社, 2000: 53-54. ( SHEN Zhujiang. Theoretical soil mechanics[M]. Beijing: China Water Power Press, 2000: 53-54. (in Chinese))
|
| [8] |
ZIENKIEWICZ O C, MROZ Z. Generalized plasticity formulation and applications to geomechanics[C]//Mechanics of Engineering Materials. New York: Wiley, 1984: 655-679.
|
| [9] |
PASTOR M, ZIENKIEWICZ O C, CHAN A H C. Generalized plasticity and the modeling of soil behavior[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1990, 14: 151-190. DOI:10.1002/(ISSN)1096-9853 |
| [10] |
邹德高, 付猛, 刘京茂, 等. 粗粒料广义塑性模型对不同应力路径适应性研究[J]. 大连理工大学学报, 2013, 53(5): 702-709. ( ZOU Degao, FU Meng, LIU Jingmao, et al. Study of adaptability of generalized plastic model of coarse grained soil under various stress paths[J]. Journal of Dalian University of Technology, 2013, 53(5): 702-709. DOI:10.7511/dllgxb201305014 (in Chinese)) |
| [11] |
朱晟, 魏匡民, 林道通. 筑坝土石料的统一广义塑性本构模型[J]. 岩土工程学报, 2014, 36(8): 1394-1399. ( ZHU Sheng, WEI Kuangmin, LIN Daotong. Generalized plasticity model for soil and coarse-grained dam materials[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(8): 1394-1399. DOI:10.11779/CJGE201408003 (in Chinese)) |
| [12] |
陈生水, 傅中志, 韩华强, 等. 一个考虑颗粒破碎的堆石料弹塑性本构模型[J]. 岩土工程学报, 2011, 33(10): 1489-1495. ( CHEN Shengshui, FU Zhongzhi, HAN Huaqiang, et al. An elastoplastic model for rockfill materials considering particle breakage[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(10): 1489-1495. (in Chinese)) |
| [13] |
WEI Kuangmin, ZHU Sheng. A generalized plasticity model to predict behaviors of the concrete-faced rock-fill dam under complex loading conditions[J]. European Journal of Environmental and Civil Engineering, 2013, 17(7): 579-597. DOI:10.1080/19648189.2013.805166 |
| [14] |
王占军, 陈生水, 傅中志. 堆石料的剪胀特性与广义塑性本构模型[J]. 岩土力学, 2015, 36(7): 1931-1938. ( WANG Zhanjun, CHEN Shengshui, FU Zhongzhi. Dilatancy behaviors and generalized plasticity constitutive model of rockfill materials[J]. Rock and Soil Mechanics, 2015, 36(7): 1931-1938. (in Chinese)) |
| [15] |
卞士海, 李国英, 魏匡民, 等. 堆石料广义塑性模型研究[J]. 岩土工程学报, 2017, 39(6): 996-1003. ( BIAN Shihai, LI Guoying, WEI Kuangmin, et al. Study on generalized plasticity model of rockfill materials[J]. Chinese Journal of Geotechnical Engineering, 2017, 39(6): 996-1003. (in Chinese)) |
| [16] |
杨光, 孙逊, 于玉贞, 等. 不同应力路径下粗粒料力学特性试验研究[J]. 岩土力学, 2010, 31(4): 1118-1122. ( YANG Guang, SUN Xun, YU Yuzhen, et al. Experimental study of mechanical behavior of a coarse-grained material under various stress paths[J]. Rock and Soil Mechanics, 2010, 31(4): 1118-1122. (in Chinese)) |
| [17] |
王庭博, 陈生水, 傅中志. "南水"双屈服面模型的两点修正[J]. 同济大学学报(自然科学版), 2016, 44(3): 362-368. ( WANG Tingbo, CHEN Shengshui, FU Zhongzhi. Two modifications to the Shen Zhujiang's double yield surface model[J]. Journal of Tongji University(Natural Science), 2016, 44(3): 362-368. (in Chinese)) |
| [18] |
王乃东, 姚仰平. 粒状材料颗粒破碎的力学特性描述[J]. 工业建筑, 2008, 38(8): 17-20. ( WANG Naidong, YAO Yangping. Mechanicaldescription for granular material exhibiting particle crushing[J]. Industrial Construction, 2008, 38(8): 17-20. (in Chinese)) |
| [19] |
朱晟, 王永明, 胡祥群. 免疫遗传算法在土石坝筑坝粗粒料本构模型参数反演中的应用研究[J]. 岩土力学, 2010, 31(3): 961-966. ( ZHU Sheng, WANG Yongming, HU Xiangqun. Application of immune genetic algorithm to back analysis for parameters in model of rockfill dam coarse grain materials[J]. Rock and Soil Mechanics, 2010, 31(3): 961-966. (in Chinese)) |
| [20] |
FU Zhongzhi, CHEN Shengshui, PENG Cheng. Modeling cyclic behavior of rockfill materials in a framework of generalized plasticity[J]. International Journal of Geomechanics, 2015, 14(2): 191-204. |
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2017
2017 