2. 三峡大学土木与建筑学院, 湖北宜昌 443002
大坝、海洋平台及桥墩等建筑物常常受外界水压力和荷载历史等因素的影响,导致整个结构的功能丧失,甚至破坏。目前,对混凝土力学性能的研究多数仅考虑单一因素的影响,而当混凝土遭受多因素相互作用时,对其力学性能的研究还相对较少。
Butler[1]研究发现,水环境中主动孔隙水压力使材料产生的拉应变是造成混凝土开裂的主要原因。Xuan等[2]进行了高围压下混凝土抗压性能试验,结果表明高围压下混凝土内的孔隙水对混凝土强度有较大削弱。CHEN Z等[3]选择混凝土内水分含量、荷载作用方式以及加载速率等影响因素,对混凝土的多轴强度进行了研究。彭刚等[4]进行了有压孔隙水环境中不同加载速率下混凝土抗压性能试验,发现在有压水环境中,混凝土峰值应力随围压的提升而增大,增大幅度随加载速率加快而升高,混凝土率敏感性由于围压的影响而提高。Bruhwiller等[5]研究了经历多次预压荷载作用后混凝土断裂特性的改变。林皋等[6]通过楔入劈拉试验研究了历经荷载循环后混凝土的断裂特性,发现混凝土的断裂特性是受加载历史影响的物理量;随后研究了三向等压荷载历史对混凝土强度的影响,给出了混凝土强度与荷载历史关系的经验表达式[7]。肖诗云等[8]对历经极限抗压强度荷载作用后的混凝土试件,进行不同加载速率下的动态抗压试验,研究了不同加载速率下荷载历史对混凝土应力应变空间损伤演化规律的影响。
综上所述,围压、循环荷载和加载速率对混凝土力学性能有较大影响。基于此,对历经循环荷载作用后不同水围压下混凝土的效应特性进行研究。
1 试验设计试验所用仪器为三峡大学10 MN大型多功能三轴仪。该加载系统可进行10-5/s~10-2/s加载速率范围的静动态加载试验,竖向最大行程为300 mm,可提供最大动态和静态加载压力分别为5和10 MN。水环境加载设备可进行水平和竖向加孔隙水压试验,能提供的最大围压和最大孔隙水压力值均为30 MPa。
试验所用的混凝土试件为Φ150×300 mm圆柱体,设计强度30 MPa,试件成型方式为钢模浇筑,在自然环境下静置24 h成型后拆模并编号,标准养护28 d后置于自然环境中。试件所用水泥为宜昌三峡水泥有限公司生产的P·O 42.5硅酸盐水泥;水为自来水;粗骨料采用5~30 mm连续级配河卵石;细骨料为连续级配天然河砂,细度模数为1.8,属细砂。拌合物坍落度为5~30 mm,满足和易性要求。混凝土材料用量为:粗骨料1 171.8 kg/m3,细骨料718.2 kg/m3,水170.0 kg/m3,水泥340.0 kg/m3。
在进行力学试验前,需要使打磨后的试件处于水饱和状态。处理方法为:在围压桶中加压(围压值与加载时相同)浸泡24 h后,水环境加载系统中驱动器位移不随时间改变,则认为混凝土试件已经满足水饱和状况。
加载试验时首先经过平均值、振幅和频率分别为200 kN,60 kN和0.1 Hz的25次循环荷载作用,循环加载结束后竖向荷载降至20 kN,再用计算机操作三轴系统以试验所需的加载速率进行加载直至试件失去承载能力(见图 1),加载试验过程中保证水环境系统中的水压力不变。

|
图 1 围压2 MPa下加载速率10-5/s~10-2/s时试件的破坏 Figure 1 Failure of test specimen under 2 MPa confining pressures with loading rate from 10-5/s to 10-2/s |
表 1为混凝土在不同围压以及不同加载速率下的峰值应力统计,其变化趋势分别见图 2和图 3。
| 表 1 混凝土峰值应力统计 Table 1 Concrete peak stress statistics |
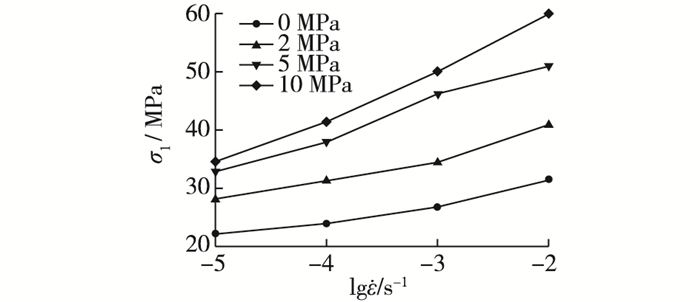
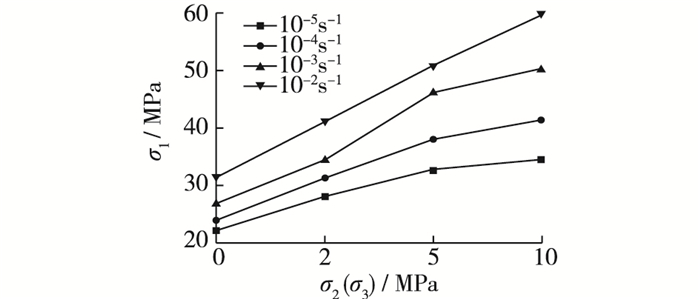
分析表 1和图 2可知,随着加载速率的升高,历经荷载循环后不同围压状况下混凝土材料的峰值应力呈增大趋势。随着加载速率的增加(以10-5/s为静态加载速率),历经循环荷载后不同围压状况下混凝土材料的峰值应力增加幅度逐渐增大。由表 1和图 3可知,水环境状态下围压升高时,历经循环荷载后混凝土峰值应力呈增大趋势。
|
图 2 峰值应力随加载速率的变化 Figure 2 Peak stress changing with loading rates |
|
图 3 峰值应力随围压的变化 Figure 3 Peak stress changing with confining pressures |
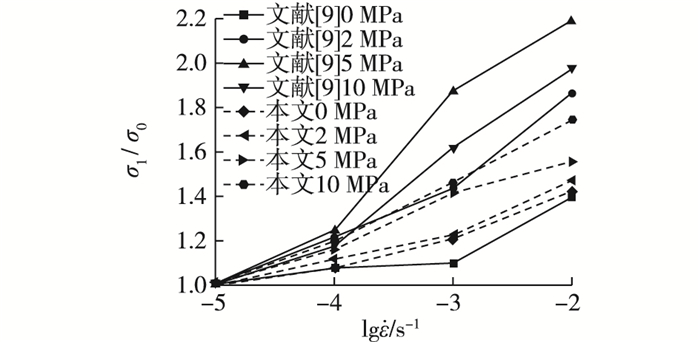
将文献[9]以及试验得到的混凝土在不同加载速率、不同围压下的峰值应力绘于图 4。可见,混凝土抗压峰值应力都随加载速率的增加而增加,水饱和混凝土的峰值应力随围压的增大而增大。在围压为0情况下,历经循环荷载历史的混凝土比未经循环荷载历史的混凝土峰值强度增加幅度高,即率敏感性增强。在围压为2, 5和10 MPa情况下,循环加载历史降低了混凝土率敏感性。分析其原因,混凝土在经历循环荷载时会经历压实过程,随着围压升高会更快地从压密阶段进入弹塑性变形阶段,在围压为0情况下,经过25次循环荷载的混凝土变得更加密实,孔隙间的距离变得更小,Stefan效应增强,因此,围压为0时水饱和混凝土率敏感性提高;围压为2,5,10 MPa情况下,由于存在围压,混凝土经过25次循环荷载后已经从压实阶段进入弹塑性变形阶段,混凝土形成了比较大的贯通裂缝,相应地削弱了Stefan效应,因此2,5,10 MPa围压水饱和混凝土率敏感性相对于未经循环荷载历史的试件要低。
|
图 4 不同加载速率及不同围压下混凝土的峰值应力增幅对比 Figure 4 Comparison of peak stress increase of concrete under different loading rates and different confining pressures |
试验结果表明,随加载速率增加,混凝土动态峰值应力的增幅与加载速率的对数有线性增长变化规律用下式[10]拟合:
| $ {C_{{\text{DIF}}}} = 1 + m\lg ({{\dot \varepsilon }_{\text{c}}}/{{\dot \varepsilon }_{{\text{cs}}}}) $ | (1) |
式中:CDIF为混凝土动态抗压峰值应力增长值,CDIF=σ/fcs;σ为当前加载速率下的峰值应力;fcs为静态加载速率下的峰值应力;
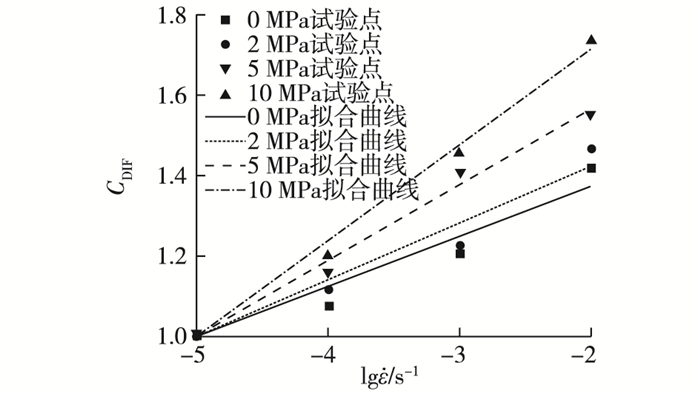
用式(1) 对水饱和混凝土试件的动态强度进行最小二乘法拟合,得到0, 2,10 MPa围压下拟合参数m分别为0.124 17,0.140 52,0.238 02;R2分别为0.935 7,0.952 4,0.991 7,动态强度增幅与加载速率的变化规律见图 5。
|
图 5 峰值应力增加幅度与加载速率的关系 Figure 5 Relationships between amplitude of peak stresses and loading rates |
由图 5可知,随着围压升高,加载速率对历经循环荷载后混凝土材料峰值应力的影响增大,即当水环境状态下围压升高时,历经荷载循环后峰值应力的率敏感性增强。分析原因:随着围压增加,围压阻碍混凝土横向开裂的能力增强,因此强度增大;与此同时混凝土破坏时水会更快地进入到新生成的裂缝中,导致混凝土内部含水量增加,黏性效应增强,因此率敏感性增强。按照莫尔-库仑准则推导出混凝土三轴强度公式[11]。
| $ {\sigma _1} = {f_{\rm{c}}} + k{\sigma _3} $ | (2) |
式中:σ1为轴向峰值应力;fc为混凝土单轴抗压强度;σ3为围压值,k为常数。
将式(2) 进行变换后得如下公式:
| $ {\sigma _1}/{f_{\rm{c}}} = 1 + k{\sigma _3}/{f_{\rm{c}}} $ | (3) |
对表 1中的试验数据用式(3) 进行线性回归分析,结果表明:随着加载速率的增大,拟合参数k与加载速率的对数表现出线性变化规律,用式(4) 拟合:
| $ k = a + b\lg {{\dot \varepsilon }} $ | (4) |
拟合得到参数a和b,变化趋势见图 6。
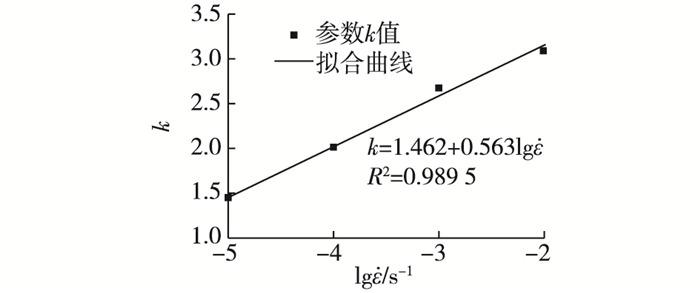
|
图 6 参数k与加载速率的线性拟合 Figure 6 Linear fitting of parameter k and loading rate |
将式(4) 代入式(2),能够得到历经荷载循环后混凝土动态峰值应力与围压、加载速率有关的经验式(5):
| $ {\sigma _1}/{f_{\rm{c}}} = 1 + (a + b\lg {{\dot \varepsilon }}){\sigma _3}/{f_{\rm{c}}} $ | (5) |
不同加载速率下,历经荷载历史循环后水饱和混凝土试件的峰值应变值如表 2所示,变化关系曲线见图 7和8。
| 表 2 混凝土的峰值应变 Table 2 Peak strain of concrete |
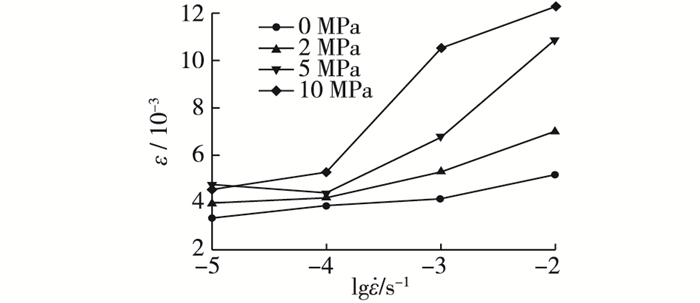
|
图 7 峰值应变随加载速率变化 Figure 7 Peak strain changing with loading rates |
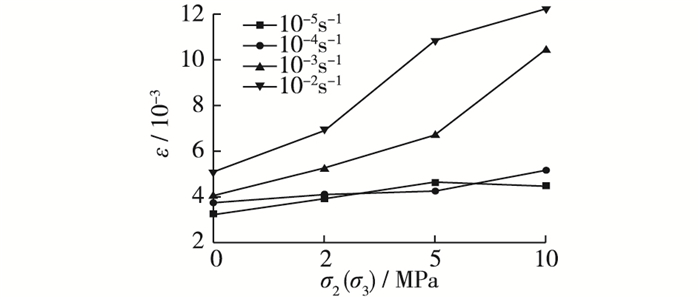
|
图 8 峰值应变随围压变化 Figure 8 Peak strain changing with confining pressures |
分析表 2和图 7得知,随着加载速率的增大,历经荷载循环后混凝土峰值应变整体上呈逐渐增大的趋势。水饱和混凝土试件的峰值应变,在加载速率为10-4/s,10-3/s,10-2/s时相对于加载速率为10-5/s时增加的百分比见表 2。由表 2和图 8得知,随着水环境中围压的升高,混凝土峰值应变有逐渐增大的变化趋势。
对比分析数据,随着加载速率的增加,混凝土动态变形的增幅与加载速率的对数呈线性增长的趋势,用如下公式拟合。
| $ {\varepsilon _{\rm{c}}}/{\varepsilon _{{\rm{cs}}}} = 1 + \mu \lg ({{\dot \varepsilon }_{\rm{c}}}/{{\dot \varepsilon }_{{\rm{cs}}}}) $ | (6) |
式中:εcs为混凝土在加载速率为10-5/s时的峰值应变;εc为混凝土在加载速率为10-4/s,10-3/s,10-2/s时的峰值应变;μ是代表混凝土力学特征的参数。
用式(6) 对水饱和混凝土试件的动态变形进行最小二乘法拟合,得到变化规律见图 9。

|
图 9 峰值应变增加幅度与加载速率的关系 Figure 9 Relationships between amplitude of peak strains and loading rates |
分析图 9可知,随着水围压的增大,峰值应变增量与加载速率对数的拟合曲线的斜率μ逐渐增大,即围压提高了峰值应变的率敏感性。原因分析:围压作用下阻碍了混凝土内的微裂纹不能继续扩展,不能进一步形成宏观裂缝,同时混凝土开裂过程中水进入新开裂的裂缝内部导致整个混凝土试样的黏性效应增加,混凝土发生挤压流动和塑性变形,直至破坏,最终混凝土变形增大,峰值应变的率敏感性提高。对比分析可知,随水围压的增加,拟合参数μ与围压呈线性关系,μ=a+bσ3,拟合效果见图 10。
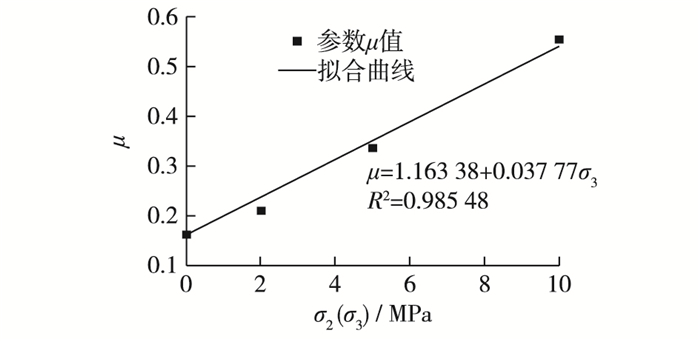
|
图 10 参数μ与围压的拟合 Figure 10 Fitting of parameters μ and confining pressure |
将拟合式μ=a+bσ3代入式(6),得到历经荷载循环后混凝土动态峰值应变与围压、加载速率有关的经验式(7):
| $ {\varepsilon _{\rm{c}}}/{\varepsilon _{{\rm{cs}}}} = 1 + (a + b{\sigma _3})\lg ({{\dot \varepsilon }_{\rm{c}}}/{{\dot \varepsilon }_{{\rm{cs}}}}) $ | (7) |
由于混凝土凝固初期水化热等影响,其成型后内部会存在一定的裂缝和孔隙。当有外部荷载作用在试件上时,内部初始孔隙就会逐渐发展并且整个过程是连续的。不仅如此,裂缝发展的主方向和荷载的施加方向呈一定的角度,并且刚好为90°。到目前为止,较多的研究者已经推导出了不同的混凝土损伤本构模型,而且模型各有差异。基于试验成果,采用Weibull-Lognormal损伤本构模型的混凝土应力-应变关系式。从而,建立起如下所示的损伤模型:
| $ \sigma = \left\{ {\begin{array}{*{20}{c}} {E\varepsilon \left\{ {\exp \left[{-\frac{1}{m}{{\left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)}^m}} \right]} \right\}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant \varepsilon \leqslant {\varepsilon _{{\rm{pk}}}}} \\ {{\sigma _{{\rm{pk}}}}\exp \left( { - \frac{1}{2}{{\left( {\ln \left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)/t} \right)}^2}} \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon \geqslant {\varepsilon _{{\rm{pk}}}}} \end{array}} \right. $ | (8) |
损伤变量D的表达式为:
| $ D = \left\{ {\begin{array}{*{20}{c}} {1 - \exp \left[{-\frac{1}{m}{{\left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)}^m}} \right]\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0 \leqslant \varepsilon \leqslant {\varepsilon _{{\rm{pk}}}}} \\ {1 - \frac{{{\sigma _{{\rm{pk}}}}}}{{E\varepsilon }}\exp \left( { - \frac{1}{2}{{\left( {\ln \left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)/t} \right)}^2}} \right)\;\;\;\;\;\;\;\;\;\;\;\varepsilon \geqslant {\varepsilon _{{\rm{pk}}}}} \end{array}} \right. $ | (9) |
式中:E为弹性模量;σpk为峰值应力;εpk为峰值应变;

|
图 11 试验曲线与拟合曲线对比 Figure 11 Comparison between test curve and fitting curve |
文中用D来表征损伤变量,对试验数据利用式(9) 计算的损伤变量变化规律曲线见图 12和图 13。

|
图 12 不同围压下损伤变量D随加载速率的变化 Figure 12 Changes in damage variables with loading rates under different confining pressures |

|
图 13 不同加载速率下损伤变量D随围压的变化 Figure 13 Changes in damage variables with confining pressures under different loading rates |
从图 12可知,损伤变量D随应变的增加有相同的变化规律。但当加载速率增大时,曲线的增长速度变慢,也就是说D值的增长速度减缓。产生这种现象的原因是:加载速率较高时,混凝土的破坏是按照最短路径的原则发生,因此产生较少的裂纹,损伤也相对较小。从图 13得知,损伤变量D随应变的增长亦有相同的变化规律。当围压增大时,曲线的增长速度变慢,即D值的增长速度降低,但损伤极限差值越来越大。究其原因,由于围压的存在并随围压增大,外部围压水在破坏前期更快进入混凝土内部,孔隙中含水量增大,导致混凝土黏性效应增强,阻碍试件横向变形,延缓了裂缝的发展,损伤变化趋势变缓。
4 结语通过对历经荷载循环历史的水饱和混凝土在不同围压下的常三轴抗压性能试验研究,得出如下结论:
(1) 水饱和混凝土的峰值应力随加载速率的增大而增大;其峰值应力亦随围压的增大而增强。通过对试验数据进行线性回归分析,得到了历经荷载循环后混凝土动态峰值应力与围压、加载速率有关的经验式。
(2) 水饱和混凝土的峰值应变随加载速率的增大整体上呈增大趋势;其峰值应变随围压的增长表现为增大趋势。对数据进行分析,得到了历经荷载循环后混凝土动态峰值应变与围压、加载速率有关的经验式。
(3) 基于Weibull-Lognormal损伤本构模型,研究了损伤变量D的变化规律:随着加载速率的增大,损伤变量D的增长速度减缓;随着围压的增大,D值的增长速度亦降低,但损伤极限差值越来越大。
| [1] |
BUTLER J. The influence of pore pressure upon concrete[J]. Magazine of Concrete Research, 1981, 33(114): 3-17. DOI:10.1680/macr.1981.33.114.3 |
| [2] |
XUAN H V, MALECOT Y, DAUDEVILLE L, et al. Experimental analysis of concrete behavior under high confinement: Effect of the saturation ratio[J]. International Journal of Solids and Structures, 2009, 46(5): 1105-1120. DOI:10.1016/j.ijsolstr.2008.10.015 |
| [3] |
CHEN Z, HU Y, LI Q, et al. Behavior of concrete in water subjected to dynamic triaxial compression[J]. Journal of Engineering Mechanics, 2010, 136(3): 379-389. DOI:10.1061/(ASCE)0733-9399(2010)136:3(379) |
| [4] |
彭刚, 王乾峰, 梁春华. 有压孔隙水环境中的混凝土动态抗压性能研究[J]. 土木工程学报, 2015, 48(1): 11-18. ( PENG Gang, WANG Qianfeng, LIANG Chunhua. Study on dynamic compressive properties of concrete under pore water pressure environment[J]. China Civil Engineering Journal, 2015, 48(1): 11-18. (in Chinese)) |
| [5] |
BRVHWILER E, WITTMANN F H. Failure of dam concrete subjected to seismic loading conditions[J]. Engineering Fracture Mechanics, 1990, 35(1/3): 565-571. |
| [6] |
林皋, 周洪涛, 黄承逵. 循环加载历史对混凝土断裂特性影响的试验研究[J]. 水利学报, 1994(5): 25-30. ( LIN Gao, ZHOU Hongtao, HUANG Chenkui. Experimental study of the effect of cyclic loading history on the fracture properties of concrete[J]. Journal of Hydraulic Engineering, 1994(5): 25-30. (in Chinese)) |
| [7] |
林皋, 王哲, 逯静洲, 等. 三向等压荷载历史对混凝土的强度和变形特性影响的研究[J]. 水力发电学报, 2001(3): 31-41. ( LIN Gao, WANG Zhe, LU Jingzhou, et al. Effect of triaxial equi-compressional loading history on the strength and deformation behavior of concrete[J]. Journal of Hydroelectric Engineering, 2001(3): 31-41. (in Chinese)) |
| [8] |
肖诗云, 张剑. 荷载历史对混凝土动态受压损伤特性影响试验研究[J]. 水利学报, 2010, 41(8): 943-952. ( XIAO Shiyun, ZHANG Jian. Experiment study on effect of load histories on dynamic compressive damage behaviors of concrete[J]. Journal of Hydraulic Engineering, 2010, 41(8): 943-952. (in Chinese)) |
| [9] |
梁春华. 水压作用下的混凝土率效应研究[D]. 宜昌: 三峡大学, 2013. (LIANG Chunhua. The study on rate effect of concrete under hydraulic pressure[D]. Yichang: China Three Gorges University, 2013. (in Chinese))
|
| [10] |
闫东明. 混凝土动态力学性能试验与理论研究[D]. 大连: 大连理工大学, 2006. (YAN Dongming. Experimental and theoretical study on the dynamic properties of concrete[D]. Dalian: Dalian University of Technology, 2006. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10141-2006064872.htm
|
| [11] |
RICHART F E, BRANDTZAEG A, BROWN R L. A study of the failure of concrete under combined compressive stresses[M]. Illinois: University of Illinois, 1928: 185.
|
2. College of Civil Engineering & Architecture, China Three Gorges University, Yichang 443002, China
 2017
2017 
