2. 南京水利科学研究院江苏南京 210029
由于现场条件和施工要求不同,海底管道的铺设方法略有不同,包括直接铺置和埋置(含深埋和浅埋)。但因海床表面凹凸不平,海床土的液化和坍塌及管道附近水动力等因素,无论采取何种铺设方法,海底管道都可能出现局部悬空现象。由于非设计悬空而发生的管道事故,国内外有许多案例,如墨西哥湾的海底管道事故[1],以及我国埕岛油田管道泄漏事故[2],因此在分析海底管道稳定性时,需要重点考虑管道发生悬空的情况。目前对于管道的悬跨长度计算大致有3种方法,即弯矩修正法[3]、涡激振动法[4-5]和线性累积损伤法[6],但上述方法大都考虑线性波作用。由于我国海上石油开采起步较晚,目前大多数油田都建在近海区,因此在管道建设及运行阶段需考虑浅水区波浪等环境影响。大量研究结果表明,在深水区采用线性波浪理论(波高H和波长L关系为H/L→0) 计算误差一般在允许范围内,但对于浅水区,会引起较大的误差[7]。因此研究浅水区管道的悬跨问题时,需充分考虑波浪的非线性影响,深入了解波浪在浅水区的运动特性。目前对非线性波的讨论大多集中在深水区(Stokes波浪理论),根据Le Mehaute[8]的研究成果可知,当水深较浅(波长L与水深d关系为d/L < 0.04) 时,Stokes波浪理论就已经不再适用,可以采用孤立波理论。
1 一阶近似孤立波理论一般取幂级数作为势函数
| $ \phi = \sum\limits_{n = 0}^\infty {{z^n}\phi (x, t)}, {\phi _1}(x, t) = 0 $ | (1) |
若假定在x无穷远处不存在波动,则自由水面z=η+d处的边界条件为:
| $ {\left\{ {\begin{array}{*{20}{c}} {\frac{{\partial \phi }}{{\partial t}} + g\eta + \frac{1}{2}({v_x} + {v_z}) = 0} \\ {\frac{{\partial \phi }}{{\partial z}}\left| {_{z = \eta + d} = \frac{{\partial \eta }}{{\partial t}} + \frac{{\partial \eta }}{{\partial x}} + \frac{{\partial \phi }}{{\partial x}}} \right|} \end{array}} \right._{z = \eta + d}} $ | (2) |
式中:η为波面在静水以上的高度;vx, vz为流场内水质点的水平流速和竖向流速;d为水深。
在研究浅水区波浪时,通常认为水质点的竖向分速远小于水平分速,因此忽略vz的影响,并将vx用线性化水平分速取代,则上述边界条件可转化为:
| $ \left\{ {\begin{array}{*{20}{c}} {\frac{{\partial \phi }}{{\partial t}} + g\eta + \frac{1}{2}\frac{g}{d}{\eta ^2} = 0} \\ {\frac{{\partial \phi }}{{\partial z}} = \frac{{\partial \eta }}{{\partial z}} + \sqrt {\frac{g}{d}} \eta \frac{{\partial \phi }}{{\partial x}}} \end{array}} \right. $ | (3) |
根据上述条件,可得到自由水面非线性影响的二阶近似波动方程:
| $ \frac{{{\partial ^2}\eta }}{{\partial {t^2}}} = gd\frac{{{\partial ^2}\eta }}{{\partial {x^2}}} + gd\frac{\partial }{{\partial x}}\left( {\frac{3}{2}\frac{{{\eta ^2}}}{d} + \frac{{{d^2}}}{3}\frac{{{\partial ^2}\eta }}{{\partial {x^2}}}} \right) $ | (4) |
考虑到浅水区水质点的竖向分速很小,因此忽略vz的影响,只需取一阶近似解:
| $ \eta = H{\text{sech}}^2\left[ {{\sqrt {\frac{{3H}}{{4{d^3}}}} }(x + t\sqrt {g(d + H)} )} \right] $ | (5) |
式中:H为波高,则势函数
| $ \phi = \frac{{2d}}{{\sqrt {3g} }}\tanh \left[{\sqrt {\frac{{3H}}{{4{d^3}}}} ({x}-{t}\sqrt {{g}({d} + {H})} )} \right] $ | (6) |
根据式(6) 可求得波浪场内任意一水质点的水平分速vx为:
| $ {v_x} = \frac{{\partial \phi }}{{\partial x}} = \sqrt {\frac{H}{d}} {\operatorname{sech} ^2}\left[{\sqrt {\frac{{3H}}{{4{d^3}}}} ({x}-{t}\sqrt {{g}({d} + {H})} )} \right] $ | (7) |
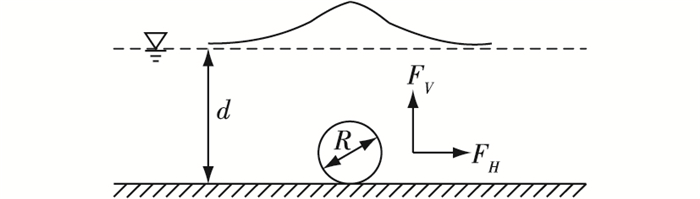
在求解管道允许长度时,需对管道进行受力分析。由于浅水区波浪对管道的影响较大,应充分考虑波浪作用下管道所受的动水作用力,也可以称为波浪力。图 1为波浪力计算模型图,不考虑尾流效应影响,根据Morision方程[10],裸置管道所受的水平力FH和垂直力FV分别为:
|
图 1 计算模型 Figure 1 Calculation model |
| $ {F_{\rm{H}}} = {F_{{\rm{HI}}}} + {F_{\rm{D}}} $ | (8) |
| $ {F_{\rm{V}}} = {F_{{\rm{VI}}}} + {F_{\rm{L}}} $ | (9) |
式中:
根据浅水区的线性假设,忽略vz,根据式(7)~(9) 推导得出浅水区管道悬空段所受波浪力为:
| $ {F_{\rm{H}}} = {F_{{\rm{HI}}}} + {F_{\rm{D}}} = {C_{\rm{M}}}\frac{{{\rm{ \mathsf{ π} }}{\rho _w}H{R^2}}}{{4{d^2}}}\sqrt {3g(d + H)}\text{tanh}\left[ {\sqrt {\frac{{3H}}{{4{d^3}}}} (x + t\sqrt {g(d + H)} )} \right]\\ {\operatorname{sech} ^2}\left[ {\sqrt {\frac{{3H}}{{4{d^3}}}} (x + t\sqrt {g(d + H)} )} \right] + {C_{\rm{D}}}\frac{{{\rho _w}HR}}{{2d}}{\operatorname{sech} ^4}\left[{\sqrt {\frac{{3H}}{{4{d^3}}}} ({x}-{t}\sqrt {{g}({d} + {H})} )} \right] $ | (10) |
| $ {F_{\rm{L}}}+{F_{\rm{L}}}={C_{\rm{L}}}\frac{{{\rho _w}HR}}{{2d}}{\operatorname{sech} ^4}\left[{\sqrt {\frac{{3H}}{{4{d^3}}}} ({x}-{t}\sqrt {{g}({d} + {H})} )} \right] $ | (11) |
由式(10) 和(11) 可以看出,要计算管道所受的动水作用力,也可称作波浪力,必须知道3个参数,即惯性力系数CM、阻力系数CD以及举力系数CL的大小,本文根据文献[10]中提出的参数值进行选取。
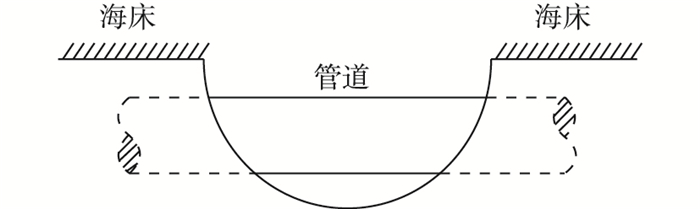
3 海底管道允许悬空长度计算 3.1 悬空形式管道无论是埋置在海床中,还是直铺在海床上,在波流冲刷下都有可能发生悬空,由于海床地形以及海域的环境条件不同,悬空形式也不同。通常浅水区管道受波浪的影响较大,管道铺设较多采用浅埋方式。在这种情况下,埋置管道经过波流的长期冲刷,部分管道会裸露在海床面,而后又在波流的进一步冲刷下发生悬空,管道悬空示意见图 2。
|
图 2 埋置管道常见悬空形式 Figure 2 Common situation of suspended submarine pipelines |
在自身重力(包括配重)和环境荷载作用下,管道的悬空段发生静力及动力响应,当管道周围海流速度较小时,可以考虑采用静力方法计算管道的悬空长度。利用静力法计算管道的允许悬空长度时,往往从管道最大静弯曲应力不超过材料许用应力的角度出发。将计算得到的弯曲应力与材料的许用应力进行比较,得到管道的允许悬空长度。
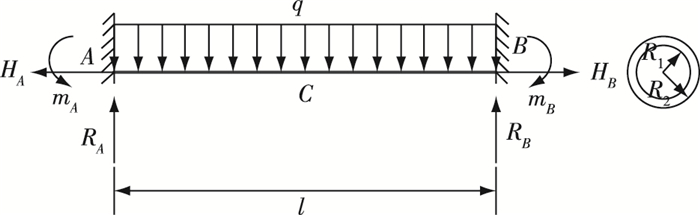
由于管道两端埋置在海床中,可认为管道两端固定,在计算时将单位长度管道上的动水作用力、水下管道单位长度的自重(包括相关配件及输送介质的重量)等外力进行矢量合成,并将该合力以分布荷载的形式作用到管道上,如图 3所示。
|
图 3 悬空管道受力分析示意 Figure 3 Diagram of analysis of forces of suspended submarine pipelines |
考虑管道发生悬空时,管道C点最易发生破坏,因此分析时主要计算该处的弯曲应力。但从图 3可以看出,若要求MC,必须先计算出管道所受的6个未知反力(包括mA,RA,HA,mB,RB,HB),而有效的静力平衡方程只有3个,因此,该问题为3次超静定问题。然而,在小变形的情况下,可以认为沿管道线的水平位移很小,可以忽略不计,即可以忽略水平反力HA与HB。这样就去掉了1个有效的平衡方程,因此,在小变形情况下,有4个未知反力,将问题变为二次超静定问题。
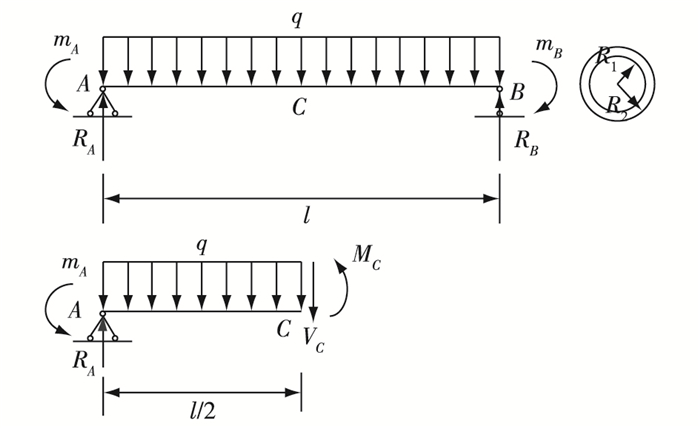
在求解该二次超静定问题时,将两端限制转动的约束去掉,代之以相应的力偶mA,mB,即将图 3中给出的管道受力情况简化为图 4所示。
|
图 4 受力简化示意 Figure 4 Diagram of simplified mechanical model |
根据变形相容条件,可知θA=0,θB=0,得到:
| $ {m_A} = q{l^2}/12, {m_B} = q{l^2}/12 $ | (12) |
式中:l为管跨长度;q为集中荷载,由单位长度管道上的动水作用力FH和FV,以及水下管道单位长度的重力FP(包括相关配件及输送介质的重量)等外力进行矢量合成,
根据平衡方程∑MA=0与∑MB=0,得:
| $ R_A=ql/2, R_B=ql/2 $ | (13) |
式中:MA,MB,RA,RB分别为支点A和B点的弯矩和反力。
假想沿C截面将管切断,保留左端,按正方向假设出C截面上的剪力VC和弯矩MC(见图 4)。根据平衡方程∑Y=0与∑MC=0,得:
| $ V_C=0, M_C=7ql^2/24 $ | (14) |
根据材料力学可知,管道C点横截面上的最大弯曲应力为:
| $ {\sigma _{\max }} = {M_C}/{W_z} $ | (15) |
式中:Wz为抗弯截面系数,对于圆管Wz=4πR23R24-R14,R1为管道内半径,R2为管道外半径。
根据式(14) 与(15),得:
| $ {\sigma _{\max }} \leqslant = \frac{{7q{l^2}}}{{96{\rm{ \mathsf{ π} }}R_2^3(R_2^4 - R_1^4)}} $ | (16) |
在求解管道的允许悬空长度时,认为管道的最大弯曲应力σmax应小于材料的许用应力[σ],即:
| $ {\sigma _{\max }} \leqslant [\sigma] $ | (17) |
根据式(16) 与式(17),给出允许悬空长度计算式:
| $ {l_{\max }} = \sqrt {\frac{{96{\rm{ \mathsf{ π} [}}\sigma {\rm{]}}R_2^3(R_2^4 - R_1^4)}}{{7q}}} $ | (18) |
根据孤立波理论,得到管道允许悬空长度为:
| $ {l_{\max }} = \sqrt {\frac{{96{\rm{ \mathsf{ π} [}}\sigma {\rm{]}}R_2^3(R_2^4 - R_1^4)}}{{7{{[{F}_{\rm{H}}^2 + {{({F_V} + {F_P})}^2}]}^{1/2}}}}} $ | (19) |
某油田位于渤海湾,目前年产原油近100万t。自2008年8月首条海底管道埋设投产运行以来,工程海区海床普遍呈现整体冲刷态势,部分埋设管道已出现了裸露、悬空现象,其中1-1#~1-3#人工岛之间的海底输油管道出现大面积吸沙区,且吸沙区内海底输油管道出现大范围悬空(见图 5),管道悬空状况见表 1。当管道悬空长度达到一定值时,管道较容易失稳,甚至发生重大安全事故,造成油田停产、生态环境破坏等严重后果,因此需要对悬空的海底管道进行定期维护和处理,但由于海上施工作业成本高,难度大,可以对处于悬空但在安全允许悬空范围内的管道暂不进行加固,以节省施工成本,因此需要计算管道的允许悬空长度。

|
图 5 悬空管道现状 Figure 5 Present situation of suspended pipelines |
管道材料为X65Q,密度为7 850 kg/m3,弹性模量为207 GPa。其中混输管道采用双管结构,外管直径660 mm,内管直径508 mm,供水管道直径356 mm。根据API 5I PSL2标准可知X65钢管材料许用弯曲应力为327 MPa。计算时采用的波浪要素为考虑冲刷最严重的情况,分别计算设计波浪50年、5年、2年重现期时海底管道允许悬空长度。波浪要素具体数值[12]为:水深d为5 m,海水密度ρw为1 030 kg/m3,50年、5年、2年重现期的波长L分别为80.0,70.3和65.2 m;周期T分别为8.8,8.3和7.8 s,波高H分别为4.69,3.94和3.67 m。
根据式(19) 计算得混输管道50年、5年和2年重现期的允许悬空长度分别为35.42,35.31和35.27 m;供水管道相应的允许悬空长分别为30.504, 30.528和30.605 m。可见,计算得到混输管道允许悬空长度大约为35 m;供水管道的允许悬空长度相对较小,允许悬空长度大约为30 m。而从表 1可以看出,目前混输管道有两段大于允许悬空长度,供水管道有一段大于允许悬空长度。这些管道存在严重的安全隐患,一旦结构损坏,必将造成极大的经济损失和生态破坏,应对这些管道进行及时处理。
5 结语根据浅水区波浪特点,基于一阶近似孤立波理论,利用Morison方程推导出浅水区海底管道悬空段所受波浪力的求解公式。针对常见的悬空形式,基于材料力学理论,从管道最大静弯曲应力不超过材料许用应力的角度出发,计算出管道的最大弯曲应力,并与材料的许用应力进行比较,进一步推导出浅水区管道允许悬空长度的计算式。最后,根据推导公式计算出渤海湾某油田海底管道的允许悬空长度。据相关资料可知,目前该海区有部分管道已超过计算的允许悬空长度,应对其进行加固处理,以免发生事故,造成不必要的经济损失和生态破坏。
| [1] |
赫比希J B. 海底管道设计原理[M]. 北京: 石油工业出版社, 1988. ( HERBICH J B. Principle of submarine pipeline design[M]. Beijing: Petroleum Industry Press, 1988. (in Chinese))
|
| [2] |
许文兵. 平湖油气田海底输油管线临时修复方法[J]. 中国海洋平台, 2003, 18(2): 37-40. ( XU Wenbing. The temporary repairing method for sub-sea oil pipeline of Pinghu oil and gas field[J]. China Offshore Platform, 2003, 18(2): 37-40. (in Chinese)) |
| [3] |
王维. 确定海底埋设输油管线允限冲刷长度的一种实用方法[J]. 西南石油学院学报, 1996, 18(3): 94-97. ( WANG Wei. A practical method of obtaining allowable erosion length of sea-bottom imbeded oil pipeline[J]. Journal of Southwestern Petroleum Institute, 1996, 18(3): 94-97. (in Chinese)) |
| [4] |
马良. 海底管道在水流作用时诱发的振动效应[J]. 中国海洋平台, 2000, 15(2): 30-35. ( MA Liang. The vibration effect of subsea pipelines under the effect of water[J]. China Offshore Platform, 2000, 15(2): 30-35. (in Chinese)) |
| [5] |
FURNES G K, BEOTSEN J. On the response of a free span pipeline subjected to ocean currents[J]. Ocean Engineering, 2003(30): 1553-1557. |
| [6] |
DNV-OS-F101 Submarine pipeline systems[S].
|
| [7] |
SUDHAN C M, SUNDAR V, RAO S N. Wave induced forces around buried pipeline[J]. Ocean Engineering, 2002, 29(5): 533-544. DOI:10.1016/S0029-8018(01)00012-9 |
| [8] |
MÉHAUTÉB L. An introduction to hydrodynamics and water waves[M]. New York: Springer-Verlag, 1976.
|
| [9] |
邱大洪. 波浪渗流力学[M]. 北京: 国防工业出版社, 2006. ( QIU Dahong. Wave percolation mechanics[M]. Beijing: National Defence Industry Press, 2006. (in Chinese))
|
| [10] |
范运林. 作用在海底管线上的波浪力[J]. 海洋科学, 1983(6): 1-7. ( FAN Yunlin. Wave forces on submerged pipelines near the sea-bottom[J]. Marine Science, 1983(6): 1-7. (in Chinese)) |
| [11] |
李春雨. 南堡油田人工岛海底管线悬空分析及治理[J]. 内江科技, 2012(1): 113-119. ( LI Chunyu. The analysis and control of submarine pipeline of artificial island of South Fort Oilfield[J]. Neijiang Science and Technology, 2012(1): 113-119. (in Chinese)) |
| [12] |
河流海岸研究所. 冀东南堡油田1#构造水域波浪数模推算报告[R]. 南京: 南京水利科学研究院, 2014. (Institute of River and Coastal Research. The calculation report of wave mathematical model for 1# waters in Nanpu Oilfield[R]. Nanjing: Nanjing Hydraulic Research Institute, 2014. (in Chinese))
|
2. Nanjing Hydraulic Research Institute, Nanjing 210029, China
 2017
2017 
