2. 北京市勘察设计研究院有限公司, 北京 100038
随着近30年来国内外城市建设中地下水位回升事件频繁发生,由此引起的结构上浮、变形甚至破坏的案例屡见不鲜[1-2],抗浮措施在地下结构中逐渐得到重视,总体上可以分为主动抗浮(如排水减压、帷幕隔水等)与被动抗浮(如抗浮桩、抗浮锚杆、结构配重等)两类[2-5]。而相对发达国家抗浮而言,受目前技术经济条件制约,我国还是以被动抗浮措施为主,其安全性和造价很大程度上取决于抗浮水位(部分文献称为“抗浮设防水位”、“抗浮设计水位”或“抗浮设防水头”等,方便起见,统一称为“抗浮水位”)这一重要技术经济指标,相关研究在我国今后相当一段时间内也具有重要的理论与现实意义。
我国抗浮水位研究最早可追溯到20世纪90年代中期,针对1995年官厅水库放水造成北京市西郊区域性的地下水位回升,引起部分地下室开裂和渗水工程事件,张在明等[3, 6-7]率先在北京地区开始了有关抗浮水位问题的系统研究,首次将孔隙水压力分布和地下水水位预测等科学方法引入到抗浮水位分析中,并在大量的长期观测地下水数据基础上,首次建立了抗浮水位分析的场域法分析方法体系,且在北京地区得到了广泛应用。张旷成首次在规范中对抗浮水位做了比较明确的定义[8],提出了“场地抗浮水位”概念,并对相关分析方法展开了较深入讨论[9]。黄志仑对多层含水层的抗浮水位及扬力分析方法进行了较详细讨论[10-11]。此后,许多学者在此基础上从不同专业领域(如水文地质、土力学和结构工程等)开展了进一步的研究工作,抗浮水位研究也逐渐成为岩土工程与结构工程领域的一个热点。
但是,由于抗浮水位是一个十分复杂的问题,涉及到水文地质、工程地质、土力学、水力学和结构工程等多个学科领域,再加上我国地域辽阔,气象水文条件、地质及岩土条件和城市水资源分布等因素差异较大,因此迄今为止,结构抗浮水位尚远未形成相对统一而严谨的概念、方法和技术体系,从而在工程实践中多以经验为主,人为性很大,分歧较多,且目前的研究成果缺乏延续性和系统性,影响了对该问题进一步聚焦和深入研究。为此,通过系统搜集相关的典型研究成果,从抗浮水位的基本概念、抗浮水位分析中两个基本问题(孔隙水压力和最高水位预测)的方法论和抗浮水位分析技术体系等3个行业关注和争论的焦点进行全面综述与科学评论,以期达到消除行业内学术观点的“隔阂”、“形成认识上统一”和“集百家之长”目的,从而推进我国抗浮水位研究与实践朝着更科学和规范的方向发展。
1 抗浮水位基本概念“抗浮水位”这个词最早来源于地表水防洪领域的“设计水位”[12]或“设防水位”,但由于地下水的赋存及运动规律较地表水要复杂得多,因此在其概念认识上目前还远不及防洪领域“设防水位”那样统一,这也是造成当前抗浮水位研究存在较大争议的根源之一。囿于篇幅,主要对如下3种代表性的抗浮水位概念进行综述与评论。
1.1 二维抗浮水位文献[8]首次对“抗浮水位”在规范中进行了明确定义,提出了“场地抗浮设防水位”概念,该规范主编张旷成后来在文献[9]中对此展开了进一步论述,强调一个场地只有一个抗浮水位,对于多层含水层区,抗浮水位为各层地下水最高水位的最高值,而和建筑物基底位于哪个含水层无关,因此称其为“二维抗浮水位概念”,最终可用式(1) 表达,即
| $H = {\rm{Max}}[{H_{{\rm{mi}}}}\left( {x,{\rm{ }}y} \right)]\quad i = 1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \ldots ,n$ | (1) |
式中:H为抗浮水位标高[L];Hmi为第i层含水层的最高水位标高[L];x, y为建筑场地的平面坐标[L];n为含水层数。
二维抗浮水位概念是一个独立于建筑基底埋深而客观存在的水文地质学意义上“场地最高水位”问题,这是一种最直观的抗浮水位概念,并和美国国家预制混凝土协会(NPCA)的建议[13]基本一致。从式(1) 可以看出,二维抗浮水位是一个“纯水位”概念,本身不含“浮力”意义(而是计算浮力的一个条件),将抗浮水位分析聚焦在“最高水位预测”上[9],这比较符合传统水文地质工作的特点,对简化和推进抗浮水位分析工作有重要意义。二维抗浮水位概念在单一含水层区和各层地下水位十分接近条件下多层含水层区均比较适用,但当多层含水层之间最高水位差异明显时(如北京地区)[6],可能出现过于保守情况。
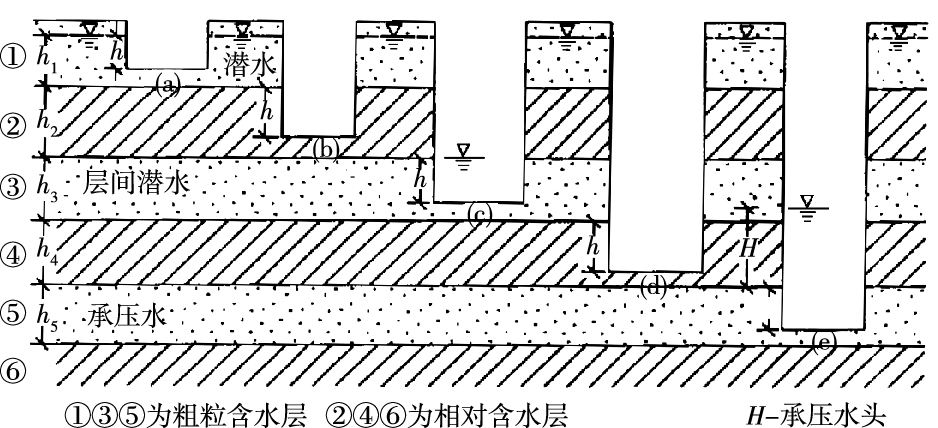
1.2 准三维抗浮水位针对文献[8],黄志仑提出了完善性建议,认为在多层地下水区,抗浮水位应按建筑基底所在层位地下水的最高水位取值[10],同时对于含水层之间的相对弱透水层中的孔隙水压力(原文中称“扬力”)的计算也有所考虑[11]。根据黄志仑的观点和Bernoulli方程(略去速度水头,下同),抗浮水位可用下式表达,即
| $H = \left\{ {\begin{array}{*{20}{l}} {{H_{{\rm{mi}}}}\left( {x,{\rm{ }}y} \right),}&{i = 1,{\rm{ }}2,{\rm{ }}3,{\rm{ }} \ldots ,n{\rm{ }}(当基底位于第i含水层中)}\\ {{z_{\rm{b}}} + \frac{{{P_{{\rm{mj}}}}(x,{\rm{ }}y,{\rm{ }}{z_{\rm{b}}})}}{{{\gamma _{\rm{w}}}}},}&{j = 1,{\rm{ }}2,{\rm{ }}3, \ldots ,m{\rm{ }}(当基底位于第j弱透水层中)} \end{array}} \right.$ | (2) |
式中:zb为基底位置标高[L];Pmj(x, y, zb)为基底标高zb处第j弱透水层最大孔隙水压力,由其上、下相邻含水层的最高水位确定[ML-1T-2];γw为水的重度[ML-2T-2]。
显然,和式(1) 相比,式(2) 考虑到了多层地下水水位和层间弱透水层的孔隙水压力,在含水层中仍为“水位”的概念,而在弱透水层中为“水头”的概念,表明抗浮水位与基底标高zb有关,强调了“力”的意义。同时,由于式(2) 对各含水层和层间弱透水层是独立考虑的(图 1),相当于n个独立的含水层和m个独立的隔水层交错叠加在一起,而不考虑它们之间的联系,因此称其为“准三维抗浮水位概念”。相对于二维抗浮水位概念,准三维抗浮水位概念在多层含水层区比较合理,尤其考虑到了不同含水层和层间弱透水层之间的差异,但由于对每个含水层和弱水层是独立考虑的(图 1),分析时各层地下水均需要有足够的水位监测资料,这在实际应用中可能遇到一定困难,如北京地区的层间水,由于其分布范围小,监测资料又很少,因此其最高水位是很难单独预测的,而需要借助其上下含水层间接求解[3, 6-7, 14]。
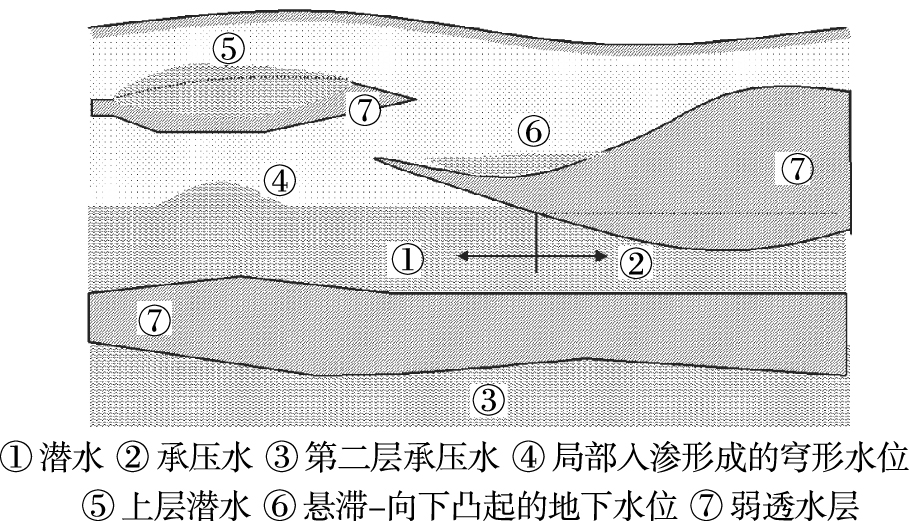
1.3 三维抗浮水位张在明在北京地区长期地下水位监测、科学研究和工程实践基础上,认为抗浮水位不是简单的某个含水层的“最高水位”问题,而是与结构基底所在位置(可能在含水层中,也可能在弱透水层中)不利条件下最大孔隙水压力对应的一种“等效水位”(实际是水头),强调“力”的内涵[6-7],这一点与“准三维抗浮水位概念”有相似之处,但也存在两点明显差别:一是张在明的抗浮水位无论基底位于含水层还是弱透水层,都是“水头”的概念;二是强调各含水层、层间弱透水层之间存在密切水力联系,应按一个完整的“地下水赋存体系”(groundwater regime)来考虑(对比图 2和图 1),其渗流场内任意空间点(x, y, z)的水头H可统一按Bernoulli方程描述,且需用地下水动力学中三维渗流模型来分析才能获得满意的解答,因此称其为“三维抗浮水位概念”。
根据前述三维抗浮水位概念和Bernoulli方程,无论基底位于什么位置(含水层或层间弱透水层),抗浮水位均可以统一按下式表述,即
| $H = {z_{\rm{b}}} + \frac{{{P_{\rm{m}}}(x,{\rm{ }}y,{\rm{ }}{z_{\rm{b}}})}}{{{\gamma _{\rm{w}}}}}$ | (3) |
式中:Pm(x, y, zb)为基底标高zb处最大孔隙水压力,由三维渗流模型分析确定[ML-1T-2]。
因此,从理论上看,三维抗浮概念是建立在较严格的土力学、水力学和地下水动力学等科学理论基础上的,具有普遍适用性和统一性,对抗浮水位科学研究和工程实践具有重要的指导意义。同时,相比二维和准三维来说,三维抗浮水位概念也比较抽象,对渗流建模与分析水平的要求也比较高,并且需要有丰富的地下水位(或孔隙水压力)监测资料作支撑。而二维和准三维抗浮水位概念是对三维抗浮水位概念特定条件下的简化,因此在一定意义上说具有降低抗浮水位分析工作难度的作用。
上述3种抗浮水位概念虽然存在差别,但都涉及到两个基本问题,这两个问题也是抗浮水位分析的热点和焦点,即:① 基底孔隙水压力分布规律和浮力计算问题,这是基底位于弱透水层中抗浮水位分析时常遇到的问题;② 地下水最高水位预测问题,这是基底位于含水层中时抗浮水位分析所遇到的问题。
2 弱透水层孔隙水压力分布规律大量的试验、工程实践都证实有效应力原理对于饱和土近于完美地反映了实际情况[6],但由于我国地层性质差别很大(如沿海地区的软土和内陆的冲洪积扇地层),往往在实际应用中会遇到许多具体问题,尤其在多层含水层区,由于地下水赋存和运动的复杂性,其水压力具体分布会与静水压力存在很大区别,这一点包括上述3种抗浮水位概念在内的许多学者认识都是比较一致的,即所谓弱透水层中孔隙水压力的“折减”问题,但在“折减”的机理和计算方法目前还十分不统一,总体上分为如下两类。
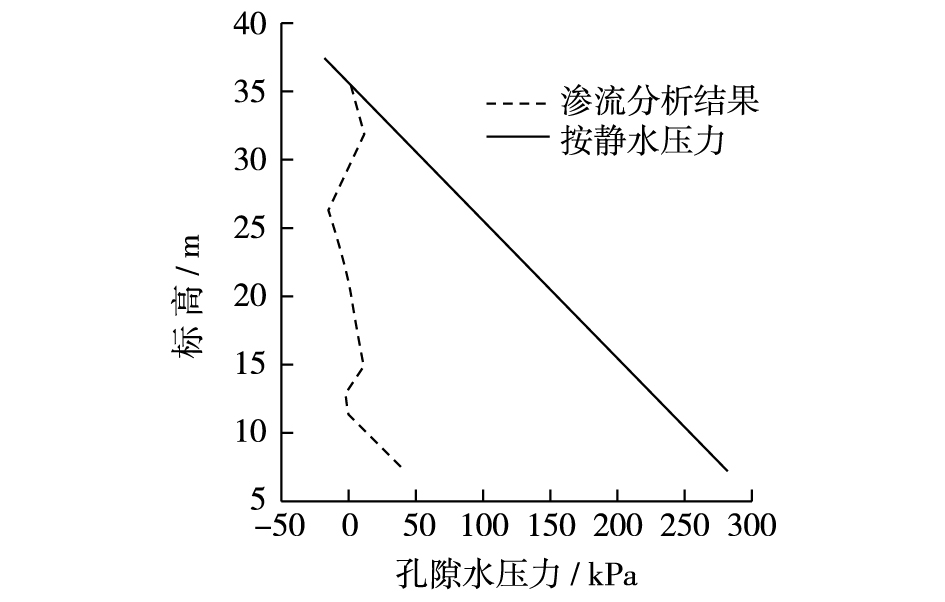
2.1 孔隙水压力折减问题的渗流分析法该方法是基于有效应力原理和渗流理论上的经典理论方法[6, 15]。张在明等根据“渗流孔隙水压力”概念,在北京地区做了大量室内外试验与理论分析工作基础上,提出了第四纪冲洪积扇地区地层中孔隙水压力分布的垂向一维饱和-非饱和渗流模型(图 3),该观点认为,由于多层含水层之间的垂向渗流的发生,式(3) 中的水头H沿z方向出现损失,从而引起孔隙水压力P的减小[2-3],这一重要结论在北京地区得到大量实际监测数据验证并被广泛应用于工程中,同时也被其他学者的研究成果所佐证[15-17],应该说渗流分析方法在以北京地区为典型的冲洪积扇地区具有普遍适用性。
|
图 3 多层含水层中孔隙水压力分布曲线[6-7] Figure 3 Distribution curves of pore water pressure in multilayered aquifer[6-7] |
同时,在工程实践上,利用渗流分析方法得到的孔隙水压力要比静水压力明显小(图 3),以此进行抗浮设计比较经济,因而具有重要工程意义。
2.2 关于结合水引起孔隙水压力折减问题渗流理论和有效应力原理是经典理论,但由于弱透水层的孔隙较小,受结合水等内部结构因素影响[9],连通性不及粗颗粒含水层好,这就引起了针对经典的渗流分析方法在弱透水层中是否适用问题的争论,即除了渗流作用以外,结合水是否也会引起孔隙水压力折减问题,目前主要存在如下3类观点:
(1) 结合水引起孔隙水压力折减明显。部分学者研究认为,即使没有渗流情况下,由于结合水造成弱透水层的连通性较差等原因,孔隙水压力也是需要折减的[11, 19-20]。有些学者提出了测定折减系数的相关试验方法,并测出了具体折减系数值,试验结果较明显,甚至能达到65%左右[20]。
(2) 结合水引起孔隙水压力折减不明显。这和观点(1) 正好完全相反,张第轩等通过大量室内试验研究表明,即使是黏性土,其结合水对孔隙水压力折减系数也很小,工程应用中几乎不考虑[15-16, 21]。向科等通过模型试验研究,认为长期稳定状态下,饱和黏性土能完全传递孔隙水压力[22],而无需考虑结合水的影响。
(3) 折减程度主要受强结合水影响,而与弱结合水关系不大。这种观点是(1) 和(2) 的折衷,在逻辑上比(1) 和(2) 更具有普遍性。李广信等认为弱结合水能传递静水压力而强结合水则比较复杂,同时认为塑限含水量是强结合水的上限含水量,当含水量低于塑限含水量时(或液性指数小于0),表明没有弱结合水和自由水,并且通过试验研究当固结压力大于600 kPa时,液性指数小于0,弱结合水很少,静水压力只能传递70%~80%,且需要较长时间[23]。介玉新等得到类似的结论,认为大多数情况下,有效应力原理是足够准确的,但在高压下需要修正,对于液性指数接近或小于0的黏性土,有效应力原理的适用性尚难下结论[24]。宋林辉等通过系统的室内试验研究,认为无论是渗流状态还是静水状态,黏性土内各点孔隙水压力趋于稳定所需时间均受固结压力或水压力影响,在不同压力(固结压力和水压力)条件下又可以互相转化,反映了结合水对孔隙水压力分布影响的复杂性[25]。
从上述研究成果讨论中不难发现一个非常有趣的结论:宋林辉等开始持观点(1) [20],后来研究持观点(3) [25];李广信开始的工作持观点(2) [15],后来研究也持观点(3) [23],因此观点(3) 具有一定普遍性,相对合理。以北京地区为例,饱和弱透水层的液性指数多数在0.25以上,因此弱结合水和自由水起的作用大,孔隙水压力分布规律比较符合经典的有效应力原理和渗流理论,观点(3) 蜕化成观点(2),这也从另一个角度解释了图 3中垂向一维渗流模型与实测结果吻合的原因[6]。至于其他地区抗浮水位分析中的孔隙水压力是否需要考虑结合水的影响,则是一个十分复杂的问题,需要根据地区地层的物理力学性质,在有针对性的现场监测、室内试验基础和系统的理论研究基础上综合确定,而不可轻易根据观点(1) 进行折减。
3 远期最高地下水位预测问题地下水远期最高水位预测是抗浮水位分析的另一项重点和难点工作,下面对目前主要采用的3类方法进行简单介绍。
3.1 历史最高水位法用历史最高地下水位作为远期最高水位预测值应该说是一种比较常用的方法,许多文献都有不同程度的涉及[6-7, 9-10],尤其是地下水位监测时间序列较长,且地下水位动态规律比较简单的情况下,其主要优点是依据实测资料,在直观上具有较好的说服力(如北京地区的1959年最高水位)。但从本质上看,历史水位并不等于远期水位,前者代表地下水位动态规律的“过去时”,后者代表地下水动态规律的“将来时”,当有些地下水影响因素不可再现情况下,地下水位动态规律会出现不可逆转的发展趋势。文献[6]和[7]用历史最高水位来预测北京地区的台地潜水和上层滞水的远期最高水位,这主要是因为这两种类型的地下水主要影响因素是多年来变化不大的气象条件,而对于受人为因素影响较大的潜水~承压水,则认为历史最高水位法会过于保守。另一方面,事实证明,历史最高水位法也未必最安全,以英国伦敦为例,由于1965年以后地下水开采量锐减,地下水出现快速回升,2003年有的地区甚至超过了100年以来的历史最高水位[3]。因此,历史最高水位法不是严格意义上的水位预测方法,在实际应用中需要根据地下水位动态规律不同区别对待。
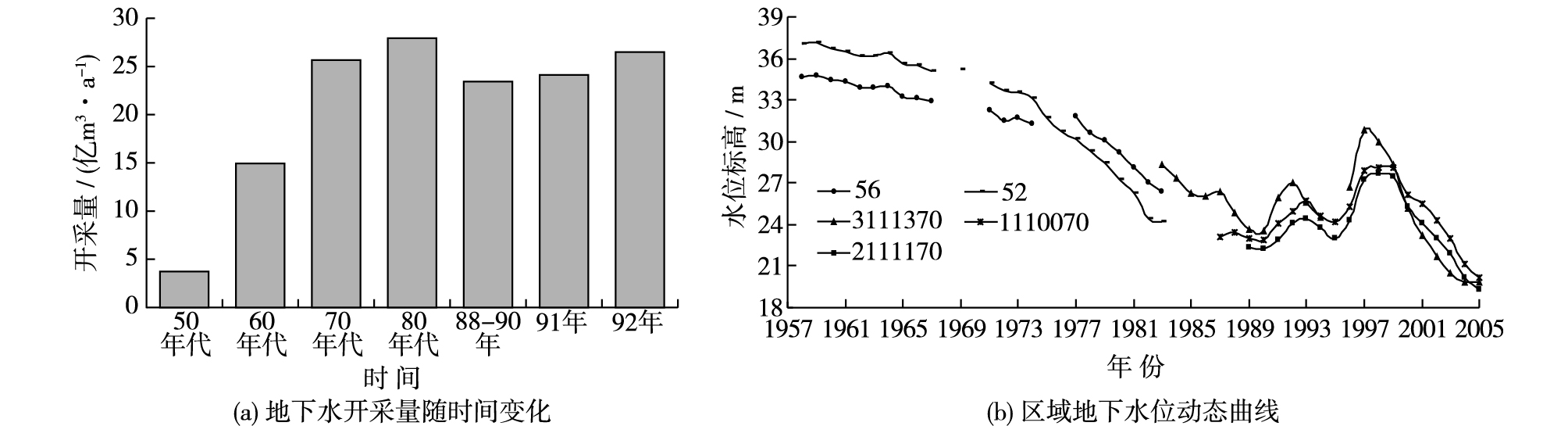
3.2 基于宏观数据反演方法该方法基本思路是根据地下水监测网获得地下水水位观测数据生成等值线图和动态曲线图,以此识别不同区域内各水文年中地下水位的主要影响因素(如图 4中地下水开采量),进而定量反演出的影响因素对地下水影响程度作为模型参数,然后利用工程类比法,找出未来影响因素和当前影响因素之间的换算关系,最后将未来影响因素作为预测输入条件,实现远期最高水位的预测。
|
图 4 基于宏观数据反演预测法(以北京地区开采量与地下水位动态之间关系为例) Figure 4 Prediction method of groundwater level with inversion based on macro data (taking relationships between groundwater withdrawal and groundwater level dynamics in Beijing area as an example) |
基于宏观数据反演是以大量实测数据分析为基础的,因此具有较好的可靠性,但同时又是一种对数据样本依赖性较强的半经验方法,主要适合于单个点状建筑[6-7, 26]。
3.3 数值方法数值方法在水文地质学中是较经典的水位预测方法,但传统的地下水数值模型主要目的是为水资源管理和环境保护服务,预测精度尚不足以满足工程需要,尤其是模型中没有充分反映对抗浮水位有直接影响的浅层地下水(一般指50 m深度以内)的复杂分布规律[27-28]。针对前述抗浮水位分析的现状,以及北京城市建设的迫切需要,沈小克等在充分研究北京地区浅层地下水区域分布特征基础上,首次建立了北京中心城1 100 km2范围的区域浅层地下水三维渗流模型[3, 29],利用大量实测数据进行模型识别与验证,对远期水位预测思路进行研究,在此基础上提出了抗浮水位分析的区域法,并在北京地区多个重大工程中得到很好应用。安振东等[30-31]分别利用有限差分法和有限单元法对青岛和昆明市一些具体工程的场地含水层最高水位进行了预测,取得了很好效果。
数值方法最大的优点是可对各种复杂的边界条件有较强的适应性,同时,当这些条件发生变化时,需要对模型进行及时更新与维护。
4 抗浮水位分析方法技术体系技术体系是对前述概念和方法论在工程实践中的一种具体实现与应用。目前虽然我国针对具体工程的抗浮水位分析例子较多,但由于前述抗浮水位基本概念和两个基本问题方法论分歧较多,工程实践中一般是具体问题具体分析,多数地区缺乏相对统一的技术体系。北京地区由于工作开展较早,形成了以场域法和区域法最为典型的技术体系,同时近几年其他地区也开始尝试了技术体系的建立与应用。
4.1 场域法虽然早在1990年代中期张在明提出三维抗浮水位概念,但限于当时的工作条件,建立三维渗流模型比较困难,为满足当时建设的迫切需要,提出一种“间接”的技术方法体系,分如下两步来实现:首先通过基于宏观数据反演的水位预测方法(图 4)预测场地的最高水位,然后通过垂向一维渗流孔隙水压力分布模型(图 3)来分析建筑场地不同深度内的最大水头(孔隙水压力)[6-7, 17]。该方法主要适用单个建筑,因此称其为“场域法”,在北京地区得到了广泛应用,最近,蔡国成等也利用类似方法尝试建立宁波平原地区的抗浮水位分析技术体系[26]。对跨度较大的地下工程(如地铁等),场域法分析工作量较大,且很难保持分析结果在空间上的协调性,同时对一些重要条件的变化缺乏很好的适应性。
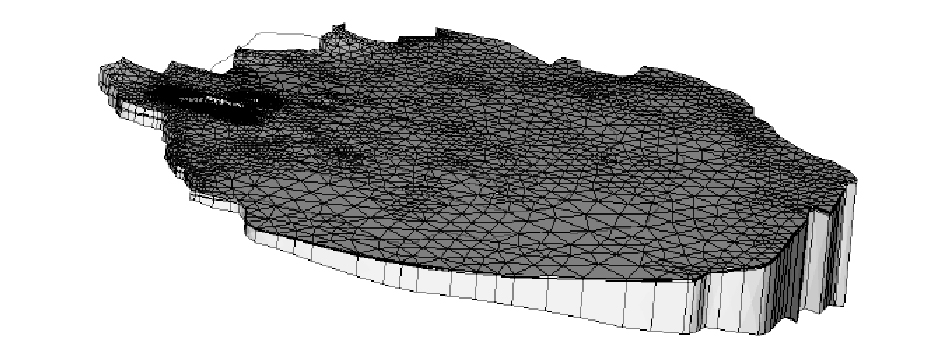
4.2 区域法该方法体系是基于区域地下水三维瞬态流模型(图 5),因此称其为区域法[3, 29-30],是对三维抗浮水位概念的一种直接实现。区域法基本思路是,利用区域地下水位最新监测资料代入区域地下水三维瞬态流模型中,预测空间任一点的最高水头(或最大孔隙水压力),然后得到结构基底处的最高水头(或孔隙水压力),从而实现抗浮水位分析,具有普遍适用性和较强实用性。同时,为提高模型精度,对于地下水分布条件复杂的地区,需要将三维模型(如图 5)与一维渗流模型(如图 3)进行相互校核,得到更合理的抗浮水位分析结果。区域法是目前相对科学和统一的方法,但需要大量的数据对数值模型进行不断改进和维护。沈小克等利用区域法对北京某工程抗浮水位进行了分析[29],安振东对青岛啤酒城改造工程的抗浮水位进行了分析[30],均获得满意结果。
|
图 5 北京市中心城三维瞬态流有限元剖分 Figure 5 Scheth of meshing by 3D FEM in Beijing central city |
20多年以来,由于城市地下空间开发的迫切需要,结构抗浮水位研究在我国逐渐受到重视,并取得了较大进展,但由于抗浮水位问题自身的复杂性,目前的主要研究成果尚未形成相对统一的理论、方法或技术体系,存在较大分歧,同时,这些研究成果具有各自的优点和需要改进的地方。通过对这些研究成果进行科学综述,得到如下几点主要结论:
(1) 在抗浮水位概念方面,总体上可以分为二维、准三维和三维等3种类型,三者主要区别在“水位”和“水头”上以及问题求解思路上。三维抗浮水位概念是建立在相对严谨的土力学和地下水动力学基础上的,而二维及准三维是在某种特定的条件下对三维抗浮概念的一种简化。在科学研究和工程实践中需要深刻理解这三种抗浮水位概念之间的关系,并根据具体问题的难易程度灵活运用。
(2) 在孔隙水压力分析方面,基于渗流理论的经典分析方法在以北京为代表的冲洪积扇地区具有普遍适用性;而基于结合水对孔隙水压力影响问题较复杂,主要受控于强结合水,目前的研究成果在抗浮水位分析中的适用性尚需要慎重考虑。
(3) 在远期最高水位预测方面,历史最高水位法是目前常用的地下水位预测方法之一,但历史水位并不完全等同于远期水位,尤其是有些条件出现不可再现情况下,因此需要根据地水下位动态规律不同而区别对待;基于宏观数据反演预测是一种半经验方法,在北京地区有了较好的应用,且在其他地区也有尝试,但主要适用于单体建筑;数值方法是理论上相对最完善的方法,但需要大量资料和数据作为建模分析的支持,同时模型也需要根据最新数据不断维护。
(4) 在抗浮水位分析技术体系方面,以场域法和区域法为代表的技术体系在北京地区得到很好应用与推广,其他地区也有了一定尝试,为我国抗浮水位分析工作朝着科学化、规范法方向发展提供了借鉴。和发达国家相比,我国目前的技术经济水平还有较大距离(发达国家经济实力较雄厚,抗浮水位一般可直接取接近地表的位置,或采用与抗浮水位关系不大的主动抗浮措施),抗浮水位分析将是今后相当长一段时间内十分重要的工作。
为推进未来抗浮水位分析工作的科学化和规范化,除了需要对目前工作取长补短外,还需进行如下的进一步探讨性工作:
(1) 加强相关机理研究和分析方法自身的(如孔隙水压力分布和远期最高水位预测)科学研究,形成相对统一而科学严谨的基本理论和分析方法。
(2) 加强区域性地下水位长期监测和孔隙水压力分布特征的室内外试验研究,积累丰富的基础性资料,并利用现代数据管理技术进行数据动态管理,为该地区水位及孔隙水压力变化提供实时预警服务。
(3) 建立某个地区地下水区域性数值模型,为该地区抗浮水位分析提供依据。
(4) 充分考虑地区的地质及水文地质特点、水资源政策和抗浮设计施工技术特点,在上述工作基础上,进行系统的科学研究与工程实践,最终形成适合于某个地区或某些地区相对较统一和实用的抗浮水位分析技术体系或地方性技术标准。
| [1] |
BRASSINGTON F C. Rising groundwater levels in the United Kingdom[C]//Proceedings of the Institution of Civil Engineers, London: Nabu Press, 1990: 1037-21057.
|
| [2] |
贾益纲, 费逸, 吴光宇, 等. 某大型地下室结构上浮拱起工程事故分析与处理[J]. 施工技术, 2016, 45(16): 48-52. ( JIA Yigang, FEI Yi, WU Guangyu, et al. Analysis and processing on up-floating arch accident of a basement structure[J]. Construction Technology, 2016, 45(16): 48-52. DOI:10.7672/sgjs2016160048 (in Chinese)) |
| [3] |
沈小克, 周宏磊, 王军辉, 等. 地下水与结构抗浮[M]. 北京: 中国建筑工业出版社, 2013. ( SHEN Xiaoke, ZHOU Honglei, WANG Junhui, et al. Groundwater and anti-buoyancy of engineering structures[M]. Beijing: China Construction Industry Press, 2013. (in Chinese))
|
| [4] |
唐孟熊, 胡贺松, 张程林. 地下结构抗浮[M]. 北京: 中国建筑工业出版社, 2016. ( TANG Mengxiong, HU Hesong, ZHANG Chenglin. Anti-buoyancy of underground structures[M]. Beijing: China Construction Industry Press, 2016. (in Chinese))
|
| [5] |
古今强, 侯家健. 关于基础设计中地下水浮力问题的思考[J]. 建筑结构, 2014, 44(24): 133-138. ( GU Jinqiang, HOU Jiajian. Thoughts on uplift pressure of underground water in foundation design[J]. Building Structure, 2014, 44(24): 133-138. (in Chinese)) |
| [6] |
张在明. 地下水与建筑基础工程[M]. 北京: 中国建筑工业出版社, 2001. ( ZHANG Zaiming. Groundwater and building foundation engineering[M]. Beijing: China Construction Industry Press, 2001. (in Chinese))
|
| [7] |
张在明, 孙保卫, 徐宏声. 地下水赋存状态与渗流特征对基础抗浮的影响[J]. 土木工程学报, 2001, 34(1): 73-78. ( ZHANG Zaiming, SUN Baowei, XU Hongsheng. Effect of characteristics of ground water distribution and seepage on anti-uplift analysis of building foundations[J]. China Civil Engineering Journal, 2001, 34(1): 73-78. (in Chinese)) |
| [8] |
JGJ72—2004/J366—2004高层建筑岩土工程勘察规程[S]. (JGJ72—2004/J366—2004 Specification for geotechnical investigation of tall buildings[S].(in Chinese))
|
| [9] |
张旷成, 丘建金. 关于抗浮设防水位及浮力计算问题的分析讨论[J]. 岩土工程技术, 2007, 21(1): 15-20. ( ZHANG Kuangcheng, QIU Jianjin. Analysis and discussion on water level for prevention of up-floating and calculation of upljft pressure[J]. Geotechnical Engineering Technique, 2007, 21(1): 15-20. (in Chinese)) |
| [10] |
黄志仑, 马金普, 李丛蔚. 关于多层地下水情况下的抗浮水位[J]. 岩土工程技术, 2005, 19(4): 182-183, 217. ( HUANG Zhilun, MA Jinpu, LI Congwei. The water level for prevention of up-floating under the condition of multi-level groundwater[J]. Geotechnical Engineering Technique, 2005, 19(4): 182-183, 217. (in Chinese)) |
| [11] |
黄志仑. 关于地下建筑物的地下水扬力问题分析[J]. 岩土工程技术, 2002(5): 273-274, 283. ( HUANG Zhilun. Analysis of ground water's uplift pressure on underground construction[J]. Geotechnical Engineering Technique, 2002(5): 273-274, 283. (in Chinese)) |
| [12] |
雷国平, 尹书冉, 黄召彪. 三峡工程蓄水后荆江河段设计水位的计算与确定[J]. 水运工程, 2014(12): 125-129. ( LEI Guoping, YIN Shuran, HUANG Zhaobiao. Calculation and determination of designed water stage at Jingjiang reach of the Yangtze River after impoundment of Three Gorges project[J]. Port & Waterway Engineering, 2014(12): 125-129. DOI:10.3969/j.issn.1002-4972.2014.12.025 (in Chinese)) |
| [13] |
CLAUDE-GOGUEN P E, LEED A P. NPCA buoyancy white paper[M]. National Precast Concrete Association, 2013.
|
| [14] |
董悦安, 王军辉, 王峰. 北京地区建筑工程抗浮设计水位不同计算方法对比研究[J]. 勘察科学技术, 2015(2): 5-8, 37. ( DONG Yue'an, WANG Junhui, WANG Feng. Comparative study on different calculation methods of design water level for anti floating in construction engineering in Beijing: taking the south district of kaiheng center project for example[J]. Site Investigation Science and Technology, 2015(2): 5-8, 37. (in Chinese)) |
| [15] |
李广信, 吴建敏. 浮力计算与粘土中的有效应力原理[J]. 岩土工程技术, 2003(2): 63-66. ( LI Guangxin, WU Jianmin. Calculation of uplift pressure on underground construction and effective stress principle in clay[J]. Geotechnical Engineering Technique, 2003(2): 63-66. (in Chinese)) |
| [16] |
张第轩, 陈龙珠. 地下结构抗浮计算方法试验研究[J]. 四川建筑科学研究, 2008, 34(3): 105-108. ( ZHANG Dixuan, CHEN Longzhu. Experimental on the computing method of anti-floating in underground structures[J]. Sichuan Building Science, 2008, 34(3): 105-108. (in Chinese)) |
| [17] |
李超. 建筑抗浮设计水位的合理取值[J]. 工程勘察, 2014, 42(4): 49-55. ( LI Chao. Reasonable value of water level for building anti-floating design[J]. Geotechnical Investigation & Surveying, 2014, 42(4): 49-55. (in Chinese)) |
| [18] |
熊欢. 地下结构抗浮设计中浮力的研究[D]. 长沙: 中南大学, 2013. (XIONG Huan. Research on bouyancy in anti-floating design underground structures[D]. Changsha: Central South University, 2013. (in Chinese)) http://cdmd.cnki.com.cn/Article/CDMD-10533-1014141462.htm
|
| [19] |
方玉树. 基于水压率讨论土中孔隙水压力及有关问题[J]. 岩土工程界, 2007, 10(5): 21-26. ( FANG Yushu. Discussion of pore water pressure in soil and the related problems based on water rate[J]. Geotechnical Engineering World, 2007, 10(5): 21-26. (in Chinese)) |
| [20] |
宋林辉, 梅国雄, 宰金珉. 黏土地基上基础抗浮模型试验研究[J]. 工程勘察, 2008(6): 26-30. ( SONG Linhui, MEI Guoxiong, ZAI Jinmei. Modal experimental study of foundation anti-float of clay foundation[J]. Geotechnical Investigation & Surveying, 2008(6): 26-30. (in Chinese)) |
| [21] |
崔岩, 崔京浩, 吴世红. 地下结构浮力模型试验研究[J]. 特种结构, 1999, 6(1): 32-35. ( CUI Yan, CUI Jinghao, WU Shihong. Modal experimental study of buoyancy of underground structures[J]. Special Structures, 1999, 6(1): 32-35. (in Chinese)) |
| [22] |
向科, 周顺华, 詹超. 浅埋地下结构静水浮力作用机理[J]. 同济大学学报(自然科学版), 2010, 33(3): 346-352, 357. ( XIANG Ke, ZHOU Shunhua, ZHAN Chao. Model test study of buoyancy on shallow underground structure[J]. Journal of Tongji University (Natural Science), 2010, 33(3): 346-352, 357. (in Chinese)) |
| [23] |
李广信. 土中水与孔隙水压力[J]. 广州大学学报(自然科学版), 2011(增刊1): 1-4. ( LI Guangxin. Water in the soil and the pore water pressure[J]. Journal of Guangzhou University (Natural Science), 2011(Suppl1): 1-4. (in Chinese)) |
| [24] |
介玉新, 温庆博, 李广信, 等. 有效应力原理几个问题探讨[J]. 煤炭学报, 2005, 30(4): 202-205. ( JIE Yuxin, WEN Qingbo, LI Guangxin, et al. Discussion of several issues about effective stress principle[J]. Journal of China Coal Society, 2005, 30(4): 202-205. (in Chinese)) |
| [25] |
倪春海, 宋林辉, 王宇豪, 等. 不同水压下的黏土孔压传递规律试验[J]. 南京工业大学学报(自然科学版), 2016, 38(1): 68-73, 82. ( NI Chunhai, SONG Linhui, WANG Yuhao, et al. Experimental study on pore pressure transmission law of clay under various water pressures[J]. Journal of Nanjing Tech University (Natural Science Edition), 2016, 38(1): 68-73, 82. (in Chinese)) |
| [26] |
蔡国成, 陶灵法, 吴炳华. 宁波平原地区地下建筑抗浮设防水位的探讨[J]. 科技通报, 2015, 31(7): 45-48. ( CAI Guocheng, TAO Lingfa, WU Binghua. Discussion about anti up-floating groundwater level of the underground buildings in Ningbo plain area[J]. Bulletin of Science and Technology, 2015, 31(7): 45-48. (in Chinese)) |
| [27] |
刘予, 孙颖, 殷琨. 南水北调引水进京后北京市地下水环境预测[J]. 水文地质工程地质, 2005, 32(5): 93-96. ( LIU Yu, SUN Ying, YIN Kun. Prediction of groundwater environment in Beijing after water entering the capital by the South-North Water Diversion[J]. Journal of Nanjing Tech University (Natural Science Edition), 2005, 32(5): 93-96. (in Chinese)) |
| [28] |
林文祺. 北京及其周边区域水资源联合调控初探[J]. 城市规划, 2005(6): 33-35, 75. ( LIN Wenqi. United control of water resource in the region of great Beijing[J]. City Planning Review, 2005(6): 33-35, 75. (in Chinese)) |
| [29] |
王军辉, 沈小克, 陶连金. 北京地区结构抗浮水位分析的区域法[J]. 工程勘察, 2015, 43(9): 43-50. ( WANG Junhui, SHEN Xiaoke, TAO Lianjin. Regional method to determine anti-buoyancy groundwater level in Beijing area[J]. Geotechnical Investigation & Surveying, 2015, 43(9): 43-50. (in Chinese)) |
| [30] |
安振东, 刘贯群, 张焘. 建筑物场区地下水位预测与抗浮水位确定——以青岛啤酒城改造为例[J]. 中国海洋大学学报, 2015, 45(4): 103-109. ( AN Zhendong, LIU Guanqun, ZHANG Tao, et al. The prediction of groundwater level about bui1ding area and determination of anti-floating water level:taking the transformation of Qingdao beer city for example[J]. Periodical of Ocean University of China, 2015, 45(4): 103-109. (in Chinese)) |
| [31] |
王玉洲, 李海坤, 苏志刚. 昆明市某项目事故水池抗浮设防水位研究[J]. 工程勘察, 2015, 43(7): 50-54. ( WANG Yuzhou, LI Haikun, SU Zhigang. Study on the anti-floating water level of a failed project in Kunming[J]. Geotechnical Investigation & Surveying, 2015, 43(7): 50-54. (in Chinese)) |
2. BGI Engineering Consultants Ltd., Beijing 100038, China
 2017
2017