长期处于环境水中的水坝、港口、水槽、桥梁等水利工程中的混凝土结构,钙溶蚀是最常见的病害之一[1-2]。软水侵蚀环境下,混凝土内部孔溶液中的钙离子在内外浓度梯度作用下,经扩散传输至外部环境水中,引起孔溶液中钙离子浓度的降低,骨架中的固体钙化物溶解,从而导致材料的孔隙率增加,进一步加大了材料的渗透性,加速了钙溶出过程,最终导致材料强度等力学性能下降[3]。
国内外学者在水泥基材料钙溶蚀方面做了大量研究工作,Gérard等[4]基于水泥净浆孔溶液中钙离子与固相产物之间的热动力学平衡关系建立了钙溶蚀模型,并利用已有试验数据验证了模型的合理性。Mainguy等[5]研究了水泥基材料溶蚀深度与钙溶蚀量之间的变化关系,根据固液钙之间的化学平衡关系,提出了以固相钙为传输控制参量的传输模型。Berner[6]利用水泥基材料钙溶蚀过程中固相钙溶解与液相钙扩散之间的平衡关系,给出了钙溶蚀过程中的固液平衡曲线。方坤河等[7-8]研究了混凝土的渗透溶蚀特性,并对渗透溶蚀过程中钙离子迁移过程进行了数值模拟。Wan等[9]建立了6 mol/L硝酸铵溶液加速溶蚀条件下水泥净浆的钙溶蚀模型,并利用试验测试结果对模型进行了分析和验证。材料内部孔溶液中钙离子在内外钙离子浓度梯度作用下经表层扩散至外部环境,因而表层离子交换条件对整个溶蚀进程影响很大,但相关研究中尚未涉及表层离子交换速率问题。本文基于Fick定律和质量守恒定律,利用水泥基材料中固体钙含量和孔溶液钙离子浓度之间的化学平衡关系,并考虑边界离子交换作用,建立了环境水侵蚀下水泥净浆的钙溶蚀模型,利用有限差分法对模型进行了数值求解,对模拟结果进行了试验验证,在此基础上对软水浸泡下的水泥净浆试件钙溶蚀过程进行了数值模拟。
1 模型建立 1.1 钙离子传输方程环境水中水泥净浆的钙溶蚀过程涉及固体钙的溶解和孔溶液中钙离子的扩散传输。由于静水条件下孔溶液中钙离子扩散速率远小于固体钙的溶解速率,本文忽略固体钙溶解对钙溶蚀进程的影响,认为孔溶液中钙离子浓度与CH (氢氧化钙)及CSH凝胶等固钙含量处于化学平衡状态,因此,静水条件下水泥净浆钙溶蚀进程主要由孔溶液中钙离子的扩散传输所控制。假定环境水中的水泥净浆处于饱水状态,根据Fick定律和质量守恒定律,且考虑边界上离子交换的Newton定律[10],可建立饱水条件下硬化水泥净浆中钙离子的一维传输方程:
| $ \left\{ \begin{array}{l} \frac{{\partial \left( {\varphi C + {C_{\rm{s}}}} \right)}}{{\partial t}} = \frac{\partial }{{\partial x}}\left[ {\varphi D\frac{{\partial C}}{{\partial x}}} \right]\\ 初始条件:C\left( {x,0} \right)\left| {_\mathit{\Omega }} \right. = {C_{{\rm{satu}}}}\\ 边界条件:{D_0}\frac{{\partial C}}{{\partial x}} = k\left( {C - {C_0}} \right)\left| {_\mathit{\Gamma }} \right. \end{array} \right. $ | (1) |
式中:φ为水泥净浆孔隙率;C为孔溶液中钙离子浓度(mol/m3);Cs为水泥净浆中固体钙含量(mol/m3);t为溶蚀时间(s);x为位置坐标(m);D为钙离子在水泥净浆中的有效扩散系数(m2/s),根据Garboczi和Bentz模型[11]:D =f(φ)D0,f(φ)为与材料微结构变化有关的函数[12],D0为钙离子在纯水中的扩散系数,25 ℃时,D0=5.0×10-10 m2/s;Csatu为孔溶液中钙离子初始饱和浓度(mol/m3);k为界面处钙离子传输速度(m/s);C0为环境水中钙离子浓度(mol/m3)。
相关研究[5, 13]表明,钙溶蚀过程中水泥净浆内固钙含量Cs与孔溶液中钙离子浓度C处于热力学平衡状态,并满足以下关系:
| $ {C_{\rm{s}}} = \left\{ \begin{array}{l} {C_{{\rm{CSH}}}}{\left( {\frac{C}{{{C_{{\rm{satu}}}}}}} \right)^{\frac{1}{3}}}\left( { - \frac{2}{{x_1^3}}{C^3} + \frac{3}{{x_1^2}}{C^2}} \right)\;\;\;\;\;0 \le C \le {x_1}\\ {C_{{\rm{CSH}}}}{\left( {\frac{C}{{{C_{{\rm{satu}}}}}}} \right)^{\frac{1}{3}}}\;\;\;\;{x_1} \le C \le {x_2}\\ {C_{{\rm{CSH}}}}{\left( {\frac{C}{{{C_{{\rm{satu}}}}}}} \right)^{\frac{1}{3}}} + \frac{{{C_{{\rm{CH}}}}}}{{{{\left( {{C_{{\rm{satu}}}} - {x_2}} \right)}^3}}}{\left( {C - {x_2}} \right)^3}\;\;\;{x_2} \le C \le {C_{{\rm{satu}}}} \end{array} \right. $ | (2) |
式中:CCSH,CCH分别为CSH凝胶相和氢氧化钙(CH)相含量(mol/m3);x1为CSH凝胶快速溶蚀时孔溶液中钙离子浓度(mol/m3);x2为CH完全溶解后CSH凝胶开始溶解时孔溶液中的钙离子浓度(mol/m3)。
根据钙溶蚀所引起的初始固体钙含量Cs0和溶蚀过程中的固体钙含量Cs之差,可建立溶蚀过程中水泥净浆孔隙率与固体钙溶蚀量之间的关系[9, 14]:
| $ \varphi = {\varphi _0} + {\mu _\rho }\left( {{C_{{\rm{s0}}}} - {C_{\rm{s}}}} \right) $ | (3) |
式中:φ0为初始孔隙率;μρ为固体钙的摩尔体积(mol/m3)。
1.2 数值求解式(1) ~(3) 为描述水环境下水泥净浆钙溶蚀过程的数学模型。为便于数值求解,将式(2) 和(3) 代入式(1),可得:
| $ \left[ {\varphi + \left( {1 - {\mu _{\rm{ \mathit{ ρ} }}}C} \right)\frac{{\partial {C_{\rm{s}}}}}{{\partial C}}} \right]\frac{{\partial C}}{{\partial t}} = \frac{\partial }{{\partial r}}\left[ {\varphi D\frac{{\partial C}}{{\partial r}}} \right] $ | (4) |
式(4) 是一维非线性非齐次的偏微分方程,为了提高该方程数值计算的精度和稳定性,采用三层隐式Crank-Nicolson格式[13]的有限差分法进行数值求解。
1.2.1 网格划分根据水泥净浆薄板在环境水中的溶蚀对称性,取试件厚度的一半进行网格划分,令试件厚度方向的空间步长为h,溶蚀过程中的时间步长取τ,则数值计算的空间等分M=0.5 L/h (L为板厚度)和溶蚀时间等分K=T/τ (T为总溶蚀时间),求解区域的空间和时间步采用下式描述:
| $ {x_j} = jh\left( {i = 1,2, \cdots ,j, \cdots ,M + 1} \right) $ | (5) |
| $ {t_k} = k\tau \left( {k = 1,2, \cdots ,k, \cdots ,K} \right) $ | (6) |
则点(xj,tk)处的钙离子浓度为Cjk。
1.2.2 差分格式令θ=∂Cs/∂C,则式(4) 中两项的差分格式如下:
| $ \left[ {\varphi + \left( {1 - {\mu _{\rm{ \mathit{ ρ} }}}C} \right)\theta } \right]\frac{{\partial C}}{{\partial t}} = \left[ {\varphi _j^k + \left( {1 - {\mu _{\rm{ \mathit{ ρ} }}}C_j^k} \right)\theta } \right]\frac{1}{{2\tau }}\left( {C_j^{k + 1} - C_j^{k - 1}} \right) $ | (7) |
| $ \frac{\partial }{{\partial x}}\left( {\varphi D\frac{{\partial C}}{{\partial x}}} \right) = \frac{1}{{2{h^2}}}\left[ {\left( {\varphi _{j + 1}^kD_{j + 1}^k + \varphi _j^kD_j^k} \right)\left( {C_{j + 1}^k - C_j^k} \right) -\\ \left( {\varphi _j^kD_j^k + \varphi _{j - 1}^kD_{j - 1}^k} \right)\left( {C_j^k - C_{j - 1}^k} \right)} \right] $ | (8) |
式(8) 中右端的Cnk(n=j-1, j, j+1) 在时间域上进行三层隐式差分:
| $ C_n^k = \frac{{C_n^{k + 1} + C_n^k + C_n^{k - 1}}}{3}\;\;\;\;\;\;\left( {n = j - 1,j,j + 1} \right) $ | (9) |
将式(7) ~(9) 代入式(4),并令:
| $ \mathit{\Psi }_j^k = \varphi _j^kD_j^k + \varphi _{j - 1}^kD_{j - 1}^k $ | (10) |
| $ \mathit{\Gamma }_j^k = \varphi _j^kD_j^k + \varphi _{j + 1}^kD_{j + 1}^k $ | (11) |
| $ \mathit{\Lambda }_j^k = \mathit{\Psi }_j^k + \mathit{\Gamma }_j^k + \frac{{3{h^2}}}{\tau }\left[ {\varphi _j^k + \left( {1 - {\mu _{\rm{ \mathit{ ρ} }}}C_j^k} \right)\theta } \right] $ | (12) |
| $ \mathit{\Theta }_j^k = \mathit{\Psi }_j^k + \mathit{\Gamma }_j^k - \frac{{3{h^2}}}{\tau }\left[ {\varphi _j^k + \left( {1 - {\mu _{\rm{ \mathit{ ρ} }}}C_j^k} \right)\theta } \right] $ | (13) |
| $ \mathit{\Omega }_j^k = \mathit{\Psi }_j^k + \mathit{\Gamma }_j^k $ | (14) |
因此,式(1) 的差分格式可表示为:
| $ \begin{array}{l} - \mathit{\Psi }_j^kC_{j - 1}^{k + 1} + \mathit{\Lambda }_j^kC_j^{k + 1} - \mathit{\Gamma }_j^kC_{j + 1}^{k + 1} = \mathit{\Psi }_j^kC_{j - 1}^k - \mathit{\Omega }_j^k\mathit{C}_j^k +\\ \mathit{\Gamma }_j^k\mathit{C}_{j - 1}^{k - 1} - \mathit{\Psi }_j^kC_{j - 1}^{k - 1} - \mathit{\Theta }_j^k\mathit{C}_j^{k - 1} + \mathit{\Gamma }_j^k\mathit{C}_{j + 1}^{k - 1}\\ \left( {j = 1,2, \cdots ,j, \cdots ,M + 1;k = 1,2, \cdots ,k, \cdots ,K} \right) \end{array} $ | (15) |
此外,式(1) 中边界条件表示为如下差分格式:
| $ {D_0}\frac{{C_2^k - C_0^k}}{{2h}} = {k_v}\left( {C_1^k - {C_0}} \right) $ | (16) |
根据式(15) 和(16),令β=2hkv/D0,可获得式(1) 的迭代方程为
| $ \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{C}}^{k + 1}} = \mathit{\boldsymbol{B}}{\mathit{\boldsymbol{C}}^k} + \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{C}}^{k - 1}} + \mathit{\boldsymbol{e}} $ | (17) |
式中,
| $ \mathit{\boldsymbol{A}} = \left[ {\begin{array}{*{20}{c}} {\mathit{\Lambda }_1^k + \beta \mathit{\Psi }_1^k}&{ - \left( {\mathit{\Gamma }_1^k + \mathit{\Psi }_1^k} \right)}&{}&{}&{}&{}&{}\\ { - \mathit{\Psi }_2^k}&{\mathit{\Lambda }_2^k}&{ - \mathit{\Gamma }_2^k}&{}&{}&{\left[ 0 \right]}&{}\\ {}& \ddots&\ddots&\ddots &{}&{}&{}\\ {}&{}&{ - \mathit{\Psi }_j^k}&{\mathit{\Lambda }_j^k}&{ - \mathit{\Gamma }_j^k}&{}&{}\\ {}&{}&{}& \ddots&\ddots&\ddots &{}\\ {}&{\left[ 0 \right]}&{}&{}&{ - \mathit{\Psi }_M^k}&{\mathit{\Lambda }_M^k}&{ - \mathit{\Gamma }_M^k}\\ {}&{}&{}&{}&{}&{ - \left( {\mathit{\Gamma }_{M + 1}^k + \mathit{\Psi }_{M + 1}^k} \right)}&{\mathit{\Lambda }_{M + 1}^k} \end{array}} \right] $ | (18) |
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{c}} { - \left( {\mathit{\Omega }_1^k + \beta \mathit{\Psi }_1^k} \right)}&{\mathit{\Gamma }_1^k + \mathit{\Psi }_1^k}&{}&{}&{}&{}&{}\\ {\mathit{\Psi }_2^k}&{ - \mathit{\Omega }_2^k}&{\mathit{\Gamma }_2^k}&{}&{}&{\left[ 0 \right]}&{}\\ {}& \ddots&\ddots&\ddots &{}&{}&{}\\ {}&{}&{\mathit{\Psi }_j^k}&{ - \mathit{\Omega }_j^k}&{\mathit{\Gamma }_j^k}&{}&{}\\ {}&{}&{}& \ddots&\ddots&\ddots &{}\\ {}&{\left[ 0 \right]}&{}&{}&{\mathit{\Psi }_M^k}&{ - \mathit{\Omega }_M^k}&{\mathit{\Gamma }_M^k}\\ {}&{}&{}&{}&{}&{\mathit{\Psi }_{M + 1}^k + \mathit{\Gamma }_{M + 1}^k}&{ - \mathit{\Omega }_{M + 1}^k} \end{array}} \right] $ | (19) |
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{c}} { - \left( {\mathit{\Theta }_1^k + \beta \mathit{\Psi }_1^k} \right)}&{\mathit{\Gamma }_1^k + \mathit{\Psi }_1^k}&{}&{}&{}&{}&{}\\ {\mathit{\Psi }_2^k}&{ - \mathit{\Theta }_2^k}&{\mathit{\Gamma }_2^k}&{}&{}&{\left[ 0 \right]}&{}\\ {}& \ddots&\ddots&\ddots &{}&{}&{}\\ {}&{}&{\mathit{\Psi }_j^k}&{ - \mathit{\Theta }_j^k}&{\mathit{\Gamma }_j^k}&{}&{}\\ {}&{}&{}& \ddots&\ddots&\ddots &{}\\ {}&{\left[ 0 \right]}&{}&{}&{\mathit{\Psi }_M^k}&{ - \mathit{\Theta }_M^k}&{\mathit{\Gamma }_M^k}\\ {}&{}&{}&{}&{}&{\mathit{\Psi }_{M + 1}^k + \mathit{\Gamma }_{M + 1}^k}&{ - \mathit{\Theta }_{M + 1}^k} \end{array}} \right] $ | (20) |
| $ \mathit{\boldsymbol{e}} = \left\{ {3\beta \mathit{\Psi }_1^k{C_0}0 \cdots 0 \cdots 0\;0} \right\} $ | (21) |
利用追赶法[15],可数值求解方程式(10),获得钙溶蚀过程中硬化水泥净浆中钙离子浓度C(x, t),再通过式(2) 和(3),可获得溶蚀过程中的固体钙浓度Cs(x, t)和孔隙率φ(x, t)。
2 模型验证由于水泥净浆的钙溶蚀过程非常缓慢,为了在较短时间内获得水泥净浆的钙溶蚀过程,以验证模型合理性,采用6 mol/L的氯化铵溶液[16],对不同水灰比的水泥净浆薄片进行加速溶蚀试验,测试薄片试件不同溶蚀时刻平均孔隙率和断面钙硅比,并与模型计算结果进行对比。
2.1 试验方法 2.1.1 原材料水泥采用P·O 52.5硅酸盐水泥,其中SiO2,Al2O3,Fe2O3,CaO,MgO,SO3所占百分比分别为21.10%,5.56%,3.98%,62.48%,1.76%和2.59%。氯化铵为化学分析纯试剂(AR),室温下溶解度为37.2 g/100 mL;拌合水采用自来水;氯化铵溶液采用去离子水配制。
2.1.2 试件制备及测试方法根据《普通混凝土拌合物性能试验方法标准》(GB/T 50080—2002),制备水灰比分别为0.35,0.45和0.55的水泥净浆试件,尺寸为10 mm×10 mm×2 mm。将制备的试件置于温度为(20±1) ℃、相对湿度大于95%的养护箱中养护28 d后,浸泡于盛有氯化铵溶液的水箱中,其氯化铵溶液浓度为6 mol/L,溶液体积为试件体积的100倍。
利用饱水干燥称重法[17],测试薄片试件的平均孔隙率。每次浸泡试验后,首先将试件在自来水下进行冲洗,再称量试件完全饱水时的质量ms;然后,运用高精度电子天平内置下挂式秤钩称取悬浮在蒸馏水中的样品质量mx;最后,将试件置于温度60 ℃的真空干燥箱中烘干至恒重,获得试件完全干燥时的质量md。根据式(22) 得到试件的平均孔隙率φ:
| $ \varphi = \left( {{m_{\rm{s}}} - {m_{\rm{d}}}} \right)/\left( {{m_{\rm{s}}} - {m_{\rm{x}}}} \right) \times 100\% $ | (22) |
利用电子扫描显微镜(SEM)及电子探针法,对不同溶蚀时间和水胶比的试件新鲜断面进行线扫描分析,并根据线扫描获得的各元素摩尔数,按式(23) 计算溶蚀过程中各试件断面钙硅比[18]:
| $ {R_{{\rm{sc}}}} = {n_{{\rm{Ca}}}}{M_{{\rm{Ca}}}}/\left( {{n_{{\rm{Si}}}}{M_{{\rm{Si}}}}} \right) $ | (23) |
式中: Rsc为钙和硅的质量比; nCa, nSi和MCa, MSi分别为钙、硅的摩尔数和相对原子质量。
2.2 模型验证及误差分析溶蚀试验采用的是6 mol/L氯化铵溶液加速溶蚀方法,模型中相关参数如表 1所示。
| 表 1 钙溶蚀模型中的相关参数 Table 1 Calculation parameters in a calcium leaching model |
孔隙率的试验值与模拟值对比如表 2所示,模型中按式(24) 计算薄片平均孔隙率:
| 表 2 水泥净浆试件孔隙率随溶蚀时间的变化 Table 2 Changes of porosity of cement paste specimen with leaching time |
| $ \overline {\varphi _{\rm{a}}^k} = \frac{1}{{M + 1}}\sum\limits_{j = 1}^{M + 1} {\varphi _j^k} $ | (24) |
式中:
由表 2可见,水泥净浆内孔隙率模拟值和实测值的误差均在10%以内,且溶蚀后期,孔隙率模拟值为定值。由于钙溶蚀过程中,水泥净浆孔隙率的增加主要由固体氢氧化钙(CH)的溶解引起[19],因此,计算机分析程序仅考虑了CH溶解产生的毛细孔对孔隙率的贡献。
2.2.2 钙硅比由于硬化水泥浆体溶解后生成的硅酸根离子含量低,硅的溶蚀程度也很低,因此,为方便计算,可忽略薄片中硅元素的变化。按式(25) 计算试件各时刻的平均钙硅比,钙硅比试验值与模拟值的结果对比如表 3所示。
| 表 3 水泥净浆试件钙硅比随溶蚀时间的变化 Table 3 Changes of Ca/Si of cement paste specimen with leaching time |
| $ {R_{{\rm{ak}}}} = \frac{1}{{{n_{\rm{s}}}\left( {M + 1} \right)}}\sum\limits_{j = 1}^{M + 1} {{S_{jk}}} $ | (25) |
式中:Rak为溶蚀k时刻试件的平均钙硅比;ns为硅元素初始浓度(mol/m3);Sjk为溶蚀k时刻第j层的固钙含量(mol/m3)。
从表 3可见,在溶蚀3 d时试验值和模拟值误差在8%以内,溶蚀15 d时误差在23%以内。后期误差相对较大的原因是,钙溶蚀过程中硅含量变化值虽然很小,但随着溶蚀时间的增加逐渐积累,而数值计算与分析时忽略了这一影响,因此钙硅比后期误差相对增大。综合表 2和3的结果可知,钙硅比、孔隙率的试验值和模拟值基本一致,说明所建钙溶蚀模型能较好地模拟硬化水泥净浆薄片的钙溶蚀过程。
3 数值算例 3.1 模型参数为弄清楚普通水环境下硬化水泥净浆的钙溶蚀规律,以置于纯净水中的水泥净浆薄板为例,分析环境水侵蚀下水泥净浆薄板的钙溶蚀过程。试件采用P·O 52.5硅酸盐水泥,矿物成分同2.1节原材料,模型中相关计算参数如表 1所示。
3.2 结果分析 3.2.1 钙离子浓度时空分布图 1给出了水泥净浆薄板在不同深度处孔溶液钙离子浓度随溶蚀发展的时空变化。

|
图 1 试件孔溶液中Ca2+浓度随时间和深度分布 Figure 1 Time-depth variation of calcium ion concentration in pore solution of specimen |
从图 1(a)可见,在薄片的不同深度处,钙离子浓度开始下降时对应的溶蚀时间不同;且薄片各深度处钙离子浓度的下降速率也有所不同,在薄板边界层(0.1 mm)及表层(1 mm),钙离子浓度在溶蚀前期下降尤为明显;在薄板3 mm (中间层),钙离子浓度开始下降后,其下降速率先降低后出现一个突增点,之后继续下降至趋于稳定,而在薄板5 mm (内层)深度处则呈现与3 mm深度(中间层)大致相同的规律,但其突增点较早出现且没有3 mm深度处的突增点明显。
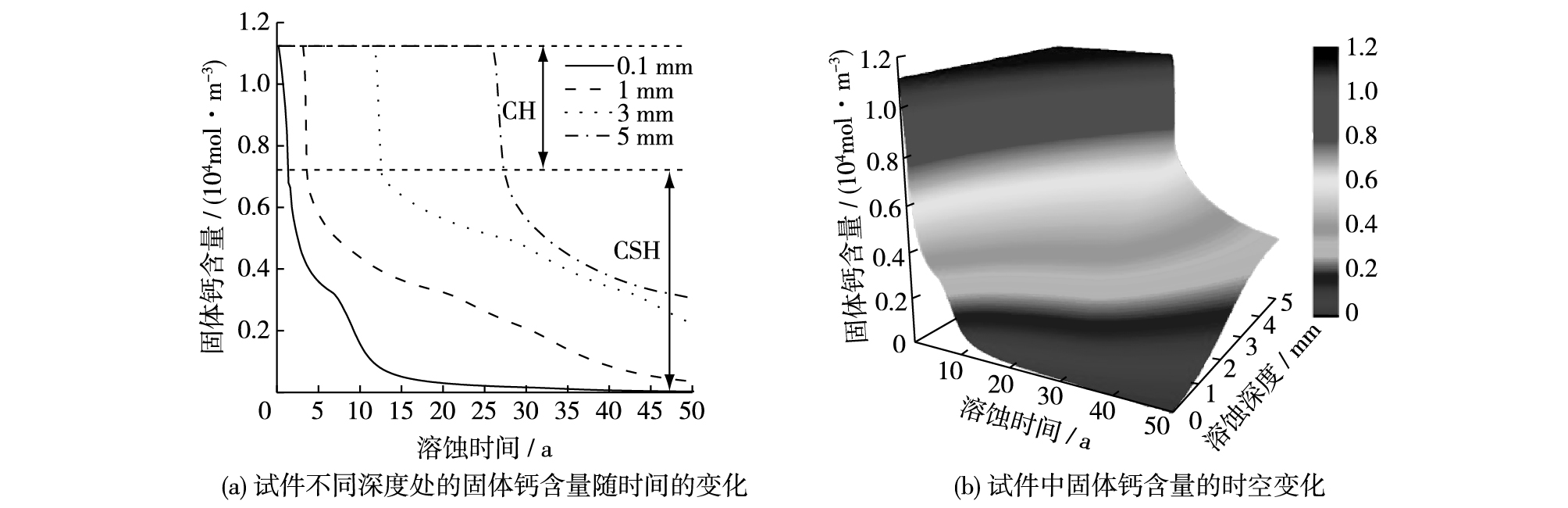
3.2.2 固体钙含量的变化规律CH和CSH凝胶是水泥的主要水化产物,对水泥浆体性能起着决定作用。为分析水环境下水泥净浆的钙溶蚀规律,图 2给出了薄板不同深度处CH和CSH凝胶含量随溶蚀时间的变化曲线。从图 2(a)可见,薄板各深度处CH含量随溶蚀时间的增加而减小,但不同深度处,CH从开始溶蚀至完全溶蚀对应的时间不同,薄板深度为0.1,1,3和5 mm处,完全溶蚀时间分别为420,208,653和936 d。从图 2(b)可见,CSH凝胶含量在不同深度处发生下降的时刻也不同,且初始下降速率较大,其后随着溶蚀时间的增加而减小;当溶蚀一定时间后,CSH凝胶含量的下降速率出现一个拐点,然后随溶蚀时间的增加而降低,并最终趋于稳定。这是因为,CSH凝胶可溶性远小于CH,CH溶蚀进程远快于CSH凝胶的溶解进程,且钙溶蚀是一个由表及里的溶解过程,因此,各深度处CSH凝胶的初始溶解时间各不相同。拐点则表示孔溶液中钙离子浓度已降低到了x1,此时CSH凝胶溶解速度较快,而随着CSH凝胶含量的减少,钙离子浓度也逐渐降低,最终将趋于0。图 3(a)给出了试件内固体钙(CH和CSH凝胶)含量随溶蚀时间的变化规律,由于固体钙含量是CH和CSH凝胶含量之和,其变化规律与图 2叠加后一致。图 3(b)给出了水泥净浆试件固体钙含量的时空变化规律。

|
图 2 试件不同深度处CH含量和CSH凝胶含量随时间的变化 Figure 2 Changes of CH and CSH content in specimen with leaching time |
|
图 3 水泥净浆试件中固体钙含量随溶蚀时间的变化 Figure 3 Time-depth variation of solid calcium content in cement paste specimen |
图 4给出了溶蚀过程中水泥净浆薄板试件在不同深度处的孔隙率随溶蚀时间的变化曲线。从图中可以看出,薄板截面各位置处孔隙率的初始增加速率很大,但相应的初始溶蚀时间不同,且深度越大,初始溶蚀时间越晚;在0.1 mm (边界层)深度处,溶蚀一定时间后出现1个明显拐点,后增加速率逐渐减小直至趋于稳定;在其他深度层,也呈现与边界层相似的规律,但随着深度的增加,拐点逐渐变得平缓。产生上述现象的原因是,水泥净浆薄板的钙溶蚀过程是由表及里进行的,深度越大,其开始溶蚀时间越长。溶蚀前期,由于CH的溶解速率较快,导致孔隙率增加也快,后期由于CSH凝胶的溶解速率相对较慢,故孔隙率的增加速率也较慢,当孔溶液中钙离子浓度达到了x2值,CSH凝胶溶解加快,导致孔隙率增加也较快。随着CSH凝胶含量的减小溶蚀速率逐渐变慢,孔隙率增加速率也变慢。因此,孔隙率变化主要与固体钙的溶蚀进程相关。

|
图 4 孔隙率随溶蚀时间的变化曲线 Figure 4 Changes of porosity in specimen with leaching time |
根据Fick定律和质量守恒定律,以及Newton边界条件,建立了环境水侵蚀下水泥净浆钙溶蚀计算模型,同时,开展了6M NH4Cl溶液中水泥净浆薄片的加速溶蚀试验,以验证模型的合理性,并利用该模型模拟了环境水侵蚀下水泥净浆薄板的钙溶蚀过程,结果表明:
(1) 模型计算值与试验值基本一致,所建立的钙溶蚀数值计算模型能较好地模拟软水环境下水泥净浆的钙溶蚀过程,可用于进一步分析水环境下因钙溶蚀引起的混凝土等水泥基材料耐久性退化问题。
(2) 钙溶蚀过程中,硬化水泥净浆的孔隙率变化主要与固体钙的溶蚀进程相关。在溶蚀前期,水泥净浆薄片中的固体钙含量下降速率及孔隙率增长速率较快;CH完全溶蚀后,水泥净浆固体钙溶蚀速率和孔隙率的增加速率逐渐减小。
| [1] |
孙伟. 现代结构混凝土耐久性评价与寿命预测[M]. 北京: 中国建筑工业出版社, 2015. ( SUN Wei. Durability evaluation and service life prediction of model concrete[M]. Beijing: China Architecture Building Press, 2015. (in Chinese))
|
| [2] |
邢林生, 聂广明. 混凝土坝坝体溶蚀病害及治理[J]. 水力发电, 2003, 29(11): 60-63. ( XING Linsheng, NIE Guangming. Corrosion and treatment of concrete dam body[J]. Hydroelectric Power, 2003, 29(11): 60-63. DOI:10.3969/j.issn.0559-9342.2003.11.019 (in Chinese)) |
| [3] |
CHOI Y, YANG E. Effect of calcium leaching on the pore structure, strength, and chloride penetration resistance in concrete specimens[J]. Nuclear Engineering and Design, 2013, 259: 126-136. DOI:10.1016/j.nucengdes.2013.02.049 |
| [4] |
GÉRARD B, BELLEGO C, BERNARD O. Simplified modelling of calcium leaching of concrete in various environments[J]. Materials & Structures, 2002, 35(10): 632-640. |
| [5] |
MAINGUY M, TOGNAZZI C, TORRENTI J M, et al. Modelling of leaching in pure cement paste and mortar[J]. Cement & Concrete Research, 2000, 30(1): 83-90. |
| [6] |
BERNER U. Evolution of pore water chemistry during degradation of cement in a radioactive waste repository environment[J]. Waste Management, 1992, 12(2): 201-219. |
| [7] |
方坤河, 阮燕, 吴玲, 等. 混凝土的渗透溶蚀特性研究[J]. 水力发电学报, 2001(1): 31-39. ( FANG Kunhe, RUAN Yan, WU Ling. A study of leakage dissolution characteristic of concrete[J]. Journal of Hydroelectric Engineering, 2001(1): 31-39. (in Chinese)) |
| [8] |
李新宇, 方坤河. 软水溶蚀作用下水工碾压混凝土渗透特性研究[J]. 长江科学院院报, 2008, 25(4): 81-84. ( LI Xinyu, FANG Kunhe. Permeability of hydraulic roller compacted concrete under soft water[J]. Journal of Yangtze River Scientific Research Institute, 2008, 25(4): 81-84. (in Chinese)) |
| [9] |
WAN K, LI Y, SUN W. Experimental and modelling research of the accelerated calcium leaching of cement paste in ammonium nitrate solution[J]. Construction and Building Materials, 2013, 40(3): 832-846. |
| [10] |
MAEKAWA K, ISHIDA T, KISHI T. Multi-scale modeling of structural concrete[M]. London: Spon Press, 2009.
|
| [11] |
GARBOCZI E, BENTZ D. Computer simulation of the diffusivity of cement-based materials[J]. Journal of Materials Science, 1992, 27(8): 2083-2092. DOI:10.1007/BF01117921 |
| [12] |
BEJAOUI S, BARY B. Modeling of the link between microstructure and effective diffusivity of cement pastes using a simplified composite model[J]. Cement and Concrete Research, 2007, 37(3): 469-480. DOI:10.1016/j.cemconres.2006.06.004 |
| [13] |
NAKARAI K, ISHIDA T, MAEKAWA K. Modeling of calcium leaching from cement hydrates coupled with micro-pore formation[J]. Journal of Advanced Concrete Technology, 2006, 4(3): 395-407. DOI:10.3151/jact.4.395 |
| [14] |
余健, 左晓宝, 汤玉娟. 软水环境下砂浆钙溶蚀过程及孔隙率变化分析[J]. 南京理工大学学报, 2016, 40(3): 366-373. ( YU Jian, ZUO Xiaobao, TANG Yujuan. Analysis of calcium leaching process and porosity change of mortar under environment of soft water[J]. Journal of Nanjing University of Science and Technology, 2016, 40(3): 366-373. (in Chinese)) |
| [15] |
徐树方, 高立, 张平文. 数值线性代数[M]. 北京: 北京大学出版社, 2000. ( XUN Shufang, GAO Li, ZHANG Pingwen. Numerical linear algebra[M]. Beijing: Beijing University Press, 2000. (in Chinese))
|
| [16] |
YANG H, JIANG L, ZHANG Y, et al. Predicting the calcium leaching behavior of cement pastes in aggressive environments[J]. Construction and Building Materials, 2012, 29(4): 88-96. |
| [17] |
CPC R. Absorption of water by immersion under vacuum[J]. Materials & Structures, 1984, 17(5): 391-394. |
| [18] |
WAN K, LI L, SUN W. Solid-liquid equilibrium curve of calcium in 6 mol/L ammonium nitrate solution[J]. Cement and Concrete Research, 2013, 53(11): 44-50. |
| [19] |
JAINT J, NEITHALATH N. Physico-chemical changes in nano-silica and silica fume modified cement paste in response to leaching[J]. International Journal of Materials & Structural Integrity, 2009, 3(2): 114-133. |
 2017
2017 
