混凝土作为一种多孔介质材料,内部存在大量微观孔隙和微裂纹。桥墩和大坝等混凝土建筑物,由于长期处于水环境中,水渗入混凝土内部孔隙中,由此产生内部孔隙水压,其中高孔隙水压会使混凝土内的微观裂纹逐渐扩展、微裂纹之间的贯通最终会形成宏观裂纹,导致混凝土的材料性能劣化,从而影响混凝土的整体性能。
国内外众多学者对在水环境下混凝土动、静态性能的研究已取得了丰硕成果。Butler[1]通过试验研究发现主动孔隙水压力使材料产生拉应变。Cadoni等[2]分析了不同饱和度对混凝土应变速率的影响。Yaman等[3]发现随着孔隙率和孔隙中含水量的增加,混凝土的强度降低,弹性模量增大。王海龙等[4]建立了饱和混凝土在静态荷载作用下的本构模型。杜修力等[5]研究了不同饱和度混凝土的峰值拉应变随孔隙率的变化。李宗利等[6]发现随着孔隙水压的增加,混凝土的抗压强度、弹性模量都呈现逐渐降低的规律。张永亮等[7]通过试验发现当应变率大于某个临界值时, 饱和混凝土的动态强度大于干燥混凝土的动态强度。彭刚等[8]分析认为围压的存在提高了混凝土的率敏感性;混凝土损伤特性在峰前服从Weibull统计分布,峰后服从Lognormal统计分布。刘博文等[9]通过试验发现随着孔隙水压循环次数的增加,峰值应力呈现先增后减的变化趋势。黄常玲等[10]分析了孔隙水压力和当前孔隙率对饱和混凝土微裂纹的演化过程。最新研究结果表明,孔隙水压力的存在改变了混凝土材料应力达到峰值时所对应的抗压强度,与干燥混凝土相比,准静态饱和混凝土在各种应力状态下的抗压强度均有所降低[11]。
目前,国内外对混凝土在水环境中受孔隙水压作用下率效应的研究相对较少,尤其是初始孔隙水压对混凝土在动、静荷载作用下的研究还不够充分。本文进行了干燥无水压和不同孔隙水压(0,2,5和10 MPa)下饱和混凝土在不同应变速率(10-5/s,10-4/s,10-3/s,10-2/s)下的混凝土压缩试验,取10-5/s为准静态应变速率,每种速率下保证3组有效试验数据以确保数据完整性。
1 试验设计 1.1 试件制备及养护试验采用Φ300 mm×600 mm的圆柱体,所用水泥为宜昌三峡水泥有限公司生产的P·O 42.5普通硅酸盐水泥,其3 d和28 d的抗压和抗折强度均满足规范要求。制备混凝土试件的材料用量为:水泥370 kg/m3,粗骨料1 199 kg/m3,细骨料646 kg/m3,水185 kg/m3。将浇筑试件置于标准养护条件下养护28 d,然后自然养护至试验开始。
1.2 试验设备力学试验采用三峡大学与长春朝阳试验仪器有限公司联合研制的10 MN大型多功能液压伺服静动力三轴仪。静动态循环加卸载试验采用等应变增量控制,并由电脑系统全程控制;利用加压阀系统给围压桶注水,对混凝土试件进行加压处理,最大围压和最大孔隙水压值均为30 MPa。为了对试件变形进行准确测量,围压桶中还配备了高压水环境内试件变形测量装置。同时围压桶内配备VWP型振弦式渗压计,渗流计埋设在混凝土试件内部,可有效测量混凝土结构内部渗透(孔隙)水压力。
2 试验过程试验中混凝土试样不隔水密封,与围压水直接接触,试验共分为两部分:不同围压水作用下混凝土孔隙水压变化规律试验和不同初始孔隙水压力下混凝土动态力学特性试验。
2.1 围压水与孔隙水压变化规律试验(1) 制样:将渗压计沿混凝土高度方向竖直埋入其内部,且浇筑前对渗压计透水部件前端采用细砂和土工布进行包裹,同时将VWP型振弦式渗压计与围压设备连接口进行封硅胶处理,安装试件,密封围压桶,注水至围压桶全部充满水。整个过程需对VWP型振弦式渗压计所显示的读数进行记录,观察并记录混凝土内部孔隙水压变化。
(2) 施加孔隙水压:采用位移加载方式给混凝土试件施加围压,待围压接近设定压力时改控制方式为围压控制。整个过程中需对VWP型振弦式渗压计所显示的读数进行实时记录,待围压和VWP型振弦式渗压计显示的读数均保持稳定且相等时,改变围压至预设值,同步记录渗压计读数。直到孔隙水压值与围压值达到一致。
(3) 重复步骤(2),直至整个试验完成。试验完成后,将围压卸载至0后排水,待围压桶内水排净后,关闭油泵并将仪器复位。
2.2 不同初始孔隙水压力下混凝土动态力学特性试验(1) 试验前准备:安装试件,密封围压桶,对内注水至围压桶全部充满水;连接EDC驱动程序,以围位移控制方式通过加压阀给试件施加围压,待接近所设围压值时转换控制方式,以围压进行控制,达到所设围压值后保持恒压16~17 h,此时,围压和围位移保持不变,可认为混凝土已达饱和状态。
(2) 正式加载:进行应变速率为10-5/s和10-4/s的试验时,选用辅助伺服油源,进行应变速率为10-3/s和10-2/s的试验时,选用主伺服油源;给试件预加20 N的初始静荷载,然后以位移控制方式,按设定的应变速率对试件进行加载直至试件破坏,加载过程中保证围压恒定不变。
(3) 卸载及后续处理:试验完成后,将围压卸载至0后排水,待围压桶内水排净后,关闭油泵并将仪器复位,对破坏后的混凝土试样拍照并清理试件残渣。
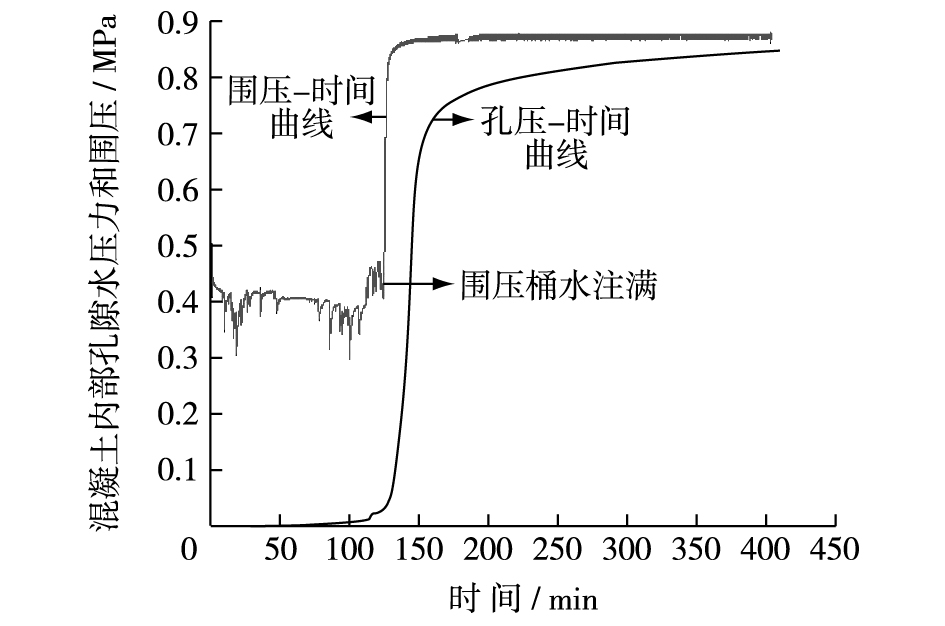
3 试验结果分析 3.1 孔隙水压与围压规律分析依据试验所得到围压和孔隙水压随时间变化的数据,对其进行处理、分析和汇总得到围压桶内注水至混凝土达到饱和阶段中围压和孔隙水压随时间变化的曲线,见图 1。
|
图 1 围压和孔压随时间变化曲线 Figure 1 Confining pressure and pore pressure curve changes with time |
由图 1可知,当围压达到预设值0.875 MPa时,孔隙水压并未完全达到围压值,而是略小于围压值。混凝土内部孔隙水压力从快速增长到缓慢增长至趋于稳定所需时间大约为540 min,即历经9 h混凝土内部孔隙水压才能最终达到与施加围压相等的值。由试验全过程可知,混凝土内部孔隙已经充满围压水,与外部围压已经连通而成为一个整体,因此通过改变围压值得到相对应初始孔隙水压的方法合理可行。
3.2 峰值应力分析采用施加预设围压的方式对混凝土进行水气饱和,混凝土内部具有与围压一致的初始孔隙水压力。混凝土在4种不同应变速率下(10-5/s,10-4/s,10-3/s,10-2/s)的峰值应力见表 1。
| 表 1 不同初始孔隙水压下混凝土峰值应力 Table 1 Peak stress values of concrete under different initial pore water pressures |
由表 1可知,饱和混凝土(初始孔隙水压为0) 比干燥混凝土在各种应力状态下的抗压强度均有所下降,这与文献[7, 11]的观点基本一致,说明孔隙水的存在削弱了混凝土颗粒间的作用,在压力作用下促使更多的细微裂纹发展,从而降低了材料强度。当初始孔隙水压逐渐增大时,在不同应变速率下不同初始孔隙水压混凝土的抗压强度均大于干燥混凝土,当初始孔隙水压较小时,在不同的应变速率下混凝土内部裂隙并不能被孔隙水完全填满,此时混凝土内部的Stefan效应并不明显,但是当初始孔隙水压逐渐增大后,由于孔隙水能够在初始孔隙水压作用下填满裂隙,此时混凝土的Stefan效应更加充分,因此饱和混凝土的抗压强度均比干燥混凝土有所提高。
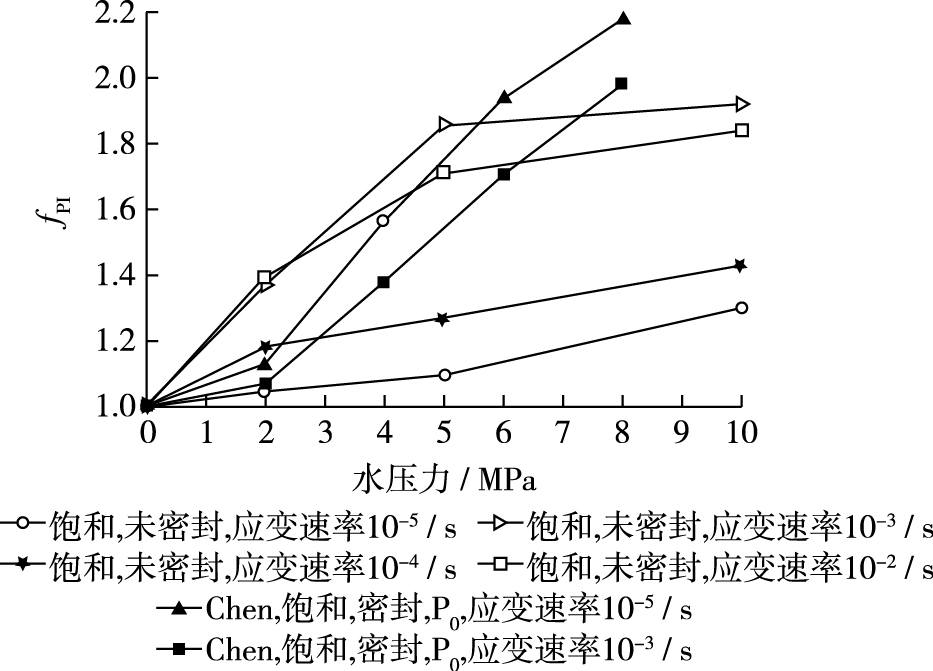
结合陈樟福生等[12]研究成果,可以得到密封与不密封饱和混凝土有初始孔隙水压和无初始孔隙水压力下的峰值应力变化(见图 2)。定义孔隙水压力对混凝土峰值应力增强因子(fPI)为不同初始孔隙水压力下与孔隙水压力为0时,混凝土峰值应力的比值,即fPI=σpkp/αpko。
|
图 2 不同水压下密封与不密封饱和混凝土fPI Figure 2 fPI of sealed and non-sealed saturated concrete under different water pressures |
在高应变速率(10-3/s)下,文献[12]由于对混凝土进行了密封,隔绝了外界围压与混凝土内部裂纹的连通,使得其内部孔隙水压力只能由饱和混凝土内部孔隙水产生。高应变速率下,内部孔隙水压力会增大,在一定程度上能够抵消外界围压的作用,最终导致其fPI值小于本文的值。相对于密封状态的饱和混凝土,有初始孔隙水压2 MPa饱和混凝土的fPI值提高了28.46%,且随着水压力的增加,两者相差幅度呈逐渐减小趋势,由于初始孔隙水压的存在,在高应变速率下,混凝土内部裂纹扩展与围压水形成贯通孔隙水压,从而增强了孔隙水压力对混凝土峰值应力的增益效果,随着初始孔隙水压力的增大,其增强效果逐渐减弱,初始孔隙水压力对混凝土的劣化效果逐渐明显。由于高孔隙水压力对混凝土强度增强作用很大部分需抵消其对混凝土强度劣化作用,使得孔隙水压力对混凝土强度增强作用下降。
本研究和文献[12]虽然都进行了不密封饱和混凝土在围压下的动态压缩试验,但是混凝土fPI值有很大差别,这是因为文献[12]通过采用自然饱和方式对混凝土进行饱和,然后开展围压(0, 2, 4, 6和8 MPa)下不密封饱和混凝土的动态受压试验。本研究采用施加预设围压的方式对混凝土进行饱和,混凝土内部具有与围压一致的初始孔隙水压力,而文献[12]试验中混凝土内部初始孔隙水压力很小,可近似为0 MPa。正是由于混凝土内部初始孔隙水压的存在,使得两者试验结果呈现较大差别。
由图 3知,在低应变速率(10-5/s)下,低孔隙水压下(0~6 MPa)的试验结果与文献[12]fPI值相差不大,表明静态加载过程中,围压与混凝土内部孔隙贯通形成贯通孔隙水压力,其值等于围压值,围压与内部孔隙水压力的作用相互抵消,从而使得两者fPI相差不大,这同时也说明采取的利用加围压施加孔隙水压的方式其初始损伤很小,也验证了这个方法的可靠性。但当初始孔隙水压达到8 MPa时,饱和混凝土比高孔隙水压混凝土fPI值提高了17.8%,且具有逐渐增大趋势,这是由于混凝土内部的高孔隙水压受静态加载影响,内部孔隙水逐步进入裂隙尖端,形成“超孔隙水压”促使裂缝扩展延伸,最终导致试件完全破坏。

|
图 3 不同水压下不同处理饱和混凝土fPI Figure 3 fPI of different saturated concrete under different water pressures |
在高应变速率(10-3/s)下,水压力为2 MPa时,相对于文献[12]的0 MPa孔隙水压力的fPI提高了71.57%,说明有初始孔隙水压的混凝土可以更早地将试件内部裂缝填满孔隙水,提高了孔隙水对混凝土增益的效果。随着水压力增加,两者之间的差别呈现减小趋势,表明高应变速率过程中,当混凝土内部初始孔隙水压为0 MPa时,由于试验过程中混凝土内部裂纹会扩展,围压水通过裂缝逐渐渗透进入混凝土内部形成孔隙水压,在高应变速率下,混凝土内部孔隙水压值大于围压,因此在破坏过程中围压水不会进入裂缝尖端,不能形成“楔入作用”,同时高应变速率提高了孔隙水压力对混凝土的增强效果,从而使得混凝土fPI值增大。
由表 1计算得到定应变速率下,相对于初始孔隙水压0 MPa时,不同初始孔隙水压下混凝土峰值应力的变化率,见表 2。
| 表 2 不同初始孔隙水压下混凝土峰值应力变化率 Table 2 Change rates of peak stress of concrete under different initial pore water pressures |
由表 2可见,高应变速率下,混凝土峰值应力的变化率随初始孔隙水压增加整体上呈现逐渐增大趋势,且增大的速率和幅度远大于低应变速率下的变化率。分析表明,应变速率在很大程度上提高了初始孔隙水压作用对混凝土峰值应力的增益效果,应变速率越高,初始孔隙水压力对混凝土峰值应力增强的效果越明显,这是由于当应变速率越高且初始孔隙水压较小时,孔隙水不容易达到裂隙尖端,但是初始孔隙水压增至一定数值可以使孔隙水瞬间填满裂隙尖端,此时混凝土的Stefan效应得到加强,因此应变速率越高,初始孔隙水压力对混凝土峰值应力增强的效果越明显。
3.3 峰值应力的率敏感性分析由表 2计算得到定孔隙水压,相对于准静态应变速率(10-5/s)时,不同应变速率下混凝土峰值应力变化率见表 3。
| 表 3 不同应变速率下混凝土峰值应力变化率 Table 3 Change rates of peak stress of concrete under different strain rates |
定初始孔隙水压下,随着应变速率的提高,混凝土峰值应力的变化率逐渐增大。应变速率较低(10-4/s)时,随孔隙水压增加,混凝土峰值应力的变化率并无明显变化;在高应变速率下,不同应变速率时,混凝土峰值应力变化率呈现明显差别,且均有了很大程度的提高。分析表明,初始孔隙水压力在较大程度上提高了混凝土峰值应力的率敏感性。
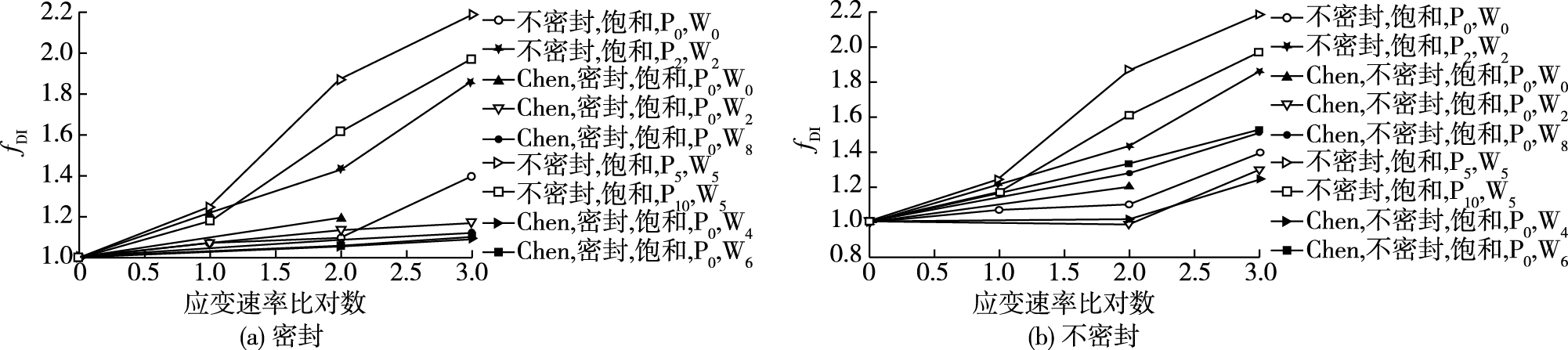
结合文献[12]研究成果,得到不同初始孔隙水压下饱和混凝土峰值应力变化,见图 4(a)。定义混凝土动态强度增强因子(fDI)为混凝土峰值应力与准静态应变速率下的比值,即fDI=1+log(
|
图 4 不同应变速率下混凝土动态强度增强因子 Figure 4 Dynamic factor of concrete under different strain rates |
初始孔隙水压力在一定程度上提高了混凝土峰值应力的率敏感性。在初始孔隙水压力为10 MPa时,其峰值应力的率敏感性出现一定幅度的降低,表明高初始孔隙水压下,应变速率在提高混凝土峰值应力以及提高孔隙水压对峰值应力的增益作用的同时,更大程度上提高了孔隙水压对混凝土强度的劣化作用,从而导致混凝土峰值应力率敏感性能的降低。文献[12]因为对混凝土进行了密封,使得在不同水压下,混凝土峰值应力的提高小于本研究的提高值,表明孔隙水压力对混凝土峰值应力率敏感性的提高效果要强于围压水对混凝土峰值应力率敏感性的提高效果。由图 4(b)知,不同水压力下,本研究fDI整体上比文献[12]的提高很多。在水压力为2 MPa时,不同应变速率下(10-3/s和10-2/s),相对于文献[12]的成果,本研究的fDI值分别提高了44.88%和43.83%。文献[11]在水压力为2和4 MPa下的fDI值相对于0 MPa反而出现降低现象,而在水压力为6和8 MPa时,其fDI值大于0 MPa的fDI值,这是由于高孔隙水压增强了应变速率对混凝土峰值应力增强效果。
本研究中不同水压下,混凝土强度增强因子随着应变速率的变化逐渐增加,由于初始孔隙水压的存在,外界围压对混凝土破坏作用并不能起到促进作用,其会与混凝土内部孔隙形成贯通孔隙水压,从而使得在不同应变速率下,混凝土fDI整体逐步增强。
4 混凝土损伤本构模型众多研究者认为混凝土力学特性服从Weibull统计分布。王春来等[13]采用Weibull统计概率密度函数来描述应力-应变全曲线, 此本构模型能够较好描述试验结果。梁辉等[14-15]基于Weibull统计和Lognormal统计分布理论,构建出混凝土材料分段式率型单轴受压损伤本构模型;在峰值应变之后,随着应变增加,由本构方程密度函数对峰值应变后混凝土的应力-应变曲线进行修正。下降段应力-应变全曲线方程为:
| $ \sigma = a\exp \left( { - 0.5{{\left( {\ln \left( {\varepsilon /b} \right)/t} \right)}^2}} \right) $ | (1) |
由应力-应变全曲线的几何特征,可以得到边界条件① 当ε=εpk时,dσ/dε=0;② 当ε=εpk时,σ=σpk。
将边界条件② 代入式(1) 得:
| $ a = {\sigma _{{\rm{pk}}}} $ | (2) |
将式(1) 对ε求导,得:
| $ {\rm{d}}\sigma /{\rm{d}}\varepsilon = - a\ln \left( {\varepsilon /b} \right)/\left( {{t^2}\varepsilon } \right)\exp \left( { - 0.5{{\left( {\ln \left( {\varepsilon /b} \right)/t} \right)}^2}} \right) $ | (3) |
代入边界条件得:
| $ b = {\sigma _{{\rm{pk}}}} $ | (4) |
由此得到混凝土下降段应力-应变全曲线方程为:
| $ \sigma = {\sigma _{{\rm{pk}}}}\exp \left( { - 0.5{{\left( {\ln \left( {\varepsilon /{\varepsilon _{{\rm{pk}}}}} \right)/t} \right)}^2}} \right) $ | (5) |
式中:E,σpk和εpk为弹性模量、峰值应力和峰值应变;t为下降段形状参数,需要通过对应力-应变全曲线拟合后得到。从而可以得到混凝土分段式本构方程为:
| $ \sigma = \left\{ \begin{array}{l} {E_0}\varepsilon \exp \left( { - \frac{1}{m}{{\left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)}^m}} \right)\;\;\;\;\;\;\;0 \le \varepsilon \le {\varepsilon _{{\rm{pk}}}}\\ {\sigma _{{\rm{pk}}}}\exp \left( { - \frac{1}{2}{{\left( {\frac{{\ln \left( {\varepsilon /{\varepsilon _{{\rm{pk}}}}} \right)}}{t}} \right)}^2}} \right)\;\;\;\;\;\varepsilon \ge {\varepsilon _{{\rm{pk}}}} \end{array} \right. $ | (6) |
式中:m=1/ln(E0εpk/σpk),m为上升段曲线参数,E0为初始弹性模量。
文献资料[13, 16]表明,混凝土峰值应变随应变速率的变化不太明显,随着应变速率增加,其变化波动比较大;峰值应力和初始弹性模量随应变速率变化关系,可采用直线方程表示。由此,对初始弹性模量E0和峰值应力σpk引入应变速率,分别构建其与应变速率的函数关系,记为
| $ {E_0}\left( {\dot \varepsilon } \right) = {E_{{\rm{s}}0}}\left( {1 + \alpha \log \left( {{{\dot \varepsilon }_{\rm{d}}}/{{\dot \varepsilon }_{\rm{s}}}} \right)} \right) $ | (7) |
| $ {\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right) = {\sigma _{{\rm{pks}}}}\left( {1 + \beta \log \left( {{{\dot \varepsilon }_{\rm{d}}}/{{\dot \varepsilon }_{\rm{s}}}} \right)} \right) $ | (8) |
式中:
| $ m\left( {\dot \varepsilon } \right) = 1/\left( {\ln \left( {{E_0}\left( {\dot \varepsilon } \right){\varepsilon _{{\rm{pk}}}}/{\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)} \right)} \right) $ | (9) |
损伤变量是用来描述材料在破坏过程中连续性破坏程度或材料劣化程度的变量。在各向同性损伤条件下,混凝土材料的本构关系可以通过无损材料中的名义应力表示:
| $ \varepsilon = \sigma /{{\tilde E}_0} = \tilde \sigma /{E_0} = \sigma /\left( {\left( {1 - D} \right){E_0}} \right) $ | (10) |
将式(7) ~(9) 代入式(6) 中,得到基于Weibull统计分布理论,考虑率效应的混凝土损伤本构方程:
| $ \sigma = \left\{ \begin{array}{l} {E_0}\left( {\dot \varepsilon } \right)\varepsilon \exp \left( {\ln \left( {\frac{{{\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)}}{{{E_0}\left( {\dot \varepsilon } \right){\varepsilon _{{\rm{pk}}}}}}} \right){{\left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)}^{\frac{1}{{\ln \left( {{E_0}\left( {\dot \varepsilon } \right){\varepsilon _{{\rm{pk}}}}/{\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)} \right)}}}}} \right)\;\;\;\;\;\;\;0 \le \varepsilon \le {\varepsilon _{{\rm{pk}}}}\\ {\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)\exp \left( { - \frac{1}{2}{{\left( {\frac{{\ln \left( {\varepsilon /{\varepsilon _{{\rm{pk}}}}} \right)}}{t}} \right)}^2}} \right)\;\;\;\;\;\;\;\;\;\varepsilon \ge {\varepsilon _{{\rm{pk}}}} \end{array} \right. $ | (11) |
将式(7), (8) 和(11) 代入(10) 得到损伤变量:
| $ D = \left\{ \begin{array}{l} 1 - \exp \left( {\ln \left( {\frac{{{\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)}}{{{E_0}\left( {\dot \varepsilon } \right){\varepsilon _{{\rm{pk}}}}}}} \right){{\left( {\frac{\varepsilon }{{{\varepsilon _{{\rm{pk}}}}}}} \right)}^{\frac{1}{{\ln \left( {{E_0}\left( {\dot \varepsilon } \right){\varepsilon _{{\rm{pk}}}}/{\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)} \right)}}}}} \right)\;\;\;\;\;\;\;0 \le \varepsilon \le {\varepsilon _{{\rm{pk}}}}\\ 1 - {\sigma _{{\rm{pk}}}}\left( {\dot \varepsilon } \right)\exp \left( { - \frac{1}{2}{{\left( {\frac{{\ln \left( {\varepsilon /{\varepsilon _{{\rm{pk}}}}} \right)}}{t}} \right)}^2}} \right)/\left( {{E_0}\left( {\dot \varepsilon } \right)\varepsilon } \right)\;\;\;\;\;\;\;\varepsilon \ge {\varepsilon _{{\rm{pk}}}} \end{array} \right. $ | (12) |
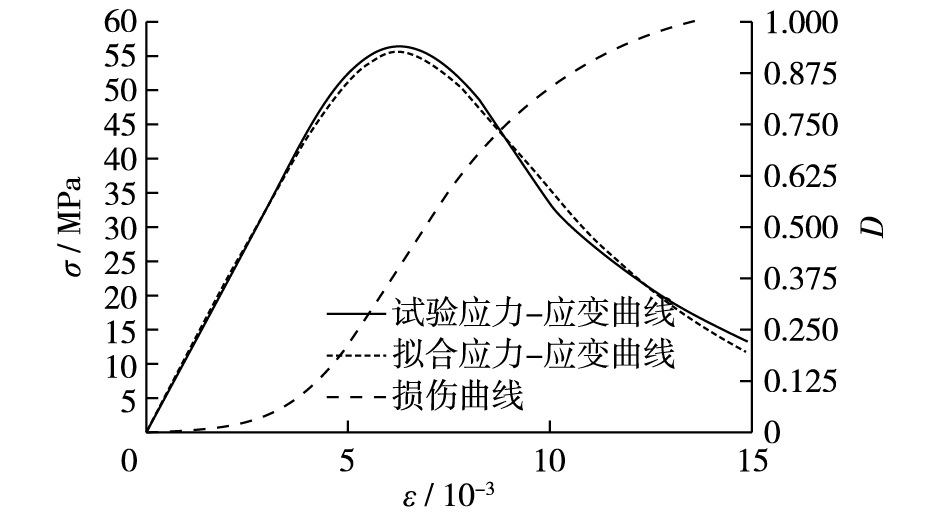
利用式(12) 对加载速率10-2/s下的初始孔隙水压为5 MPa的混凝土试件进行拟合分析,结果见图 5。不同初始孔隙水压作用下,各应变速率下的混凝土应力应变全曲线拟合相关系数均在0.97以上,采用本文所建立的率型损伤本构模型对不同孔隙水压作用下,不同应变速率下混凝土常三轴压缩试验数据进行拟合,结果良好。由此表明:本研究所建模型,可以用来描述不同初始孔隙水压力和不同应变速率下,混凝土应力-应变全曲线及损伤变化规律。
|
图 5 初始孔隙水压力5 MPa与应变速率10-2/s全曲线拟合分析 Figure 5 Whole curve fitting analysis of initial pore water pressure 5 MPa and loading rate 10-2s-1 |
不同围压下,混凝土内部孔隙水压呈现出先迅速增大后逐渐缓慢递增直至稳定,所需时间为9 h。不同应变速率下,混凝土峰值应力随初始孔隙水压的增大逐渐增大,高应变速率提高了初始孔隙水压力对混凝土峰值应力的影响;初始孔隙水压力在较大程度上提高了混凝土峰值应力的率敏感性。在准静态应变速率下,初始孔隙水压作用与围压作用发生相互抵消;在高应变速率下,高初始孔隙水压力对混凝土强度增强效果下降。
基于Weibull和Lognormal统计分布理论,以及Lemaitre应变等效原理,构建了混凝土率型损伤本构模型。采用建立的率型损伤本构模型对不同初始孔隙水压下,混凝土常三轴压缩应力-应变曲线进行了统计验证,所得拟合效果良好,所建模型可以用来描述不同工况下,混凝土应力-应变全曲线及损伤变化规律。
| [1] |
BUTLER J E. The influence of pore pressure upon concrete[J]. Magazine of Concrete Research, 1981, 33(114): 3-17. DOI:10.1680/macr.1981.33.114.3 |
| [2] |
CADONI E, LABIBES K, ALBERTINI C, et al. Strain-rate effect on the tensile behaviour of concrete at different relative humidity levels[J]. Materials and Structures, 2001, 34(1): 21-26. DOI:10.1007/BF02482196 |
| [3] |
YAMAN I O, HEARN N, AKTAN H M. Active and non-active porosity in concrete Part I: experimental evidence[J]. Materials and Structures, 2002, 35(2): 110-116. DOI:10.1007/BF02482110 |
| [4] |
王海龙, 李庆斌. 孔隙水对湿态混凝土抗压强度的影响[J]. 工程力学, 2006, 23(10): 141-144. ( WANG Hailong, LI Qingbin. Effect of pore water on the compressive strength of wet concrete[J]. Engineering Mechanics, 2006, 23(10): 141-144. DOI:10.3969/j.issn.1000-4750.2006.10.027 (in Chinese)) |
| [5] |
杜修力, 金浏. 细观均匀化方法预测非饱和混凝土宏观力学性质[J]. 水利学报, 2013, 44(11): 1317-1325. ( DU Xiuli, JIN Liu. Micro-scale homogenization for prediction of the macroscopic mechanical properties of unsaturated concrete[J]. Journal of Hydraulic Engineering, 2013, 44(11): 1317-1325. (in Chinese)) |
| [6] |
李宗利, 杜守来. 高渗透孔隙水压对混凝土力学性能的影响实验研究[J]. 工程力学, 2011, 28(11): 72-77. ( LI Zongli, DU Shoulai. Experimental study on mechanical properties of concrete due to high seepage pore water pressure[J]. Engineering Mechanics, 2011, 28(11): 72-77. (in Chinese)) |
| [7] |
张永亮, 朱大勇, 李永池, 等. 干燥和饱和混凝土动态力学特性及其机理[J]. 爆炸与冲击, 2015, 35(6): 864-869. ( ZHANG Yongliang, ZHU Dayong, LI Yongchi, et al. Dynamic mechanical properties of dry and saturated concretes and their mechanism[J]. Explosion and Shock Waves, 2015, 35(6): 864-869. DOI:10.11883/1001-1455(2015)06-0864-07 (in Chinese)) |
| [8] |
彭刚, 王乾峰, 梁春华. 有压孔隙水环境中的混凝土动态抗压性能研究[J]. 土木工程学报, 2015, 48(1): 11-18. ( PENG Gang, WANG Qianfeng, LIANG Chunhua. Study on dynamic compressive properties of concrete under pore water pressure environment[J]. China Civil Engineering Journal, 2015, 48(1): 11-18. (in Chinese)) |
| [9] |
刘博文, 彭刚, 邹三兵, 等. 循环孔隙水作用下混凝土动态特性试验研究[J]. 土木建筑与环境工程, 2015, 37(5): 88-93. ( LIU Bowen, PENG Gang, ZOU Sanbin, et al. Experimental analysis of dynamic properties of concrete under cyclic pore water effects[J]. Journal of Civil, Architectural & Environmental Engineering, 2015, 37(5): 88-93. (in Chinese)) |
| [10] |
黄常玲, 刘长武, 高云瑞, 等. 孔隙水压力条件下混凝土的破坏机理[J]. 四川大学学报(工程科学版), 2015, 47(2): 76-80. ( HUANG Changling, LIU Changwu, GAO Yunrui, et al. Failure mechanism of concrete under pore water pressure[J]. Journal of Sichuan University: Engineering Science Edition, 2015, 47(2): 76-80. (in Chinese)) |
| [11] |
白卫峰, 解伟, 管俊峰, 等. 复杂应力状态下孔隙水压力对混凝土抗压强度的影响[J]. 建筑材料学报, 2015, 18(1): 24-30. ( BAI Weifeng, XIE Wei, GUAN Junfeng, et al. Influence of pore water pressure on compressive strength of concrete under complicated stress states[J]. Journal of Building Materials, 2015, 18(1): 24-30. (in Chinese)) |
| [12] |
CHEN Zhangfusheng, HU Yu, LI Qingbin, et al. Behavior of concrete in water subjected to dynamic triaxial compression[J]. Journal of Engineering Mechanics, 2010, 136(3): 379-389. DOI:10.1061/(ASCE)0733-9399(2010)136:3(379) |
| [13] |
王春来, 徐必根, 李庶林, 等. 单轴受压状态下钢纤维混凝土损伤本构模型研究[J]. 岩土力学, 2006, 27(1): 151-154. ( WANG Chunlai, XU Bigen, LI Shulin, et al. Study on a constitutive model of SFRC under uniaxial compression[J]. Rock and Soil Mechanics, 2006, 27(1): 151-154. (in Chinese)) |
| [14] |
梁辉, 邹荣华, 彭刚, 等. 基于Weibull统计理论的混凝土率型损伤本构模型研究[J]. 长江科学院院报, 2016, 33(2): 111-114. ( LIANG Hui, ZOU Ronghua, PENG Gang, et al. Rate-dependent constitutive model of concrete based on the statistical theory of weibull[J]. Journal of Yangtze River Scientific Research Institute, 2016, 33(2): 111-114. DOI:10.11988/ckyyb.20140695 (in Chinese)) |
| [15] |
彭刚, 刘德富, 戴会超. 钢纤维混凝土动态压缩性能及全曲线模型研究[J]. 工程力学, 2009, 26(2): 142-147. ( PENG Gang, LIU Defu, DAI Huichao. Investigation of dynamic constitutive model of steel fiber concrete under conventional tri-axial compression[J]. Engineering Mechanics, 2009, 26(2): 142-147. (in Chinese)) |
| [16] |
LEMAITRE J. Local approach of fracture[J]. Engineering Fracture Mechanics, 1986, 25(5/6): 523-537. |
 2017
2017 
